2.1 강도-부하 이론과 신뢰도 지수

금속배관의 신뢰도 평가는 다음과 같이 3단계로 크게 이루어진다(Bazan and Beck 2013, Caleyo et al. 2002, Hasan et al. 2012). 첫째, 배관의 고장을 정의하는 한계상태함수를 결정한다. 보통은 배관의 내부 운영압력이 파열압력 또는 잔류강도를 초과할 때 고장이 발생한다고 가정하고 한계상태함수를 정의하는 것이 일반적이다. 둘째, 배관의 파열압력을 계산한다. 하지만 이를 정확하게 산출하는 것은 매우 어렵기 때문에 파이프의 두께, 직경, 재질 등 기술적 변수와 부식결함의 크기를 고려하여 근사값을 구할 수 있는 계산모델을 이용한다. 배관공학 분야에서 널리 사용되는 계산모델로는 ASME, DNV-99, Battelle, PCORRC 등이 있다. 그리고 셋째는 신뢰도 지수(Reliability Index)를 도출하는 단계이다. 신뢰도 지수란 한계상태함수의 기댓값을 표준편차로 나눈 것으로 정의되며 한계상태함수를 구성하는 개별 변수에 대해 확률분포를 가정하여 유도한다. 신뢰도 지수가 얻어지면 표준정규분포를 이용하여 고장확률 또는 신뢰도를 계산할 수 있다. 하지만 신뢰도 지수를 수식으로 직접 유도하는 것은 거의 불가능하기 때문에 근사해법 또는 시뮬레이션이 필요하다. 실무적으로는 First Order Second Moment(FOSM), First Order Reliability Method(FORM), Second Order Reliability Method(SORM) 등과 같은 근사해법이 많이 이용되고 있다. 이와 같은 평가방법을 신뢰도기반 한계상태법(Reliability-Based Limit State Method)이라 부르며 배관시스템에 관한 ISO 표준에서도 이를 채택하고 있다.

먼저, 강도-부하 이론에 의한 신뢰도 지수의 유도과정에 대해 설명한다. 신뢰도 분야에서 고장이란 결함이 허용한계를 벗어난 사건으로 정의한다(Seo et al. 2010). 가스배관의 고장은 구간내 임의의 한 지점에서 운용압력이 배관파열압력을 초과할 때 발생하는 것으로 정의되므로 고장확률(Probability of Failure, POF)은 다음 식으로 나타낼 수 있다(Caleyo et al. 2002, Hasan et al. 2012).

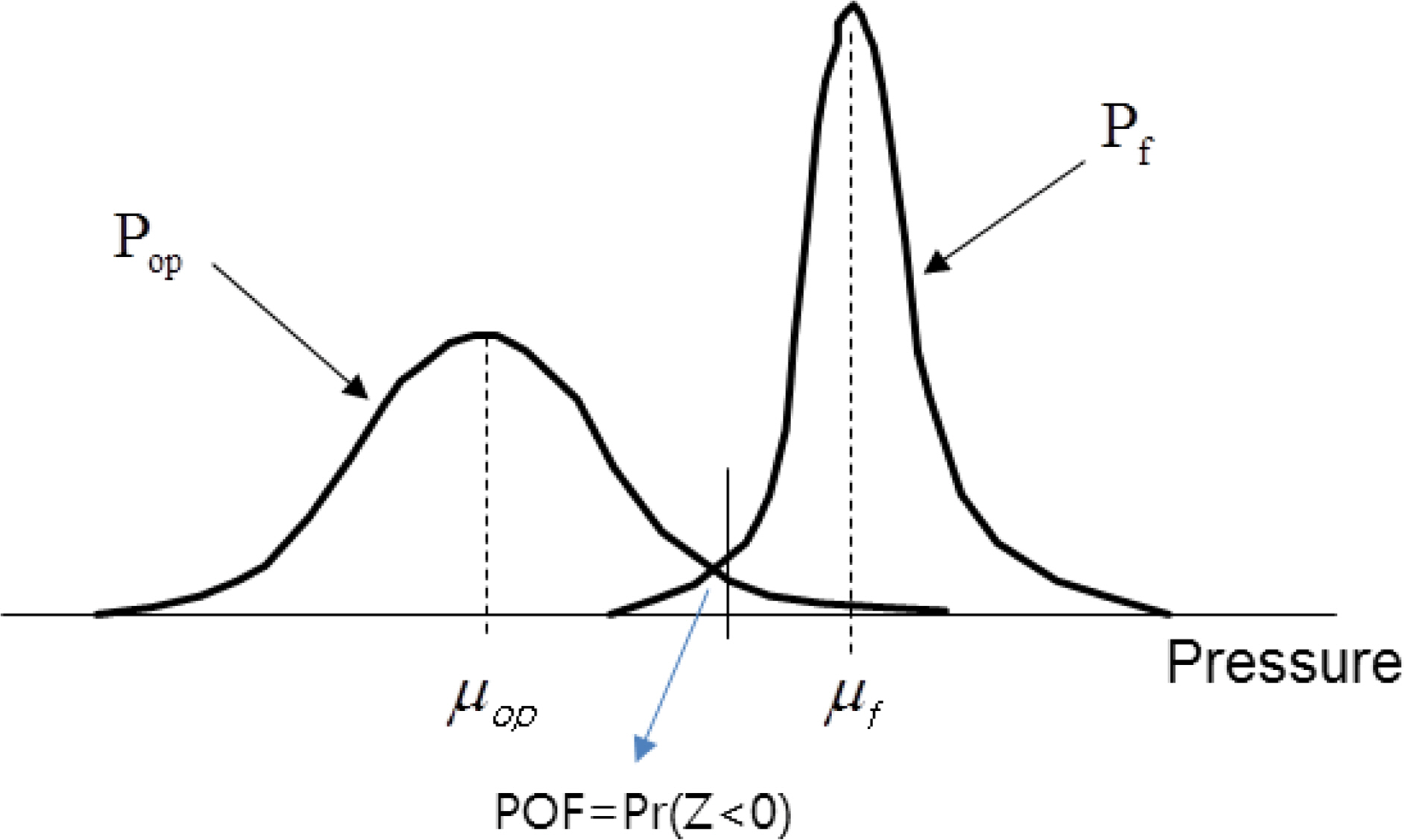
식 (1)에서 P_f와 P_op는 배관파열압력과 운용압력을 각각 의미한다. 여기서 P_f와 P_op가 정규분포를 따르는 확률변수라고 가정하고 그 평균과 표준편차를 각각 μ_f, μ_op그리고 σ_f, σ_op라 놓고 Z = P_f-P_op라 하면 식 (1)의 상황은 그림 1과 같은 강도-부하 모델을 이용하여 묘사할 수 있다. 여기서 고장을 정의하는 함수 Z를 한계상태함수(Limit State Function, LSF)라고 부른다. 또한 식 (1)은 정규분포에 관한 통계적 이론을 이용하면 다음과 같이 다시 쓸 수 있다.

Figure 1.

Probability of failure illustrated using strength-stress model

단 Φ(∙)는 표준정규분포의 분포함수이다. 또한 아래 식으로 표현되는 β는 구조신뢰도 분야에서 신뢰도 지수(Reliability Index)라고 부른다.

신뢰도 지수 β가 클수록 신뢰도가 높고 고장확률이 낮다. 예를 들어 β가 5 이상이면 고장확률은 1.0e-7 수준으로 얻어진다. 한편 고장확률은 P_f와 P_op의 표준편차 즉 σ_f와 σ_op에 의해서 큰 영향을 받게 되는 데 배관설계 분야에서는 파라미터 변동을 나타낼 때 표준편차보다 변동계수(Coefficient of Variation, CV)를 이용하는 경우가 많다. 변동계수란 표준편차를 평균으로 나눈 것으로 정의되며 이는 평균에 대한 변동의 상대적인 크기로 이해할 수 있다. P_f와 P_op의 변동계수를 δ_f와 δ_op라고 하면 각각 σ_f = μ_f δ_f와 σ_op = μ_op δ_op이므로 식 (3)은 다음과 같이 나타낼 수 있다.

다음 그림은 식 (4)를 이용하여 변동계수에 따른 고장확률의 변화를 보여주고 있다. 예시의 편의를 위해 평균은 각각 μ_f = 13.50, μ_op = 6.75로 하였다. 즉 변동계수가 커짐에 따라 고장확률이 증가하는 경향이 있음을 알 수 있고, 극단적이긴 하지만 변동계수를 0으로 설정하면 고장확률도 0이 된다. 또한 P_f의 변동계수가 P_op의 변동계수보다 고장확률에 영향이 더 크다는 사실도 알 수 있다.

Figure 2.

Probability of failure and coefficients of variations

하지만 식 (2)의 고장확률을 구하는 것은 간단하지 않다. P_f와 P_op는 매우 다양한 요인의 영향을 받을 뿐 아니라 또 다양한 확률분포를 따를 수 있기 때문이다. 실제로 P_f는 배관의 직경, 두께, 강도 등에 따라 그 값이 다르며 특히 부식과 같은 결함이 발생했을 때에는 더욱 복잡하게 변화할 수 있다. 앞서 언급한 바와 같이, 이러한 상황을 고려하여 P_f의 값을 근사적으로 얻을 수 있도록 다양한 계산모델이 개발되어 왔다.

Caleyo et al. (2002)는 모델 간의 차이와 특성에 대한 수치실험 결과를 제시하고 있으므로 상세한 내용을 참고하기 바란다. 본 논문은 이 중에서 PCORRC 모델을 대상에서 한다. 이 모델은 계산식이 비교적 간단하며 한국가스공사에서 개발된 KOPAP 모델과도 가장 유사하다는 특징이 있다. PCORRC 모델에 따르면 파열압력 계산식은 아래와 같이 주어진다.

식 (5)에서 UTS, w, D는 배관의 인장강도, 두께, 직경을 각각 의미하며 d(t)는 t년이 경과된 후의 부식깊이를 나타낸다. 또한 M은 다음과 같이 계산된다.

여기서 L(t)는 t이 경과한 후의 부식길이를 뜻하고 식 (6)을 살펴보면 d(t)가 w에 가까워지면서 P_f는 0으로 접근함을 알 수 있다.

2.2 신뢰도 계산을 위한 근사해법

먼저 P_f와 P_op를 편의상 x₁과 x₂로 각각 놓고 한계상태함수를 Z = g(x₁,x₂)라 하면 식 (2)의 고장확률은 다음과 같이 나타낼 수 있다.

식 (7)에서 f(x₁,x₂)는 x₁과 x₂의 결합확률밀도함수를 나타낸다. 하지만 이처럼 적분을 통해 고장확률을 구하는 것은 대부분의 경우 거의 불가능하다. 확률밀도함수는 대부분 알려져 있지 않거니와 설령 알고 있다고 하더라도 적분을 하기에는 그 형태가 매우 복잡하기 때문이다. 이러한 문제점을 극복하기 위해 First Order Second Moment(FOSM), First Order Reliability Method(FORM), Second Order Reliability Method(SORM) 등과 같은 근사적인 해법이 제안되어 왔다(Melchers and Beck 2018).

FOSM은 한계상태함수를 테일러전개를 통해 1차식으로 근사화하고 1차 및 2차 모멘트를 얻어서 고장확률을 계산하는 방식이다. 우선 한계상태함수에 포함되는 랜덤벡터를 X = (x₁,x₂,...,x_k)로 정의한다. 랜덤벡터를 구성하는 k개의 확률변수는 이미 전술한 파이프직경, 두께, 인장강도, 부식깊이, 부식길이 등을 의미한다. 한편 랜덤벡터 X의 기댓값과 표준편차는 각각 μ = (μ₁,μ₂,...μ_k)와 σ = (σ₁,σ₂,...,σ_k)로 나타내기로 한다. 그러면 테일러전개를 적용하여 한계상태함수는 다음과 같이 나타낼 수 있다.

식 (8)에 대해 기댓값과 분산을 취하면 각각의 근사치를 다음 식 (9)와 (10)으로 구할 수 있다.

여기서 식 (10)의 결과는 k개의 확률변수가 서로 독립이라는 가정 하에 성립함을 유의하기 바란다. 식 (9)와 (10)을 식 (2)에 대입하면 다음과 같이 고장확률을 근사적으로 구할 수 있다.

물론 이 결과는 최종적으로 정규분포를 가정한 것이지만 정당화되는 경우가 많고 고장확률 근사치를 신속하게 얻을 수 있다는 점에서 이득이 있다.

FORM은 FOSM과 거의 동일한 방법이지만 Most Probable Point(MPP)를 이용함으로써 근사오차를 줄이고자 한 것이 특징으로 식 (8)에 μ 대신 MPP인 m^*를 대입하기만 하면 된다.

따라서 FORM에서는 MPP를 어떻게 정하느냐가 관건이 되지만 일단 식 (12)의 한계상태함수에 대해 기댓값과 분산을 취하면 다음과 같은 결과를 얻을 수 있다.

FOSM과 마찬가지로 식 (14)는 k개의 확률변수가 서로 독립이라는 전제 하에 얻어진 결과이다. 식 (13)과 (14)로부터 신뢰도지수를 β = μ^*_g/σ^*_g와 같이 구하고 식 (2)에 대입하면 FORM의 고장확률을 계산할 수 있다. MPP를 탐색하는 알고리즘에 대해서는 Melchers and Beck(2018)을 참고하기 바란다. 한편 SORM은 근사오차를 더욱 줄이기 위해 한계상태함수를 다음과 같이 2차항까지 근사화시키는 기법이다.

식 (15)에서 H(m^*)는 MPP에서의 g(X)의 Hessian Matrix이다. SORM은 근사오차를 줄이는 데 도움이 되지만 H(m^*) 계산 등 복잡한 절차가 필요하다. 따라서 실무적으로 FOSM이나 FORM이 선호되고 있으며 특히 계산과정이 간단한 FOSM이 가장 널리 이용되고 있다. 본 논문에서도 고장확률 계산에 FOSM 알고리즘을 적용한다. FOSM은 몬테카를로 시뮬레이션 결과와 비교적 일관성이 있고 오차도 일정 범위 내에 있음이 보고된 바 있다(Hasan et al. 2012).

3.1 고장유형과 한계상태함수

전술한 바와 같이, 배관 사용연수가 증가함에 따라 부식에 의한 고장이 차지하는 비중은 커지게 된다. 부식은 시간이 경과함에 따라 확산되기 때문이다. 부식은 배관의 내압강도를 약화시키고 다양한 형태의 고장을 일으킬 수 있다. Canadian Standard Association에 따르면, 부식을 원인으로 하는 배관고장은 다음 그림과 같이 Small Leak, Large Leak, Rupture로 구분될 수 있다. 이 분류는 파이프 표면에 식별된 부식결함의 깊이와 길이에 따른 것이다.

Figure 3.

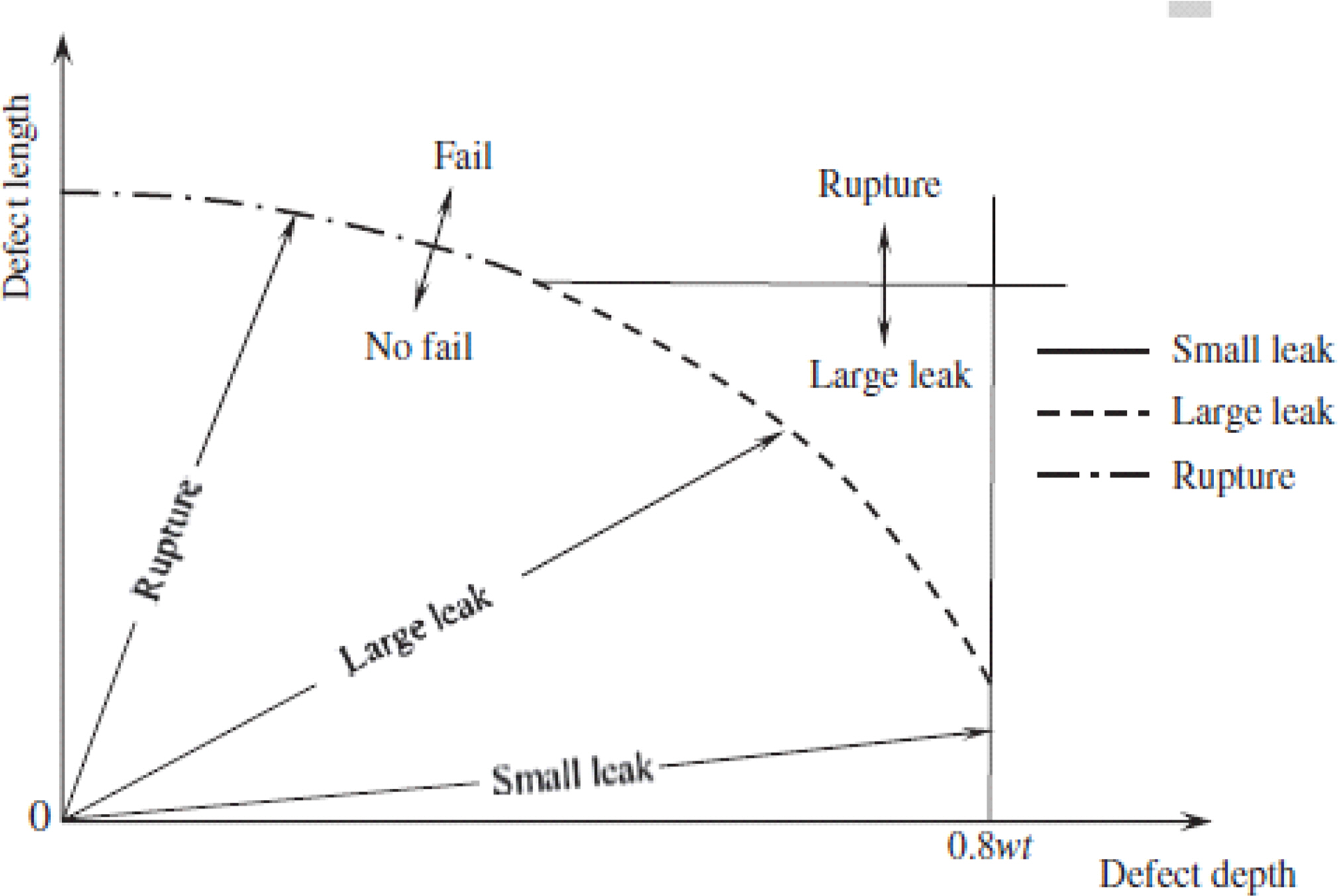
Failure modes based upon corrosion defect size (Zhang et al. 2019)

즉 Small Leak는 부식길이 L은 매우 짧지만 부식깊이 d가 큰 경우로서 핀홀 형태의 부식결함으로 인해 가스가 누설되는 고장을 말한다. Large Leak는 국부적인 부식결함으로 인해 배관의 잔류강도가 약화되면서 가스가 누설되는 고장이고, Rupture는 파이프 전역에서 부식이 광범위하게 진행되어 심각한 중량손실이 발생하면서 가스가 누설되는 고장을 뜻한다. 이와 유사하게, Zhang et al.(2019)는 부식결함을 아래 그림과 같이 Pitting Corrosion, Local Corrosion, Uniform Corrosion의 3단계로 구분하고 고장유형이 서로 종속적일 수 있으므로 고장확률을 개별적으로 평가하기 보다는 이들을 동시에 고려한 복합고장확률을 다루는 것이 더 현실적이라는 의견을 제시하였다.

Figure 4.

Failure modes due to corrosion

Pitting Corrosion은 대단히 국부적이고 중량손실이 거의 없으므로 큰 어려움을 야기하지는 않지만 부식깊이가 한계를 넘어설 경우에는 Small Leak가 발생하게 된다. 그러므로 시점 t에서 Small Leak 발생에 대한 한계상태함수는 다음 식과 같이 나타낼 수 있다(Gomes et al. 2013, Zhang et al. 2019).

식에서 w는 Wall thickness를 나타내므로 부식깊이가 파이프 두께의 80%에 이르면 고장이라는 의미이다. 다음, Local Corrosion으로 인해 주로 발생하는 Local Burst는 아래의 한계상태함수로 나타낼 수 있다.

Local Burst는 배관고장의 가장 일반적인 유형이라고 할 수 있으며 앞의 2.1절에서도 식 (18)을 기준으로 설명을 전개한 이유이다. 따라서 P_f(t)는 시점 t에서의 파열압력을 PCORRC 모델로 계산한 것에 해당된다. 마지막으로, Uniform Corrosion은 Rupture 고장을 일으킬 수 있으므로 이에 대한 한계상태함수는 아래와 같다.

단 P_rup(t)는 시간 t에서의 Rupture 압력을 의미하며 계산모델에서 제공하는 산식으로 그 값을 얻을 수 있다.

3.2 Small Leak와 Burst를 고려한 복합고장확률

앞의 식 (17), (18), (19)과 같은 한계상태함수를 이용하면 Small Leak, Local Burst, Rupture에 해당되는 고장확률 POF_sl, POF_local, POF_rup을 각각 다음 식으로 나타낼 수 있다(Zhang et al. 2019).

고장확률을 개별적으로 다루기 보다는 고장유형이 확률적으로 중첩될 수 있음을 다루기 위해 본 논문에서는 복합고장확률(Probability of Composite Failure, PCF)을 다음과 같이 정의한다.

여기서 다변량 정규분포(Multivariate Normal Distribution)를 가정하면 PCF의 계산식을 얻을 수 있다. 우선 k개의 확률변수로 구성되는 랜덤벡터 y= (y₁,y₂,...,y_k)에 대한 다변량 정규분포의 확률밀도함수는 다음과 같다.

식 (22)에서 μ = (μ₁,μ₂,...,μ_k)이고 ∑는 랜덤벡터 y의 공분산행렬을 의미한다. 단 k = 2일 경우는 공분산행렬은 아래와 같이 나타낼 수 있다.

단 σ_ij = Cov(y_i,y_j) = ρ_ijσ_iσ_j이다. ρ_ij는 확률변수 y_i와 y_j의 상관계수로서 i = j이면 ρ_ij = 1이 된다. 그리고 σ_i와 σ_j는 확률변수 y_i와 y_j의 표준편차를 각각 나타낸다. 즉 이변량 정규분포 하에서 PCF는 다음과 같이 표현된다.

단 ρ₁₂ = ρ₂₁ = ρ로 놓았고, β₁과 β₂는 한계상태함수 g₁과 g₂에 대해 얻어진 신뢰도 지수를 각각 나타낸다. 여기서 ρ = 0이라고 가정하면 PCF는 다음과 같이 간단하게 얻어진다.

즉 POF₁ = Pr(g₁ ≦ 0) = Φ(- β₁)와 POF₂ = Pr(g₂ ≦ 0) = Φ(- β₂)가 주어지면 PCF를 바로 구할 수가 있다. 여기서 β₂는 2장에서 기술한 FOSM을 이용하여 계산할 수 있고, β₁은 훨씬 더 간단하게 아래에 설명할 관계식으로 구할 수 있다. 먼저, 간단한 표현을 위해 한계상태함수 (17)을 g₁ = kw - d로 놓으면 기댓값을 다음과 같이 구할 수 있다. 단 k = 0.8이었다.

여기서 확률변수 w와 d가 서로 독립이라고 하면 g₁의 분산은 다음과 같이 표현된다.

단 δ_t와 δ_d는 각각 t와 d의 변동계수를 나타낸다. 따라서 식 (26)과 (27)을 이용하면 신뢰도지수 β₁은 다음과 같이 얻을 수 있다.

또한 부식깊이 비율을 f = μ_d/μ_w과 같이 놓으면 식 (28)은 다음과 같이 나타낼 수 있다.

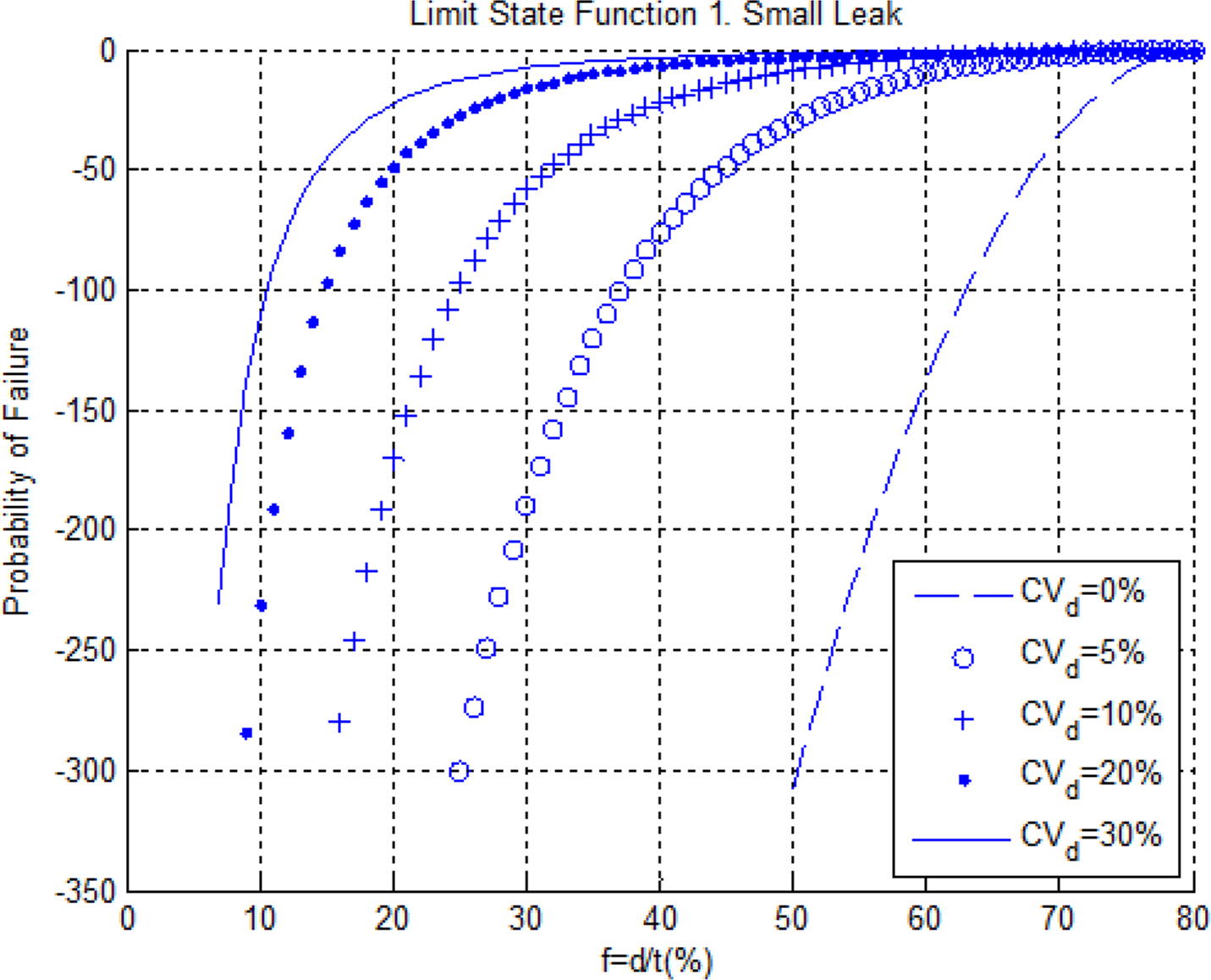
이제 깊이 방향으로의 부식진행률 f와 변동계수 δ_d에 따라 POF₁ = Φ(- β₁)가 어떻게 변화하는지 그래프로 나타낸다. 아래 그림에 나타나 있듯이, 부식진행률 f가 증가함에 따라 고장확률은 매우 빠르게 증가하는 모습을 보인다. 또한 부식깊이 변동계수 δ_d가 10%를 초과하면 POF₁ 역시 1로 빠르게 접근하고 있다. 따라서 δ_d를 적절하게 설정하는 것은 고장확률 및 잔여수명 예측에 중요한 역할을 차지함을 알 수 있다. 그림에서 파이프 두께의 변동계수는 배관사양을 참고하여 δ_w = 0.01로 고정시켰다.

Figure 5.

Probability of small leak failure with and corrosion rate and coefficient of variation

3.3 수치예제

예제 데이터를 이용하여 복합고장확률 계산결과를 살펴보고자 한다. 부식결함 데이터의 확보는 흔히 피깅(Pigging)이라 불리우는 In-line inspection을 통해 이루어진다. 이는 배관매설 후 일정 기간이 경과하면 가스배관의 상태를 점검하기 위해 실시되는 작업으로 부식결함의 위치, 형상, 크기 등과 같은 데이터를 얻을 수 있다. 피깅은 크게 Magnetic Flux Leakage(MFL)와 Ultrasonic 두 가지 방식으로 나누어진다. Ultrasonic 방식이 측정오차가 작아 정밀한 조사가 가능하지만 아직 상용화 단계에는 이르지 못하고 있어 대부분은 MFL 기반의 피깅에 의존하고 있다. 이 때 배관표면의 부식결함은 MFL 신호를 토대로 재구성되기 때문에 어느 정도의 측정 및 계산 오차를 감수해야 한다(Cosham et al. 2007).

한편 시간에 따른 고장확률의 변화를 고찰하려면 부식결함의 크기가 어떻게 성장하는지를 함께 연구해야 한다. 파열압력을 계산할 때 요구되는 부식결함의 깊이와 길이를 주어진 시점에서 예측, 제공해야 하기 때문이다. 여기에는 선형모형이 널리 이용되는 데 적용이 간단하고 많은 데이터를 필요로 하지 않는 장점이 있다. 하지만 부식성장을 과대추정하는 경향이 있기 때문에 멱함수나 확률과정 등을 이용한 대안도 검토되고 있다(Bazan and Beck 2013).

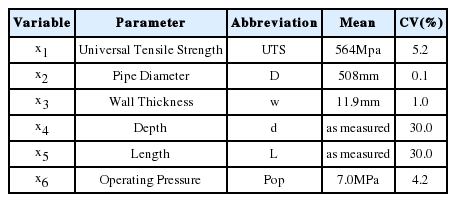
여기서 활용할 데이터는 예시를 위해 몇 차례 수정이 가해진 것으로 원래는 1993년 6월 서비스를 개시한 20인치 직경의 X65 강관을 대상으로 2014년 12월 20km 테스트 구간에서 피깅을 실시한 결과 얻어진 것이다(Kim et al. 2016). 수정 데이터는 총 75개의 가상적인 부식결함을 포함하고 있는 데 우선 FOSM 알고리즘을 적용하기 위해서는 주요 변수에 대해 평균과 변동계수를 사전에 설정해 주어야 한다. 본 예시를 위해 6개 변수에 대한 설정한 내용은 다음 표와 같다.

Table 1.

Parameter Setting for FOSM Algorithm

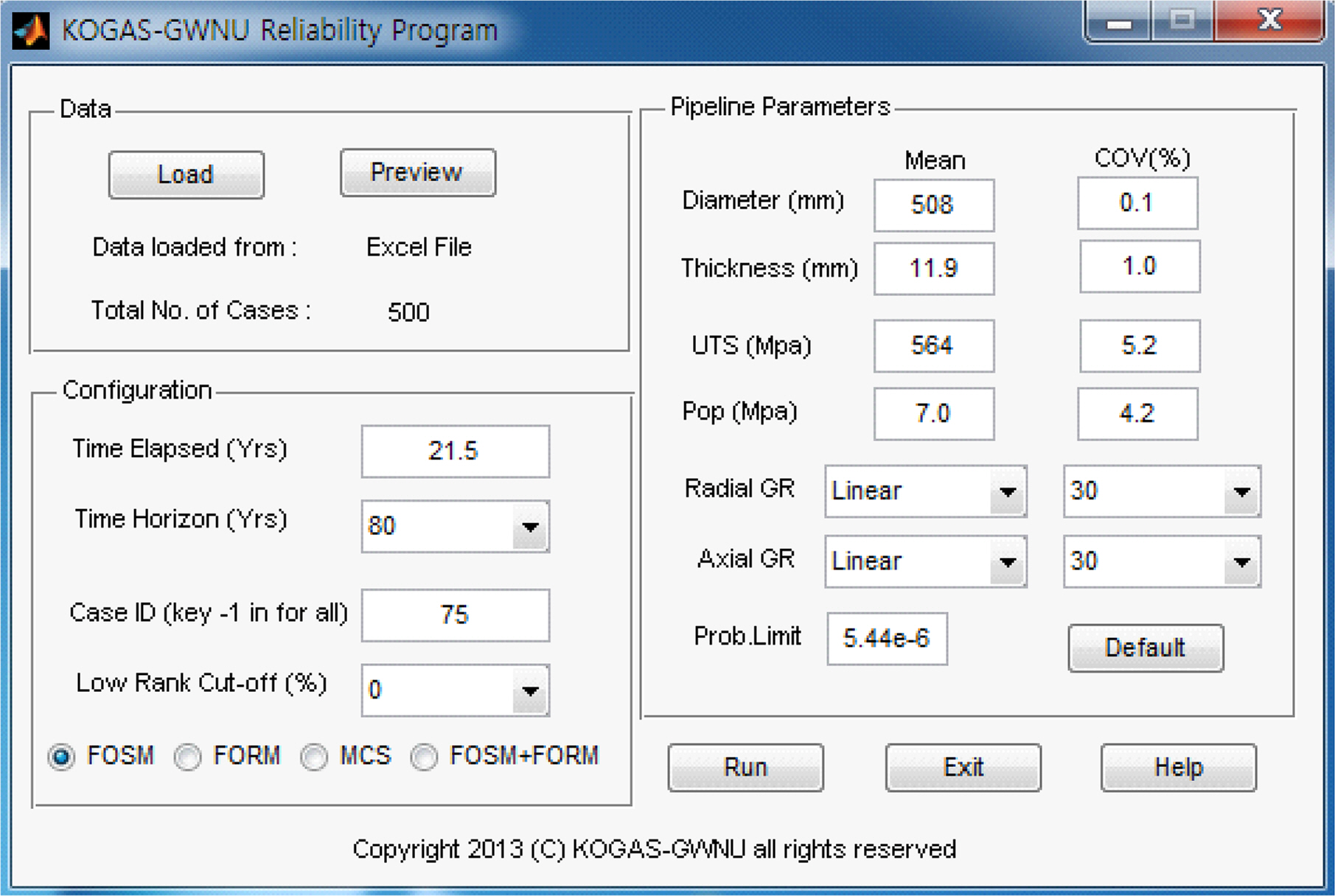
인장강도, 직경, 두께의 변동계수는 설계사양을 참고하였고, 부식깊이 및 부식길이에 대한 변동계수는 피깅 데이터셋의 예비 분석결과를 토대로 설정하였다. 또한 운영압력의 변동계수 4.2%는 내부 운영자료를 분석하여 도출한 값이다. 운영압력의 평균값은 당초 최대운영압력(Maximum Allowable Operating Pressure, MAOP) 7.0Mpa로 설정이 되었다. 하지만 이렇게 할 경우 고장확률이 지극히 작은 값이 되어 시간경과에 따른 변화가 제대로 나타나지 않았기 때문에 예시 차원에서 계산 프로그램 상에는 그 두 배인 14.0Mpa를 적용하였다. 한편 아래 그림은 FOSM을 적용하기 위해 상기의 설정값들을 기 개발된 MATLAB 프로그램에 입력하는 장면을 보여준다.

Figure 6.

Program interface for FOSM parameter setting

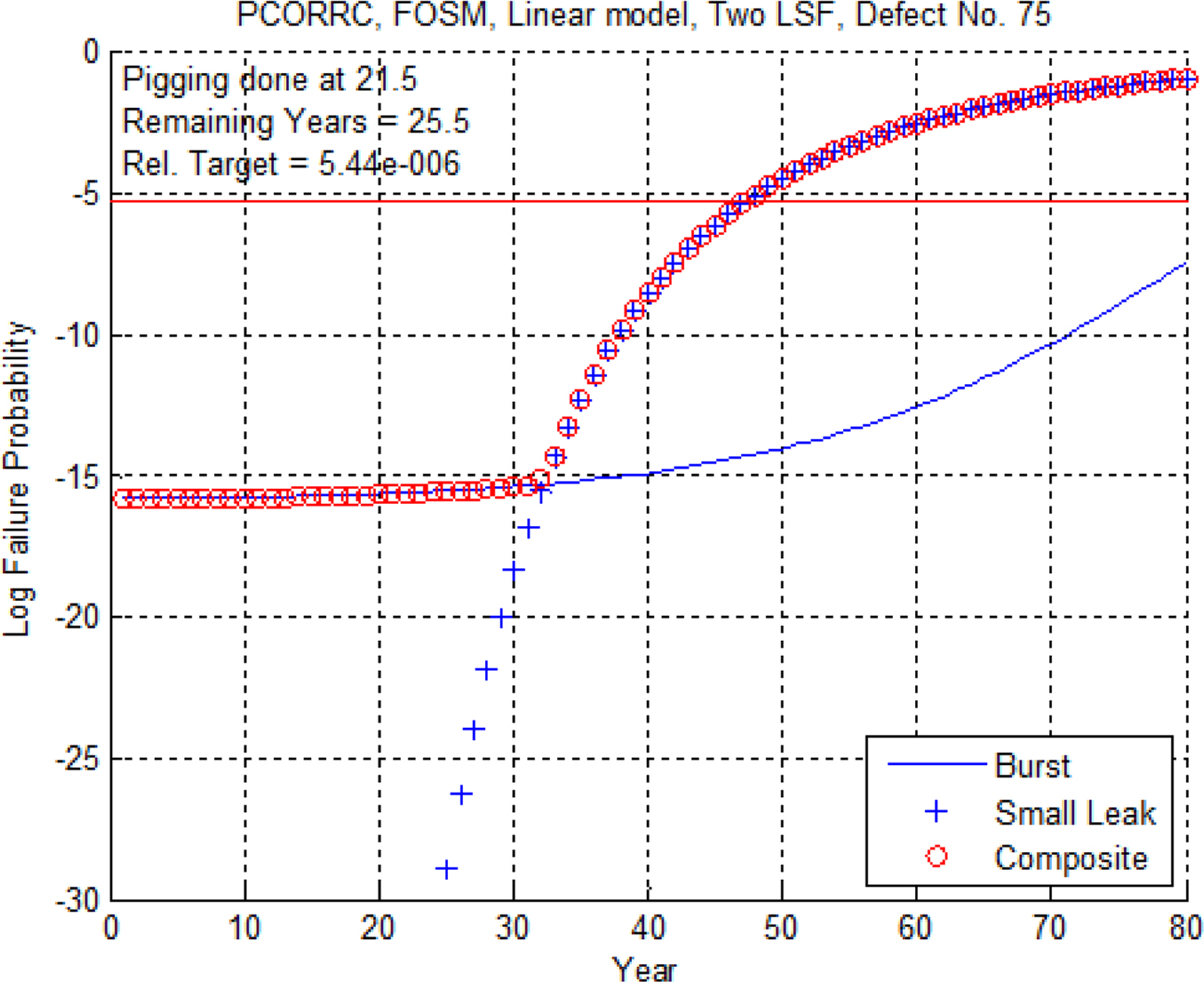
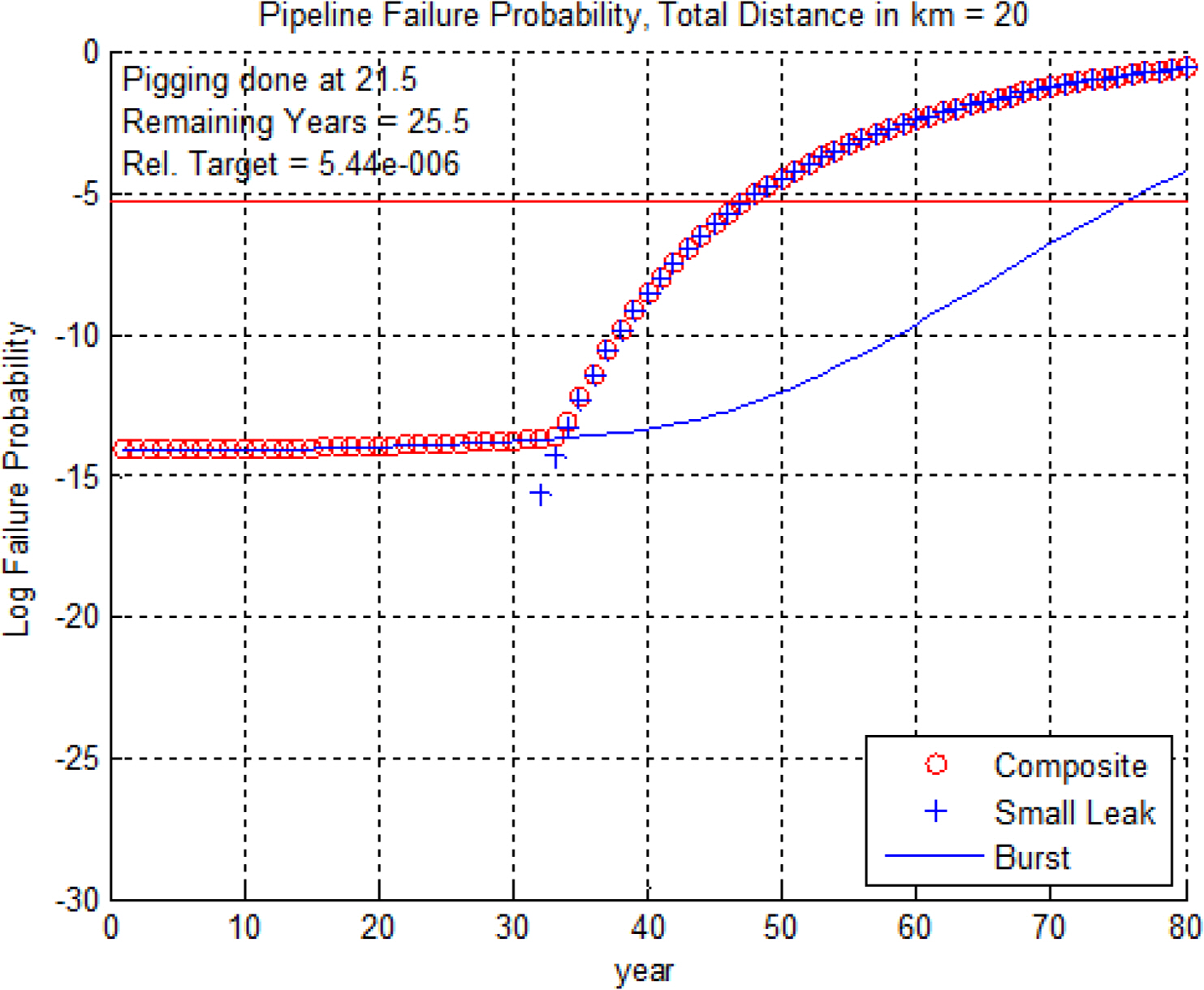
이제 복합고장확률 PCF가 어떤 모습을 보이는지 살펴보기로 하자. 비교를 위해 POF₁과 POF₂도 함께 그림에 나타내기로 한다. 시간에 따른 부식성장 예측치는 선형모형을 통해 제공하고, 파열압력은 PCORRC 계산모델을 이용하며 FOSM 알고리즘에 의한 계산결과를 도시한다. 우선 부식깊이가 가장 컸던 75번 결함에 대한 고장확률 계산결과는 다음 그림과 같다.

Figure 7.

Probability of composite failure - No. 75

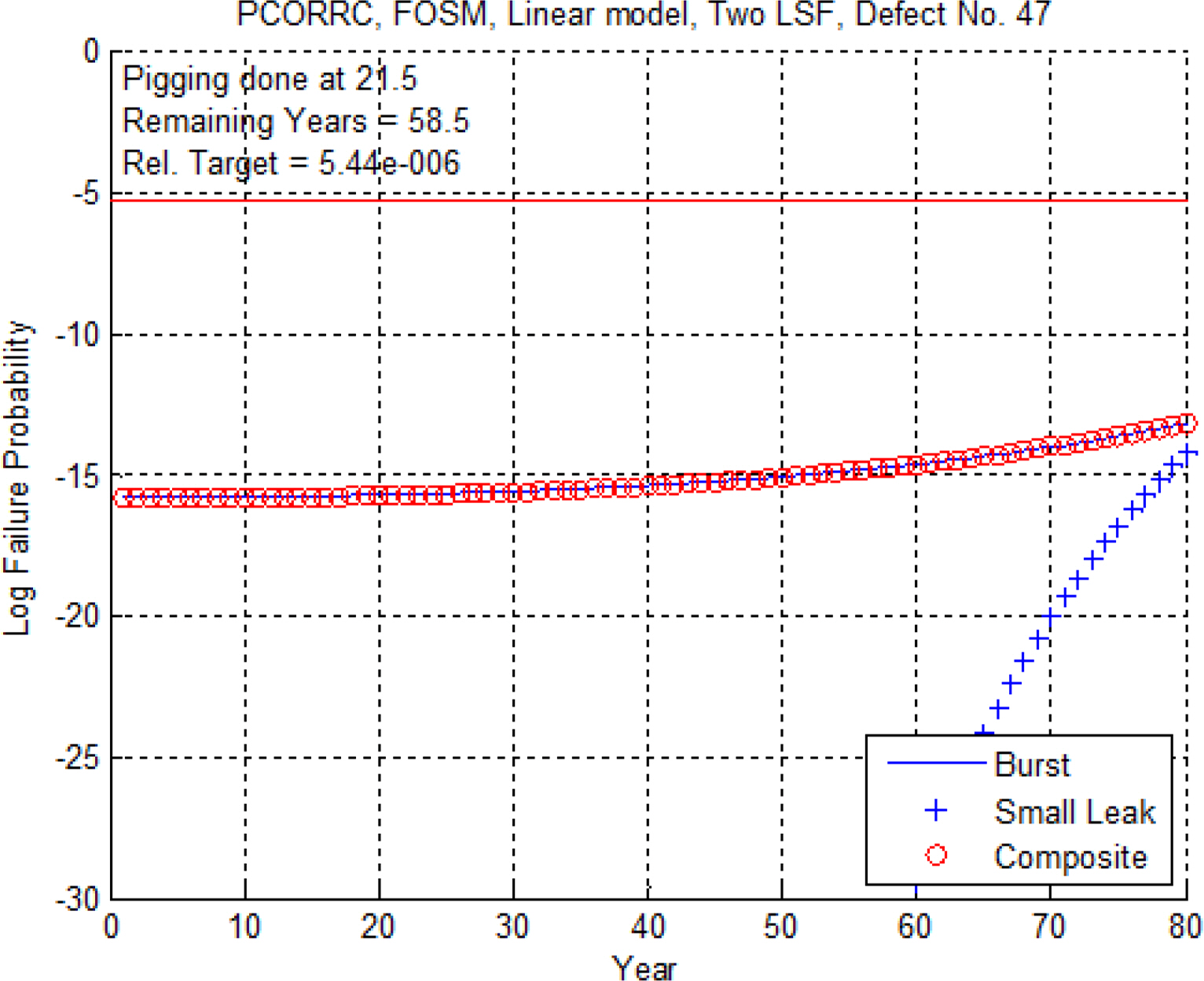
그림 7은 서비스가 개시된 1993년 6월부터 80년 동안의 고장확률을 잘 보여주고 있다. PCF는 47년째 되는 시점에 고장확률 한계치인 5.44e-6에 도달할 것으로 예상된다. 피깅이 이루어진 2014년 12월이 21.5년째에 해당되므로 잔여수명은 25.5년으로 예측할 수 있다. 이 결과는 POF₂ 만을 고려했을 때 예측되는 잔여수명과는 40여년 정도 차이가 있음을 알 수 있다. 다음 그림은 부식의 길이가 큰 결함 중 하나인 47번에 대한 고장확률 계산결과이다.

Figure 8.

Probability of composite failure - No. 47

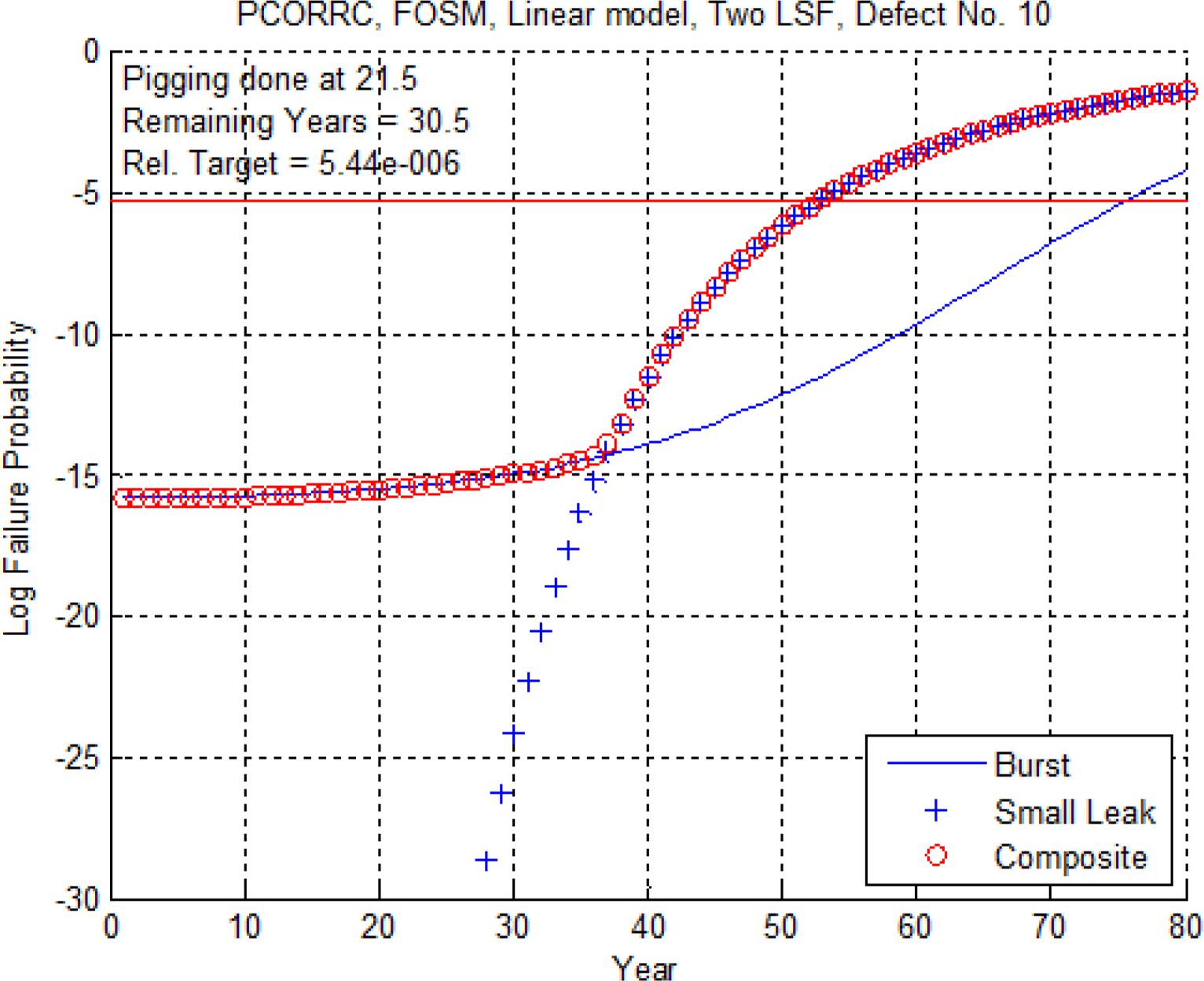
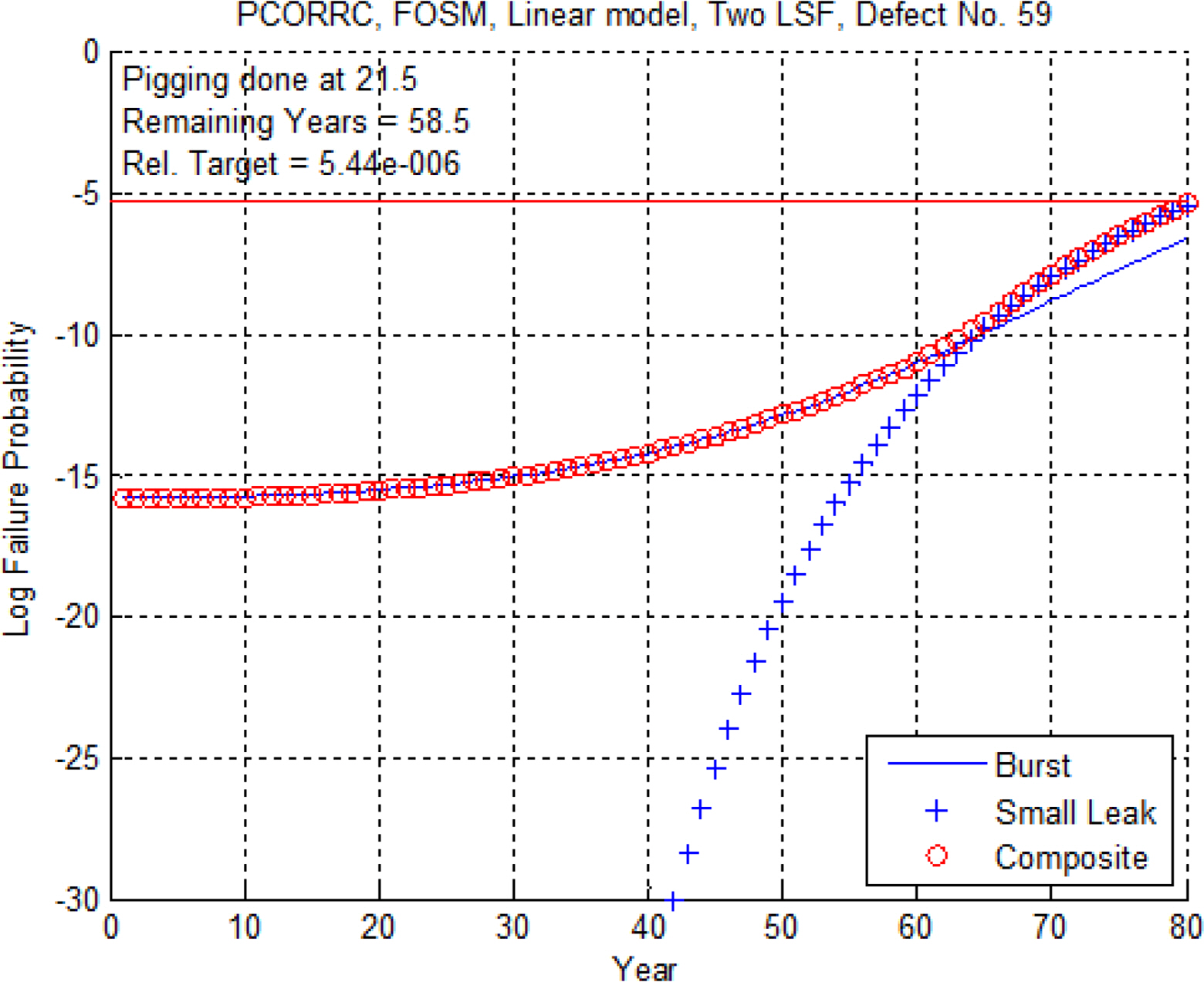
결함 47번은 부식길이는 큰 값이었던 반면 부식깊이가 매우 작은 경우였으므로 POF₁은 거의 0에 가깝게 나타나고 있다. POF₂ 역시 80년이 경과하기까지 매우 낮은 수준을 보이고 있으며 따라서 복합고장확률도 계속 미미한 값에 머물러 있음을 알 수 있다. 결함 47번에 대한 잔여수명은 매우 클 것으로 판단되지만, 프로그램 상으로는 매설 후 80년까지만 계산이 가능하기 때문에 여기서 피깅시점인 21.5년을 차감한 58.5년으로 잔여수명이 출력되고 있음을 유의하기 바란다. 아래의 그림 9와 10은 부식깊이와 부식길이 모두 비교적 값이 큰 결함 10번과 59번에 대한 결과이다. 결함 10번의 경우, 복합고장확률은 53년째 되는 해에 허용한계에 도달한다. 이 결과는 POF₂ 만을 고려했을 때보다 25년 정도 이른 것이다. 결함 59번도 역시 복합고장확률은 80년째 되는 해에 허용한계에 도달하고 있으므로 POF₂ 만을 따를 때에 비해 10년 정도 잔여수명이 단축되고 있음을 알 수 있다. 한편 부식깊이와 부식길이가 모두 비교적 작을 때에는 복합고장확률과 POF₂는 그리 큰 차이를 보이지 않는다. 이는 부식깊이가 작을 경우 더욱 두드러지는 데 그 이유는 Small Leak 고장확률이 거의 0에 가깝기 때문이다.

Figure 9.

Probability of composite failure - No. 10

Figure 10.

Probability of composite failure - No. 59

지금까지는 개별 결함에 대해 복합고장확률을 살펴보았다. 이 결과를 종합해서 테스트 구간 전체에 대해 복합고장확률을 구할 수 있다. 개별 결함마다로 얻어진 복합고장확률을 PCF_i라고 하면, 배관 전체의 복합고장확률은 총 n개의 결함 중 적어도 하나가 고장을 일으킬 확률이므로 다음 식으로 나타낼 수 있다.

단 n은 해당 구간에서 식별된 결함의 갯수이다. 아래 그림은 75개 결함 모두를 대상으로 한 배관 전체의 복합고장확률을 도시한 것으로 테스트 구간의 잔여수명은 25.5년으로서 예측되어진다. 이는 Burst 고장확률 만을 이용할 때에 비해 약 30년이나 앞당겨진 결과이다.

Figure 11.

Probability of composite failure on whole pipeline

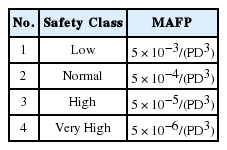
마지막으로, 본 예시에서 잔여수명을 구하는 기준으로 5.44×10e-6를 적용한 배경을 설명한다. ISO 16708:2006(E)는 가스배관의 신뢰성 평가를 위한 확률적 분석과 관리기준에 대한 글로벌스탠다드이다. 여기서는 배관매설 지역의 안전등급에 따라 허용될 수 있는 km당 고장확률의 한계인 MAFP(Maximum Allowable Failure Probability)를 아래 표와 같이 제시하고 있다. 단 Small Leak는 대상에서 제외하고 있으며 산식의 P와 D는 내부운영압력(bar)과 배관직경(m)을 각각 의미한다.

Table 2.

Maximum allowable failure probability according to the safety class

우리나라는 인구밀도가 높고 도시 주거지에 많은 배관이 매설되어 있는 관계로 대부분 4등급인 Very High에 해당될 것으로 판단된다. 표의 MAFP 산식에 P = 14.0Mpa = 140bar, D = 508mm = 0.508m를 대입하면 안전등급 4일 때의 최대허용한계는 MAFP = 5×10^-6/(140×0.508³)> = 2.72×10^-7과 같이 얻어진다. 여기에 테스트 구간의 길이인 20km를 곱하면 P_lim = 2.72×10^-7×20 = 5.44×10^-6으로 배관 전체에 대한 고장확률 한계를 구할 수 있다.