대안 부품을 고려한 다계층 시스템의 중복 할당을 위한 입자 군집 최적화
Particle Swarm Optimization for Redundancy Allocation of Multi-level System considering Alternative Units
Article information
Trans Abstract
Purpose
The problem of optimizing redundancy allocation in multi-level systems is considered when each item in a multi-level system has alternative items with the same function. The number of redundancy of multi-level system is allocated to maximize the reliability of the system under path set and cost limitation constraints.
Methods
Based on cost limitation and path set constraints, a mathematical model is established to maximize system reliability. Particle swarm optimization is employed for redundant allocation and verified by numerical experiments.
Results
Comparing the particle swarm optimization method and the memetic algorithm for the 3 and 4 level systems, the particle swarm optimization method showed better performance for solution quality and search time. Particularly, the particle swarm optimization showed much less than the memetic algorithm for variation of results.
Conclusion
The proposed particle swarm optimization considerably shortens the time to search for a feasible solution in MRAP with path set constraints. PS optimization is expected to reduce search time and propose the better solution for various problems related to MRAP.
1. 서 론
시스템을 설계할 때에는 시스템에 요구되는 성능을 비롯해서 고장의 발생 정도, 원자재 비용, 크기 등 다양한 측면에서 검토가 이루어진다. 그 중 신뢰도는 시스템 고장이 발생하였을 경우 치명적인 결과를 양산하는 시스템에 특히 중요하게 다뤄지게 된다. 신뢰도는 신뢰도가 높은 부품을 사용하거나, 유사한 기능을 가진 부품을 중복해서 사용함으로써 향상시킬 수 있다. 동일한 기능을 가진 부품은 다양하게 있으며, 어떤 부품을 사용하느냐에 따라 시스템의 신뢰도, 비용, 크기 등이 달라질 수 있다. 중복구조에 대한 중복할당 최적화 문제는 NP-hard 문제로 Fyffe et al.(1968) 이후로 다양한 문제와 최적화 방법에 대하여 연구가 되었다. 중복할당 문제에서 가장 기본적으로 다루어진 문제는 m개의 서브시스템을 가지는 시스템의 병렬-직렬 문제로 각 i번째 서브시스템에 중복 개수 ni를 결정하는 문제인데, 이 때 시스템의 개발 비용, 부피, 무게 등이 제약으로 사용된다(Chung, 2015).
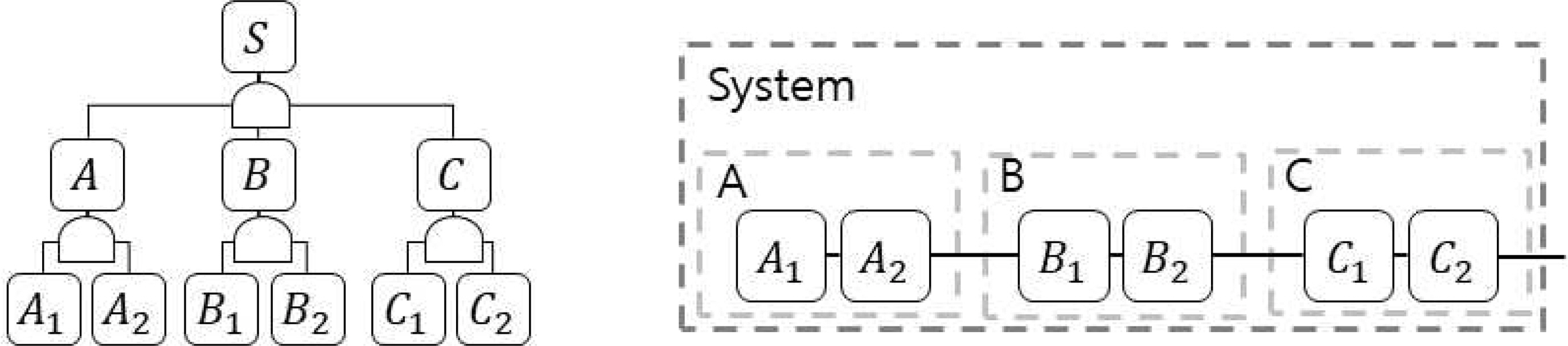
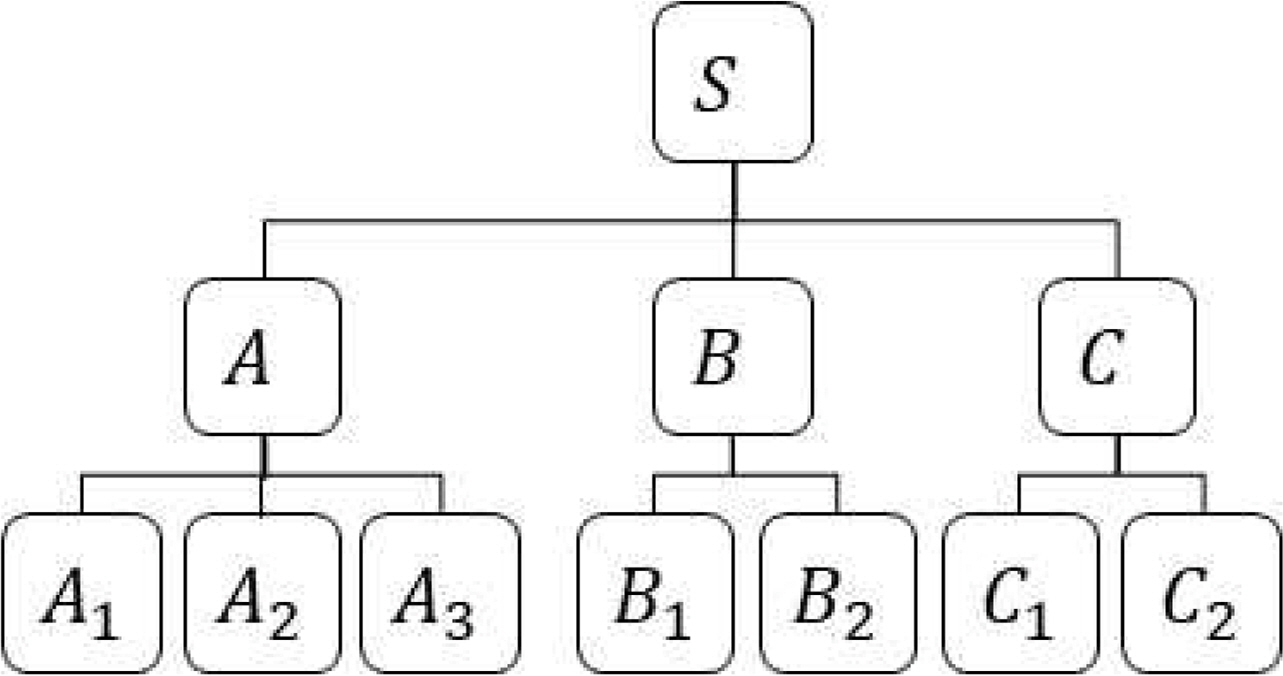
다계층 시스템은 부품들 간의 관계가 나무 형태로 상하 구분이 가능한 시스템을 나타낸다. 예를 들어, Figure 1의 시스템은 A, B, C 품목으로 구성이 되며, A는 A1, A2의 품목으로 구성되어 있음을 나타낸다.
Structure of multi-level system
다계층 시스템의 중복할당 문제는 경로집합에서 단 하나의 품목만 중복이 가능한 다수준 중복 할당 문제(MRAP; multi-level redundancy allocation problem)와 두 개 이상의 품목이 중복이 가능한 다중 다수준 중복 할당 문제(MMRAP; multiple multi-level redundancy allocation problem), 중복 품목에 대해 재중복이 가능한 다수준 중복 할당 최적화 문제(MRAOP; multi-level redundancy allocation optimization problem)로 나뉜다.
Yun and Kim(2004)은 다계층 시스템에 대해 MRAP를 처음 소개하였으며 경로집합에서 단 하나의 품목만 중복이 가능한 경우에 대해 유전알고리즘을 활용하여 최적화 방법을 제시하였다. 경로집합이란 최하위 수준의 하나의 품목에서 최상위시스템으로 이어지는 품목의 집합을 의미하며 Figure 1에서는 S-A-A1, S-A-A2, S-B-B1 등이 있다(Yun et al, 2017).
Kumar et al.(2008)은 MRAOP를 제시하였으며 계층적 유전 알고리즘, 미미틱 알고리즘, 박테리아 진화 알고리즘 등을 활용한 최적화 방법이 연구되었다(Yun et al, 2017). MRAP와 MMRAP, MRAOP의 문제는 각 품목이 한 가지 종류인 경우에 최적 중복 할당 방법을 나타내며, 동일한 기능을 가진 다양한 종류의 품목에 대한 선택은 고려하지 않고 있다. Chung(2015)은 MRAP에서 각 품목의 종류가 다양하게 존재할 경우 최적의 부품 선정과 중복 할당 수량을 다루었다. 최적화를 위해 유전 알고리즘과 미미틱 알고리즘을 활용하였으며, 이에 대한 비교 결과를 제시하였다. MRAP는 경로집합에서 단 하나의 중복만 허용함으로 인해 유효해를 찾는 과정이 복잡하고 어려우며, 이로 인해 탐색시간이 길어지는 단점을 가지고 있다. 본 연구에서는 대안부품을 가지는 MRAP에서 입자 군집 최적화(particle swarm optimization) 방법을 다루며 실험을 통해 미미틱 알고리즘과의 성능을 비교하고자 한다.
2. 대안부품을 가진 다계층 시스템 모형
단, 본 연구에서는 모든 품목이 중복 설계시 고려 대상이 되지만, 경로집합에서 단 한 개의 품목만이 중복 대상으로 선정되어지는 MRAP 모형을 기반으로 하고 있으며, 그 외 중복 설계 모형을 위한 가정 및 기호는 아래와 같다(Chung, 2015).
<가정>
(1) 각 품목들은 직렬로 연결되어 있다.
(2) 중복 품목 및 모든 품목들의 고장시간은 통계적으로 독립이다.
(3) 각 품목들의 신뢰도는 알려져 있고 확정적이다.
(4) 각 품목과 그 품목의 대안 품목들 중에 단지 하나의 품목만이 중복 가능하다.
(5) 경로집합에서 단 한 개 수준에 품목만이 중복 대상으로 선정될 수 있다.
위에서 언급한 ‘품목’은 시스템, 모듈, 부품을 나타내는 공통된 의미로 사용되며, 시스템은 최상위 품목, 부품은 최하위 품목, 모듈은 중간 수준 품목을 의미한다. 대안 부품을 고려하기 위해 Figure 1에서 A, B, ..., C1, C2등을 품목의 ‘군’으로 표현하며, 군에 사용 가능한 품목이 2종류 있는 경우
<기호 및 정의>
Rs : 전체 시스템 신뢰도
if : i 군의 경로 집합
mi : 위치 i에 대체 가능한 대안 부품들의 수
N : 품목 군의 수
lc : 최하위 품목 군의 집합
C(x : 중복할당 수를 고려하였을 경우 p군의 k번째 종으로 인한 소요 비용
CT : 시스템 비용한계
subject to
본 연구에서는 비용한계가 주어졌을 때 시스템 신뢰도를 최대화하는 문제로 식(1)은 다계층 시스템에 중복할당수가 결정되었을 때 시스템의 신뢰도를 계산하는 목적함수이며, 식(2)는 비용한계, 식(3)은 경로집합의 제약과 한 개의 군에서는 한 종의 품목만을 사용할 수 있다는 가정을 나타낸다.
3. 최적 중복할당을 위한 입자 군집 최적화
입자 군집 최적화는 자연에서 물고기, 새와 같은 군집 활동을 하는 행위에 착안하여 Kennedy and Eberhart(1995)에 의해 개발되었다. 유전알고리즘이나 개미알고리즘에서 중요한 개념으로 사용되는 교차, 돌연변이, 페르몬과 같은 연산을 수행하지 않으며, 입자들의 변화는 과거의 군집활동을 바탕으로 이루어진다.
xi와 vi는 i 번째 입자의 위치와 속도 벡터, ε1와 ε2는 0과 1사이 난수값, α와 β는 가중치, g*와
입자 군집 최적화 방법은 연속적 비선형 함수를 최적화 하는데 많이 활용 되어지고 있다. 본 연구에서 다루고자 하는 중복 할당 최적화는 각 품목의 종류와 중복 수량을 결정해야 하는 것으로 최적화의 변수가 양의 정수의 형태로 나타난다. 이러한 문제에 대해 Yeh(2009)는 Yun et al.(2007)이 제시한 MMRAP에 대해 이단계 이산 입자 군집 최적화 방법을 제시하였으며, Yeh et al.(2016)에서는 GMRAP(general multi-level redundancy allocation problem)을 소개하고 Yeh(2009)에서 제시한 방법을 활용하여 최적화 방법을 제시하였다. 본 연구에서는 대안 품목을 고려한 MRAP에서 이산 입자 군집 최적화를 위해 해의 표현, 해의 상한값, 해의 평가, 최적화 절차를 제시하고 최적화 절차에서 t+1세대에서의 i번째 입자의 위치와 속도 산출 방법은 Yeh(2009)가 제시한 방법을 인용하여 적용하고자 한다.
3.1 해의 표현
입자 군집 최적화 방법을 적용하기 위해서는 먼저 각 입자를 해의 형태로 표현을 해야 한다. 해의 표현은 경로제약에 따른 유효해 탐색과 다음 위치의 해를 탐색하는데 많은 영향을 주기 때문에 문제의 특성에 맞게 적절한 방법으로 표현해야 한다. 본 연구에서 해의 표현은 중복할당 수를 나타내는
3.2 상한값
각 입자에서 각 품목별 중복할당 수는 세대가 반복됨에 따라 변경되어진다. 품목별 중복할당 수의 가능한 범위를 예측할 수 있다면, 탐색 범위를 좁힐 수 있으며 이로 인해 탐색 시간을 줄일 수 있다. 중복할당 수와 관련된 제약은 비용에 대한 제약으로 식(2)와 연관되어져 있다. 이에 대해 Yeh(2009)는 최적화 과정에서 허용 가능한 총 비용을 사용해서 각 품목에 대한 중복할당 상한을 적용하고 있다. 본 연구에서는 한 개의 품목에 다양한 군이 존재하고 각 군의 비용이 다름으로 인해 각 품목 군에서 종의 중복 상한값은 최하위 품목이 중복을 가지지 않을 때 최소값을 산출한다. 따라서, k 품목군에 p종의 중복수량 상한값
3.2 초기 모집단
본 연구에서는 임의 생성 방법으로 초기해를 생성할 경우 제약식을 만족시키는 해를 만드는데, 상당한 시간이 소요됨으로 처음에는 최하위 품목 군에서 첫 번째 종을 사용하는 것으로 정한다. 또한, 각 품목 군의 첫 번째 종의 중복개수는 적용이 가능한 중복 수의 상한을 고려해서 임의로 생성한다.
3.3 해의 평가
비용 한계가 주어졌을 때 시스템 신뢰도를 최대로 하는 중복 최적화 문제에서 해의 평가는 각 해의 신뢰도로 주어질 수 있다. 각 해는 식(8)과 같이 시스템 신뢰도에서 벌금을 제하여 계산하고 있으며, 벌금은 각 해가 비용 한계를 초과하였을 경우 초과한 비용과 비용한계의 비율에 벌금함수 비율 α를 적용하여 산출하고 있다. 따라서, k 입자 vk에서 i군 품목의 j종의 중복 수가
3.4 이산 입자 군집 최적화
MRA에서 다음 세대의 입자를 결정하는데 있어 중복 대상 품목의 변경은 경로집합 제약으로 인해 유효하지 않은 입자를 생성할 수 있다. 유효하지 않는 입자는 임의적 위치 수정을 통해 유효 입자로 변경해야 하는 어려움과 이로 인해 많은 탐색 시간을 소요하게 된다. 본 연구에서는 경로 집합에 따라 유효하지 않는 입자가 발생하는 것을 방지하기 위해 중복 대상 품목과 수량을 결정할 때 항상 유효 입자를 유지 할 수 있도록 절차를 개발하여 제안한다. 해의 임의성을 향상시키기 위해 Step 1과 Step 2에서는 품목 군의 순서를 임의적으로 변경하여 중복대상 품목과 수량을 결정하며, Step 4에서는 경로집합의 제약에 따라 같은 군과 경로집합에 있는 품목의 중복할당 수량을 0으로 변경시키게 된다. 이렇게 모든 입자에 대해 Step 1~Step 5를 실시하여 t 세대의 입자를 구할 경우 모든 입자의 위치는 유효한 입자로 생성이 가능하게 된다.
Step 1 : 다음 세대의 위치를 결정하기 위해 입자 vi에서 품목 군의 순서를 임의적으로 변경한다. 단, 같은 군의 품목의 순서는 연속되게 한다. 예를 들어, vi는 다음과 같이 순서 변경이 될 수 있다.
Step 2 :
Step 3 : 0에서 1사이의 임의의
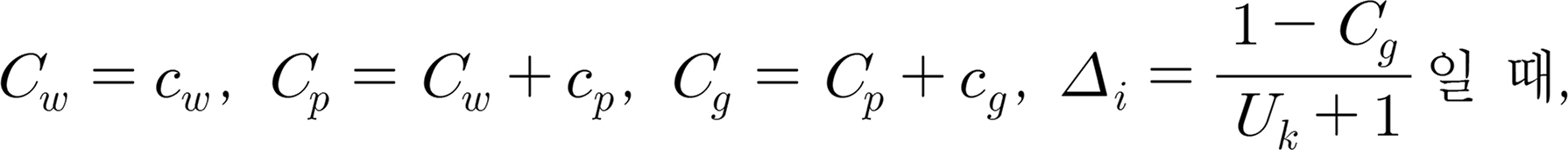
여기서, cw, cp, cg는 현재 해 유지, 입자 최적해 적용, 전체 최적해 적용 가중치를 나타내며,
Step 4 : 경로집합 품목의 중복할당 수량을 0으로 변경한다.
Step 4-1 :
Step 4-2 : i입자의 j군의 경로집합 품목의 중복할당 수량을 0으로 변경한다.
Step 5 : 모든 품목의
3.5 탐색정지 조건
해의 탐색 정지를 위하여 일반적으로 반복회수(세대 수) n을 지정하는 방법과 탐색 중 해의 개선 없이 동일한 최적해가 반복적으로 n회 나타났을 경우 정지하는 방법을 적용한다. 본 연구에서는 세대 수를 지정하여 탐색을 실시하고 해의 탐색을 정지시키게 한다.
4. 실험 및 분석
4.1 3 수준 시스템 실험
제안된 알고리즘의 실험을 위해서 Yun and Kim(2004)에서 적용한 시스템 구조를 활용하여 Chung(2015)에서 적용한 데이터를 사용한다. Figure 2는 계층이 3개인 시스템을 나타낸다. 시스템은 A, B, C 모듈로 구성이 되어 있으며, 모듈 A, B, C는 각각 3개, 2개, 2개의 하위 품목군으로 구성이 된다.
System structure in numerical example proposed at Yun and Kim(2004)
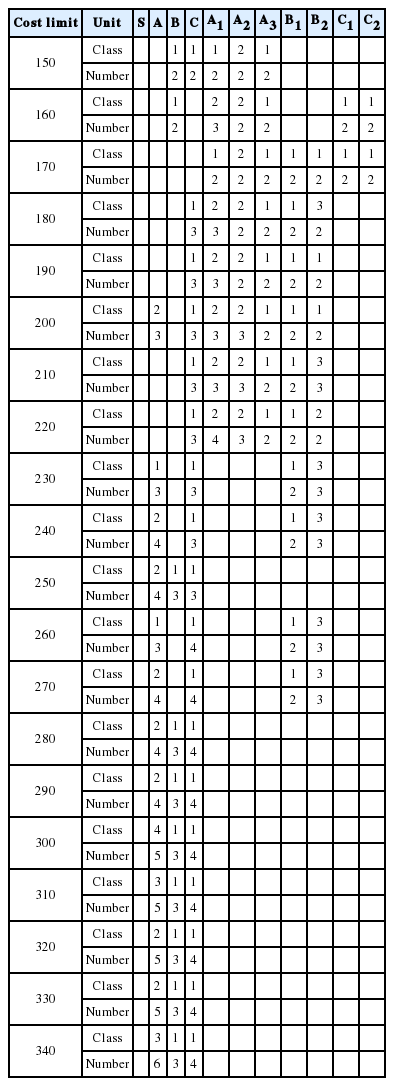
각 품목군은 Table 1과 같이 1~4종의 대안 부품의 적용이 가능한 것으로 하였다.
Input data of three-level system
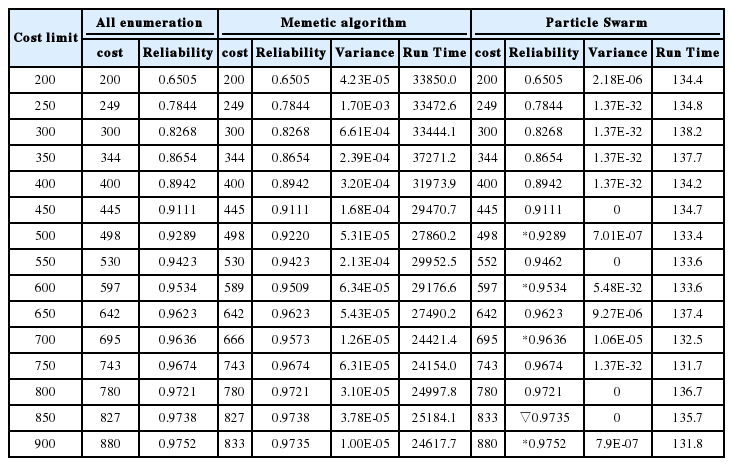
Table 1의 데이터를 바탕으로 비용한계를 150에서 340까지 10씩 증가시키면서 미미틱 알고리즘과 입자 군집 알고리즘과의 비교를 실시하였다. Table 2는 각 비용한계마다 초기난수를 달리하여 10회 반복실험을 실시한 결과 중 가장 좋은 해와 분산 그리고 해의 탐색시간 평균을 나타내고 있다. 비용한계 20가지 경우에서 미미틱 알고리즘과 입자 군집 알고리즘의 가장 좋은 해는 all enumeration 방법의 최적해와 모두 동일한 결과를 나타내었으며, 분산의 경우 입자 군집 알고리즘이 미미틱 알고리즘보다 적게 나타남을 알 수 있다. 세 번째 열에 탐색시간의 경우 입자 군집 알고리즘이 미미틱 알고리즘에 비해 절반 정도의 시간이 소요됨을 나타내고 있다.
Comparison result between MA and PS
Table 3은 Table 2의 각 비용한계별 중복할당 결과를 나타낸다. 비용 한계가 낮을 때 A 품목 군이 중복으로 선정되지 않았으나 비용이 증가함에 따라 A 품목 군이 선정되고 비용 변경에 따라 품목 군과 종이 변경되고 있음을 알 수 있다. A 품목 외 B, C 품목군도 비용한계가 증가함에 따라 모듈이 선택되어지는 경향이 나타났다. 이는 중복 수량이 증가할수록 하위 품목의 추가 비용이 급격히 증가하고 상대적으로 모듈의 경우 추가비용이 적게 소요되어 모듈이 중복 대상으로 선택되고 있음을 알 수 있다. 또한, 상대적으로 신뢰도가 낮은 A품목의 중복이 280 이후로 증가 또는 종류의 변경이 나타남을 알 수 있다.
Results of redundancy allocation
4.2 4수준 시스템 실험
Figure 3은 계층이 4개인 시스템으로 모듈과 부품이 15개로 구성이 되어 있다.
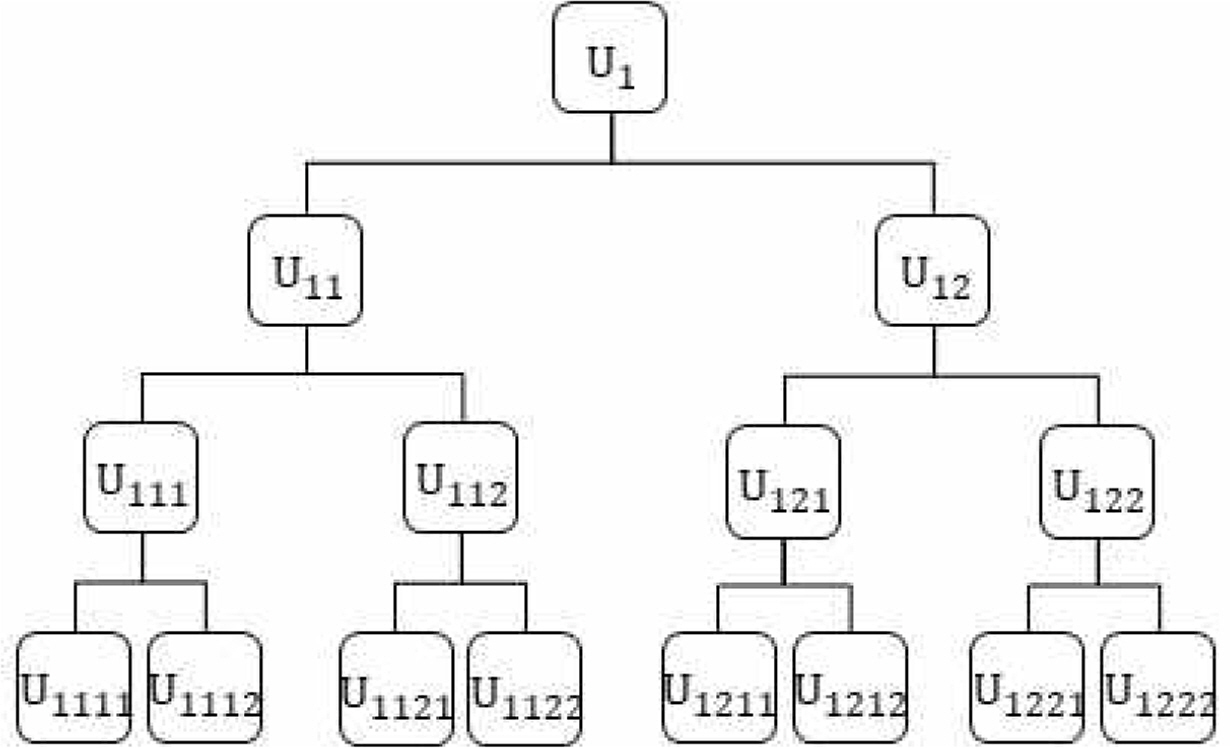
System structure in numerical example proposed at Kumar et al(2009)
Table 4는 Appendix에 Table 5의 데이터를 바탕으로 4 수준 시스템에 대한 실험 결과를 나타낸다. 15개의 비용 조건에서 입자 군집 최적화와 미미틱알고리즘을 비교한 결과 3가지 경우에서 입자 군집 최적화가 미미틱 보다 더욱 좋은 해(* 표시)를 나타내었으며, 1가지 경우에서 미미틱이 더욱 좋은 해를 나타내었다. 비용한계 550에서는 입자 군집 최적화의 경우 비용한계를 넘어서는 552의 결과가 산출되었다. 이에 대해 식(8)의 해의 평가시 벌금함수에 α값(1에서 1.2로 변경)을 크게 변경함으로써 enumeration의 최적 결과와 동일한 결과를 얻을 수 있었다. 실험의 결과에서 시스템이 복잡해짐에 따라 미미틱 알고리즘의 경우 탐색시간이 상당히 증가됨을 볼 수 있으며, 입자 군자 최적화의 경우 3수준과 비슷하게 나타났다. 이는 시스템의 복잡성으로 인해 유효해를 탐색하는데 필요한 시간이 증가하여 이러한 시간의 차이가 발생함을 나타낸다.
Comparison result between MA and PS
5. 결론 및 추후 연구과제
본 연구에서는 입자 군집 최적화 방법을 활용하여 다계층 시스템의 최적 중복 할당 방법을 다루었다. 특히, 동일한 기능을 수행하는 대안 부품이 존재할 경우 비용과 신뢰도 측면을 고려하여 최적화 방법을 제시하였다. 3수준과 4수준의 실험 예제를 통해 입자 군집 최적화 방법에 대한 결과를 검증하였으며, 기존에 제시된 미미틱 알고리즘과의 비교 결과 시스템의 구조가 복잡해 질수록 해의 질과 탐색 시간 측면에서 입자 군집 최적화 방법이 더욱 좋은 결과를 보여주었다. 본 연구에서는 한 개의 군에서 한 개의 종만을 선택해서 최적화하는 방법을 다루었다. 향후에는 한 개의 군에서 서로 다른 종을 섞어서 중복을 하는 경우와 가용도 측면에서의 변화와 수리 정책에 대해 고려해 볼 수 있을 것 같다.