역삼투압 해수담수화(SWRO) 플랜트에서 독립변수의 다중공선성을 고려한 예측모델에 관한 연구
A Study on the Prediction Model Considering the Multicollinearity of Independent Variables in the Seawater Reverse Osmosis
Article information
Trans Abstract
Purpose
The purpose of this study is conducting of predictive models that considered multicollinearity of independent variables in order to carry out more efficient and reliable predictions about differential pressure in seawater reverse osmosis.
Methods
The main variables of each RO system are extracted through factor analysis. Common variables are derived through comparison of RO system # 1 and RO system # 2. In order to carry out the prediction modeling about the differential pressure, which is the target variable, we constructed the prediction model reflecting the regression analysis, the artificial neural network, and the support vector machine in R package, and figured out the superiority of the model by comparing RMSE.
Results
The number of factors extracted from factor analysis of RO system #1 and RO system #2 is same. And the value of variability(% Var) increased as step proceeds according to the analysis procedure. As a result of deriving the average RMSE of the models, the overall prediction of the SVM was superior to the other models.
Conclusion
This study is meaningful in that it has been conducting a demonstration study of considering the multicollinearity of independent variables. Before establishing a predictive model for a target variable, it would be more accurate predictive model if the relevant variables are derived and reflected.
1. 서 론
기술의 발전에 따라 센서를 활용하여 수집되는 제조공정 데이터가 증가하고 있다. 이에 따라 여러 기업에서 공정 변수의 영향 분석 및 최적화를 통해 생산성 향상, 유지보수 정책 수립 등 실질적인 가치를 얻기 위한 노력이 증대되고 있다. 다단계 생산 공정(multi-stage process)에서 수집되는 공정데이터는 변수 간 강한 상관관계를 가지며 관계가 복잡하다(Pack and Byun, 2002). 이러한 공정데이터로 회귀모델을 구축할 시 다중공선성(multicollinearity)이 존재한다. 다중공선성은 다중회귀모델에서 추정계수의 분산을 증대시켜 결과적으로 독립변수의 신뢰도를 저하시키므로 회귀모델의 구축과정에서 세심한 대응과 검토가 필요하다(Ryu, 2008). 다중공선성이 존재하는 데이터로 모델링을 수행하는 것은 비효율적이며 통계적으로 유의미하지 않은 결과를 내놓을 가능성이 있다. 본 논문에서는 효과적인 분석과 신뢰성 있는 예측을 수행하기 위해 독립변수들의 다중공선성을 고려한 예측 모델에 관한 연구를 수행하였다.
다중공선성을 고려한 예측모델을 연구하기 위해 해수담수화플랜트에서 측정한 데이터를 활용하였다. 해수담수화플랜트의 공정데이터는 바닷물의 성분과 약품들의 화학작용을 통해 측정되는 성분들이 많다는 특징을 가지며 변수 간 강한 상관관계를 가진다. 해수담수화의 가장 대표적이며 주로 사용하는 기법으로는 증발법과 역삼투법이 있다(Kim, 2009). 해수담수화기술은 과거 열에너지를 이용한 증발법 위주로 기술이 개발되어 왔으나, 2000년대 전후로 멤브레인(membrane)을 이용한 역삼투법(reverse osmosis desalination technology, RO)이 시장을 주도하고 있다(Kim, 2017). 해수담수화플랜트를 구성하고 있는 다양한 구성기기 중 가동 정지의 주원인은 RO 멤브레인으로, 본 논문은 이를 포함하고 있는 RO 시스템을 연구대상으로 선정하였다. RO 멤브레인을 포함하는 RO 시스템에는 해수담수화플랜트 가동 시 내부 차압의 변화가 발생한다. 적절한 유지보수가 이루어지지 않는 경우 내부 차압이 허용 가능 차압 기준보다 높아지게 되며 해당 수준을 넘어설 경우 플랜트 가동이 중단된다. 플랜트 가동이 중단되는 경우 막대한 손실이 발생하므로 차압이 일정 기준을 넘기 전에 적절한 유지보수를 수행해야 한다.
따라서 본 논문에서는 차압을 목표변수로 한 독립변수들의 다중공선성을 고려한 예측 모델링을 수행하였다. 해수담수화의 RO 시스템으로부터 측정된 독립변수들의 다중공선성을 제거하기 위해 요인분석으로 각 RO 시스템의 주요 변수를 추출한 후 공통변수를 추출하였다. 그리고 추출된 변수들을 이용하여 회귀분석, 인공신경망(artificial neural network, ANN), 서포트벡터머신(support vector machine, SVM)으로 예측모델을 구축하였다. 최종적으로 구축된 모델들의 평균제곱근오차(root mean square error, RMSE)를 도출한 후 이를 비교하여 모델의 우수성을 파악하였다.
2장에서는 해수담수화시스템에 관련된 연구동향과 독립변수 간 다중공선성이 존재할 시 변수선택에 관련된 문헌들을 소개한다. 3장에서는 본 논문에서 다루는 연구 대상 및 데이터를 소개하고 연구 진행방법을 다룬다. 4장에서는 요인분석을 통해 주요변수를 추출하고 세 가지 예측모델을 구축하여 수행하고 RMSE 값을 도출한다. 마지막으로 5장에서는 결론을 통한 기대효과를 파악하고 추후 연구과제에 대하여 제시한다.
2. 관련문헌 연구
크게 두 가지에 관한 문헌 자료들을 검토하고 분석하였다. 첫 번째로 연구 대상인 해수담수화플랜트에 관련된 연구를 진행하였다. 현재 해수담수화 기술은 기존 전력망을 이용하는 기술에 국한되어 있으며 신재생에너지를 이용한 에너지 공급 시스템의 개발이 필요한 실정이다(Oh et al., 2019). Hwang and Kim(2016)은 국내외의 역삼투 공정 현황과 해수담수 공정에 소모되는 에너지 소모 저감에 대해서 논의하였다. Kang et al.(2011)은 해수담수화 역삼투막 공정의 CaCO3 무기질 오염에 대한 스케일 억제제 효과를 분석하였다. Choi et al.(2019)은 국내에 설치된 중형급 해수담수화플랜트를 대상으로 연간 에너지 사용량 등의 운전결과를 도출하고, 이를 기반으로 시설 용량별 건설비 및 유지관리비를 산정하였다. 그 결과 생산수 단가는 생산용량이 증가할수록 감소하는 경향을 보였다. 이와 같이 해수담수화플랜트의 경우 기술 개발 및 경제성 분석에 관련된 분야로 다양한 연구가 수행되었다.
두 번째로 다중공선성을 고려한 방법론에 관한 문헌연구를 수행하였다. 다양한 독립변수들의 차원을 축소하며 다중공선성을 고려한 방법론으로는 주성분분석(principal component analysis), 요인분석(factor analysis), 변수선택(variable selection) 등이 있다. Kim and Lee(2012)는 주성분분석을 통하여 출입인원에 대한 보안성 확보방안을 제시하기 위한 연구를 진행하였다. Shin et al.(2012)은 입목축적과 산림관리정책 간의 전이 함수를 도출하기 위한 선행연구로써 입목축적 변화를 유도하는 산림산업 간 다중공선성의 문제를 해결하기 위해 주성분분석을 실시하였다.
Lam et al.(2010)은 건설업계에서 제한된 예산으로 고객을 만족시키기 위해 의사 결정자의 주관적 판단을 정량화 한 후 주성분분석을 통해 다중공선성을 제거하였다. 그 후 재료 공급자를 선택하는 모델을 구축하는 연구를 수행하였다. Chattopadhyay and Chattopadhyay(2012)는 인도 동부 지역의 월별 오존 농도를 예측하기 위해 주성분분석으로 독립변수인 구름, 온도, 강수량 등의 다중공선성을 제거하고 다층 퍼셉트론 형태의 인공신경망을 개발하였다. Sopipan(2013)은 태국의 증권거래소에 대한 정확한 수익을 예측하기 위해 주성분분석을 적용하여 다중공선성으로 발생할 수 있는 여러 가지 문제점을 제거한 높은 성능의 회귀식을 도출하였다. Lee(2009)는 노인장기요양보험제도에서 서비스에 대한 수급권리가 있는 1~3등급의 노인이 서비스 이용을 결정하게 되는 요인을 다층모델을 통해 분석하였다.
주성분분석 외에도 다중공선성을 제거하기 위해 다양한 방법론에 대한 연구가 수행되었다. Kim et al.(2018)은 회귀모델로 호우피해함수를 제안하면서 다중공선성이 존재할 때 모델 개발의 어려움을 논하였다. 이를 개선하기 위한 방법으로는 자료 통합 및 주성분회귀모델과 능형회귀모델로 최종 호우피해함수를 개발하는 과정을 소개하였다. Lee et al.(2015)은 불량 발생 원인이 되는 중요 공정변수와 규칙을 찾기 위해 다중공선성과 불균형분포의 특징을 가지는 공정데이터의 효과적인 분류 모델 구축을 위한 데이터마이닝 절차와 방법을 제안하였다.
이처럼 다양한 분야에서 독립변수들의 다중공선성 제거 방안 연구와 변수 축소 및 잠재적 요인을 도출하기 위한 연구가 수행되고 있다. 그에 비해 다단계 생산 공정에서 수집된 공정 데이터에 대한 연구 및 공정 데이터의 다중공선성을 고려한 연구는 찾아보기 어렵다. 또한 다른 플랜트 공정의 유지보수에 대한 연구는 다양하게 진행되었으나 해수담수화플랜트의 유지보수에 대한 연구는 미비하다. 따라서 본 논문에서는 요인분석을 적용하여 다단계 생산 공정에서 수집된 독립변수 간 다중공선성을 고려한 예측모델을 구축하고자 하였다.
3. 연구 방법 및 절차
3.1 연구대상 소개
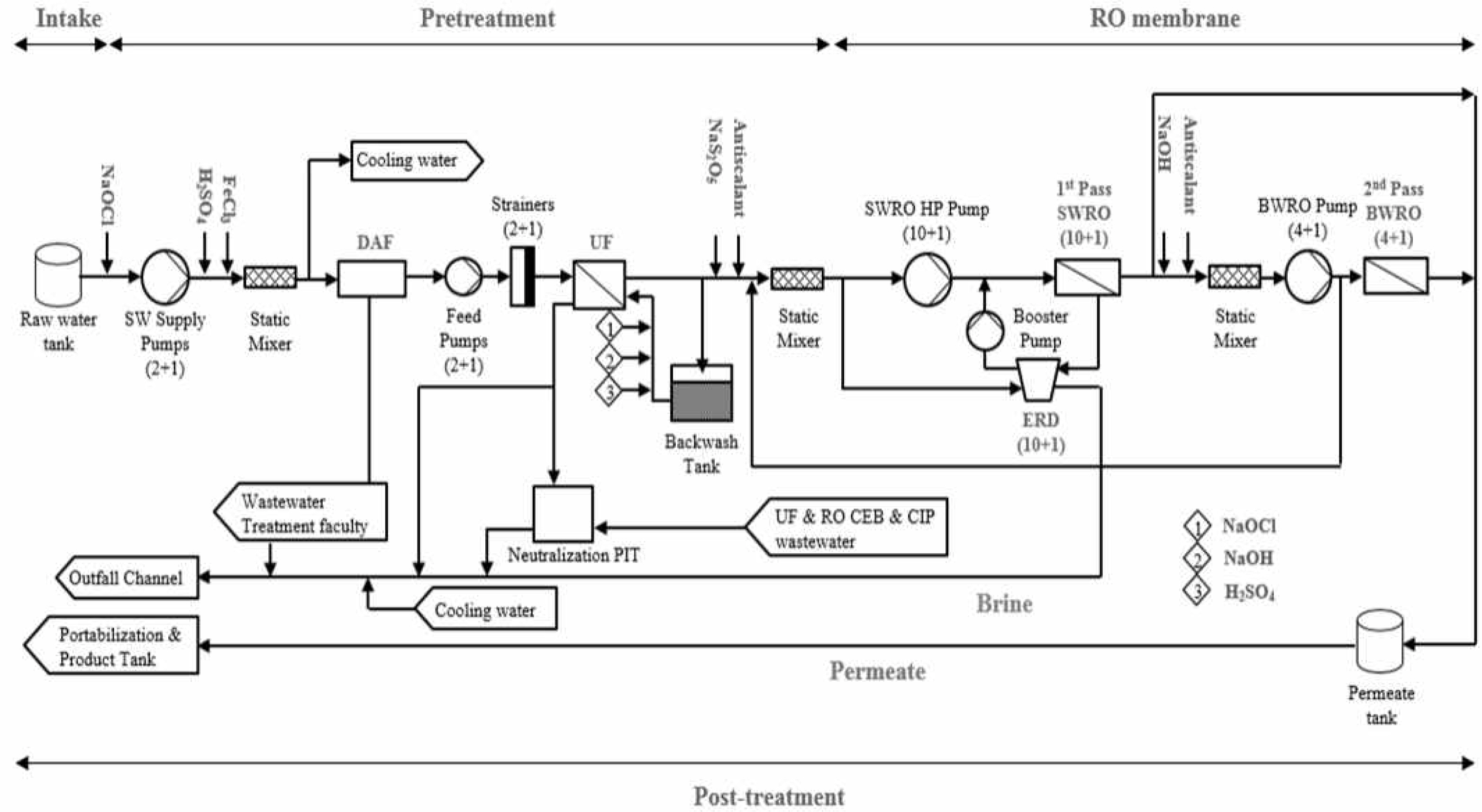
해수담수화플랜트 기술은 물 부족을 해소하기 위한 방안 중 가장 주목받고 있는 기술이다(Lee, 2018). 2000년 이후 에너지 요구량이 적고 환경적 제한이 적은 역삼투 기술을 중심으로 한 막분리 해수담수화 기술에 대한 수요가 크게 증가하고 있다(Sohn, 2016). 역삼투 방식은 삼투현상과 반대로 강제로 가하는 압력에 의해 물속 불순물 농도를 높은 쪽에서 낮은 쪽으로 이동시키는 정수방법이다. 역삼투압 해수담수화플랜트 설비는 크게 용존염 제거를 위한 역삼투막 모듈, 전처리 설비, 그리고 해수를 공급하기 위한 펌프로 구성되어있다. 막의 성능을 안정적으로 유지하기 위한 전처리 설비는 대표적으로 한외여과(ultra-filtration, UF)와 가압부상조(dissolved air flotation, DAF)가 있다. 역삼투막 모듈로 해수를 공급하기 위한 펌프는 수중펌프(submersible pump), 고정속도형펌프(fixed speed pump) 등이 존재한다. 해수담수화플랜트 공정에 대한 자세한 사항은 Figure 1을 통해 볼 수 있다.
Process Diagram of Seawater Desalination Plant
역삼투 공정의 필수 요소인 역삼투막은 막 오염(fouling)에 취약하며 해수담수화 플랜트 가동 정지의 주원인이다. 수처리에 사용되는 멤브레인은 액체 또는 기체의 특정 성분을 선별적으로 통과시켜 혼합물을 분리할 수 있는 액체막 또는 고체막으로 필터 역할을 한다. 해수담수화플랜트 가동 정지의 주원인은 RO 멤브레인으로 이를 포함하고 있는 RO 시스템을 연구대상으로 선정하였다. 선정된 RO 시스템은 최소 1개 이상의 RO 멤브레인을 가지며 실제 분석 대상에는 7개의 RO 멤브레인이 직렬로 연결되어 있다.
3.2 데이터 수집 및 적용범위
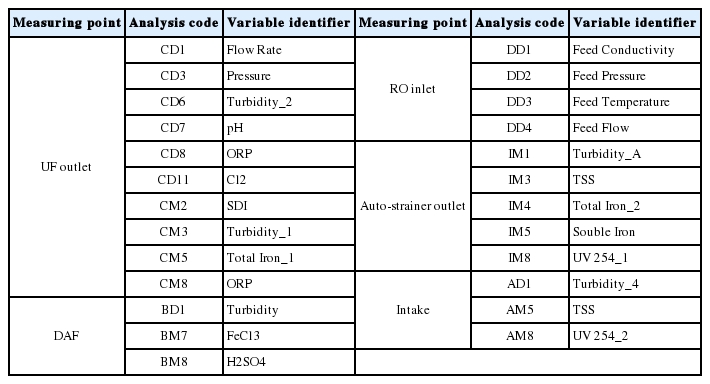
연구대상인 RO 시스템은 DCS(distributed control system)와 Manual 방식으로 데이터가 수집된다. DCS로 수집되는 데이터는 센서를 통해 실시간으로 측정되는 값이며 Manual 방식은 실제 물을 채취하여 성분을 분석한 것이다. 데이터 수집 기간은 2011년 9월부터 2016년 2월까지이며 약 30개 이상의 변수로 구성되어 있다. 변수에 대한 자세한 설명은 기업보안상 서술하지 않는다. 분석결과의 신뢰성을 높이기 위해 분석에 반영되는 변수의 데이터 수를 최소 500개 이상으로 설정하여 그 이하의 데이터를 가지고 있는 변수는 사전에 삭제하였다. 최종 선정된 변수는 25개이며 Table 1과 같다. RO inlet, UF outlet 등 6개의 영역은 데이터가 측정되는 지점을 나타내며 각 지점마다 측정되는 변수는 각각 분석 코드를 부여하였다. 분석 코드의 첫 번째 알파벳은 측정지점을 의미하며, 두 번째 알파벳은 측정방법을 의미한다. 측정방법에 따라 DCS 방식은 “D”로 Manual 방식은 “M”으로 표기하였다.
Independent Variables and Analysis Codes in Measuring Points
3.2 연구 진행 과정
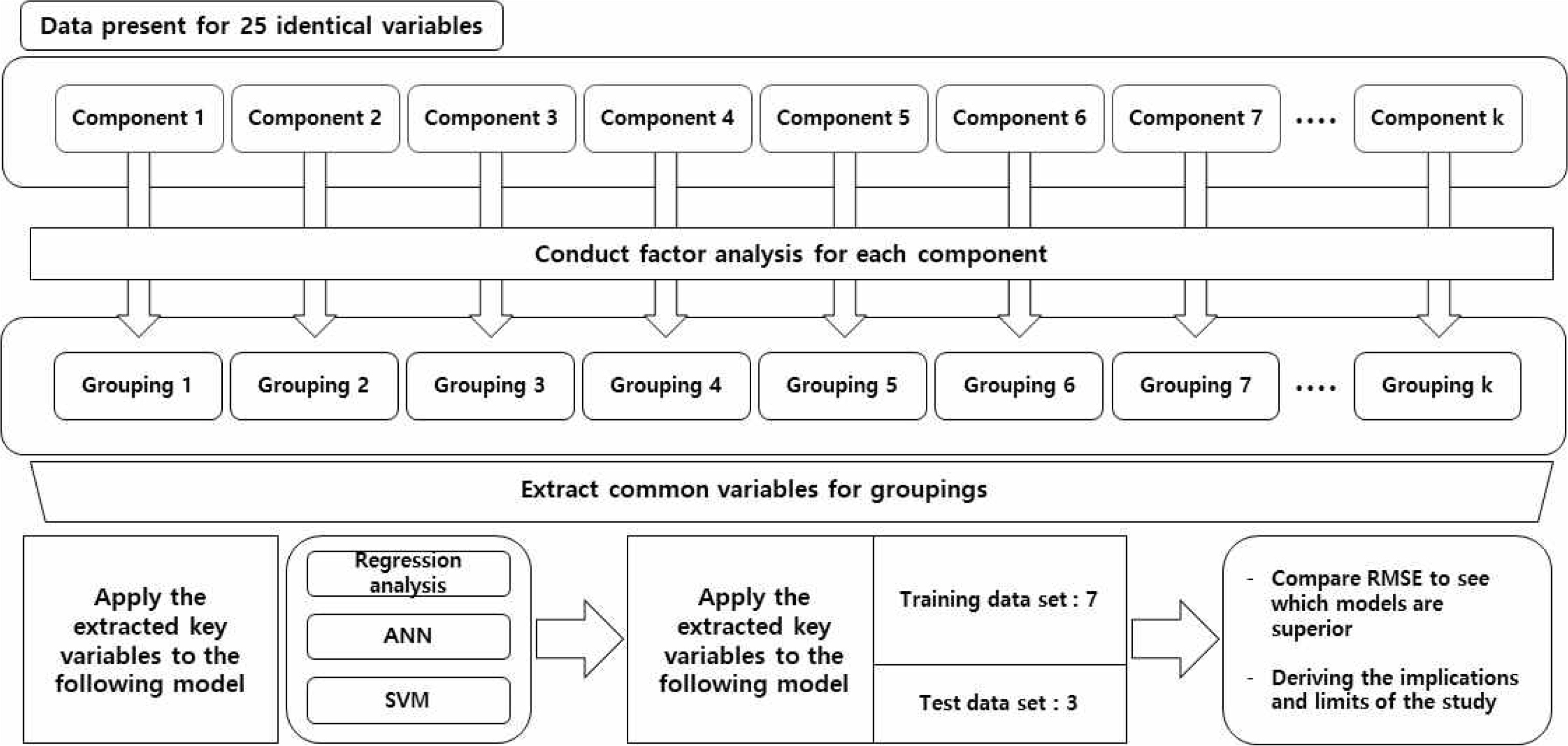
연구진행 과정은 Figure 2와 같다. 각 Component는 개별 RO 시스템을 의미하며 RO 시스템은 최소 1개 이상의 멤브레인으로 구성되어 있다. 실제 분석 대상은 11개의 RO 시스템으로 구성되어 있으나, 보안상의 이유로 RO 시스템 #1, RO 시스템 #2에 대한 변환된 데이터를 분석에 반영하였다.
Research Process
RO 시스템 #1과 RO 시스템 #2를 각각 요인분석을 실시하여 주요변수를 추출하고 이를 비교하여 공통인자를 도출한다. 공통으로 도출된 인자를 독립변수로 하여 목표변수인 차압에 대한 예측 모델링을 수행한다. 예측 모델링에 반영될 통계적 방법론은 회귀분석, ANN, SVM이며 최종적으로 RMSE 값을 도출하여 어느 모델이 우수한지 파악하고 해당 연구의 시사점 및 한계점을 도출한다.
사용된 방법론인 요인분석은 변수들 간의 상관관계를 바탕으로 정보의 손실을 최소화하며 적은 수의 요인으로 자료의 변동을 설명하는 기법이다. 데이터 변동성을 설명할 수 있는 잠재적인 인자를 식별하며 자료 요약, 변수 구조파악, 변수 제거, 측정도구의 타당성 검증을 목적으로 사용된다. 본 논문에서는 측정변수들 간 유사한 요인들을 묶어 차원축소를 진행하기 위해 이를 수행하였으며 각 RO 시스템의 비교분석을 통해 공통인자를 추출하였다.
4. 실험분석 및 결과
4.1 주요인자 도출
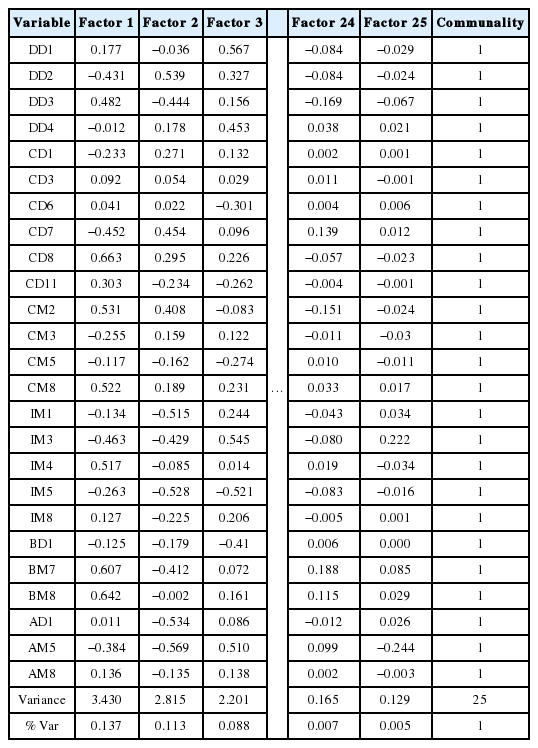
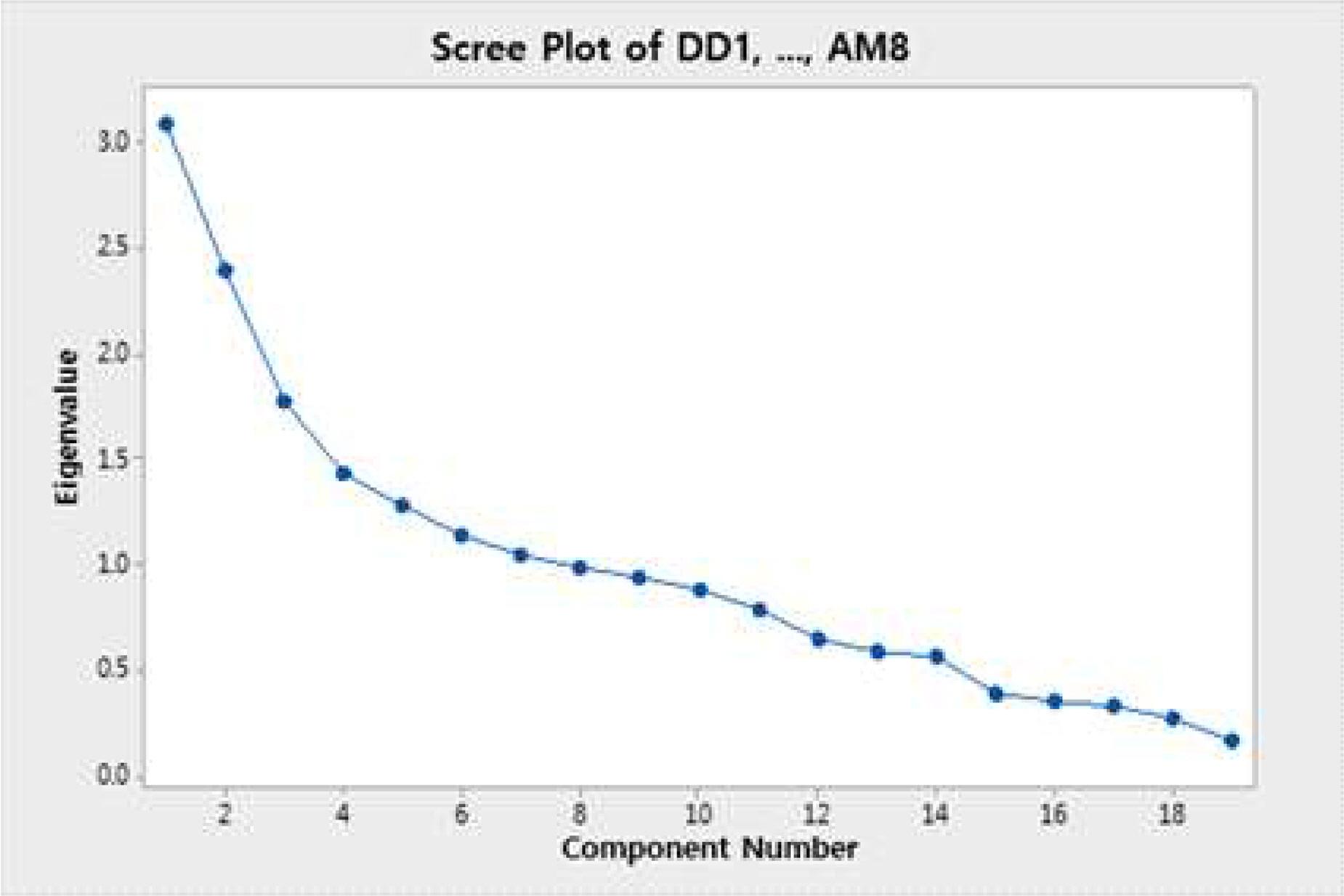
RO 시스템 #1과 RO 시스템 #2에 대해 각각 요인분석을 진행하였다. 분석 프로세스와 해석하는 방법이 동일하므로 RO 시스템 #1에 대해 분석한 내용을 상세히 기술하고 RO 시스템 #2는 결과만 추출하여 비교하고자 한다. RO 시스템 #1의 비회전인자 적재 및 공통성은 Table 2와 같다. 해당 분석은 각 변수의 전체 데이터 개수인 1,072개에서 752개의 사례를 사용하고 나머지 320개 사례는 결측값으로 인해 제외하였다. Factor 24와 Factor 25가 설명하는 변동성 비율은 매우 작기 때문에 두 인자는 제거해도 무방하며 다수의 요인들이 제거될 필요가 있다. 고유값 및 스크리 도표 확인을 통해서 인자추출 개수를 결정한다. Figure 3은 RO 시스템 #1에 대한 스크리 도표 결과를 나타낸다. 스크리 도표를 통해 요인번호 9까지 고유값이 1보다 크다는 것을 확인할 수 있다.
Unrotated Factor Loadings and Communalities of RO System #1
Scree Plot of RO System #1
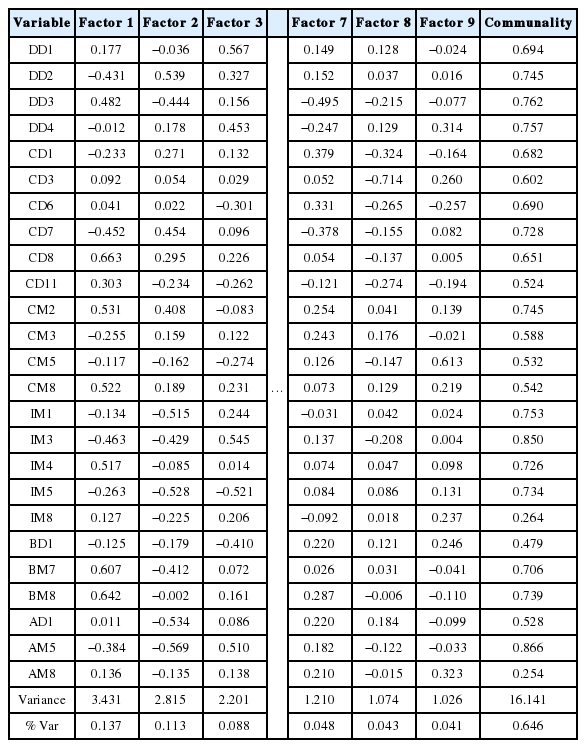
스크리 도표와 고유값 확인을 통해 추출 인자의 수를 9개로 결정하고 varimax 회전을 적용하여 분석하였으며 그 결과는 Table 3과 같다.
Varimax Rotated Factor Loadings and Communalities of RO System #1
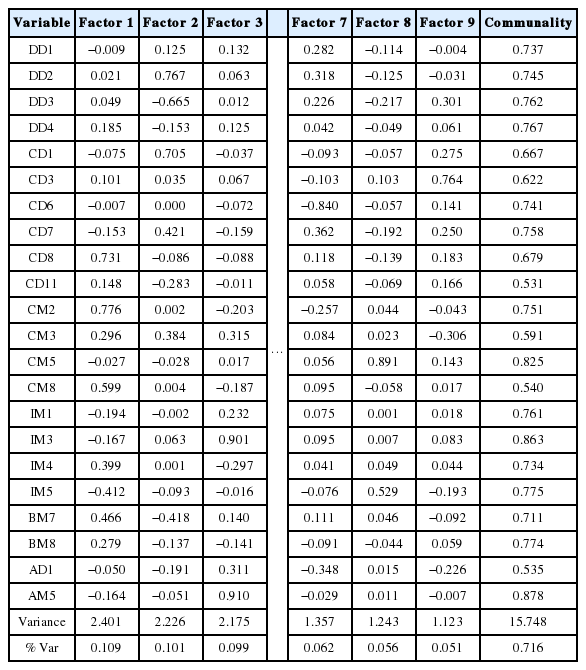
공통성이 0.5 이하의 변수인 IM8, BD1, AM8을 제거한 후 다시 분석을 진행하였으며 그 결과는 Table 4와 같다. 분석에 반영된 각 변수는 865개의 데이터가 사용되었고 나머지 207개에 대해서 결측치가 존재하였다. 분석 결과 회전인자는 모든 변동성의 71.6%를 설명하고 있으며 공통성은 모두 0.5 이상이므로 모든 변수를 적절히 표현하고 있다.
Varimax Rotated Factor Loadings and Communalities of RO System #1 (Variable removal)
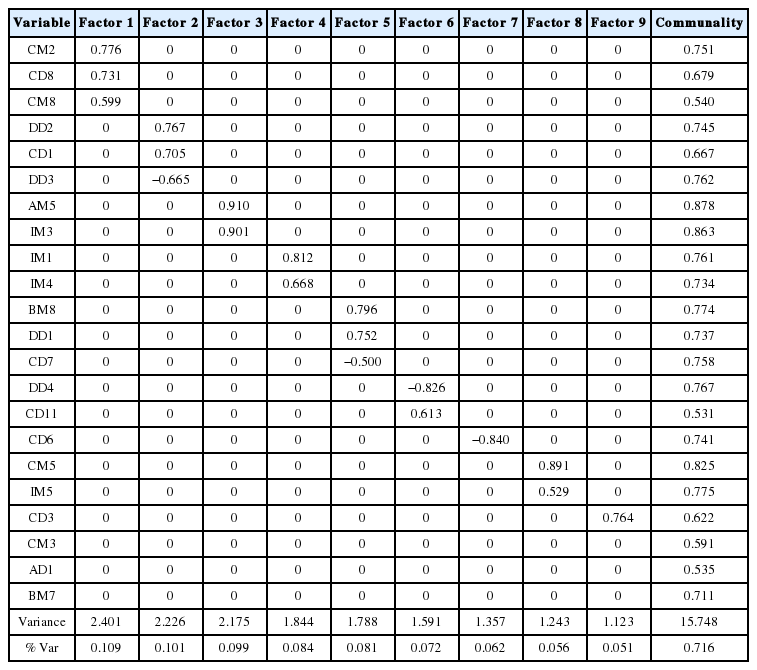
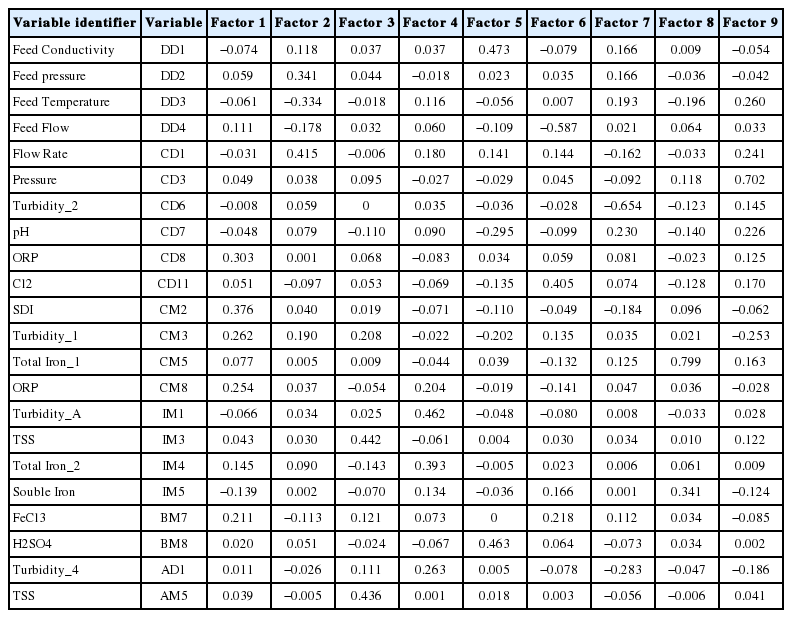
정렬된 인자의 경우 모든 인자의 최대 절대 적재를 기준으로 수행되며 RO 시스템 #1의 정렬된 varimax 회전인자 적재 및 공통성의 결과를 Table 5에 나타내었다. Factor 1에서 절대 적재값이 가장 높은 변수가 정렬순서상 가장 첫 번째로 출력이 된다. Factor 1의 CM2, CD8, CM8 변수에서 큰 양의 적재값을 가진다. Factor 2에서는 DD3 변수에서 음의 적재값을 가지고 DD2, CD1에서 양의 적재값을 갖는 것으로 확인된다. RO 시스템 #1의 요인분석 결과 총 9개의 요인이 추출되었으며 각 요인에 묶이는 변수들을 파악할 수 있다. Table 6은 인자 점수 계수의 표로 인자 계산 방식을 나타낸다.
Aligned Varimax Rotated Factor Loadings and Communalities of RO System #1
Factor Score Coefficients of RO System #1
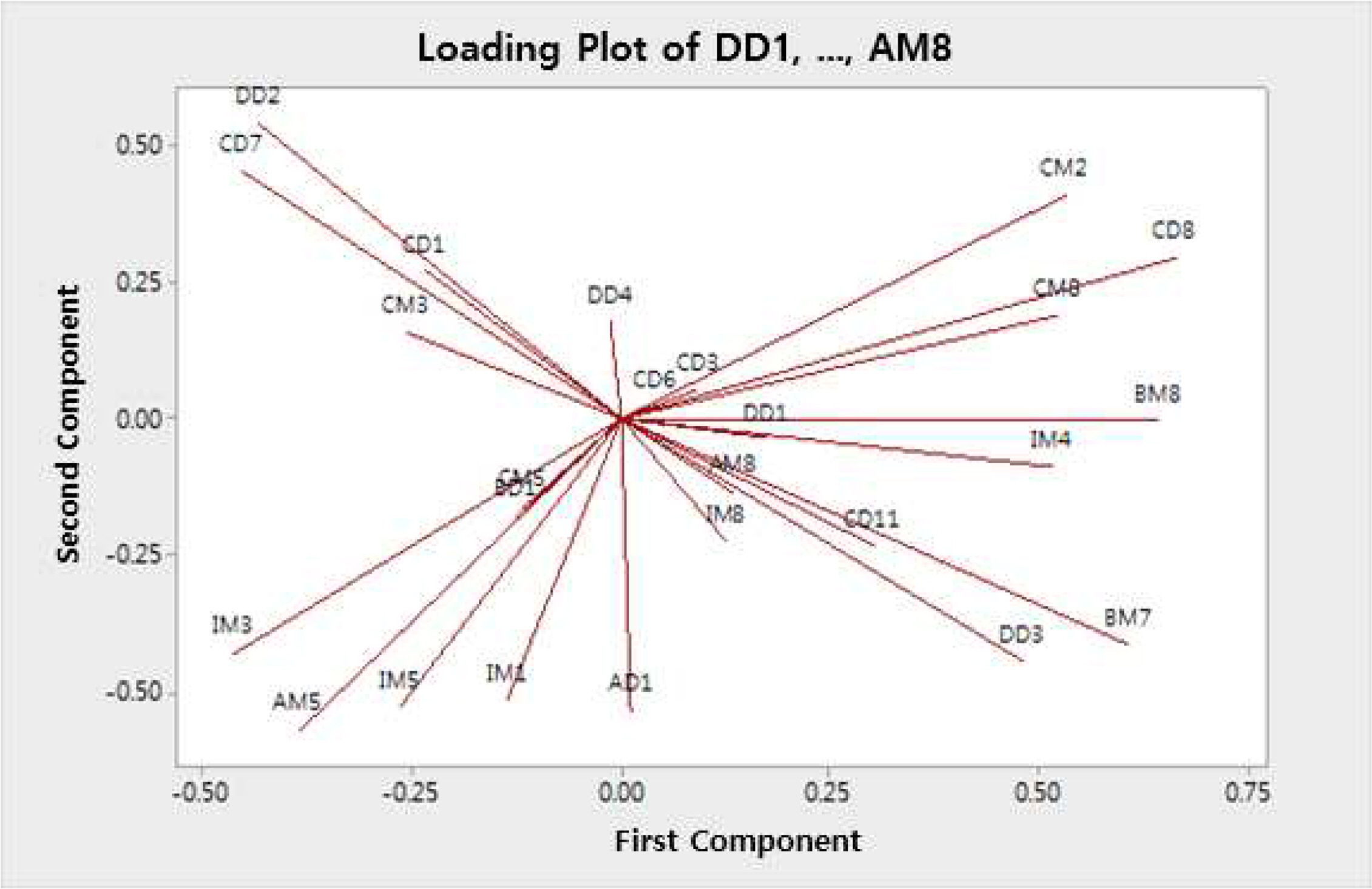
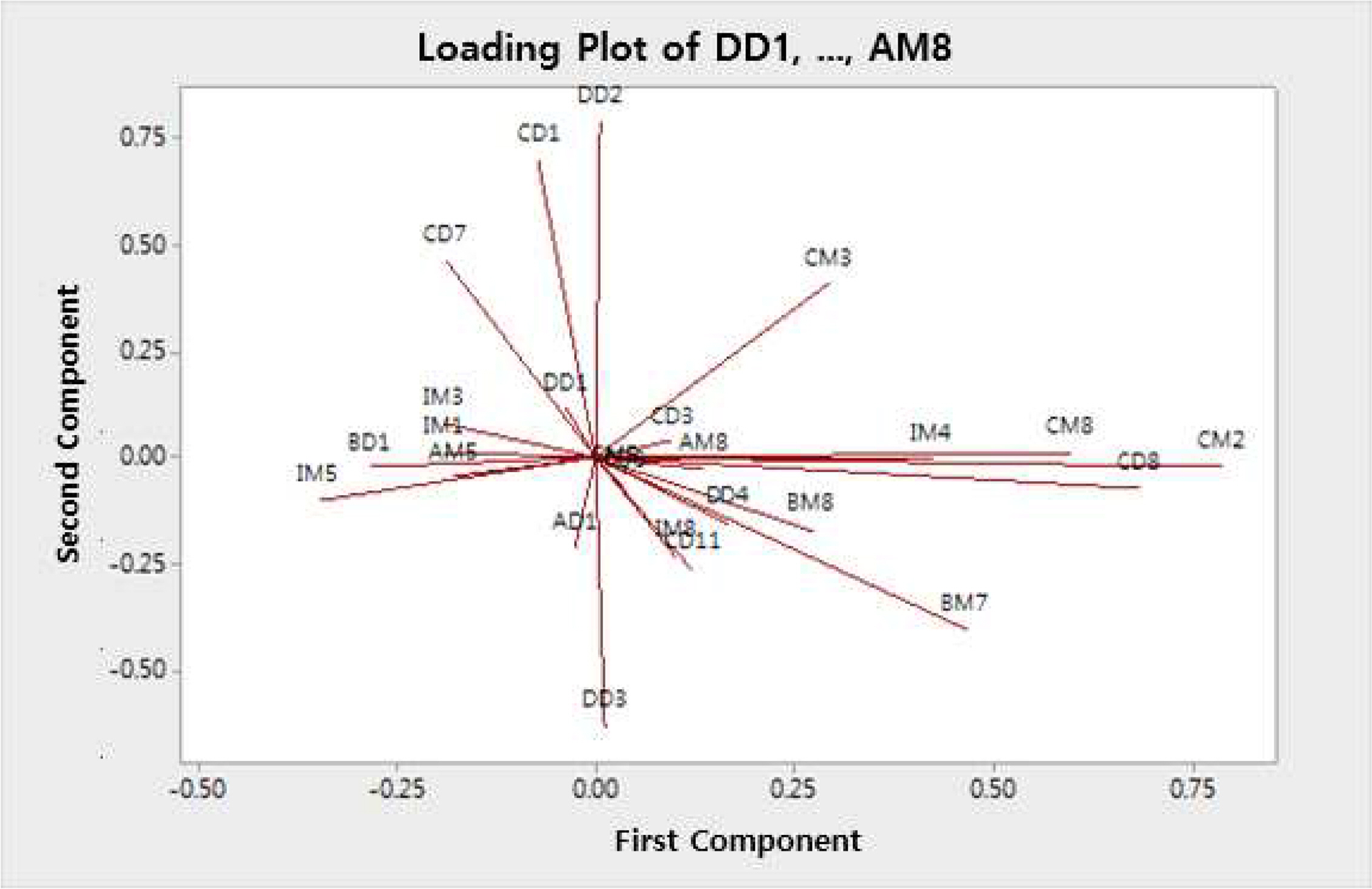
아래의 그림들은 각 Step별 적재 그림을 나타낸다. Figure 4의 경우 비회전 요인 적재 그림으로 모든 변수들이 전 방위로 퍼져있어 변수들의 상관관계를 파악하기에 어려움이 있다. Figure 5는 스크리 도표 및 고유값 확인을 통해 추출인자 개수를 9개로 설정한 후 varimax 회전을 수행한 적재그림이다. Figure 4에 비해 변수들끼리 모여 있는 군집형태를 볼 수 있다. Figure 6은 varimax 회전 후 공통성이 0.5 이하인 IM8, BD1, AM8 변수를 제거하고 다시 요인분석을 실시한 결과이다.
Unrotated Factor Loadings Plot of RO System #1
Varimax Rotated Factor Loadings Plot of RO System #1
Varimax Rotated Factor Loadings Plot of RO System #1 (Variable removal)
4.2 결과 비교를 통한 공통 주요인자 도출
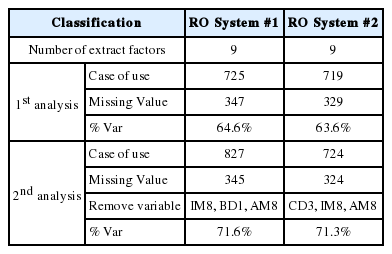
RO 시스템에 따른 요인분석 결과는 Table 7과 같다. 추출 인자 개수는 동일하게 9개이며, 분석 절차에 따라 진행될수록 변동성(% Var)의 값이 증가하는 것을 볼 수 있다.
Results of Factor Analysis of Two RO Systems
Table 8은 RO 시스템에 따른 정렬된 회전 인자의 결과 및 각 RO 시스템의 추출된 공통인자를 보여준다. 기재된 변수들은 서로 연관성이 높은 변수들로 분류되었으며 RO 시스템에 따라 다소 상이한 분류 형태를 보인다. 따라서 RO 시스템 #1과 RO 시스템 #2를 모두 설명하는 예측 모델링을 수행하기 위해 공통되는 추출인자를 차압에 대한 예측모델링의 독립변수로 사용한다.
Aligned Varimax Rotated Factor and Common Extraction Factor of RO System #1 & #2
4.3 주요인자의 통계적 모델 적용
본 절에서는 요인분석을 통해 RO 시스템 #1과 RO 시스템 #2에서 공통적으로 포함된 6개 공통추출인자의 12개 변수를 독립변수로 하여 목표변수인 차압에 대한 예측모델링을 수행하였다. 다중공선성 제거를 위해 요인분석을 실시하여 인자의 개수를 축소한 후 추출된 12개의 공통추출인자를 독립변수로 사용하였다. 각 시스템 별, 약 만여 개의 데이터가 사용되었으며 분석을 위해 R 3.3.0을 사용하였다. 최종적으로 구축된 모델은 30번 반복을 통해 평균 RMSE 값을 도출하였으며 Table 9에 공통 추출인자에 대한 RMSE 값을 비교하였다. 비교 결과, 전반적으로 SVM이 RMSE 지표 관점에서 다른 모델에 비해 우수한 것으로 나타났다.
Average RMSEs of common extraction factor
5. 결론 및 추후 연구과제
다중공선성이 존재하는 데이터의 경우 모델링을 수행하는 것이 통계적으로 유의미하지 않은 결과를 내놓을 가능성이 있다. 다양한 분야에서 독립변수의 다중공선성 제거를 위한 연구가 많이 수행되고 있으나 다단계 생산 공정에 적용된 연구는 미비하다. 또한 다양한 플랜트설비의 유지보수에 대한 연구 중 해수담수화플랜트에 관한 연구는 찾기 어려운 실정이다. 따라서 실제 환경에서 수집된 해수담수화플랜트 공정 데이터를 활용하여 변수 간 존재하는 다중공선성을 제거하고 유지보수를 위한 효과적인 예측모델을 구축하였다.
본 논문에서는 해수담수화플랜트에서 독립변수의 다중공선성을 고려한 예측모델에 대한 연구를 진행하였다. 독립변수들의 다중공선성을 제거하기 위해 요인분석을 적용하였으며 각 RO 시스템의 주요변수를 추출한 후 각 RO 시스템의 비교분석을 통해 공통 변수를 추출하였다. 그 후 목표변수인 차압의 예측모델링에 공통으로 추출된 독립변수를 반영하였다. 예측모델링을 수행하기 위해 회귀분석, ANN, SVM으로 모델을 구축하였으며, 구축된 모델의 RMSE 값을 구하였다. RMSE 지표 관점에서 값을 비교한 결과, 전반적으로 SVM이 다른 모델에 비해 우수하였다.
본 논문은 독립변수를 고려한 목표변수 예측모델에 대한 실증연구를 수행했다는 것에 의미가 있다. 일반적으로 연관되는 독립변수를 파악하기에 어려움이 존재하나, 공정 데이터의 경우 모니터링을 통해 독립변수를 파악할 수 있다. 해수담수화플랜트의 가동이 중단된 후 정상상태로 되돌리기 위해서는 막대한 시간과 비용이 소요되므로 적절한 시기에 유지보수를 진행하는 것이 중요하다. 파악되는 다양한 독립변수가 존재하는 조건에서 관련된 변수들만 추출하여 반영한다면 비교적 정확한 예측모델 구축이 가능하므로 해당 조건을 고려하는 예측모델을 구축하면 플랜트 설비의 효과적인 유지보수 정책 수립에 도움이 될 것이라고 기대된다.
반면 데이터 분석을 통해 형성된 그룹에 대한 물리적, 기술적 이유를 알 수 없다는 한계가 존재한다. 또한 추출된 요인은 실제 측정되는 값이 아니기 때문에 해당 값을 파악할 수 있는 추가적인 연구가 필요하다. 요인분석을 통해 추출된 요인과 관련된 잠재적 원인을 파악한다면 그 원인을 중심으로 실제 변수들을 조합하여 새로운 예측모델을 개발할 수 있을 것으로 기대된다.