2.1 수능 점수 체제의 변천

한국의 수능은 국무총리 산하 경제․인문사회연구회 소속의 정부 출연 연구기관인 평가원에서 주관하는 대학입시 표준화 시험이다. 수능 이전에 전국적으로 통일된 시험이었던 대학입학예비고사(1969~1981학년도)와 대학입학학력고사(1982~1993학년도)는 추론 없이 암기만을 강요한다는 문제가 있었다. 이를 해결하기 위하여 1980년대 후반부터 연구가 시작되어 1990년부터 1992년까지 7차례의 수능 ‘실험평가’가 실시되었다. 수능의 개념을 '사고력을 측정하는 발전된 학력고사'로 정립하였으며 대학교육의 수학에 기초가 될 보편적 학력을 측정하고, 학교에서 배운 능력을 평가하며, 고교 교육과정의 내용과 수준에 맞춰 출제하는 것을 목표로 하였다.

1994학년도부터 2022학년도까지 실시한 수능 점수 체제의 분류는 KICE(2004, 2019), Yang(2010) 등의 연구를 참고하여 본 논문에서는 다음의 3단계로 구분하였다.

1단계는 1994~1998학년도 수능에 해당하며 원점수 중심의 시기였다. 1994학년도에 최초로 수능을 실시하였으며 2회를 응시하여 자기에게 유리한 한 개의 성적만 선택하여 대학에 제출하는 방식이었다. 계열 구분 없이 공통으로 출제하여 모든 수험생이 같은 시험문제를 풀었다. 1995학년도부터 인문, 자연, 예·체능 3가지 계열로 구분하여 실시하였고 계열별로 총점 및 백분위, 영역별 원점수 및 백분위를 제공하였다.

2단계는 1999~2004학년도 수능에 해당하며 원점수에서 표준점수로 전환하는 시기였다. 계열 구분은 지속되었으며 6차 교육과정에 따라 선택과목 제도가 도입되었던 시기였다. 인문계와 자연계에 선택과목 제도를 도입하면서 선택과목의 유불리를 보완하기 위하여 표준점수 제도를 처음으로 도입하였고 표준점수의 평균은 모든 영역에서 50점이었고 표준편차는 10점이었다. 만점자의 표준점수 총점이 400점이 되도록 영역별 가중치를 부여한 변환표준점수 제도를 도입하였다. 2002학년도부터 원점수를 제외한 표준점수, 백분위, 변환표준점수는 모두 정수로 통지하였으며 ‘9등급제’를 처음으로 실시하였다. 영역별 등급은 소수 둘째 자리(소수 셋째 자리에서 반올림)까지 산출된 변환표준점수에 의한 등급이고 종합등급은 5개 영역별 변환표준점수를 합한 점수에 의한 등급이었다. 2004학년도에는 문항별 배점을 정수화하여 원점수 자체도 정수가 되고 정수로 된 변환표준점수 기준으로 등급을 구분하였다.

3단계는 2005학년도부터 현재까지의 수능으로 원점수는 공개하지 않는 표준점수 중심의 시기이다. 7차 교육과정이 적용되어 인문계, 자연계, 예·체능계로 구분된 계열 구분이 없어졌다. 원점수, 변환표준점수, 표준점수에 의한 백분위 및 종합등급은 통지하지 않고 영역/과목별 표준점수, 백분위, 등급만을 통지하였고 2022학년도까지 이러한 방식은 지속되어 왔다(단, 2008학년도에는 등급만 통지). 2014학년도 수능에서 언어, 수리, 외국어 영역의 명칭을 국어, 수학, 영어 영역으로 변경하고 수준별 수능을 실시하였다. 2017학년도 수능부터 한국사 영역을 필수로 지정하고 절대평가로 변경하였으며 2018학년도부터 영어 영역, 2022학년도부터 제2외국어/한문 영역을 추가하여 절대평가로 변경하였다. 절대평가로 평가하는 영역의 등급 구분점수는 미리 공개하고 있으며 절대평가 역시 9등급으로 구분하여 통지한다.

2.2 수능 점수 체제 관련 선행 연구

수능 점수 체제에 관한 기존의 연구는 수능 2단계 표준점수 도입 시기에 활발히 진행되었고 수능 3단계에서는 선택과목별 수험생의 학업능력 차이를 표준점수에 어떻게 반영할 것인지에 관한 연구가 많이 진행되었다.

Kim et al.(1998)은 몇 번의 전문가 협의를 통하여 1999학년도 수능 성적을 의미 있게 해석하고 보고할 수 있는 시험점수 체제 개선안을 발표하였다. 개선안에서는 평균이 50이고 표준편차가 10인 T 점수 척도를 표준점수로 채택하고 선택과목이 있는 경우 공통과목 점수를 활용하여 선택과목 점수를 통계적으로 조정하는 방법으로 검사점수 조정 공식을 산출하였다. 지원자에게는 계열별로 원점수, 원점수에 대한 백분위 점수, 표준점수, 영역별 배정 비율에 따라 가중치가 부여된 변환표준점수를 산출하여 성적을 통지하였다. 그 밖의 Kim(1998), Kim(1999), Park et al.(1998, 2000) 등도 표준점수와 관련한 연구를 수행하였다.

2005학년도 수능은 계열별 구분 없이 시험 영역과 과목을 전부 또는 일부 선택할 수 있게 되었고 기존에 통지되었던 원점수는 표기하지 않게 되었다. 이에 따라 새로운 표준점수 산출 방안에 관한 다양한 논의와 연구가 진행되었다. 탐구영역 선택과목에 따른 원점수의 차이는 과목별 난이도와 선택 집단의 학력 차이 때문에 발생한다. Hwang(2005)은 과목별 난이도는 표준점수를 통하여 보정하고 학력 차이는 과목별 평균 점수를 토대로 가산 점수를 부여해 보정한 방법을 제안하였다. Nam(2002)은 선형계획모형을 이용하여 선택과목의 학력 차이를 반영한 표준점수를 도출하였다. Nam(2011)은 기존 선형계획모형의 약점을 보완하여 2010학년도 사회탐구 선택과목에 응시한 학생의 실제 표준점수를 이용해 최적해를 구하는 연구를 수행하였다. 서로 다른 검사 결과를 비교하기 위한 동등화(equating) 및 척도화(scaling) 방법으로 점수를 조정하는 연구도 있었다(Nam, 2003; Nam, 2004). 문항반응이론(item response theory)은 문항의 난이도와 변별도를 고려해 학생의 능력점수를 산출하는 것으로 Park(2005)는 모의 자료를 생성하여 모수를 추정하고 이 방법의 타당성을 입증하였다. 다양한 논의와 연구에도 불구하고 2005학년도 수능 점수 보고체계는 선택과목 간의 점수를 조정하지 않고 각각 독립적으로 표준점수를 산출하도록 하였다.

2008학년도 수능에서는 표준점수, 백분위, 등급을 표기하지 않고 등급만을 표기하였고 이를 계기로 등급제와 관련한 연구가 있었다. Yang et al.(2006)은 안정적인 등급 산출을 위한 조건이 무엇인지 규명하였고 점수의 가지 수가 많은 경우와 다양한 수준의 문항 난이도를 갖는 경우에 등급 비율이 안정적으로 산출되었음을 보였다. 수능 등급제가 적절하지 못하다는 연구 등도 있었다(Yang, 2006; Ban, 2008).

Jin et al.(2010)은 영어와 수학의 수준별 집단에 따른 평가방안과 집단 간 공통 평가방안을 구분하여 평가지의 구성과 점수 산출 방안을 제안하였다. Yang(2012)은 2014학년도에 실시할 국어·수학·영어 영역의 수준별 수능시험에 대하여 학생, 학부모, 교사의 인식이 어떻게 차이 나는지 규명하기 위하여 로지스틱 회귀분석을 이용하여 분석하였다. Park et al.(2015)는 2004~2014학년도 영어 영역의 수능 문항 및 모의고사 문항을 대상으로 정답률을 예측할 수 있는 다중선형회귀분석을 실시하였고 CART(classification and regression tree)를 이용하여 난이도의 상·하를 구분하였다. 이때 사용된 독립변수는 텍스트 마이닝의 대표적인 분석 기법인 토픽 모델(topic model)을 이용하여 도출한 문항별 각 토픽의 빈도수와 문항별 특성을 나타낼 수 있는 다양한 지표들이었다.

2017학년도 수능부터 일부 영역에서 절대평가를 실시함에 따라 평가원은 절대평가 대상인 영역의 시험체제와 점수 체제 방안을 제안하였다(KICE, 2014; KICE, 2015). 절대평가 점수 체제는 등급 분할 방식과 등급의 수를 결정하는 것이다. 등급 분할 방식은 분할 점수를 미리 정해 놓은 고정 분할 방식과 평가 후에 문항 분석을 통하여 정하는 준거 설정 방식 등으로 구분하고 등급은 5등급 안과 9등급 안으로 구분하여 각 대안의 장단점을 제시하였다. 교육부는 최종적으로 9등급 고정 분할 방식을 채택하였다.

교육부는 2022년 하반기에 최종 확정·고시할 예정인 ‘2022 개정 교육과정’에 따라 2024년 2월에 ‘2028학년도 대학입시 개편안’을 발표할 예정이다. 주요 논점인 고교학점제 도입, 수능의 절대평가 확대 및 서·논술형 평가제 도입에 관련한 연구가 있었다. Yi(2020)은 고교학점제, 수능 절대평가와 같은 진보 교육계의 주요 정책 대안은 교육의 본질인 성취도 평가를 중시한 것이지만 대학입시의 선발 제도적 성격을 경시함으로써 성공적이지 못하다고 결론내렸다. Chang(2021)은 수능의 서·논술형 평가 도입을 정당화하고 그 방향성을 탐색한 연구를 수행하였다. 해외의 대입 서·논술형 평가 현황을 고찰하고 수능에서 측정해야 할 쓰기 능력의 본질을 밝히고 평가의 방향성을 제시하였다.

2.3 수능 점수 체제의 구성

표준점수 제도는 선택과목이 도입된 1999학년도부터 시작되었다. 그 당시 선택과목이 없는 언어, 수리·탐구Ⅰ, 외국어 영역에서 원점수(x)를 표준점수(T)로 변환하는 과정은 식(1)과 같다.

2004학년도까지는 모든 영역에서 T = 50 + 10Z로 표준점수를 계산하였는데 영역별 만점자의 표준점수는 각각 다르고 영역의 배점도 같지 않았다. 그러므로 모든 영역에서 만점을 받은 수험생의 표준점수 합도 총점과 일치하지 않았다. 이러한 문제를 해결하기 위하여 배점에 대한 가중치를 부여하고 만점자의 표준점수 합계가 총점과 일치하도록 일정한 상수를 곱하여 변환표준점수를 산출하고 이를 수험생에게 통지하였다.

2005학년도 수능부터 100점 만점 영역은 T = 100 + 20Z, 50점 만점 영역/과목은 T = 50 + 10Z로 표준점수를 계산하였다. 이때부터 종합등급은 표기하지 않았으므로 변환표준점수는 그 의미를 잃게 되어 2005학년도부터 변환표준점수는 통지하지 않고 표준점수만 통지하였다. 표준점수는 2001학년도까지는 소수 둘째 자리까지 통지하였고 2002학년도 이후에는 정수로 통지하였다.

1999학년도 수리·탐구Ⅱ 영역은 공통과목과 선택과목으로 구성되었다. 선택과목이 있는 경우 선택과목에 따른 차이를 반영하기 위하여 선택과목의 원점수를 조정하는 방식이 제안되었다. 이러한 방식은 공통과목과 선택과목이 혼합된 영역에 적용하였으며 1999~2004학년도는 탐구영역, 2005~2011학년도는 수리 영역 가형, 2022학년도는 국어와 수학 영역에 적용하였다. 선택과목의 원점수를 조정 원점수로 변환하여 표준점수를 산출하는 식은 다음 식(2)와 같다.

2022학년도 수능에서 국어는 공통과목 76점, 선택과목 24점으로 배정되었으며 수학은 공통과목 74점, 선택과목 26점으로 배정되었으므로 국어의 α는 0.76, 수학의 α는 0.74이다. x_ij는 선택과목 j에 응시한 수험생 i의 공통과목 원점수이고 y_ij는 선택과목 j에 응시한 수험생 i의 선택과목 원점수이다. y_ij는 선택과목 j의 난이도와 선택과목 j를 선택한 수험생의 수학 능력 차이를 반영하지 못한 점수로 이를 조정할 필요가 있다. yija 는 원점수 y_ij를 조정한 원점수로 yija 의 평균과 표준편차는 공통과목 원점수 x_ij의 평균(μ)과 표준편차(σ)와 같도록 변환한 것이다. yija 를 구하는 구체적인 과정은 KICE(2019)에 자세하게 설명되어 있다.

백분위는 1994학년도 수능이 시작된 이후 현재까지 수험생에게 통지되었다. 2004학년도까지는 ‘백분위점수’라는 용어를 사용하였으며 2005학년도부터는 ‘백분위’라는 용어로 변경하였다. 백분위를 구하는 기준은 원점수 및 표준변환점수에서 표준점수로 변화하였다. 총점의 백분위는 1994학년도부터 2001학년도까지, 영역별 원점수의 백분위는 1997학년도부터 2004학년도까지, 총점의 변환표준점수 및 이의 백분위는 2000학년도부터 2001학년도까지, 영역별 변환표준점수의 백분위는 2000학년도부터 2004학년도까지, 영역별 표준점수의 백분위는 2005학년도부터 2022학년도까지(2008학년도 제외) 표기하였다. 또한 백분위는 1994학년도부터 2001학년도까지는 소수 둘째 자리까지, 2002학년도 이후부터는 소수 첫째 자리에서 반올림하여 정수로 표기하였다.

백분위 산출은 동점자를 어떻게 처리하느냐에 따라 두 가지 방식으로 구분한다. 첫 번째는 자신보다 낮은 점수를 갖는 수험생 수를 백분율로 나타낸 방식으로 2004학년도 이전까지의 수능에서 사용하였다. 2001년 평가원에서 발표한 ‘대학수학능력시험 Q&A’에 의하면 백분위 점수는 계열별 전체 응시자 중 한 수험생이 얻은 점수(원점수, 변환표준점수)보다 더 낮은 점수를 얻은 수험생들의 백분율을 나타내주는 점수라고 정의하였다. 두 번째는 자신보다 낮은 표준점수를 갖는 수험생 수와 동점자 수의 반을 백분율로 나타내는 방식으로 2005학년도 이후 수능부터 사용하였다. 2004년 평가원에서 발표한 ‘2005학년도 대학수학능력시험 Q&A 자료집’에 의하면 백분위를 구하는 공식은 다음 식(3)과 같다.

등급제는 2002학년도 수능부터 실시되었다. 정규분포를 가정하여 만들어진 9등급(stanine: standard nine) 방식으로 등급은 소수 셋째 자리에서 반올림해 둘째 자리까지 산출한 변환표준점수에 의해 결정되었다. 2004학년도에는 소수 첫째 자리에서 반올림해 정수로 산출한 변환표준점수에 의해 등급을 결정하였다. 2004학년도까지는 종합영역의 등급도 표기하였지만 2005학년도부터는 종합영역의 등급은 표기하지 않고 영역/과목의 등급만 표기하였다. 이때부터 변환표준점수를 산출하지 않음에 따라 등급을 부여하는 기준으로 소수 첫째 자리에서 반올림해 정수로 산출한 표준점수를 사용하였다. 등급을 구분하는 절차는 다음과 같다(웹 사이트 ‘나무위키 수능 등급제’를 참고하여 연구자가 수정하였음).

첫째, 해당 영역/과목에 응시한 전체 응시자의 원점수 평균과 표준편차를 구한다.

둘째, 표준점수를 산출한 후 소수 첫째 자리에서 반올림하여 정수로 표기한다.

셋째, 표준점수의 점수별 도수분포표를 작성한다.

넷째, 표준점수의 점수별 누적 비율(cumulative percent)을 구한다. 누적 비율은 해당 표준점수 이상을 받은 수험생의 비율이다.

다섯째, 당해 표준점수까지의 누적 비율이 4%보다 같거나 크게 되는 최초의 표준점수가 1등급과 2등급을 구분하는 등급 구분 표준점수가 되고 이 표준점수 이상을 받은 수험생에게는 1등급을 부여한다.

여섯째, 1등급과 2등급을 구분하는 표준점수 바로 밑의 점수부터 당해 표준점수까지의 누적 비율이 11%보다 같거나 크게 되는 최초의 표준점수가 2등급과 3등급을 구분하는 등급 구분 표준점수가 되고 이 표준점수 이상을 받은 수험생까지 2등급을 부여한다.

일곱째, 이러한 방식으로 <Table 1>의 누적 비율을 반영하여 8등급까지 등급을 부여한 후 8등급과 9등급을 구분하는 표준점수 바로 밑의 점수부터 표준점수 최저점을 받은 수험생에게 최하 등급인 9등급을 부여한다.

Table 1.

Percentage (%) & Cumulative Percentage (%) by Stanine Levels

3.1 표준점수의 특성

국어 및 수학 영역과 탐구영역 과목별 표준점수의 도수분포표를 이용하여 기술 통계량을 계산해봄으로써 표준점수의 통계적 특성을 규명하였다. 표준점수의 도수분포표를 이용하여 최고점(maximum)과 최저점(minimum)의 차이인 범위(range), 평균(mean), 표준편차(standard deviation: S.D.), 중앙값(median: MED) 그리고 왜도(skewness) 및 초과첨도(excess kurtosis: E.K.)를 계산하였다. 왜도는 {E(X - μ) ³/σ³}이고 이 값이 양이면 오른쪽으로 긴꼬리(right skewed), 음이면 왼쪽으로 긴꼬리(left skewed)를 갖는다. 초과첨도(이하 첨도)는 {E(X - μ)⁴/σ⁴ - 3}이고 이 값이 양이면 정규분포보다 두꺼운 꼬리(heavy tailed), 음이면 얇은 꼬리(short tailed)를 갖는다. 2022학년도 국어 및 수학 영역과 탐구영역 과목별 표준점수의 통계적 특성은 <Table 2>와 같다.

Table 2.

Statistical Characteristics of 2022 CSAT Standard Score by Area / Subject

탐구영역 과목의 표준점수 특성을 살펴보면 표준점수의 최고점은 과목에 따라 차이가 있었다. 사회탐구 영역에서의 표준점수 최고점으로 ‘윤리와 사상’과 ‘사회·문화’는 68점으로 가장 높았으며 ‘정치와 법’은 63점으로 가장 낮았다. 과학탐구 영역에서의 최고점으로 ‘지구과학 II’는 77점으로 가장 높았으며 ‘화학 I’, ‘물리학 II’, ‘생명과학 II’는 68점으로 가장 낮았다. 직업탐구 영역에서의 최고점으로 ‘상업 경제’는 77점으로 가장 높았으며 ‘공업 일반’은 66점으로 가장 낮았다. 일반적으로 사회탐구 영역보다 과학탐구 영역의 고득점자 표준점수가 높게 나타났다. 표준점수의 범위도 과목별로 상이하게 나타났다. 사회탐구 영역 과목들의 범위는 34~40점, 과학탐구 영역 과목들의 범위는 38~48점, 직업탐구 영역 과목들의 범위는 32~51점 사이에 분포하였다.

탐구영역 표준점수의 평균과 표준편차는 각각 50점과 10점으로 정해졌으나 이 값과 약간의 차이가 발생한 이유는 소수 첫째 자리에서 반올림한 표준점수의 도수분포표로 평균과 표준편차를 계산하였기 때문이다. 왜도는 비대칭 정도를 평가하는 통계량으로 그 값이 음이면 중앙값이 평균보다 크고 양이면 중앙값이 평균보다 작게 되는데 탐구영역 모든 과목에서 이러한 관계가 성립한 것을 확인할 수 있었다. 탐구영역 모든 과목의 표준점수 첨도가 음으로 나타난 것은 평균과 많이 떨어진 점수의 도수가 정규분포보다 상대적으로 낮았음을 의미한다.

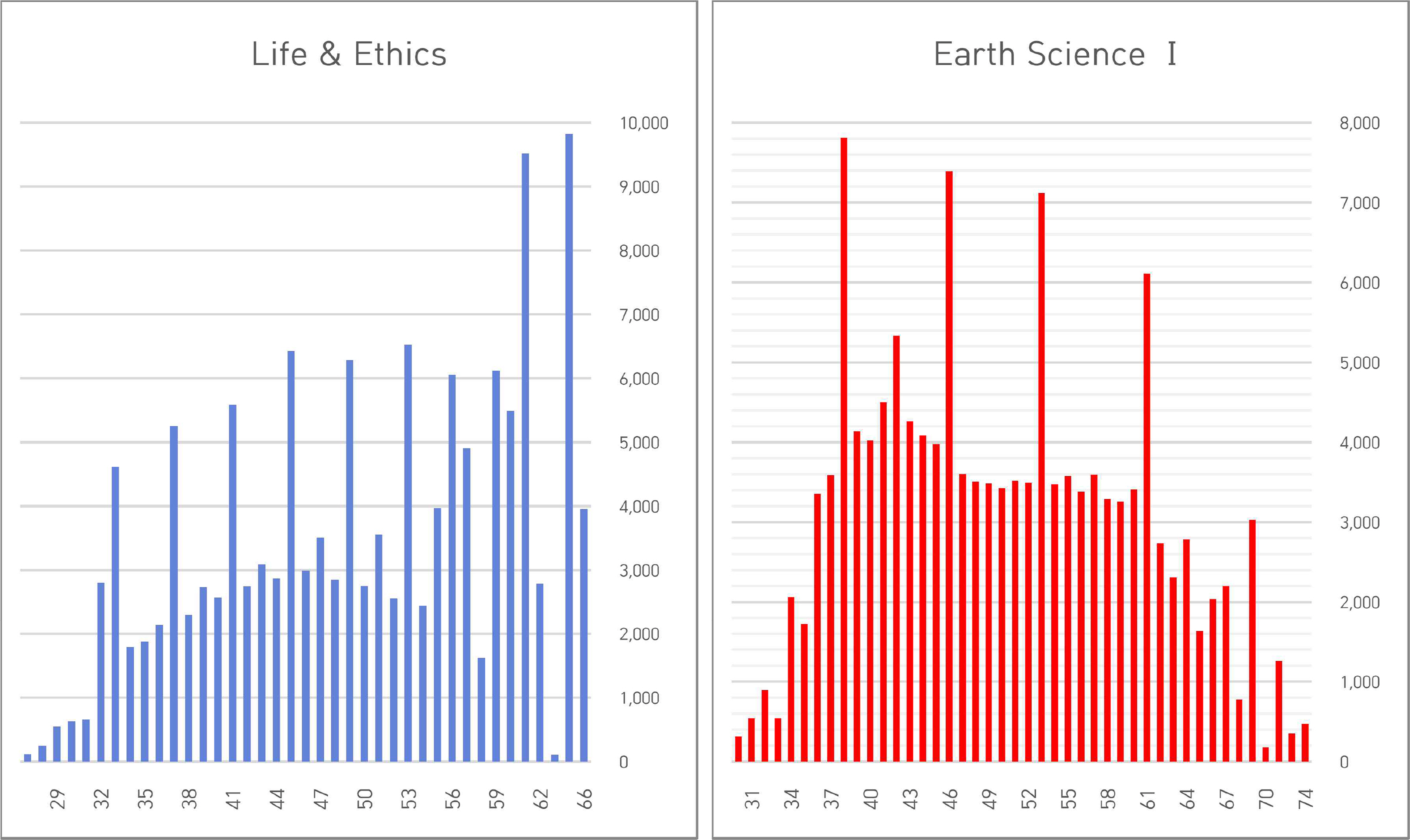
2022학년도 수능 사회탐구 영역에서 수험생이 가장 많이 선택한 과목은 ‘생활과 윤리’이고 과학탐구 영역은 ‘지구과학Ⅰ’이다. 다음의 <Figure 1>에는 ‘생활과 윤리’와 ‘지구과학Ⅰ’의 표준점수 인원수를 막대그래프로 나타내었다.

Figure 1.

Frequency of the Standard Scores for ‘Life & Ethics’ and ‘Earth Science I’

‘생활과 윤리’의 표준점수는 최고 66점, 최저 26점, 범위 40점, 평균 50.01점, 중앙값 51점, 왜도 –0.236으로 중앙값이 평균보다 크고 좌측 꼬리가 길게 나타났다. ‘지구과학Ⅰ’의 표준점수는 최고 74점, 최저 30점, 범위 44점, 평균 50.00점, 중앙값 49점, 왜도 0.227로 중앙값이 평균보다 낮고 우측 꼬리가 길게 나타났다.

이 그래프들에서 특이하게 나타난 것은 특정한 표준점수에서의 인원수가 주위 표준점수의 인원수보다 상당히 높게 나타난 것이다. 인원수가 높게 나타난 표준점수는 ‘사회와 윤리’의 경우 약 4점 간격으로, ‘지구과학Ⅰ’은 7~8점 간격으로 반복되고 있다.

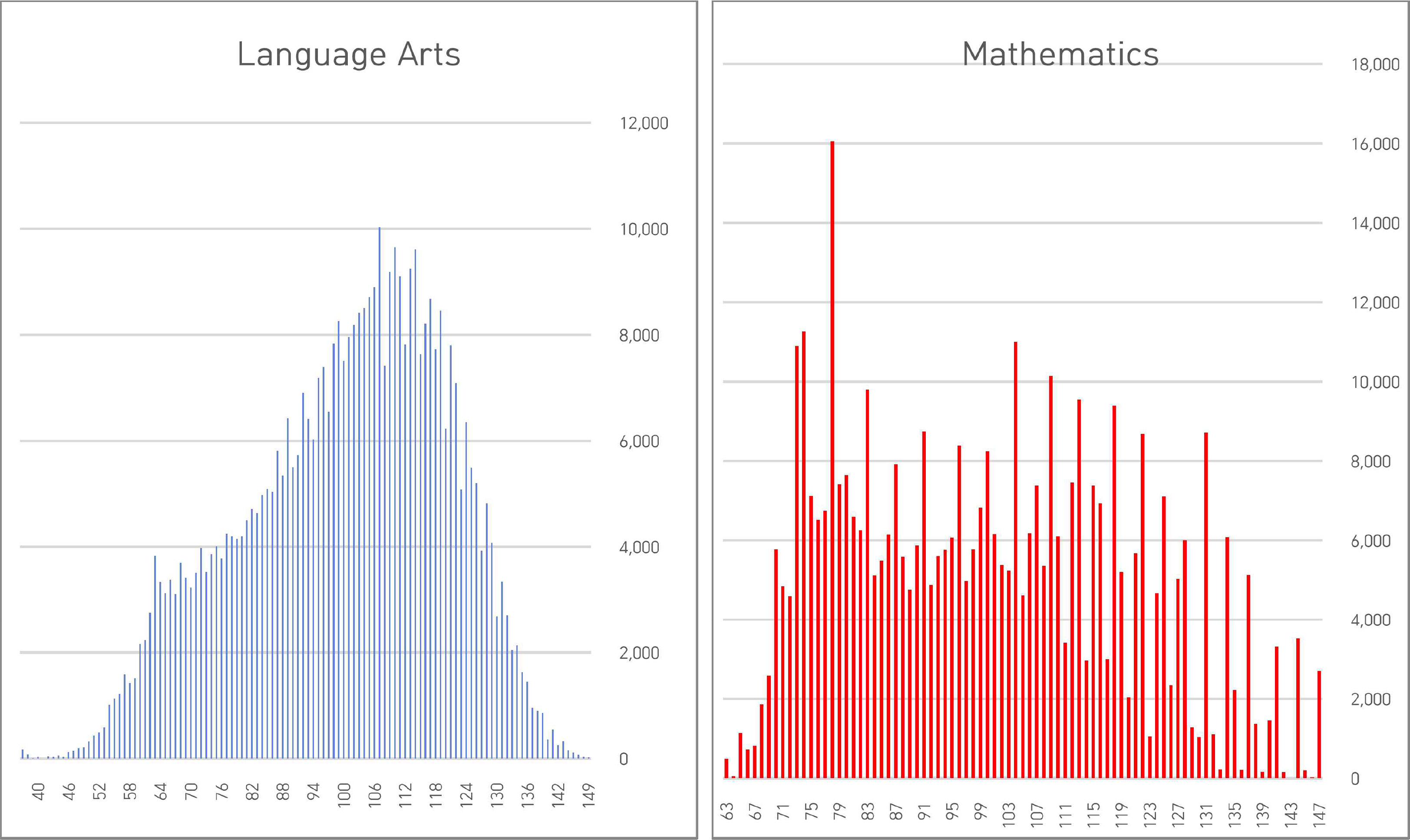
탐구영역 과목에서는 배점이 2점과 3점인 문항이 각각 10개로 가능한 원점수의 최대 가지 수는 49개이므로 표준점수도 최대 49가지가 나올 수 있다. 국어 및 수학 영역의 최소 배점도 2점으로 가능한 원점수의 최대 가지 수는 99개이다. 국어 및 수학 영역은 공통과목과 선택과목으로 구성되어 있어 원점수가 같더라도 어떤 과목을 선택했는지에 따라 표준점수가 달라지기 때문에 표준점수의 최대 가지 수는 99개를 초과할 수 있다. 국어 영역의 표준점수는 37~149점, 수학 영역은 63~147점으로 분포하고 평균과 표준편차는 100점과 20점에 거의 근사하게 나타났다. 국어는 왜도 –0.37로 왼쪽 꼬리, 수학은 왜도 0.275로 오른쪽 꼬리가 길게 나타났다. 국어와 수학 영역의 표준점수 인원수를 막대그래프로 나타내면 <Figure 2>와 같다. 그림에는 국어와 수학의 표준점수 특성들이 잘 나타나 있으며 <Figure 1>과 마찬가지로 특정 표준점수에서 주위보다 상대적으로 높은 인원수를 보여주고 있다.

Figure 2.

Frequency of the Standard Scores for ‘Language Arts’ and ‘Mathematics’

3.2 등급의 특성

2022학년도 수능에서 영역/과목별 등급 구분 표준점수와 각 등급에 해당하는 수험생의 수 및 비율 자료를 분석한 결과 <Table 1>에서 의도했던 등급별 비율과는 차이가 났다. 1등급부터 9등급까지 의도했던 누적 비율과 실제 누적 비율 간의 차이를 알아보기 위하여 다음과 같은 지표를 개발하였다. 영역/과목 k의 l등급까지의 실제 누적 비율을 Okl, l등급까지 의도했던 누적 비율을 E^l로 나타내면 영역/과목 k에서 각 등급까지 의도했던 비율보다 높게 배정된 수험생 비율을 모든 등급에서 합한 G_k는 다음 식(4)와 같다.

각 등급에 배정된 수험생 비율이 의도대로 배분되지 않을수록 이 값이 커지게 된다. 그러므로 G_k는 안정적 등급 산출을 평가할 수 있는 지표로 활용할 수 있다. 다음 <Table 3>에는 1, 3, 5, 7등급의 의도된 누적 비율(E^l), 영역/과목별 구분 표준점수와 누적 비율(Okl) 그리고 지표 G_k를 나타내었다. 국어와 수학 영역은 등급 l에서 Okl 이 E^l을 초과한 정도가 작았으며 G_k도 각각 4.25, 3.55로 탐구영역 과목에 비해 작게 나타났다. Okl 이 E^l을 가장 많이 초과한 영역/과목은 l = 1의 경우는 ‘생활과 윤리’로 6.07 초과, l = 3의 경우는 ‘수산·해운 산업 기초’로 6.03 초과, l = 5의 경우는 ‘인간 발달’로 5.46 초과, l = 7의 경우는 ‘윤리와 사상’으로 3.97 초과하였다. G_k가 가장 컸던 영역/과목은 ‘수산·해운 산업 기초’ 19.35, ‘윤리와 사상’ 19.15, ‘공업 일반’ 18.27의 순으로 나타났다.

Table 3.

Level 1, 3, 5 and 7 Cut Standard Score and Cumulative Percent by Area / Subject

다음 <Figure 3>에는 수학 영역과 사회탐구 영역 ‘윤리와 사상’에 대한 등급별 누적 비율을 그래프로 제시하였다. 모든 등급에서 ‘윤리와 사상’의 등급별 누적 비율이 수학보다 높게 나타났다.

Figure 3.

Cumulative Percent of Stanine Levels for ‘Ethics & Thoughts’ and ‘Mathematics’

4.1. 표준점수의 문제점

원점수가 표준점수로 변환되는 과정에서 원점수의 차이가 제대로 반영되지 못하는 문제는 다음과 같다. 탐구영역 과목 k의 원점수 평균과 표준편차를 μ_k , σ_k로 나타내면, 과목 k에서 원점수 x_k를 받은 수험생의 T점수 T(x_k)는 50 + 10×(x_k - μ_k)/σ_k이 된다. 원점수 (x_k + 1)과 x_k의 표준점수 차이 T(x_k + 1)- T(x_k)는 10/σ_k이다. 즉, σ_k가 클수록 원점수 1점 차이로 인한 표준점수 차이는 작아진다. σ_k가 10보다 크면 T(x_k + 1)- T(x_k)는 1보다 작아지며, σ_k가 10보다 작으면 T(x_k + 1)- T(x_k)는 1보다 크게 된다. 평가원에서 발표한 원점수 x_k를 받은 수험생의 표준점수는 T(x_k)가 아니고 이를 소수점 첫째 자리에서 반올림하여 정수로 나타낸 값으로 이를 구분하기 위하여 정수화된 표준점수를 TI(x_k)로 나타내면 다음과 같이 식(5)의 부등식이 성립한다.

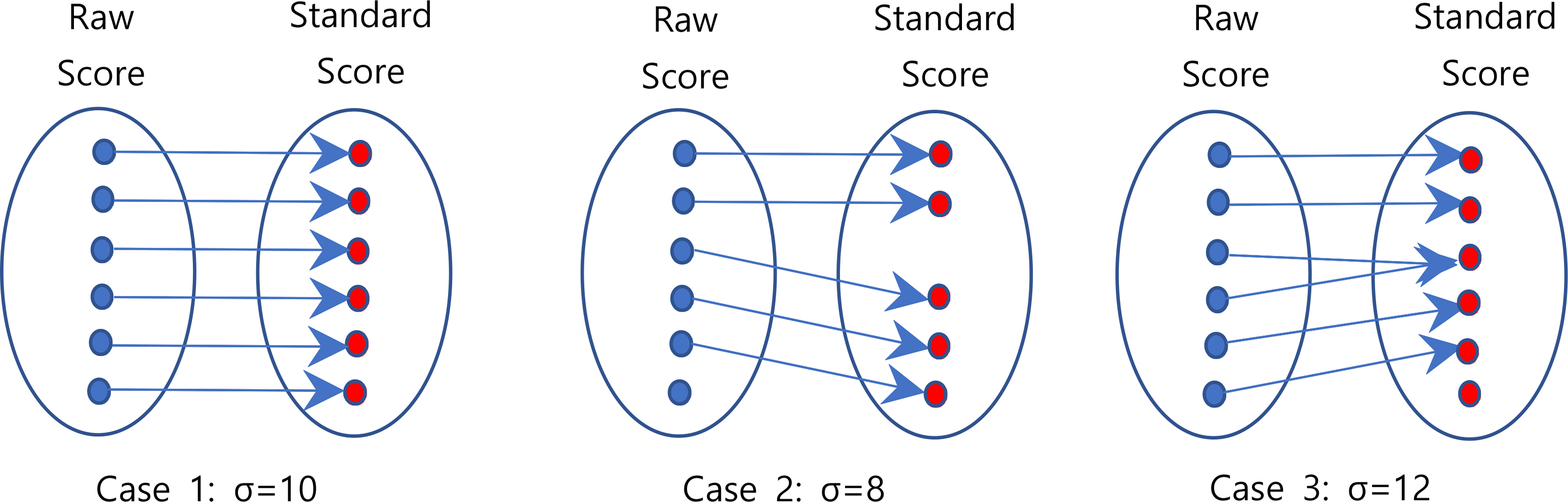
본 논문에서는 ‘정수화되기 전의 표준점수’를 ‘T’로, ‘정수화된 표준점수’를 ‘TI’로 표시하여 서술하였다. 탐구영역 과목의 가능한 원점수 x의 집합을 X라고 정의하면 X = {0, 2, 3, ... , 47, 48, 50}이 된다. 과목 k에서 실제로 나온 원점수 x_k의 집합을 Xk로 정의하면 X k ⊂ X가 성립한다. TI의 가능한 점수 집합은 과목 k에 따라 차이가 있으며 이를 Y_k로 정의한다. 과목 k에서 집합 X k의 원소 개수를 mk, 집합 Y_k의 원소 개수를 n_k라고 나타내면 mk와 n_k의 비율 (mk : n_k)는 σ_k와 관계가 있다. 다음 <Figure 4>에는 σ_k의 크기에 따른 (mk : n_k)의 관계를 나타내었다.

Figure 4.

Relationship between the Raw Score and the Standard Score(TI) according to the Standard Deviation

사례 1은 σ(표준편차)가 10인 경우로 원점수 1점 차이는 T 및 TI의 1점 차이가 되어 m : n (m = n)의 관계가 성립한다. 사례 2는 σ가 8인 경우로 원점수 1점 차이는 T의 1.25점 차이가 난다. 이 경우 원점수 1점 차이가 TI 2점 차이로 나오는 경우가 발생하며 이러한 현상은 원점수 4점에 한 번씩 발생한다. σ가 10보다 작은 경우에는 m : n (m = n)의 관계가 성립하며 원점수 1점 차이가 TI 2점 차이로 나오는 현상이 발생한다. 사례 3은 σ가 12인 경우로 원점수 1점 차이는 T의 5/6점 차이가 되어 (6 : 5)의 관계가 성립한다. 이 경우 원점수 1점 차이가 TI 0점 차이로 나오는 경우가 발생하며 이러한 현상은 원점수 6점에 한 번씩 발생한다. σ가 10보다 큰 경우에는 m : n (m > n)의 관계가 성립하며 원점수 1점 차이가 TI 0점 차이로 나오는 현상이 발생한다.

탐구영역 과목 중 ‘생활과 윤리’, ‘지구과학Ⅰ’ 그리고 ‘성공적인 직업생활’의 수리적 예시를 통해 이 과목들이 위의 사례 중 어디에 해당하는지 다음과 같이 살펴보았다. 세 과목이 어느 사례에 해당하는지 파악하기 위하여서는 σ_k의 값을 알아야 하지만, 평가원에서는 원점수의 평균이나 표준편차를 공개하지 않으므로 알 수 없다. 그러므로 평가원에서 발표한 TI 도수분포표를 통해 σ_k를 추정할 필요가 있다. 탐구영역 과목에서 만점 50점을 받은 수험생과 0점을 받은 수험생이 적어도 한 명은 존재할 것이라 가정하는 것은 큰 무리가 없을 것이다. 2022학년도 생명과학Ⅱ는 20번 문항 출제 오류로 인하여 전원 정답처리 하였으므로 원점수 최저점은 2점이었지만 이것은 예외적인 사항이었다. 탐구영역 과목 k의 원점수 최고점을 50점, 최저점은 0점으로 가정하여 σ_k를 추정하는 방법은 다음과 같다.

평가원에서 발표한 과목 k의 TI 최고점 TIkH 와 최저점 TIkL 의 차이인 범위 (TIkH-TIkH)를 이용하여 σ_k는 식(6)과 같이 구간을 추정할 수 있다.

<Table 2>에서 ‘생활과 윤리’와 ‘지구과학Ⅰ’ 과목의 범위는 각각 40과 44이고 식(6)을 이용하면 ‘생활과 윤리’의 표준편차는 (12.20, 12.82), ‘지구과학Ⅰ’의 표준편차는 (11.11, 11.63) 구간에 속하게 된다. 따라서 ‘생활과 윤리’의 원점수 1점 차이는 (0.78, 0.82)의 T 차이, ‘지구과학Ⅰ’의 원점수 1점 차이는 (0.86, 0.9)의 T 차이가 나타나 두 과목은 모두 사례 3에 해당한다. T 차이는 n : m의 비율로 나타낼 수 있으며 ‘생활과 윤리’의 T 차이가 0.8이면 (m : n = 5 : 4), ‘지구과학Ⅰ’의 T 차이가 0.9이면 (m : n = 10 : 9)이 된다. 즉 ‘생활과 윤리’에서 ‘지구과학Ⅰ’에 비해 더 짧은 간격으로 반복해서 두 개의 원점수가 하나의 TI로 나타난다. 이것은 <Figure 1>에서 ‘생활과 윤리’는 표준점수 4점 간격, ‘지구과학Ⅰ’은 표준점수 7~8점 간격으로 인원수가 높게 나타난 이유를 설명할 수 있는 하나의 근거가 될 수 있다. 특정 TI대의 인원수가 높게 나온 현상은 두 개의 원점수가 하나의 표준점수로 계산된다는 이유 외에도 문항별 난이도, 수험생이 특정 원점수를 받을 확률의 차이 등의 이유도 가능하다.

직업영역 ‘성공적인 직업생활’은 TI 범위가 51로서 탐구영역 과목 중 가장 높았다. 표준편차는 (9.23, 9.60) 구간, 원점수 1점 차이는 (1.04, 1.08)의 T 차이가 남에 따라 사례 2에 해당한다. T 차이가 1.06이면 (m = n)이지만, 원점수 1점 차이가 TI 2점 차이로 나타날 수 있다. 실제로 ‘성공적인 직업생활’의 표준점수 도수분포표에 표준점수 43점은 없고 44점과 42점만 있는 것을 확인할 수 있었다. 표준점수를 정수화하는 과정에서 원점수 1점 차이가 표준점수 0점 또는 2점 차이로 발생할 수 있다는 사실은 Hwang(2005)의 연구에서도 지적하였다. 본 연구에서는 이러한 현상이 발생하는 이유를 표준편차의 크기에 따라 이론적으로 설명하였다.

4.2 백분위 및 등급의 문제점

백분위와 등급은 같은 과목을 응시한 수험생의 상대적 위치를 평가하기 위하여 도입한 것으로서 원점수를 최대로 반영하여 산출하는 것이 바람직하다. 왜냐하면 한 과목의 수학 능력을 측정하기 위하여 신뢰도와 타당도가 입증된 시험문제를 출제하였고 이를 평가한 결과가 원점수이기 때문이다. 현재 TI 기준으로 산출한 백분위 및 등급이 원점수 기준으로 산출한 백분위 및 등급과 어떤 차이가 발생하는지 다음과 같이 살펴보았다.

평가원에서 발표한 탐구영역 과목 k의 TI 분포표를 이용하여 특정 TI의 백분위 및 등급을 산출하는 방법은 앞의 2.3에서 설명하였다. 현재는 원점수의 도수분포표를 발표하지 않으므로 원점수 기준의 백분위 및 등급을 산출할 수 없다. TI 및 원점수 기준으로 산출한 백분위 및 등급의 차이를 비교하려면 원점수의 도수분포표를 알아야 한다. 본 연구에서는 탐구영역 ‘생활과 윤리’ 과목의 원점수 도수분포표를 다음의 가정을 통해 도출하였다.

가정 1: ‘생활과 윤리’의 원점수 평균 μ_k = 29.86, 표준편차 σ_k = 12.61

가정 2: TI(x_k) = TI(x_k + 1)이면 원점수 x_k와 (x_k + 1)을 받은 수험생의 인원수는 같음

입시 전문학원 ‘M’ 및 ‘J’에서는 2022 수능 영역/과목별 등급 구분 표준점수(TI)와 이에 해당하는 원점수를 공개하였다(Megastudy, 2021; Jongro Academy, 2021). 두 입시 전문학원에서 공개한 ‘생활과 윤리’의 등급 구분 원점수는 같았으며 본 연구에서도 같은 결과가 나오도록 가정 1을 하였다. 가정 1과 2는 수리적 예시의 설명을 위하여 설정한 것으로 실제와는 다르다. <Table 4>에는 TI별 인원수, TI기준으로 산출한 백분위, 누적 비율, 등급과 원점수별 인원수, 원점수 기준으로 산출한 백분위, 누적 비율, 등급을 나타내었다.

Table 4.

Percentile, Cumulative Percent and Level Based on the Standard Score and the Raw Score

2022학년도 수능 ‘생활과 윤리’에 응시한 수험생은 총 136,793명으로 탐구영역 과목 중 가장 많았다. ‘생활과 윤리’에서 원점수와 TI의 m : n = 49 : 39이다. 즉, 원점수 49가지가 TI 39가지로 변환하였고 원점수 2개가 TI 1개로 변환한 경우는 10번이었다. <Table 4>에서 이러한 부분은 칸에 명암을 주어 진하게 나타내었다. 원점수와 TI 기준의 백분위 및 등급은 이처럼 진하게 표시된 10곳에서 차이가 났으며 나머지 29곳에서는 원점수와 TI 기준의 백분위 및 등급은 같았다. 백분위는 진하게 표시된 10곳 모두에서 차이가 날 수 있으나 백분위를 정수화하는 과정에서 일부 차이가 없는 곳도 있었다. 등급의 차이도 진하게 표시된 10곳에서 발생할 수 있으며 모든 수험생의 TI 기준 등급은 원점수 기준 등급과 비교했을 때 항상 높게 나온다. 그 이유는 앞에서 설명한 등급 산정 방식 때문이다.

예를 들어 원점수 47점과 48점의 T는 63.6점, 64.4점으로 TI는 64점이고 TI 기준 백분위는 94에 1등급이다. 원점수 기준으로 등급과 백분위를 산출하면 원점수 47점은 백분위 92에 2등급이고 원점수 48점은 백분위 95에 1등급이다. 원점수 47점을 받은 수험생은 TI로 백분위 및 등급을 산출함에 따라 원점수로 백분위 및 등급을 산출한 것보다 백분위에서 2 상향, 2등급에서 1등급으로 이득을 보았다. 원점수 48점을 받은 수험생은 백분위에서 1 하향되는 손해를 보았고 등급은 차이가 없었다. 원점수 48점을 받은 수험생은 1등급으로 등급의 차이는 없었더라도 같은 등급을 받은 수험생의 수가 많아짐에 따라 상대적으로 손해를 본 것이다.

모든 수험생은 원점수 기준으로 산정할 때보다 TI 기준으로 등급을 산정하면 더 높은 등급을 받게 되므로 안정적 등급 산출을 평가하기 위하여 개발한 지표 G_k는 원점수보다 TI에서 더 높다. 다음 <Table 5>에는 ‘생활과 윤리’ 과목의 TI 및 원점수 기준으로 산정한 등급 구분점수, 각 등급에 해당하는 인원수 및 비율 그리고 누적 인원수 비율을 나타내었다.

Table 5.

The Differences of Level Characteristics Based on the Standard Score and the Raw Score

‘생활과 윤리’에서 TI 기준 1등급 수험생은 13,769명으로 원점수 기준 1등급 수험생 8,860명보다 4,909명 많았다. 원점수 기준은 2등급이지만 TI 기준으로 1등급이 된 대상자는 <Table 4>에서 원점수 47점을 받은 수험생 4,909명이다. 또한 TI 기준 6등급 수험생은 23,707명으로 원점수 기준 6등급 수험생 20,914명보다 2,793명 많았다. 원점수 기준은 7등급이지만 TI 기준으로 6등급이 된 대상자는 <Table 4>에서 원점수 18점을 받은 수험생 2,793명이다. 그러므로 ‘생활과 윤리’를 선택한 136,793명 중 7,702명(5.63%)의 수험생이 원점수 기준에 비해 한 등급 이득을 보았다. 과목 ‘생활과 윤리’에서 TI 기준으로 산출한 등급의 G_k는 <Table 3>에서 14.88이었다. <Table 5>에서 원점수 기준으로 산출한 등급의 G_k를 계산하면 9.55가 나온다. 원점수 기준의 G_k는 TI 기준의 G_k보다 5.63 감소하였으며 이것은 5.63%의 수험생이 한 등급 상향된 위의 결과와 같다. ‘생활과 윤리’의 경우 원점수 기준으로 등급을 산출하면 G_k가 감소하였으며 TI 기준으로 등급을 산출하는 것보다 원점수 기준으로 등급을 산출하는 것이 공정한 평가라는 사실을 수리적으로 확인하였다.

탐구영역 과목 k의 원점수 집합 X k에서 TI의 집합Y_k로 변환하는 관계에서 (mk ≥ n_k)의 관계가 성립하므로 원점수 기준으로 등급을 산출하면 G_k가 감소할 가능성이 있다. 그러므로 탐구영역 모든 과목에서 원점수 기준으로 등급을 산출하는 것이 현행 TI 기준으로 등급을 산출하는 것보다 안정적이고 공정한 평가라 할 수 있다.

5.1 표준점수 및 백분위의 소수점 표기

첫 번째, 표준점수의 정수 표기를 폐지하고 소수점 표기로 변경하는 방안이다. 1999학년도에 표준점수를 도입한 이후 2001학년도까지 소수점 둘째 자리까지 표기하였으나 2002학년도부터 소수점 첫째 자리에서 반올림하여 정수로 표기하였다. 그 당시 평가원은 비교육적이고 정책적 취지에도 어긋난다고 설명하였으나 이러한 이유가 정시모집이 확대되는 현재의 수능에도 정당할지는 의문이다. 표준점수를 정수화함에 따라 <Figure 1>에서 보듯이 표준점수의 분포는 특정 점수에서 인원수가 상대적으로 높게 나타난 현상이 반복적으로 발생한다. 원점수 1점 차이가 표준점수에 반영되지 않는 경우가 발생할 수 있고 이로 인해 백분위가 상향되거나 하향되고 등급이 상향되는 문제점도 살펴보았다. 표준점수의 정수화로 인해 일부 학생에게는 심각한 손해를, 일부 학생에게는 지나친 이득을 초래할 수 있다. 그러므로 표준점수를 소수점 첫째 자리나 둘째 자리까지 표기하는 것이 바람직하다. 그렇게 되면 표준점수 분포에서 특정 점수의 인원수가 반복적으로 발생하는 현상, 1점의 원점수 차이가 표준점수에서 0점이나 2점 차이로 발생하는 문제, 수험생의 상대적 위치를 정확하게 반영할 수 있는 백분위의 산출, 안정적인 등급 산출을 기대할 수 있다.

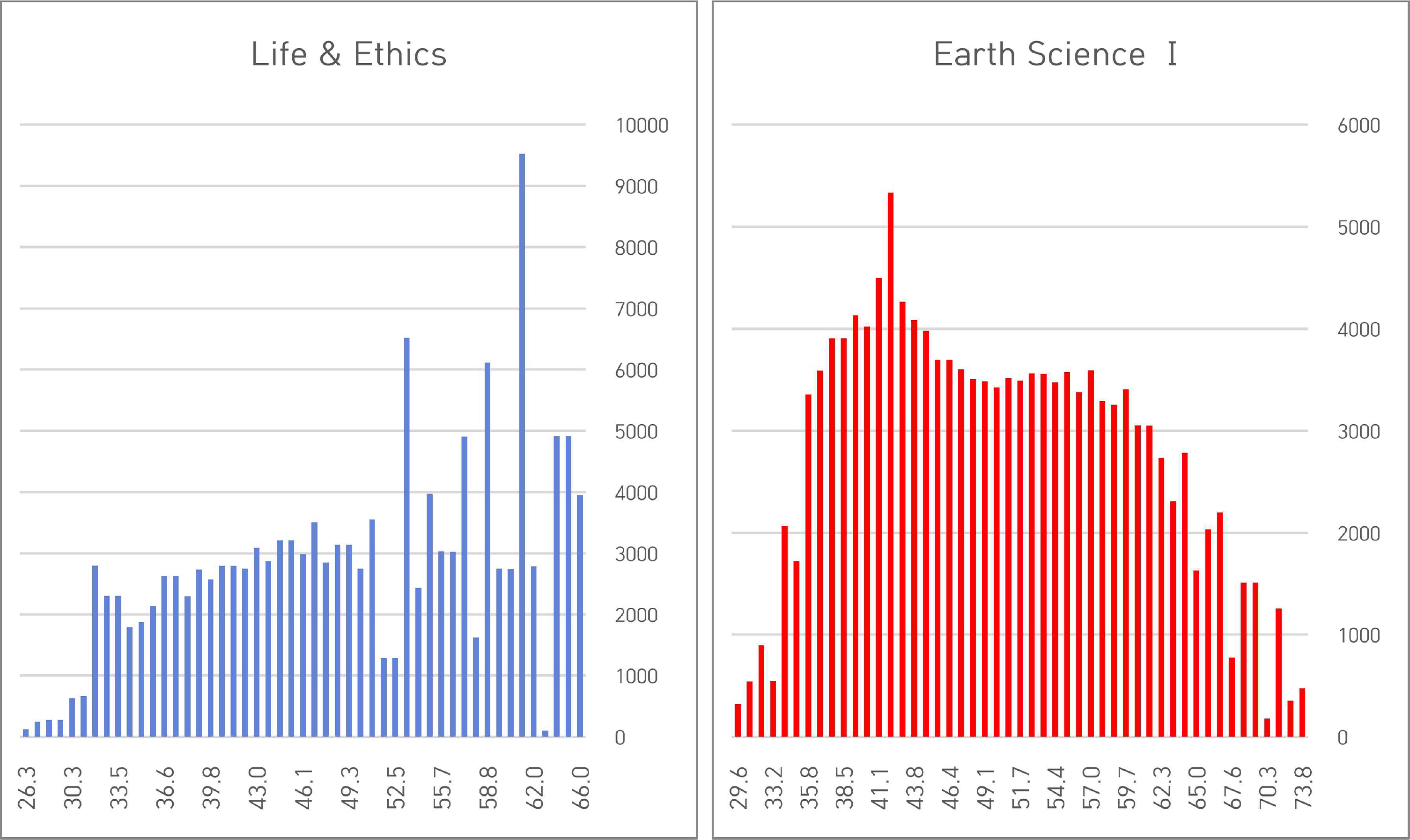
표준점수를 소수점으로 표기하였을 때 기대되는 효과 중 분포 모양의 변화를 살펴보았다. 다음 <Figure 5>에 ‘생활과 윤리’와 ‘지구과학Ⅰ’에서 소수점 첫째 자리까지 나타낸 표준점수의 인원수를 막대그래프로 나타내었다.

Figure 5.

Frequency of the Standard Scores(T) for ‘Life & Ethics’ and ‘Earth Science I’

두 번째, 백분위도 소수점 첫째 자리나 둘째 자리까지 표기하는 방안이다. 백분위를 정수로 표기함에 따라 표준점수가 다르더라도 같은 백분위가 나오고 같은 백분위라도 등급이 다르게 나오는 경우가 발생할 수 있다. ‘지구과학Ⅰ’ 의 TI가 74점(원점수 50점)인 경우와 72점(원점수 48점)인 경우 백분위는 100으로 같았다, 만일 소수점 첫째 자리까지 표기한다면 TI가 74점인 경우 백분위는 99.8, 72점인 경우 백분위는 99.5로 다르게 나타난다. 만점을 받은 수험생과 2점 배점의 문항 하나를 틀린 수험생에게 같은 백분위 결과를 제시하는 것은 공정한 평가라고 할 수 없다.

5.2 산출과정의 규정화 및 공개

표준점수, 백분위, 등급이 산출되는 과정을 구체적으로 규정하고 공개적으로 발표하는 방안이다. ‘2005학년도 대학입학전형기본계획 위헌확인’ 소송이 제기된 것은 평가원에서 구체적인 표준점수와 백분위의 산출 방법을 규정하지 않았기 때문이었다. 평가원에서 발표한 ‘2022학년도 대학수학능력시험 Q&A 자료집’(KICE, 2021)의 ‘Ⅱ 성적 및 점수 체제’를 살펴보고 아직도 명확하게 규정되어 있지 않은 두 가지 사례를 제시하였다.

첫 번째는 표준점수 산출과정 설명에서 “원점수의 평균과 표준편차를 통해 Z점수를 구한다”로 서술하였으나 평균과 표준편차를 소수점 몇째 자리까지 구한 것인지에 대한 구체적 제시가 없었던 사례이다. 예를 들어 특정 과목의 원점수 평균을 29.255점, 표준편차를 12.355점으로 산출한 원점수 41점의 표준점수는 60점이다. 만일 평균과 표준편차를 소수점 둘째 자리에서 반올림하여 평균 29.26점, 표준편차 12.36점으로 산출하면 원점수 41점의 표준점수는 59점이다. 그러므로 평균과 표준편차를 소수점 몇째 자리까지 구하여 표준점수를 산출하는지 정확하게 밝힐 필요가 있다.

두 번째는 등급 산출과정 설명에서 “전체 수험생의 상위 4%까지를 1등급으로 한다. 그다음 7%까지를 2등급으로 구분한다. 등급 구분점수에 놓여 있는 동점자에게는 해당하는 등급 중 상위 등급을 부여한다”로 서술한 사례이다. ‘2022학년도 대학수학능력시험 시행기본계획’에는 위의 설명 마지막 부분을 “동점자 발생으로 기준 비율을 초과하는 경우 상위의 등급을 부여함”으로 서술하고 있다. 이와 같은 설명은 여러 가지 해석이 가능하다. 본 연구에서는 상위 4%까지와 동점자 상위 등급의 의미를 표준점수의 누적 비율이 최초로 4보다 같거나 큰 것으로 해석하였다. 따라서 누적 비율을 구하는 과정에서 소수점 몇째 자리까지 산출할 것인지가 중요하다. 등급을 규정하기 위하여 특정 표준점수 t의 누적 비율(표준점수 t 이상을 받은 수험생의 비율)을 산출하여 이 값이 등급 l을 구분하는 E^l보다 최초로 같거나 컸는지 판단해야 한다. 표준점수 t의 누적 비율을 소수점 몇째 자리까지 산출하느냐에 따라 다음과 같은 경우가 발생할 수 있다. 소수점 둘째 자리까지 구한 표준점수 t의 누적 비율은 40.00이다. 이 값은 등급 4를 구분하는 E⁴ = 40과 같으므로 표준점수 t를 받은 수험생은 4등급이 되고 표준점수 t의 바로 아래 표준점수를 받은 수험생부터 5등급이 된다. 만일 소수점 셋째 자리까지 구한 표준점수 t의 누적 비율이 40.004이라고 하면 위의 결과와 같이 표준점수 t를 받은 수험생은 4등급이 되고 표준점수 t의 바로 아래 표준점수를 받은 수험생부터 5등급이 된다. 반면에 표준점수 t의 누적 비율이 39.995이라면 표준점수 t의 아래 표준점수를 받은 수험생까지 4등급이 된다. 그러므로 표준점수 t의 누적 비율을 소수점 몇째 자리까지 구하였는지에 따라 같은 표준점수를 받았더라도 등급은 다르게 나타날 수 있다. 또한 등급 산출의 다른 방법도 가능하다. 즉 E^l과 과목 k에 응시한 수험생 전체의 수를 곱하여 등급 l까지의 이론적 수험생 수를 계산하고 과목 k의 표준점수별 실제 누적 수험생 수와 그 크기를 비교하여 등급을 부여하는 방법이다. 이런 방법으로 계산하더라도 소수점으로 계산되는 등급 l까지의 이론적 수험생 수를 올림이나 내림으로 할 것인지, 아니면 반올림으로 할 것인지가 명확해야 한다.

5.3 공개 정보의 확대

수능 점수와 관련해 지금보다 더 많은 정보를 공개하는 방안이다. 평가원은 원점수를 공개하지 않는 이유로 원점수로는 영역/과목 간 난이도의 차이로 인해 발생하는 문제를 해결할 수 없기 때문이라고 설명하고 있다. 원점수는 시험 총점과 대비하여 몇 점을 받았는가 하는 정보만을 나타낼 뿐 개인 간 상대적인 비교나 개인 내 영역/과목 간 비교는 어렵다는 이유이다. 현재 평가원에서 공개하는 자료는 원점수에 대한 정보 없이 영역/과목별 정수로 된 표준점수 도수분포표와 등급 구분 표준점수 엑셀 파일이다. 영역/과목별 표준점수를 산출할 때 필요한 정보인 영역/과목별 원점수의 평균과 표준편차는 공개하지 않고 있다. 본 연구에서도 제한된 자료를 이용하게 됨에 따라 몇 가지 가정을 통하여 원하는 결과를 추정하였다. 그런 이유로 본 연구에서 분석한 예제 중의 일부는 실제 결과와 다를 수 있다. 대학입시 전문기관에서는 수험생이 제공하는 원점수를 바탕으로 통계 시스템을 구축하여 평가원에서 발표하지 않은 모수들을 추정하여 발표하고 있다. 평가원에서 원점수를 공개하지 않아도 일부 학생/학부모는 경제적 부담을 감수하면서 대학입시 의사결정에 필요한 정보나 조언을 듣는 경우가 있다.

2010년에 연구자에 한정하여 국가 수능 점수를 공개할 수 있도록 대법원판결(공 2010상, 663) 및 국가정책이 정해졌다(Nam, 2011). 교육부는 EDSS(EduData Service System)을 통해 연구자나 기관이 학술연구 목적으로 자료를 요청하면 심사를 거쳐 교육 관련 자료를 제공하고 있다. EDSS는 수능과 관련한 자료를 학교 단위와 개인 단위로 구분하여 제공하고 있으며 제공 항목은 표준점수, 백분위, 등급이다. 수능 점수자료를 체계적으로 분석하여 현행 점수 체제의 문제점을 도출하고 개선방안을 제안한 연구는 지금까지 활발하게 진행되고 있지 않은 실정이다. 그 이유는 연구에 필요한 원점수에 대한 정보가 공개되지 않았기 때문이다.

Seo et al.(2021)은 품질 4.0의 핵심 요소 중의 하나로 ‘데이터 획득 및 분석기술’을 도출하였다. 평가원은 수능과 관련한 점수 데이터를 공개함으로써 다양한 분야의 전문가들이 고급 분석 기법을 이용해 수능 데이터를 분석할 수 있도록 해야 한다. 2024년에 발표할 ‘2028학년도 대학입시 개편안’에는 수능에서 서·논술형 평가의 도입을 검토하고 있다. 서·논술형 수능의 가장 큰 문제 중의 하나는 채점과 관련한 것이다. Seong et al.(2022)는 기업의 외부감사 자료로부터 기계학습 방법을 통해 그룹을 구분하고 그룹별 차이를 결정짓는 핵심 어휘를 찾기 위해 텍스트 마이닝 방법을 사용하였다. 교육 기관들은 학생들이 작성한 서·논술형 문제의 답안지와 채점 결과를 공개함으로써 많은 연구자가 서·논술형 평가의 채점에 가장 적합한 비정형화된 데이터의 분석 방법을 연구할 수 있도록 권장해야 한다. 품질경영 전문가들도 이렇게 공개되는 자료를 이용하여 한국 사회에 커다란 영향을 미치는 수능 점수 체제 및 공정한 채점과 관련한 연구를 수행하여 수능 점수의 품질을 제고하길 기대한다.