계층분석방법 및 객관적평가법을 활용한 폭발물탐지장비 시험순서 최적화 방법에 관한 연구
A Study on the Method of Optimizing the Test Order of Explosive Detection System Using Analytic Hierarchy Process and Objective Rating
Article information
Trans Abstract
Purpose
As improving the search performance of aviation security equipment is considered essential, this study proposes the need for research on how to find an optimized test sequence that can reduce test time and operator power during the search function test of explosive detection systems. We derive the weights and work difficulty adjustment factor required to find the optimized test order.
Methods
First, after setting the test factors, the time of each test and the difficulty scale determined by the worker who performed the test directly were used to derive weights. Second, the work difficulty adjustment coefficient was determined by combining the basic weight adjustment factor and corresponding to the body part used by the test using objective rating. Then the final standard time was derived by calculating the additional weights for the changeability of the test factors.
Results
The order in which the final standard time is minimized when 50 tests are performed was defined as the optimized order. 50 tests should be conducted without duplication and the optimal order of tests was obtained when compared to previously numbered tests. As a result of minimizing the total standard time by using Excel's solver parameters, it was reduced by 379.14 seconds, about 6.32 minutes.
Conclusion
We tried to express it in mathematical formulas to propose a method for setting an optimized test sequence even when testing is performed on other aviation security equipment. As a result, the optimal test order was derived from the operator's point of view, and it was demonstrated by minimizing the total standard time.
1. 연구 목표 및 배경
911테러 이후 미국에서는 세계의 범죄자들과 테러리스트들로부터 시민의 안전을 확보하기 위해 국토안보부(DHS: United States Department of Homeland Security)를 창설하였다(Eum 2018). 이후 미국은 교통보안청(TSA: Transport Security Administration)을 설치하여 항공보안장비 성능 인증제를 도입하였다. 911테러와 관련 있는 항공보안장비 성능 인증제는 미국 정부가 인증하는 제도로, 공항 여객과 화물에서 사용하는 보안 검색 장비의 성능을 인증한다. 현재 미국 공항에서는 이러한 항공보안장비 성능 인증을 받은 보안 검색 장비만을 사용할 수 있다(Jung et al., 2020).
2018년부터 우리나라 또한 항공보안장비 성능 인증제를 시행하고 있다. 항공보안법 일부를 개정하면서 항공보안장비 성능 인증제의 제도적 기반을 마련하였고, 개정된 법령에 따라 한국산업기술시험원이 항공보안장비에 대해 성능시험평가기관으로 지정받으며 2019년부터 본격적으로 항공보안장비 성능 인증제가 적용되었다. 이처럼 여러 국가는 보안장비에 대한 성능 인증을 시행하고 있으며, 성능 인증을 요구하는 장비는 총 8종으로 장비에 적용되는 검색기술과 검색 대상에 따라 구분된다. 8종 장비는 엑스선검색장비(X-ray Screening System), 문형금속탐지장비(Walk-Through Metal Detector), 휴대용금속탐지장비(Hand-Held Metal Detector), 신발검색장비(Shoe Metal Detector), 폭발물탐지장비(EDS: Explosive Detecting System), 폭발물흔적탐지장비(Explosive Trace Detector), 액체폭발물탐지장비(Bottled Liquid Scanner), 원형검색장비(Whole Body Scanner)가 주로 사용되고 있다(Lee et al. 2021).
이처럼 8종 항공보안장비의 검색 성능을 향상하는 것은 필수적으로 보인다. 이를 위해 항공보안장비의 검색기능이 정확한지 확인하도록 관련 시험을 수행하는 과정에서 작업시간을 단축하고 작업자의 힘을 절감할 수 있는 최적화된 시험순서를 찾는 방법에 관한 연구의 필요성이 제기된다. 본 연구는 8종 장비 중 폭발물탐지장비를 대상으로 하는 시험을 수행하였고, 다른 장비를 대상으로 할 경우에도 최적화된 시험순서를 설정하는 방법을 제안하기 위해 수리식으로 표현하고자 한다. 연구 과정을 요약하면, 1차로 계층분석방법(AHP: Analytic Hierarchy Process)을 활용하여 시험요인의 난이도에 따른 가중치를 부여하고, 2차로 객관적 평가(OR: Objective Rating)를 활용하여 사용한 신체 부위와 시험요인 변경 여부에 따른 추가 가중치를 부여하여 최종적인 표준시간을 도출한다.
이에 따른 논문의 구성은 다음과 같다. 2장에서는 시험에 활용되는 계층분석방법 및 표준시간 선정과 관련된 개념 및 선행연구의 동향을 소개하고 3장에서는 본 연구에서 제안하는 폭발물탐지장비의 검색기능 시험순서를 최적화하는 방법을 제안한다. 4장에서는 실험분석 및 결과, 5장에서는 결론 및 추후연구 과제를 제시한다.
2. 관련 문헌 연구
2.1 최적의 시험순서 도출에 관한 연구
포병부대의 계획 표적 사격순서 결정문제(Fire Sequencing Problem with planned target for field artillery)는 산업현장에서 일어나는 제조공정 시스템의 일정계획문제(job sequencing problem)로 생각할 수 있다. 제조공정의 기계는 사격부대의 화포로, 일은 표적이라고 볼 수 있다. 보통 생산현장에서 일어나는 일정계획은 하나의 기계가 하나의 일을 할 때, 총 처리시간을 최소화하거나 평균 흐름 시간(Mean Flow Time)을 최소화하는 문제에 관하여 연구하였다(Kwon et al., 1997).
다수 표적의 수리적 모델을 활용하여 사격순서를 정하고, 사격 종료 시각을 최소화함으로써 작전 운영의 융통성을 부여해 줄 방법을 제시하였다. 또한, 야전 포병부대에서 화력계획 작성 시에 고려하는 지휘관의 의도, 포병부대의 예상되는 사격 제한, 화력계획의 차후 변경, 우선순위 표적 등 각종 실질적 상황을 고려하여 최대한 이른 시간에 사격을 마칠 수 있도록 하였다. 이와 같은 사격순서 결정문제를 혼합정수계획모형(MIP: Mixed Integer Programming)으로 구성하였고, 분석 수단으로 ILOG OPL을 이용하여 최적해를 구하였다(Hwang and Lee, 2007).
유휴시간 활용방안에 관한 연구로 예상 가능한 사격 불가능 시간을 알맞게 이용할 경우 더욱 발전된 최적의 시간을 얻을 수 있다. 지휘관이 전장 상황을 파악하여 이동시간을 예측할 수 있고, 유휴시간을 최대한 활용하여 융통성을 발휘한다면 일부 조정 가능하므로 좀 더 사격 종료 시각을 단축하여 작전 운용 면에서 최대한 능력을 발휘할 수 있기 때문이다(Kim, 2002).
2.2 계층분석방법에 관한 연구
계층분석방법(AHP)은 T.L.Satty(1970)에 의해 개발되었고, AHP는 다수가 의사결정을 해야 하는 문제에 대해 사용될 수 있는 의사결정 지원 방법론이라고 Harker(1989)는 설명하였다. 다수의 대안에 대하여 다수의 주제와 다면적인 평가 기준에 의한 의사결정을 위해 설계된 AHP는 의사결정자의 합리적이고 직관적인 판단을 근거로 주어진 문제를 계층화하여 정성적인 요소와 정량적인 요소를 동시에 고려하였다. 각 요소의 상대적 중요도를 쌍대비교하여 가중치를 측정하며 의사결정 문제를 해결하기 위한 포괄적인 틀을 제공하였다.
AHP는 전문가의 직관이나 오랜 경험 등을 바탕으로 평가하므로 수치로 표현이 가능한 정량적 평가뿐만이 아닌 정성적 평가 기준 또한 쉽게 처리할 수 있다. 각 계층요소의 우선순위와 중요도를 측정하기 위해 쌍대비교로부터 얻어지는 행렬의 특성치를 통해 우선순위와 상대적 중요도를 간편하게 구할 수 있고, 전문가들이 쌍대비교를 한 응답이 얼마나 타당한지에 대한 일관성비율(CR: Consistency Ratio)을 통해 그들이 성실하게 응답을 했는지 아닌지를 파악할 수 있다.
Choi(2015)는 AHP를 통해서 얻은 중요도가 유의미하려면 분석결과의 일관성이 먼저 확보되어야 한다고 하였다. 일관성에 대한 평가는 CR로 판단하는데, CR 값이 0.1 이하일 경우 일관성이 높고, 0.1~0.2 사이일 경우 자료로 사용하는 것이 용납될 수 있으며, 0.2 이상일 경우 일관성이 낮다고 판단하였다.
AHP 분석의 절차는 다음과 같은 4단계로 설정하였다. 1단계에서는 의사결정 문제를 상호 관련이 있는 사항들의 계층으로 분류한 후 설정한다. 2단계에서는 요소 간의 쌍대비교로 자료를 수집하고, 작성된 쌍대비교행렬은 행렬의 대각을 기준으로 역수의 값을 갖는다. 3단계에서는 고유치 방법을 활용하여 의사결정 요소들의 상대적인 가중치를 부여한다. 4단계에서는 여러 대안에 대한 순위를 얻기 위하여 요소들의 상대적 가중치를 종합화한다.
2.3 표준시간 선정에 관한 연구
Mundel과 Danner(1994)의 객관적 평가(OR)는 다양한 유형의 작업에 대하여 보통 속도의 기준을 설정하는 어려움을 극복하기 위해 개발되었다. 주관적 평가(Subjective Rating)는 사전에 분석자가 미리 작업의 난이도를 판단하여 타당한 표준 페이스를 마음속으로 그린 후 관측 페이스와 비교하여 수행도를 평가하는 것이지만, 객관적 평가는 작업마다 고유 특성을 반영하여 사전에 표준 페이스를 그린다는 것은 매우 어려우므로 하나의 기준작업과 비교하여 속도평가를 한 후 조정요인으로 난이도를 평가한다.
AHP를 통해 도출한 가중치와 직접 측정한 작업시간을 곱한 값을 작업시간에 더하여 조정된 작업시간을 생성하는 방법으로 속도평가를 수행한다. 그다음 난이도를 평가하는 조정요인으로 시험의 중량 기본 조정계수와 사용한 신체 부위에 따른 조정계수를 더한 값을 조정된 작업시간에 곱한 후 다시 더하여 정미시간(NT: Normal Time)을 구할 수 있다. 최종적으로 최적화된 시험순서를 설정하는 과정에서 하나의 시험과 그다음 순서 시험의 시험요인 변경 여부에 따라 추가 가중치가 부여된다. 추가된 가중치를 정미시간에 더한 값이 표준시간(ST: Standard Time)이 된다.
3. 폭발물 탐지시험 순서 결정
3.1 연구 과정
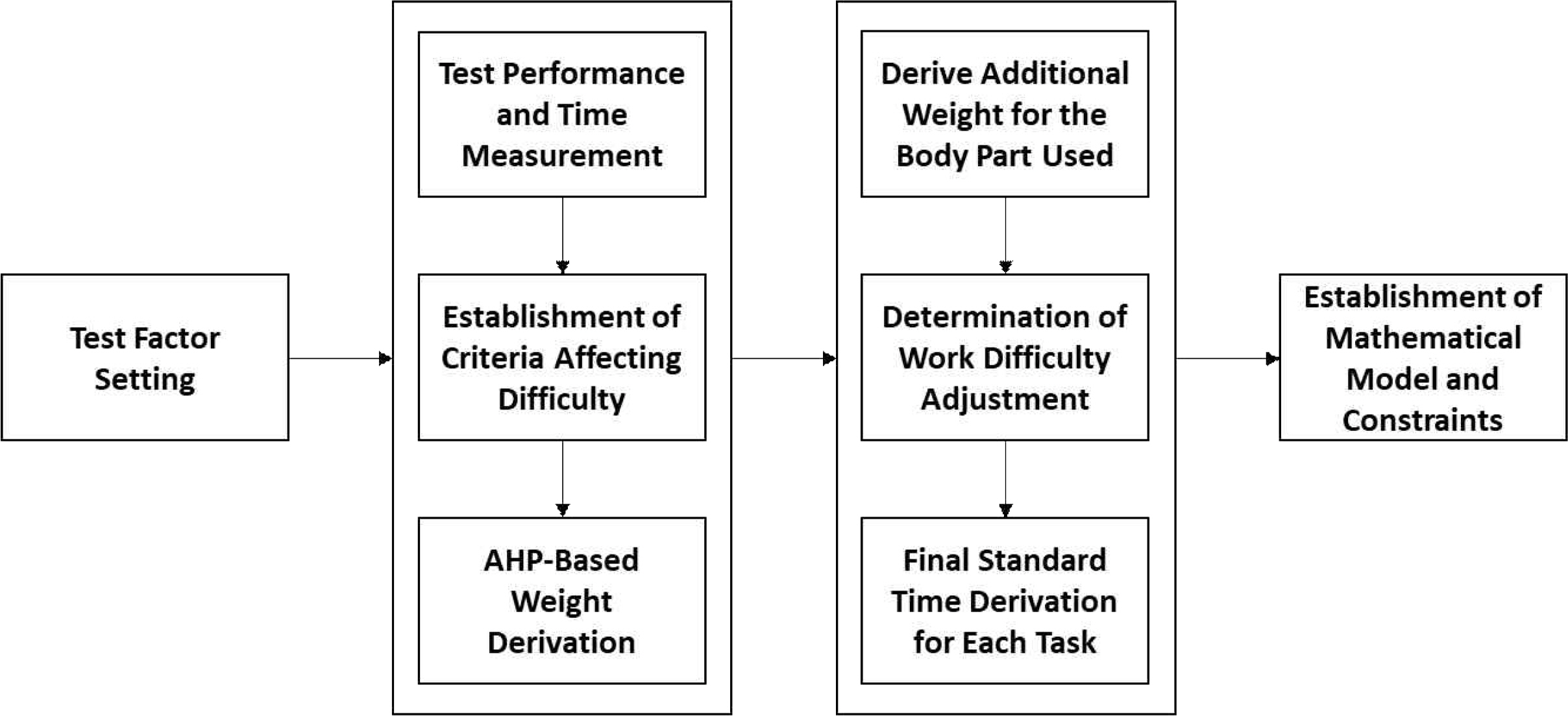
본 연구는 폭발물탐지장비의 최적화된 시험순서를 설계하면서 작업시간 단축 및 시험하는데 필요한 사람의 힘을 절감할 방법을 모색하였다. 이를 위해 관련 연구들을 통합하여 최적화된 시험순서를 도출할 수 있는 새로운 연구 과정을 수립하였다. 이 연구 과정을 그림으로 나타내면 아래의 Figure 1과 같으며, 시험요인 설정 후 연구에 필요한 가중치를 도출하기 위해 1, 2차 평가를 활용하여 수리적 모델을 수립하였다.
Research Process
본 논문의 연구 과정은 여러 가지 수행도평가 중, Mundel and Danner(1994)의 객관적 평가(OR)를 활용하여 작업의 수행도를 평가하는 것이다. 먼저 시험요인을 설정한 후, 각 시험의 작업시간과 시험을 직접 수행한 작업자가 판단한 난이도 척도인 AHP의 가중치를 활용하여 1차 평가를 진행한다. 1차 평가는 시험 직접 수행 및 작업시간 측정, 시험의 난이도에 따른 난이도 기준 설립, AHP에 기반한 가중치 도출로 구성되어 있다. 2차 평가는 시험의 중량 기본 조정계수와 사용 신체 부위에 따른 조정계수 도출, 작업난이도 조정계수 결정, 각 시험의 최종 표준시간 도출 순서로 진행된다. 마지막으로, 최적화된 시험순서를 결정하기 위한 수리적 모델과 제약조건을 설립한다. 최종 결과물인 최종 표준시간(ST)을 도출하는데 필요한 시간은 관측시간(OT: Observation Time), 정미시간(NT)이 있으며 식(1), (2)로 표현하였다. 식 (2)의 추가 가중치는 시험요인의 변경 여부에 따른 것이다.
3.1.1 시험요인 설정
시험요인은 총 15수준으로, 가방 종류 5수준, 폭발물 종류 5수준, 가방 방향 2수준, 폭발물 위치 3수준을 설정한다. 가방과 폭발물의 외형 및 무게, 가방의 지퍼를 여닫는 방법 등이 시험 중 작업자가 사용하는 힘의 크기를 크게 달라지게 하므로 가방과 폭발물의 종류는 최대한 모양과 재질이 다른 것으로 선택한다.
시험에 사용한 가방 종류는 총 5수준으로 캐리어, 백팩, 보스턴백, 핸드백, 크로스백이 있고, 각 가방의 무게 단위는 파운드(lb)로, Table 1에 표현하였다. 폭발물의 종류는 총 5수준이고, 모양과 크기, 재질, 무게가 상이하며 Table 2에 표현하였다. 무게의 단위는 가방과 같은 파운드(lb)이다. Table 3은 가방 방향 요인의 설명이다. Normal, Upside-down 2수준으로 나누어지고, 가방을 똑바로 놓았을 경우 Normal, 위아래 거꾸로 뒤집어 놓은 경우를 Upside-down이라고 정의한다. 폭발물 위치는 폭발물을 가방 안에 어떤 방법으로 숨기느냐에 따라 Normal, Hidden, Concealed 3수준으로 나누어진다. 폭발물의 위치가 Hidden과 Concealed일 때 Table 4와 같이 가방 안에 폭발물과 함께 들어가는 물건들의 종류가 상이하므로 추가되는 무게가 다르게 발생한다. 폭발물 위치 Hidden은 특정 종류가 아닌 여러 가지 물건들을 폭발물과 함께 가방 안에 숨기는 방법이다. 반면 폭발물 위치 Concealed는 폭발물탐지장비가 폭발물을 인식하지 못하게 하려고 전자기기인 노트북 사이에 폭발물을 끼워 넣고 가방 안에 숨기는 방법이다. 폭발물 위치에 따라 추가되는 물품들의 무게는 Hidden일 때 5.964 lb, Concealed일 때 3.781 lb이다.
Bag Type Factors
Explosive Type Factors
Bag Direction Factors
Explosive Location Factors
3.1.2 가중치를 도출하기 위한 난이도 기준
요인별 가중치를 도출하기 위해서 AHP를 활용하여 요인별로 쌍대비교를 한다. 이를 위해 요인들을 비교하는 기준 수립이 요구되며, 수립된 기준은 총 4개로 시험 도중 작업자의 힘이 많이 요구되는 요인에 더 큰 가중치를 부여할 수 있도록 설계하였다. 기준 1은 가방 내에 폭발물 삽입의 어려움으로, 가방 내에 폭발물을 넣을 때 전체적으로 힘이 많이 들거나 신경을 써야 하는 부분이 많은 요인에 가중치를 부여한다. 기준 2는 가방 내에 폭발물 삽입 시 폭발물의 손상 가능성으로, 폭발물의 재질이 무르거나, 가방이 단단하지 않아 폭발물의 손상 가능성이 큰 경우 가중치를 부여한다. 기준 3은 시험 준비 완료된 가방을 컨베이어 벨트로 이동 시 힘듦 정도로, 가방 방향 또는 종류에 따라 가방을 이동하기 힘든 경우 가중치를 부여한다. 기준 4는 가방 내에 폭발물 삽입 시 신체 사용의 불균등한 정도로, 손목 사용 정도나 손동작이 다른 요인에 비해 더 많이 필요한 경우 가중치를 부여한다.
3.2 AHP 모형 수립을 위한 1차 평가
3.2.1 시험 수행 및 시간 측정
AHP 모형 수립을 하기 위해 1차 평가인 수행도 평가를 진행한다. 수행도 평가를 이용하는 작업자는 다음 2개의 기준으로 판단한다. 첫째, 수행되는 작업에 대한 경험이 있어야 한다. 작업자는 사용되는 작업방법의 세부내용을 완전히 이해하기 위해 작업에 익숙해 있어야 한다. 실제 작업에 경험이 있는 사람을 작업자로 설정하는 것이 많은 도움이 되리라 판단되지만, 반드시 지켜야 하는 해당 사항은 아니다. 본 연구에서는 작업자 3명 모두 미리 작업방법에 대해 충분히 인지하였지만, 작업 경험이 있는 것은 아니었다.
둘째, 3회 이상의 독립된 연구의 평균 또는 3명 이상의 작업자 평균을 이용해야 한다. 이러한 표본은 동일 작업자로부터 시간을 달리하여 얻거나, 각기 다른 작업자로부터 얻을 수 있다. 중요한 점은 표본의 수가 증가함에 따라 오차가 줄어든다는 것이다. 본 연구에서는 3명의 작업자가 시험을 수행하였으며, 미리 설정한 시험순서대로 실제 시험을 진행하면서 각 시험의 관측시간과 총 무게를 측정한다. 사전에 설정한 시험순서는 50번의 시험 중 중복되는 것이 없고, 4가지의 요인들이 최대한 균일한 빈도로 설정될 수 있도록 하였다. 시험순서에 따른 시험요인 설정은 Table 6에 정리하였다.
The Setting of Test Conditions by Factors
3.2.2 AHP를 통한 가중치 도출
요인별 가중치를 도출하기 위해 실제로 시험을 수행한 후, 난이도에 영향을 끼치는 기준 4가지를 활용하여 가중치를 도출한다. AHP의 쌍대비교를 통해 가중치를 부여할 때 난이도 수치 즉, 점수가 갖는 의미는 Table 7과 같다.
The Meaning of Difficulty Level
먼저, 난이도 기준 4가지 중 어느 기준이 더 중요하다고 판단되는지 쌍대비교를 통해 기준의 가중치를 얻는다. Table 8을 참고하여 기준 1과 기준 2를 비교했을 때, 기준 1이 더 중요하다면 1행 2열에 정수의 수치를 입력하고, 2행 1열에는 1행 2열에 입력한 정수의 역수를 입력한다. 반대로 기준 2가 더 중요하다면 2행 1열에 정수의 수치를 입력하고, 1행 2열에 그의 역수를 입력한다. 쌍대비교행렬은 주 대각선에 있는 값이 모두 1이 되는 성질을 가지므로 1행 1열 및 2행 2열은 1의 값을 갖는다. 한 명의 작업자가 난이도 수치를 입력한 결과를 Table 8에 표현하였고, 각 값을 해당 열의 합으로 나누어서 표준행렬 Table 9를 만든다. Table 9의 같은 행의 평균값을 해당 행에 있는 기준의 가중치로 설정하여 가장 오른쪽 열에 입력한다.
A Pairwise Comparison Matrix for Obtaining Difficulty Level
A Standard Matrix for Obtaining Weights of Criteria
Saaty(1980)는 일관성 검정을 통해 행렬의 불일치성의 정도를 측정하며 이를 행렬의 크기에 따라 정규화하여 일관성지수(CI: Consistency Index)를 얻을 수 있다고 하였다. 일관성지수를 얻기 위해 먼저 쌍대비교행렬의 각 값과 해당 기준의 가중치를 행렬 곱셈하여 Table 10의 2열인 가중치 곱(Weighted Product)을 구한다. 다음으로, 가중치 곱의 값을 해당 기준의 가중치로 나누어 일관성측도(CM: Consistency Measure)를 구한다. 일관성지수는 Table 10의 4열에 있는 값 0.153으로, 구하는 식은 (CM 평균값- n)/(n - 1)이다. n은 행렬의 크기이며, 본 논문에서 n의 값은 4다.
Consistency Testing of Worker Responses
마지막으로, CI를 무작위지수(RI: Random Index)로 나누어 일관성비율(CR)을 도출한다. RI란 1에서 9까지의 정수들을 무작위로 추출한 후 역수 행렬을 작성하여 CI를 구한 것으로 Table 11에 표현하였다. CR 값이 0.1 이하일 경우 일관성이 높고, 0.1~0.2 사이일 경우 자료로 사용되는 것이 용납되는 수준으로 판단한다. 본 논문에서 사용한 모든 쌍대비교행렬의 CR 값은 0.2 이하로 용납할 수 있는 수준의 일관성을 가졌다고 판단하여 연구에 사용되었다.
Random Index
이처럼 일관성비율을 도출하는 과정을 3명 모두 진행한 후, 집단의사결정을 위한 의견취합 과정을 수행한다. 가중치를 산정하는 의사결정을 위한 집단의 의견취합 방법은 작업자 개별 가중치 도출 과정을 통해 얻은 개별적인 가중치를 취합하는 방식이다. 가중치 산정과 같은 개인의 의견을 취합하여 집단의 의견으로 도출하는 방식은 어떻게 취합하느냐에 따라 결과가 바뀔 수 있으므로 신중히 선택해야 한다. 본 연구에서는 개인별 쌍대비교행렬의 기하평균법(GMM: Geometric Mean Method)을 사용하여 집단의 쌍대비교행렬을 구성한 후 집단의 우선순위를 산정하는 방법인 AIJ(Aggregate Individual Judgments) 방식을 활용하였다.
AIJ 방식을 사용할 때, 기준 1과 기준 2에 대해 쌍대비교를 수행한 3명의 작업자의 응답 값이 각각 (1/4, 1/3, 1/4)이라면
Standard Matrix For Obtaining Weights of Criteria
요인별 가중치를 도출할 시 기준별 가중치를 도출하는 방법을 똑같이 적용하면 Table 13과 같이 총 15수준의 요인별 가중치를 얻을 수 있다. 15수준의 요인을 쌍대비교하므로 15C2인 105개의 값을 직접 얻어야 한다. 기준별 가중치를 도출할 때와의 차이점은 요인별 가중치를 얻는 과정의 마지막 단계에서 Table 13의 마지막 행에 삽입된 기준별 가중치와 각 요인의 기준별 가중치를 합산하여 최종적인 요인의 가중치를 얻어야 한다는 것이다. 최종 가중치는 해당하는 요인의 마지막 열에 작성하였다.
Final Weights of 15 Factors
3.3 작업난이도 조정계수 도출을 위한 2차 평가
3.3.1 수행도평가의 객관적 평가
여러 가지 수행도평가 중, Mundel과 Danner의 객관적 평가를 활용하여 작업난이도를 평가한다. 각 시험의 정미 시간을 계산하기 위해 작업난이도 조정계수(%)를 설정해야 한다. 작업난이도 조정계수는 중량 기본 조정계수(%)와 사용 신체에 따른 조정계수(%)로 이루어져 있다. 먼저, 중량의 조정계수를 도출하기 위해 각 시험의 1차 조정 작업시간을 1차 조정 작업시간의 합으로 나누어 작업시간 비율인 R(%)을 계산한다. 이를 통해 얻은 R 값이 5% 이하면서 중량이 20 lb 미만이면 중량의 조정계수로 기본 조정계수만 더한다. 반면, R 값이 5% 초과면서 중량이 20 lb 이상일 경우에는 기본 조정계수에 추가로 더해줄 수치가 존재한다. 본 논문에서는 모든 시험의 R 값이 5% 이하며 중량이 20 lb 미만이므로 기본 조정계수만 더한다. 중량은 소수점 첫째 자리에서 반올림하고, 해당 시험의 중량에 맞는 중량 기본 조정계수는 Table 15와 같다.
Basic weight adjustment factor
다음은 사용 신체에 따른 조정계수를 도출하는 방법이다. Table 16을 참고하여 해당 시험에서 사용하는 신체 부위를 먼저 찾는다. 사용 신체 부위 E(몸통 등), 눈과 손의 조화 K(집중할 필요는 없으나 눈을 떼지는 말아야 한다), 취급상의 주의 O(적당히 조심만 하면 된다)가 본 시험에 사용된 신체 부위 3가지이다. 3가지의 사용 신체에 따른 조정계수는 각각 8%, 4%, 1%이므로 총합은 13%이다. 모든 시험의 기본적인 동작이 같으므로 사용 신체에 따른 조정계수는 시험 1~50번까지 모두 13%로 같다. 50개 시험의 중량 기본 조정계수와 사용 신체에 따른 조정계수를 합한 것이 작업난이도 조정계수가 된다. Table 17의 2열에 작성한 각 시험의 무게를 소수점 첫째 자리에서 반올림하여 3열의 중량 기본 조정계수를 설정하고, 중량 기본 조정계수와 사용 신체에 따른 조정계수 13%를 더한 작업난이도 조정계수를 4열에 표현하였다. 각 시험의 (1+작업난이도 조정계수)를 조정된 작업시간에 곱하여 정미시간을 도출할 수 있다.
The Adjustment Factor by the Body Used
The Difficulty Adjustment Factor and Normal Time in Each Test
4. 실험분석 및 결과
4.1 시험요인 변경에 따른 추가 가중치
각 시험요인 가중치의 표준편차는 0.036(가방 종류), 0.015(폭발물 종류), 0.014(가방 방향), 0.034(폭발물 위치)이다. 가방 방향 요인을 제외한 나머지 3가지의 시험요인은 각각의 종류나 위치에 따라 편차가 크다. 따라서 시험을 진행하는 도중에 가방 종류나 폭발물 종류, 폭발물 위치를 변경할 때 추가적인 가중치가 부가되어야 한다. 다른 요인들에 비해 가방 방향을 변경하는 것은 추가적인 힘과 시간이 부가되지 않는다고 판단하여 제외하였다. 가중치는 사용 신체에 따른 조정계수를 활용하여 추가 부가한다. 가방 종류를 변경할 때, 새로운 가방을 바닥에서 들어 올려 시험대에 놓아야 하므로 사용 신체 부위 E2(다리의 힘으로 마루에서 들어 올린다)의 조정계수 10%를 정미 시간에 추가로 부여한다. 폭발물 종류를 변경할 때에는 사용 신체 부위 B(손목과 손가락)와 눈과 손의 조화 K에 따라 조정계수 5%를 추가로 부여한다. 마지막으로 폭발물 위치를 변경할 때, 사용 신체 부위 D(팔 등)와 눈과 손의 조화 J(어느 정도 쳐다보면 된다)에 따라 조정계수 7%를 추가로 부여한다.
4.2 연구 결과
1~50번까지의 시험번호 중, 첫 번째 순서로 수행하는 시험번호와 두 번째 순서로 수행하는 시험번호의 시험요인을 비교하여 가방 종류와 폭발물 종류, 폭발물 위치가 변경되는지 확인한다. 만약, 3가지 요인 모두 변경되었다면 변경 여부는 (1, 1, 1)로 표현되고, 변경 후 시험번호의 정미시간(NT)과 각 요인의 추가 가중치인 (0.1, 0.05, 0.07)과 (1, 1, 1)을 곱한 값을 정미시간에 합하여 두 번째 순서 시험의 표준시간(ST)을 도출한다. 본 시험의 제약조건은 시험순서 1~50에서 시험번호 1~50 중 모든 시험이 한 번씩 반드시 수행되어야 한다는 것이다. 시험의 목표 결괏값은 모든 시험을 수행하였을 때, 각 시험의 표준시간을 합한 총 표준시간이 최소화되는 값이다.
시험순서를 최적화하기 위해 표준시간을 최소화하는 수리식과 제약조건은 식(3)~식(6)으로 나타내었다. 수리식과 제약조건에 사용하는 변수는 Table 18에 정리하였다. a는 시험번호로 무작위로 나타날 수 있고, b는 시험순서로 1~50까지 순서대로 나타난다. 식(4)의 정미시간의 시험번호와 시험순서가 변경될 때 가방 종류, 폭발물 종류, 폭발물 위치의 변경 여부를 (i, j, k)로 나타낼 수 있다. 식(5)는 시험요인의 변경에 따른 추가 가중치를 나타낸 것이고, 식(6)은 최종적인 표준시간을 얻기 위해 추가 가중치와 정미시간을 곱한 후 정미시간을 더하는 식을 표현하였다.
Variables Used in Mathematical Formulas and Constraints
엑셀의 해 찾기 기능을 사용하여 목표 결괏값을 최소화한 결과, 총 표준시간은 2,798.87초(약 46.65분)가 도출되었다. 이는 1~50번의 시험을 차례대로 수행하였을 때 총 표준시간인 3,178.01초(약 52.97분)보다 379.14초(약 6.32분) 단축되었다.
5. 결론 및 추후 연구 과제
본 연구는 8종 항공보안장비 중 폭발물탐지장비의 성능을 향상하는 것을 목표로 장비의 검색능력이 원활한지 시험을 수행할 때, 작업자의 힘이 절감되고 작업시간이 단축되는 최적화된 시험순서를 도출한다. 이를 위해 1차 방법인 AHP를 활용하여 시험요인의 난이도에 따른 가중치를 부여하였고, 2차 방법인 객관적 평가를 활용하여 중량 기본 조정계수와 사용한 신체 부위에 따른 조정계수를 부여하였다.
이전 순서의 시험과 현재 시험의 시험 간 요인 변경 여부에 따른 추가 가중치를 최종적으로 부여하여 최종적인 표준시간을 도출할 수 있고, 모든 시험의 표준시간을 합한 총 표준시간이 최소화되도록 하는 시험순서를 선정할 수 있다. 최적화된 시험순서의 결과로 도출된 총 표준시간은 2,798.87초로, 초기의 시험순서대로 시험을 수행하였을 때에 비해 379.14초 단축되었다.
본 연구에서 AHP를 통해 가중치를 부여할 때 사용되는 AIJ 방식은 의사결정을 할 때 경험적인 자료나 선행연구가 부족하고 비전문가 집단에 의해 의사결정이 수행될 때 주로 이용된다. 이 방식을 활용하여 의사결정을 하는 경우 합리적인 근거를 제시하는 상당히 유용한 방법이지만, 더욱 다양한 요구사항과 집단지식이 효율적으로 반영되려면 기존 모델을 보완해야 할 필요가 있다(Hong et al., 2022).
본 연구는 실제 시스템을 대상으로 하는 연구이므로, 연구대상으로 이용된 폭발물탐지장비를 제외한 나머지 7종의 항공보안장비에도 활용할 수 있다. 작업자의 주관적인 의견에 따른 가중치 도출 방법과 시험 난이도 및 시험의 상황 변경에 따른 객관적인 가중치 도출 방법을 통합했다는 데에 시사점이 있다. 결과적으로, 작업자의 관점에서 가장 힘이 적게 드는 최적의 시험순서를 도출하였고 이를 총 표준시간의 최소화로 증명하였다. 이와 같은 방법을 활용하여 다른 항공보안장비의 성능시험을 하면 최적화된 시험순서를 얻을 수 있을 것이다.
Difficulty Criteria to Derive Weights
Additional Weight and Derived Standard Time Due to Test Factor Changes
