ESG투자를 통한 최적자산배분과 후생개선 요인분석에 관한 연구
A Study on the Analysis of Optimal Asset Allocation and Welfare Improvemant Factors through ESG Investment
Article information
Trans Abstract
Purpose
First, this paper suggests an alternative approach to find optimal portfolio (stocks, bonds and ESG stocks) under the maximizing utility of investors. Second, we include ESG stocks in our optimal portfolio, and compare improvement of welfares in the case with and without ESG stocks in portfolio.
Methods
Our main method of analysis follows Brennan et al(2002), designed under the continuous time framework. We assume that the dynamics of stock price follow the Geometric Brownian Motion (GBM) while the short rate have the Vasicek model. For the utility function of investors, we use the Power Utility Function, which commonly used in financial studies. The optimal portfolio and welfares are derived in the partial equilibrium. The parameters are estimated by using Kalman filter and ordinary least square method.
Results
During the overall analysis period, the portfolio including ESG, did not show clear welfare improvement. In 2017, it has slightly exceeded this benchmark 1, showing the possibility of improvement, but the ESG stocks we selected have not strongly shown statistically significant welfare improvement results. This paper showed that the factors affecting optimal asset allocation and welfare improvement were different each other. We also found that the proportion of optimal asset allocation was affected by factors such as asset return, volatility, and inverse correlation between stocks and bonds, similar to traditional financial theory.
Conclusion
The portfolio with ESG investment did not show significant results in welfare improvement is due to that 1) the KRX ESG Leaders 150 selected in our study is an index based on ESG integrated scores, which are designed to affect stability rather than profitability. And 2) Korea has a short history of ESG investment. During the limited analysis period, the performance of stock-related assets was inferior to bond assets at the time of the interest rate drop.
1. 서 론
연기금같은 장기투자자들은 자산운용에 있어 유사한 투자목표와 방법론을 갖고 있다. 그 중 첫째는 자산별 벤치마크(benchmark)대비 초과성과를 얻는 것이다. 이를 위해 가치평가(valuation)를 통한 주식선택(stock selection), 이례현상(anomalies)을 활용한 스타일투자, 스마트베타(smart β) 등의 투자를 행한다. 둘째로 장기투자자는 장기부채를 보유하므로 듀레이션 미스매칭을 줄일 수 있는 자산편입으로 재투자리스크(reinvestment)를 낮추고자 한다. 이를 위해 장기채권, 대체투자 등 장기성격을 갖는 자산, 자산간 상관관계가 낮은 우량자산 등을 발굴하고자한다. 셋째는 개별자산의 비체계적 위험(unsystematic risk)을 통제해 시장변동성 확대에도 포트폴리오 위험을 위험예산(risk budget) 내에서 감내할 수 있도록 안정적 자산군을 편입하여 포트폴리오 꼬리위험(tail-risk)을 제어하고자 한다.
최근 연기금의 자산운용은 시장효율성과 단기재무투자에서 벗어나 비재무적 요인(non-financial factors)인 환경, 사회, 지배구조(Environment, Social, Governance; 이하 ‘ESG’) 등을 적극 반영하는 통합운용을 확대하고 있다는 점이다. 국내 공적 금융기관투자가들의 책임투자규모는 2019년 기준 32.8조원으로 전체자산의 3.5%까지 확대되었지만 유럽 52.6%, 호주 50.6% 대비 낮은 수준으로 향후 국내 책임투자규모는 증가할 것으로 예상된다. 장기투자자는 수익성 뿐 아니라 공공성도 요구되고 있어 ESG투자를 통한 공공적 역할과 이론적 근거에도 관심이 확대되고 있다. 본 연구는 전략적 자산배분(strategic asset allocation)과 균형모형(equilibrium model) 방법론으로 ESG투자를 통한 최적배분과 후생개선 요인에 대한 분석을 통해 장기자산운용의 방향성을 제시하고자 한다.
2. 선행연구
ESG의 연구주제로는 ESG투자가 포트폴리오 초과성과와 기업가치 개선에 기여하는지에 대하여 가장 많은 연구가 이루어지고 있다. Dowell et al.(2000)은 환경규제를 엄격하게 적용하는 기업들의 Tobin’s Q가 높게 나온다고 하였고, Bauer et al.(2005)은 책임투자펀드가 일반펀드보다 우수한 성과를 낸다고 하였다. 반면 Di Giuli et al.(2014)은 기업들의 사회적 책임추구를 통한 이해관계자 이익증대가 기업가치 하락을 초래한다고 하였고, Mynhardt et al.(2017)은 거래유동성 부족으로 ESG인덱스가 전통지수 대비 열위하다고 보고하는 등 책임투자의 비효율성에 관한 연구를 발표하였다. 또한 Renneboog et al.(2008b)은 책임투자펀드가 일반펀드와 통계적으로 유의성이 없다고 하였다. 이처럼 책임투자에 대한 상반된 연구에도 불구하고 장기적으로는 ESG데이터 표준화, 다양성 등을 통하여 관련 연구는 지속적으로 확대될 것으로 보인다. 또 다른 ESG 연구방향으로 Hoepner(2013)는 포트폴리오에 ESG통합요인을 고려하면 포트폴리오 변동성과 꼬리위험이 개선됨을 보고하여 ESG투자의 위험대비 안정성 측면에 관한 연구를 보고하였고, Deng et al.(2013)은 인수기업의 사회적 책임이행지수가 높을수록 인수합병 공시기간에 인수기업과 피인수기업의 주가가 상승한다고 하며 인수합병(M&A)분야로 책임투자의 연구를 확대하였으며, Yoon et al.(2020)은 ESG에 관한 뉴스 등 미디어 공시의 시장영향력에 대한 연구를, 현상균(2021)은 ESG투자의 최적배분 요인분석을 발표하여 ESG와 재무분야의 연구분야를 확대하였다. 한편 이은지(2022)는 비정형 빅데이터분석을 통해 ESG연구 동향을 분석하였고, 이수열(2022)은 택배산업의 ESG인식과 서비스품질을 분석하였으며, 장지경(2021)은 공공기관의 사회적 책임과 재무적 성과의 연관성을 분석하는 등 ESG와 관련된 연구가 재무적 분석 이외에 다양한 분야로 연구가 확대되고 있다.
본 연구는 Xia(2001)의 장기채권시장과 투자자후생의 확실성등가부(Certainty Equivalent Wealth ; 이하 ‘CEW’) 개념을 확장하여 장기투자자가 ESG투자를 포함한 포트폴리오를 구성할 때 최적자산배분과 후생개선 지표로 활용할 수 있는 확실성등가부비율(CEWR)을 도출하였고, 이에 관한 요인분석과 해석을 하였다.
3. 모형의 가정과 정의
3.1 모형설계의 가정 및 정의
1) 경제의 불확실성(uncertainty)은 확률측도공간(Probability Measure Space)인 (
2) 개별불확실성인 zS, zr, zE 등은 브라우니안 모션(Brownian Motion)으로 표현된다고 가정하였고, 이는 확률측도 P에서 정의하였다.
본 연구는 ESG자산 편입을 통한 포트폴리오의 운용에 초점을 두고 있어 전통자산인 주식과 채권을 고려한 자산배분을 하였다. 이를 통해 ESG투자가 포함된 최적 자산배분비중과 포트폴리오 후생개선에 영향을 주는 요인분석을 하고자 한다. 우선 주식, 채권, ESG 등 3개 자산을 기준포트폴리오를 구성하였고, ESG 추가에 따른 포트폴리오 후생개선을 확인하기 위해 ESG의 비교자산으로 KOSDAQ을 선정하였다.
3.2 자산확률과정과 동역학 (Dynamics)
1) 주식은 기하 브라우니안 모션(Geometric Brownian Motion ; 이하 ‘GBM’) 확률과정을 가정한다.
(σS는 주가수익률 변동성, λS는 주식에 대한 위험프리미엄, dzS는 주식의 불확실성)
2) 채권이자율은 Vasicek모형을 가정하였다.
(σr은 채권이자율에 대한 변동성, κ는 단기이자율이 평균으로의 회귀속도,
3) ESG도 GBM확률과정을 가정하였다.
(σE는 ESG변동성, λE는 ESG에 대한 위험프리미엄, dzE는 ESG의 불확실성)
4) Pricing Kernel인 확률적 할인요인(Stochastic Discount Factor)은 다음의 확률과정을 가정하였다.
∅ = (∅S, ∅r, ∅E'는 주가수익률, 채권이자율, ESG수익률에 대한 시장위험가격(Market Price of Risk ; 이하 ‘MPR’) 벡터이며, MPR은 물리적 측도와 EMM(Equivalent Martingale Measure)을 연결하는 매개체이다.
E[dzSdzr]=ρsrdt,
E[dzEdzr]=ρErdt,
E[dzSdzE]=ρSEdt으로 가정한다.
주가, ESG는 동일한 GBM확률과정을 가정하므로, 상기 가정의 Pricing Kernel을 이용하면 다음의 동역학(dynamics)을 유도할 수 있다.
Pricing Kernel을 이용한 주가의 확률과정은
여기서 λS≡-(∅S+∅rρSr)
채권단기이자율은 Vasicek과정을 가정한다. 할인채권가격은 지수아파인(exponential affine)형태를 따르고, 모든 상태변수는 가우시안(Gaussian) 형태를 가지므로 채권가격은 Pricing Kernel 적률형태를 통해 계산할 수 있다.1)
함수 A(•), B(•)는 FPDE(Fundamental Partial Differential Equation)를 만족하며 B(t, T)는 다음과 같다.
채권가격에 이토램마(Ito‘s Lemma)를 적용하면 다음의 SDE(Stochastic Differrntial Equation)를 만족한다.
λr ≡ -(∅r+∅SρSr) 이다.
ESG도 동일한 확률과정으로 유도하였다.
여기서 λE ≡ -(∅E+∅rρEr)
3.3 자산별 최적배분비중 도출
상기에서 가정한 자산의 정의와 확률과정모형을 통해 ESG를 편입한 포트폴리오의 최적투자배분을 구할 수 있다. 투자자의 효용함수는 Brennan et al.(2002)과 같은 등탄력성효용함수(Isoelastic Utility Function)를 사용하였다. 상태변수(state variable)의 채권이자율만을 고려하여 최적화(optimization)문제를 해결하기 위해 Bellman 방정식을 이용한 제일계조건(First Order Condition)도출을 통해 자산의 최적배분비중을 각각 도출하였다.2)
제약조건
Maxx는 자산배분벡터인
간접효용함수를 편미분하여 최적화하면 다음의 최적투자배분이 결정된다.
여기서
3.4 CEW적용을 통한 후생의 도출
‘간접효용함수의 분리성’을 이용하면 ESG자산이 존재하는데도 투자를 하지 않았을 경우의 간접효용함수가 아래와 같이 분리된다.
J(W, r,t)NE는 ESG를 투자하지 않았을 경우의 간접효용함수이고, J(W, r,t)는 모든 자산에 투자할 때 간접효용함수이다.
함수 g(t)는 행렬지수함수형태를 가정하였다.
정리하면 dNE(t, T) = d(t, T) + f(t, T)의 관계가 성립하며, d(t, T) 는 최적포트폴리오에 투자하는 경우 식(13)의 우측 로딩함수를 의미하고, dNE(t,T)는 ESG투자가 가능함에도 투자하지 않는 경우에 계산되는 식(13) 좌측식 d(t, T)를 의미한다. 이를 통해 아래의 미분방정식이 성립한다.
만일 f(•)이 항상 (-)의 값을 가지는 경우 g(•)가 1보다 작게 되며, J(W, r,t)NE ≺ J(W, r,t)이 성립하게 되어 ESG투자가 가능함에도 이를 투자하지 않는다면 전체 투자의 후생이 낮아지는 것으로 해석할 수 있다. 후생의 차이를 정교하게 계산하기 위해 CEW를 추가로 정의하면 시점 t에 자산투자를 위해 1원을 투자하고, 만기시점 (T, t < T)까지 자산을 운용한다고 할 때 이 경우 t시점에서 평가하는 만기시점까지 기대효용은 아래와 같다.3)
CEW는 이와 동일효용을 주는 만기시점 확실성 부의 양(sure amount of wealth)을 의미하고, 만기CEW의 효용은
CEW = exp [(c(t,T)r + d(t,T)]
효용이론에서 정의하는 CEW는 시점개념과는 무관하지만, 본 연구는 만기시점의 효용을 비교하는 방식을 적용하였다. 상기 CEW식을 이용하면 추가적 자산추가를 통한 후생개선비율인 CEWR*을 구할 수 있게 된다.
①CEW* = exp[(c(t, T)r+d(t, T)*]
②CEW1= exp[(c(t, T)r+d(t, T)1]
③
CEWR*은 아래와 같이 나타낼 수 있다.
ESG를 편입한 3개 자산 포트폴리오의 후생개선을 파악하는 것이 본 연구의 핵심으로 연구의 엄격한 조건을 위해 비교대상자산4)을 선정하였다.
ESG가 편입된 포트폴리오의 후생개선여부를 확인할 수 있는 CEWR은 계산상 편의를 위해 ESG가 포함된 3개 자산 비율인 CEWRE와 비교자산인 KOSDAQ을 포함한 CEWRQ를 아래와 같이 정의하여 산출하였다.
①
②
③
CEWR이 기준 1을 상회하면 ESG의 후생인 CEWRE가 비교대상자산의 후생인 CEWRQ대비로 개선되었음을 의미하고, 기준 1을 하회한다면 후생개선이 이루어지지 않았음을 나타낸다.
4. 모형의 실증분석
4.1 자료 및 추정방법
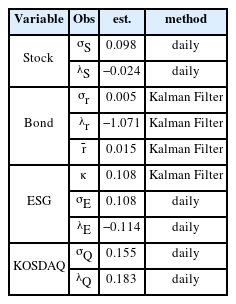
모형추정을 위한 자료는 2014년 1월~2019년 12월까지 일별자료를 사용하였다. 주식은 KOSPI(배당반영), 채권은 만기가 각각 1년, 2년, 3년, 5년, 10년 만기 일별수익률을 사용하였다. 또한 ESG주식은 KRX ESG Leaders 150 (배당반영), 비교대상자산으로는 KOSDAQ의 일별수익률을 사용하였다. 또한 채권모형추정의 주요 파라미터는 칼만필터(Kalman Filter)를 사용하여 추정하였다.5) 상대적 위험회피도 γ는 장기투자자의 위험회피수준이 보수적이라는 점을 감안하여 Xia(2001) 등의 연구와 같이 위험회피의 중간수준인 5를 기준값으로 적용하였다.
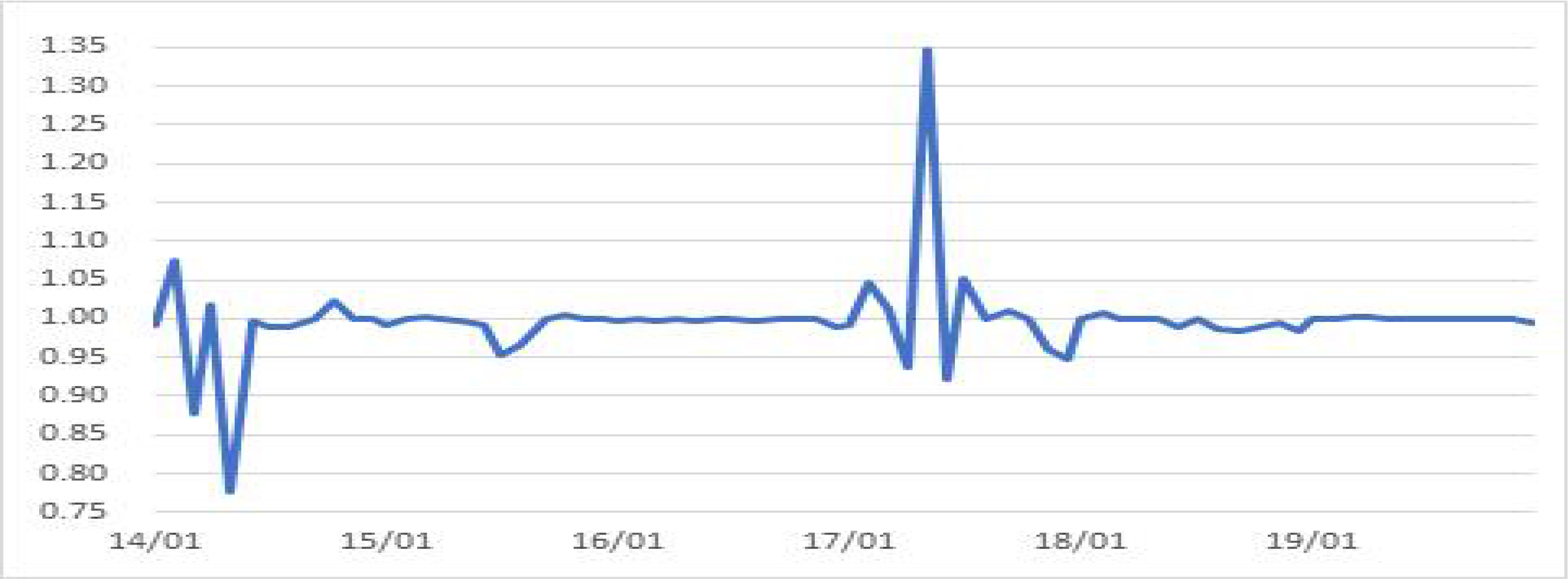
[Figure 1]에서 CEWR 시계열추이를 보면 대부분 기간 기준 1수준에 위치하고 있다. 이는 ESG 편입이 분석기간 동안 유의미한 후생개선을 이루지 못했다고 해석할 수 있다. 이는 해당 기간동안 비교대상자산 KOSDAQ이 ESG보다 우월한 성과를 나타냈기 때문이기도 하고, 한국형 스튜어드십코드를 도입한 2016년 직후 일시적으로 관심이 높아지며 기준 1을 상회하기도 하였으나 이후 ESG에 대한 관심이 낮아졌기 때문이기도 하다. CEWR이 통계적으로 유의미하지는 않았지만 분석기간 후반으로 갈수록 소폭 기준 1을 상회한다는 점에서 ESG투자가 포트폴리오 후생개선에 영향이 없다고 단정할 수는 없다. 따라서 이번 연구의 방법론을 활용하여 유럽 및 미국 등 ESG도입 역사가 오래된 국가들의 후생개선 여부도 확인하여 볼 유인이 있다.
4.2 자산별 최적투자배분 요인분석
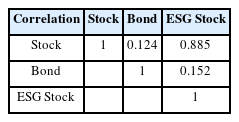
본 절에서는 최적자산배분의 비율이 어느 변수에 영향을 받는지 회귀분석을 통해 직관적 분석을 해보고자 한다. 즉, 종속변수를 포트폴리오의 자산별 최적 투자배분으로 하고, 추정모수를 설명변수로 한 회귀분석을 하였다. 설명변수로는 주식수익률(μS), 채권이자율(r), ESG수익률(μE), 주식변동성(σS), 채권이자율변동성(σr), ESG변동성(σE), ESG와 채권이자율 상관계수(ρEr), 주식과 채권이자율 상관계수(ρSr), 주식과 ESG 상관계수(ρSE), ESG와 채권이자율 상관계수(ρEr) 등이다.6)
1) y1 = constant + β1r + β2μE + β3σr + β4σE + β5ρEr + ε
2) y2 = constant + β1μS + β2μE + β3σS + β4σE + β5ρSr + β6ρEr + β7ρSE + ε
3) y3 = constant + β1μS + β2r + β3σS + β4σr + β5ρSr + ε
이를 통해 수식(8)의 최적배분 자산벡터
4.3 CEWR요인분석
본 절은 핵심변수인 CEWR에 어떤 변수가 영향을 미치는지 회귀분석을 하고자 한다. 즉 CEWR을 종속변수로 하고, 추정 파라미터와 최적배분비중을 설명변수로 다중회귀분석을 하였다. 설명변수는 주식수익률(μS), 이자율(r), ESG수익률(μE), KOSDAQ수익률(μQ), 주식변동성(σS), ESG변동성(σE), KOSDAQ변동성(σQ), 주식·이자율 상관계수(ρSr), ESG·이자율 상관계수(ρEr), 주식· ESG 상관계수(ρSE), 주식·KOSDAQ 상관계수(ρSQ), KOSDAQ·이자율 상관계수(ρQr), 최적주식비중(x*S), 최적채권비중(x*r), 최적ESG비중(x*E)을 기본설명변수로 주식·이자율 최적비중, 채권·ESG 최적비중, 주식·ESG 최적비중을 각각 추가한 y4, y5, y6를 분석하였다.
4) y4 = constant + β1μS + β2σS + β3μE + β4σE + β5μQ + β6σQ + β7ρSr + β8ρSE + β9ρEr + β10ρSQ + β11ρQr + β12r + β13x*S + β14x*r + ε
5) y5 = constant + β1μS + β2σS + β3μE + β4σE + β5μQ + β6σQ + β7ρSr + β8ρSE + β9ρEr + β10ρSQ + β11ρQr + β12r + β13x*r + β14x*E + ε
6) y6 = constant + β1μS + β2σS + β3μE + β4σE + β5μQ + β6σQ + β7ρSr + β8ρSE + β9ρEr + β10ρSQ + β11ρQr + β12r + β13x*S + β14x*E + ε
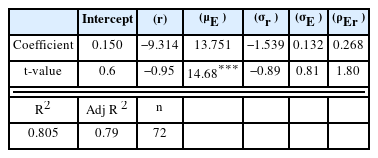
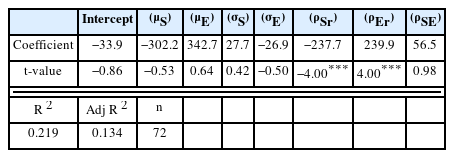
식(12)를 통해 추정한 CEWR을 종속변수로 한 결과를 보면 첫째로 채권수익률을 설명변수로 한 분석에서 이자율은 CEWR에 음(-)의 영향을 주었는데 이는 금리가 상승할 때에 CEWR이 상승함을 의미한다. 즉 금리 상승기에 ESG자산을 포함한 자산배분의 후생이 개선된다는 것으로 금리상승기에 일반적으로 경기가 개선되지만, 자금조달비용도 상승하면서 한계기업 부실화에 따른 금융시장 리스크가 증가함을 감안하면 안정적 자산으로서 ESG자산의 포트폴리오 편입 필요성이 높아진다고 설명할 수 있다. 둘째로 최적 주식비중과 최적 ESG비중도 CEWR에 음(-)의 영향을 주었는데 분석한 기간 동안은 전반적인 저금리기간으로 우리나라 주식관련 자산들이 채권 대비로 낮은 위험조정수익률을 나타내 주식 및 ESG자산이 포트폴리오의 효용을 개선하는데 낮은 기여를 하였기 때문으로 볼 수 있다. 셋째로 채권의 최적 비중이 CEWR에 양(+)의 영향을 주었는데 이 또한 2008년 금융위기 이후 전반적인 금리하락기가 지속됨에 따라 채권이 다른 자산 대비 우월한 자산이었던 점에 영향을 받은 것으로 보인다.
이번 연구에서 CEWR은 최적 자산배분비중 요인분석과 달리 각 자산수익률과 변동성이 큰 영향을 주지는 못하는 것으로 분석되었다. 이는 첫째로 종속변수에 영향을 주는 파라미터들이 비선형모형을 선형화하는 과정에서 주요 변수 간의 유의성을 낮추는 효과가 있었던 것으로 보이고, 둘째로는 재무적 성과를 추구하는 최적 자산배분비중은 수익률과 변동성 등에서 많은 영향을 받지만 재무적요인과 비재무적요인을 통해 장기적 효용을 반영하는 ESG투자는 단기수익성과 변동성보다는 장기적으로 포트폴리오의 자산배분에 더 큰 영향을 줄 수 있다고 해석할 수 있다. 따라서 이번 연구의 결론을 단정하기보다는 다양한 국가와 벤치마크들의 분석을 통하여 CEWR에 대한 추가적인 해석을 할 필요가 있고, 장기투자자의 입장에서는 차별성있는 자산들의 지속적인 편입을 통해 포트폴리오의 자산배분 안정성을 높여야 포트폴리오의 후생을 개선시킬 수 있다는 장기투자자의 자산배분의 대원칙은 유효하다고 볼 수 있다.
5. 결 론
본 연구의 차별성은 첫째, 연기금 ESG투자의 비중 확대를 감안하여 이를 균형모형을 통한 자산배분에 적용하였고, 이를 후생으로 환산하는 정량적 방법론을 제시하여 최적자산배분과 포트폴리오 후생개선 여부를 동시에 분석하였다는 점에 있다. 둘째, ESG투자가 장기투자자의 재무수익과 후생개선에 기여할 수 있는가를 각각의 설명변수에 대하여 분석의 의미를 확장하였다는 점에서 그 의의가 있다고 하겠다. 그리고 셋째, 균형이론을 이용하여 ESG의 포트폴리오 편입에 따른 후생개선을 확인하기 위해 비교자산으로 KOSDAQ지수를 포함한 3개 자산 포트폴리오의 CEWR식을 도출하였는데 이를 통해 자산별 최적 투자비중과 CEWR에 영향을 미치는 요인을 분석하여 장기투자자의 투자목적에 맞는 자산배분을 선택할 수 있도록 아이디어를 제공하였다.
결과적으로 분석기간 동안 연구의 주요 관심대상인 ESG를 포함한 포트폴리오가 후생개선의 뚜렷한 결과를 찾지는 못하였다. 즉, 2017년 이후 CEWR이 기준점인 1을 소폭 상회하며, 개선가능성을 보여주었지만 아직은 우리가 선정한 ESG자산이 주식자산과 차별성이 있는 자산으로 통계적으로 유의미한 후생개선 결과를 나타내지는 못하였다. 하지만 분석을 통해 최적자산배분과 사회적 후생개선에 미치는 요인이 서로 다르다는 점을 확인할 수 있었고, 최적자산의 배분비중은 자산수익률, 변동성, 주식·채권의 역상관관계 등 요인의 영향을 받는 것으로 나타나 전통적 재무이론과 유사한 결과를 보였다.
CEWR을 종속변수로 하는 회귀분석을 통하여 CEWR은 금리상승기와 최적 주식비중 및 최적 ESG비중이 낮아질 때 후생개선에 유의미함을 보인다는 점에서 포트폴리오 후생은 자산배분 효과에 의해 더 큰 영향을 받는다고 해석할 수 있다. 즉 최적 자산비중은 단기수익성 영향을 많이 받고, 포트폴리오 후생은 전략적 자산배분에 영향을 많이 받는다는 것을 확인할 수 있어 투자자의 철학과 투자기간을 감안하여 최적 자산배분비중을 중간목표로 설정할 것인지, 후생관점에서 포트폴리오의 운용을 결정할 것인지에 대한 의미를 부여할 수 있었다.
ESG투자가 후생개선에 유의미한 결과를 나타내지 못한 원인으로는 본 연구에서 선정한 KRX ESG Leaders 150 이 ESG통합점수에 기반한 지수로, 수익성보다 안정성에 영향을 주도록 설계된 지수의 성격도 영향을 미친 것으로 보인다. ESG등급을 이용한 지수가 직관적으로 환경, 사회 및 지배구조를 모두 통할하는 좋은 지수산정방식이지만 수익성 측면에서는 많은 문헌연구에서 유의미한 성과를 내지 못했다는 한계점도 갖고 있다. 또한 우리나라는 ESG투자 역사가 길지 않고, 벤치마크가 부재하다는 점도 한 원인이 될 수 있다. 마지막으로 분석기간 동안 비교지수인 KOSDAQ대비로 상대적 성과가 열위하였고, 금리하락 시기에 주식관련 자산이 채권자산대비로 성과가 열위하다는 점도 유의미한 결과를 도출하는데 한계로 작용하였다고 볼 수 있다.
Notes
채권가격산출은 장기투자자의 ESG투자를 통한 후생개선과 포트폴리오선택(2022) 현상균 박사학위논문 p33-35참조
최적화과정은 장기투자자의 ESG투자를 통한 후생개선과 포트폴리오선택(2022) 현상균 박사학위논문 p36-38참조
간접효용함수는 장기투자자의 ESG투자를 통한 후생개선과 포트폴리오선택(2022) 현상균 박사학위논문 p39-42참조
자산추가효과에 기인한 후생개선을 배제하기 위해서 주식자산의 대표지수로 선정한 KOSPI와 종목구성이 중복되지 않고, ESG자산 대비로 KOSPI와의 상관계수도 낮으며, 기간수익률도 우수한 KOSDAQ을 비교대상지수로 선정하였다.
채권모수추정은 장기투자자의 ESG투자를 통한 후생개선과 포트폴리오선택(2022) 현상균 박사학위논문 p48-49참조
현상균, 이정석, 이준희(2021)는 Q측도의 주요변수인 market price of risk를 변수로 사용했으나 설명력이 낮아 본 연구에서는 추가로 타 변수를 사용하였다.