2.1 손익분기점 분석

한국은행에서 매년 발간하는 기업경영분석에서는 손익분기점률에 대해 다음과 같이 설명하고 있다.

“손익분기점률은 매출액에 대한 손익분기점에서의 매출액의 비율로서 일반적으로 이 비율이 낮을수록 영업활동의 채산성이 양호하고 높을수록 채산성이 좋지 않음을 의미한다. 손익분기점에서의 매출액은 일정기간의 수익과 비용이 같아서 이익이나 손실이 발생하지 않는 경우의 매출액을 말한다. 매출액에서 변동비를 공제한 차액인 한계이익을 매출액으로 나눈 비율을 한계이익률이라 하는데 고정비에서 영업외수익을 차감한 금액을 이 한계이익률로 나누면 손익분기점에서의 매출액이 된다.”

1)고정비=판매관리비+영업외비용+(노무비의1/2+제조경비-외주가공비+재고조정중의고정비))

2)변동비=총비용-고정비

3)재고조정중의고정비=(매출원가-당기총제조비용)×노무비의12+제조경비-외주가공비당기총제조비용

4)총비용=매출원가+판매관리비+영업외비용

이 설명에 따르면 변동비는 대체로 재료비와 노무비의 12 그리고 외주가공비로 한정되고 있다. 이는 비용 항목의 특성 상 명확히 변동비의 행태를 가지는 재료비 및 외주가공비와 함께, 부분적으로 변동비 특성을 보이는 노무비의 경우 임의적으로 반 정도만을 변동비에 포함하고 있음을 알 수 있다. 이렇게 변동비를 결정하는 방식이 논리적으로 타당한가에 대한 지적은 있을 수 있으나, 현실적으로 변동비를 정밀하게 측정할 수 없다면 이러한 경험칙(經驗則)에 따른 변동비 분류에 의한 산업의 BEP 분석은 개별 기업의 각각 다른 변동비 행태를 포괄할 수 있다는 점에서 실무적 타당성을 가지는 것으로 판단된다.

공식에 따르면 결국 손익분기점은 변동비와 고정비의 관련비(ratio)에 따라 달라짐을 알 수 있으므로, 기업 또는 산업의 비용구조(cost structure)를 보여 주는 매우 중요한 재무보고서 상 숨겨진 정보(hidden information)의 하나로 볼 수 있다.

이하 수리적 분석의 편의를 위해 재무보고서 항목을 수학적 기표로 전환한다. 손익계산서로부터 순이익(π(x))은 매출(x)에서 매출원가(M), 판매관리비(G), 순영업외비용(I-R), 그리고 법인세(T)를 차감한 금액이다. 이를 수식으로 표현하면 다음과 같다.

이하 분석은 법인세를 제외하고 이익을 세전이익으로 간주한다. 위 식 매출원가(M)를 변동매출원가 v(x)와 고정 매출원가(F_m)로 양분한 후, 백분율 손익계산서 수치를 적용하면 즉 모든 파라미터를 x로 나누면, 이익률(π)은 다음과 같이 표시할 수 있다.

단, v=v(x)x

이익률이 0인 손익분기점률 x₀은 다음과 같다.

이제 상기식의 분자는 모두 고정비 항목으로 묶어서 f로 표기하도록 한다.

2.2 변곡점과 변곡접선

전통적인 CVP 분석 관점에서 실제의 개별 비용은 조업도(매출)에 따른 변동의 행태(cost behavior)가 다양하게 나타나지만, 총비용은 개별 비용들의 합산으로 포괄적으로 준변동비(semi variable cost) 즉 다음 1차 선형함수 f(x)의 행태를 보일 것이라는 기본 전제에 따른다.

단, v는 매출액 대비 변동 비율

이러한 선형성 가정을 전제로 한 BEP 및 CVP 분석은 경영학, 특히 관리회계, 재무관리 영역뿐만 아니라 생산관리, 품질관리 등에서도 매우 유용한 도구로 받아들여지고 있다. 선형의 비용함수가 단기적·국지적·미시적 관점의 어떤 관련 범위(relevant range) 내에서 타당성을 가진다고 볼 수 있으나, 그 범위를 벗어난 장기적·광역적·거시적 관점에서는 비선형(nonlinear) CVP 분석이 요구된다. 최근 관련 연구(Danijela Martinovic, 2019)에서도 현재 역동적인 경영환경 하에서 비선형 손익분기점 모형의 필요성 또는 중요성에 대하여 언급하고 있다. 그러나 대부분의 선행 연구는 다음 Figure 1에서처럼 비선형의 개념적 소개에 그칠 뿐 구체적인 비선형 관계식의 도출 과정이나 모형 개발에 대한 기술(description)이 없다.

Figure 1.

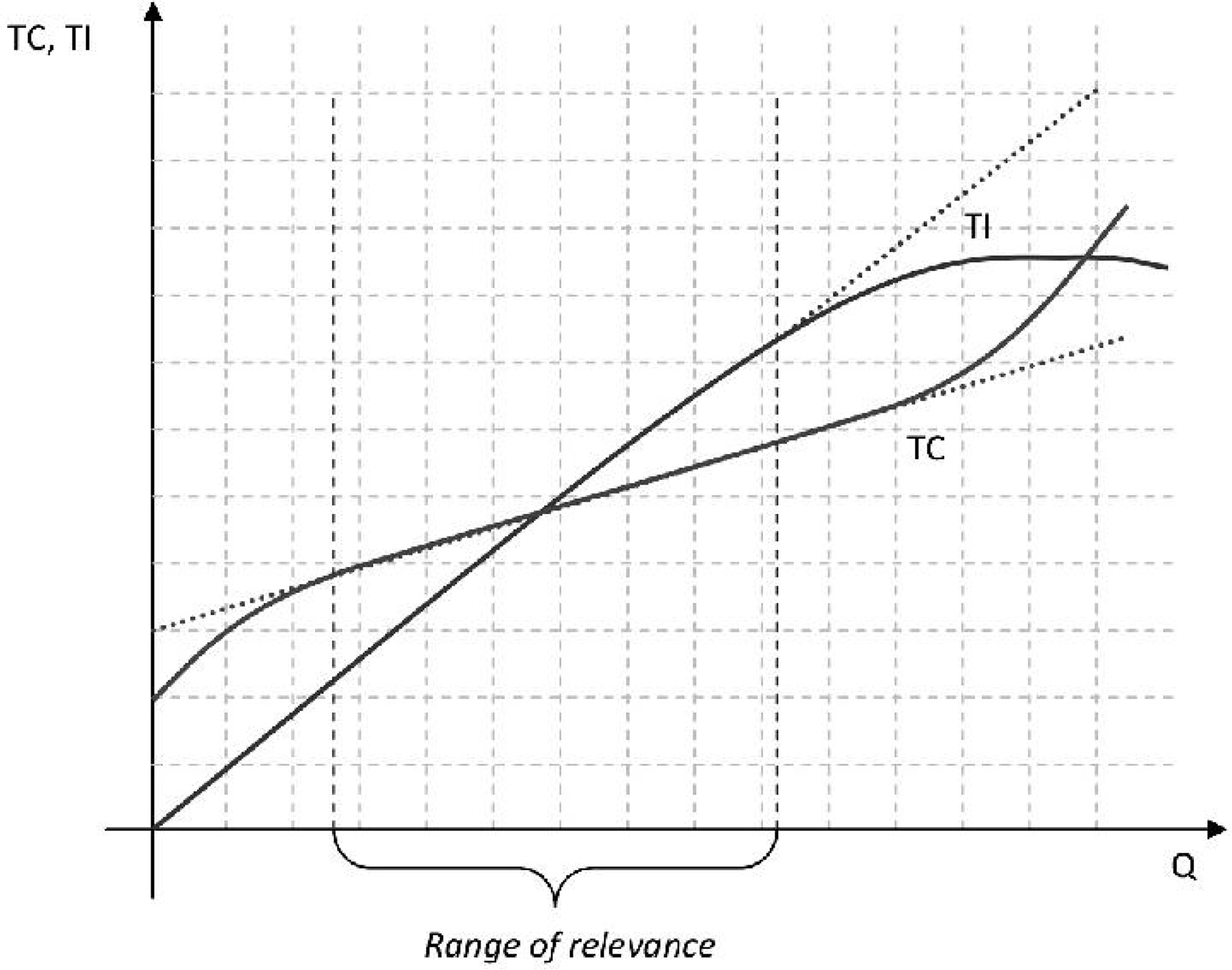
The break-even point with the nonlinear course of the development of the total income and costs

Original Source: Dvorski i Luža, 2007, 189 Source: Danijela Martinovic(2019), p.230

그렇지만 Figure 1에서 볼 수 있는 바와 같이 선형 비용함수가 미시경제학에서 말하는 3차 비용함수(cubic cost function)의 변곡접선과 일치한다는 사실은 매우 중요한 함의를 가지고 있다. 손익분기점을 지나는 1차 비용함수는 3차 비용함수의 변곡점(inflection point)을 지나는 접선, 즉 변곡접선(infection tangent)이어야 하며 이는 하나 뿐인 변곡점의 유일한 접선이라는 사실을 상기할 필요가 있다. 다시 말해 1차 비용함수의 손익분기점이 3차 비용함수의 변곡점과 같음을 인지하는 것이 본 연구의 분석적 전개 과정의 핵심이라고 할 수 있다.

3.1 표준형 3차 함수

미시경제학 문헌에서는 대부분 3차 비용함수에 관해서 사례에 의한 예시(illustration)에 그치고(Paul, 2017; Scott et al., 2021), 비용함수의 각 계수는 가상의 수치를 대입하여 비용곡선을 설명하고 있다(Erfle, 2014). 다음 그림이 그 대표적인 예이다.

Figure 2.

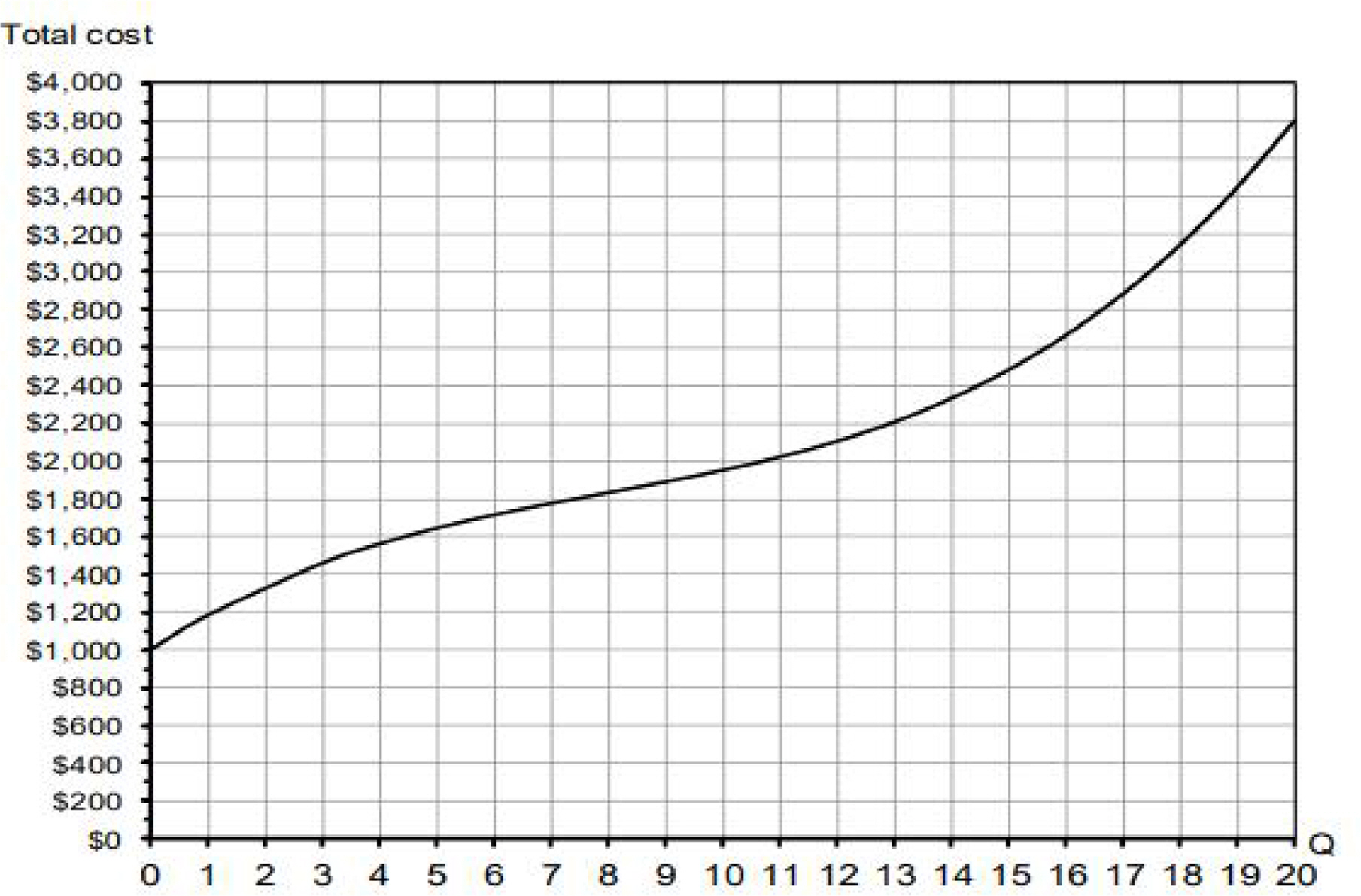
A Cubic Total Cost Curve

Source: Erfle, Stephen, 2014, p.4 Deriving a cubic total cost function from a cubic total cost curve

따라서 대부분 3차 비용함수에 대해 다음과 같이 일반형 3차 함수로 논의를 전개하고 있다.

본 연구는 구체적인 비선형 CVP 분석을 위한 총비용곡선으로 상기 3차 비용함수의 일반형을 다음과 같이 2차항이 제거된「완전 세제곱식+일차식」의 꼴 즉 표준형 3차함수로 나타낼 수 있다는 사실에서 출발한다.

3차 비용함수를 1차 미분하면 g'(x)=3ax2+2bx+c, 2차 미분하여g"(x)=6ax+2b=0 으로 두면, x=−b3a로서 변곡점의 x좌표를 알게 되고, 이를 g^'(x)에 대입하면 변곡점 p에서 접선의 기울기 c-b23a를 얻을 수 있으며, 또한 g(x)에 대입하면 변곡점의 y좌표 g(x0)=d-bc3a+2b327a2를 얻을 수 있다. 따라서 일반형 3차 비용함수의 변곡점에서 접선의 방정식은 1차식으로 g'(x)=(c-b23a)(x+b3a)+d-bc3a+2b327a2이므로 g'(x)=(c-b23a)x+d-2b327a2 이다. 이를 mx+n으로 간결하게 나타내고, g(x)를 표준형으로 표시하면 다음과 같다.

상기 표준형 3차 비용함수에서 완전제곱꼴 a(x - p)³을 제외한 1차식 mx + n이 바로 변곡점을 지나는 변곡접선의 방정식이며, 이는 전통적 CVP분석에서 가정하고 있는 1차 비용함수 f(x) = vx + f와 완벽하게 대응하는 직선으로써, 당연히 1차 비용함수에 의한 손익분기점은 3차 비용함수의 변곡점에 해당한다.

수학적 정의에 따르면 함수 f(x)가 두 번 미분 가능한 함수일 때 점 p에서 g′′(p) = 0이고 x = p 근방에서 g′′(p) 의 부호가 바뀌면, 점 (p, g(p))는 y = g(x)의 변곡점이 된다. 따라서 일반형 비용함수의 2계 도함수로부터 얻을 수 있는 점(-b3a, g(-b3a))로 표시되는 변곡점 p의 (x, y)좌표는 표준형에도 그대로 적용될 수 있는 손익분기점 좌표 (x₀, g(x₀))와 같기 때문이다.

결론적으로 f(x) = vx + f라는 실무적으로 확인 가능한 현행의 1차 비용함수를 알 수 있다면, 이로부터 우리가 알고자 하는 장기적 관점의 3차 비용함수는 수학적으로 매우 자연스럽게 g (x) = a(x - p)³ + mx + n 즉, 다음 식으로 도출 가능하다.

3.2 이익극대점과 조업중단점

전통적인 BEP 분석과 달리 3차 비용함수를 통해, 이익극대점과 조업중단점을 확인할 수 있는 비선형 CVP 분석이 가능하다. 확장된 수리모형으로 수익함수 역시 비선형 함수— 예를 들면, 무리함수나 멱함수 등의 형태로 논의를 진행하여야 하나, 비선형 수익함수 도출을 위한 파라미터의 추정은 또 다른 연구 과제이므로, 본 연구에서는 일단 3차 비용함수 만으로 제한적인 비선형 모형으로 분석을 전개한다.

우선 전통적 CVP 분석과 같이 수익함수를 y = x로 전제하면 한계수익함수 y′ = 1이다. 이익극대화 조건은 한계수 익과 한계비용이 일치 y′ = g′(x)하는 것이므로, g (x) = a(x - x₀)³ + vx + f로부터 g′(x) = 3a(x - x₀)² + v, 즉 이익 극대화 조건식은 다음과 같이 구체화된다.

상기 조건을 만족시키는 매출을 구하면,

1-v=3a(x-x0)2

(x-x0)2=1-v3a

x-x0=±1-v3a

x=x0±1-v3a 이다.

이익극대점은 손익분기점보다 커야 하므로 (1-v3a>0), 이익을 극대화하는 매출은 다음과 같다.

전통적 CVP에서 제안하는 단기 목표이익달성 매출액의 계산방식과 달리 3차 비용함수는 장기 목표매출액을 확연하게 제시할 수 있다. 즉 이익극대화 매출액이 최적 매출액이며 단기적으로 실현하기 어렵지만 장기적으로 반드시 달성해야 할 목표매출액이 될 것이다. 결론적으로 본 연구에서 제시하는 3차 비용함수에 의한 이익극대점은 향후 매출예산, 이익예산 등 의사결정에 직접적인 도움을 줄 수 있을 것이다.

조업중단점(downtime point)의 도출 과정은 다음과 같다.

x=a(x-f1-v)3+vx+f

a(x-f1-v)3=(1-v)x-f

a(x-f1-v)311-v=x-f1-v

(x-f1-v)2=1-va

(x-f1-v)=±1-va

x=f1-v±1-va 이다. 따라서 조업중단점은 다음 식과 같이 정의된다.

3차함수의 성질을 이용하면 조업중단점을 구하기 위해 일일이 방정식을 풀지 않아도 쉽게 구할 수 있다. 즉 손익분기점과 이익극대점 차이가 1이라면 손익분기점과 조업중단점 차이는 3의 비례관계를 가지므로 xDTP=x0+1-va임을 쉽게 알 수 있다.

3.3 3차비용함수 곡률의 계산

이제 3차 비용함수에서 개별기업 또는 산업의 특성을 반영하는 것으로 볼 수 있는 중요한 파라미터 즉 3차항의 계수 a를 확정하여야 한다. a는 곡률(curvature)을 반영하는데, 3차 함수의 극대·극소값(α, β)을 알 수 있다면 곡률을 계산하는 일반 공식은 다음과 같다.

그러나 본 연구에서 도출한 3차 비용함수의 경우 극대·극소값이 존재하지 않으므로 이 공식을 적용할 수 없다. 비용함수는 증가함수이므로 모든 점에서 g′(x) > 0이기 때문이다. 따라서 본 연구에서는 3차 함수의 원점에 대한 점대칭성을 이용하여, 변곡점을 원점 이동시킴으로써 곡률을 계산할 수 있음을 보여줄 것이다.

변곡점(x₀, g (x₀))의 원점 (0, 0)이동은 표준형 3차 비용함수의 1차항과 상수항을 다음과 같이 좌변으로 이동시키면 된다.

따라서 원점을 변곡점으로 하는 새로운 3차 함수 h(x)는 다음과 같이 정의될 수 있다.

h(x)의 1계 도함수는 h′(x) = 3a(x - x₀)2이므로 원점에서의 도함수는 h'(0)=3a(0-f1-v)2이고 원점에서의 3차 함수 접선의 기울기도 3차 함수 점대칭성으로 인해 원래 3차비용함수의 변곡접선의 기울기와 같으므로,

h'(0)=v=3a(0-f1-v)2

v=3a(-f1-v)2

a=13v((1-v)f)2이다. 따라서 간단히 요약하면 곡률은 다음과 같이 대수적으로 표시할 수 있다.

이상과 같이 비용함수의 곡률은 변동비율 v와 손익분기점율 x₀에 의해 결정된다는 사실을 확인함으로써, 3차 비용함수를 구체적으로 특정할 수 있다는 것이 본 연구의 실무적 기여점이라 할 수 있다.

4.1 이익함수

이익함수를 도출하기 전, 비용함수가 1차 선형함수 f(x)이든 비선형 함수 g (x)이든 총비용은 같아야 하므로, 즉 비용 제약조건 때문에 vx + f≠ a(x - x₀)³ + vx + f이므로, g (x) = a(x - x₀)³ + vx + k와 같이 상수항을 조정할 필요가 있다.

따라서 총비용은 vx + f = a(x - x₀)³ + vx + k이고 절편은 모든 x에 대해 동일하므로 현재 매출(100%) 기준으로

f(1)=v(1)+fg(1)=a(1-x0)3+v(1)+kv(1)+f=a(1-x0)3+v(1)+kk=f-a(1-x0)3

이다

최종적으로 실무에 적용하여야 할 실질적인 3차 비용함수는 다음과 같다.

그리고 전통적 CVP분석에 의한 이익함수 π(x) = x - vx - f, 즉 π(x) = (1 - v)x - f인 것처럼, 본 연구의 비선형 이익함수 π(x)=x-a(x-f1-v)3-vx-k로부터 다음 식이 가능하다.

단, a=13v(1-vf)2

k=f-a(1-f1-v)3

4.2 이익곡선과 산업라이프사이클

본 연구가 분석적으로 도출한 3차 비용함수에 의한 이익함수의 그래프 즉 이익곡선은 다음 그림과 같이 산업 라이프사이클 이론에서 개념적으로만 간략하게(roughly) 제시하고 있는 이익곡선을 보다 정교한 형태로 구체화할 수 있는 근거가 된다(Grant, 2010; Kyle Peterdy, 2020).

산업 라이프사이클은 기간 경과에 따른 산업의 매출, 이익 그리고 현금흐름의 추이(trend)로 특정 단계(stage)를 설명하는 개념이다. 특히 이익곡선의 행태는 손익분기점 부근의 도입기, 이익극대점까지 도달하기 위한 성장기, 최종적으로 조업중단점으로까지의 쇠퇴기라는 라이프스타일을 설명하고 있다는 점에서 본 연구에서 제시하는 이익함수의 그래프와 밀접한 관련을 갖는다. 산업 라이프사이클 곡선의 한계는 재무적 변수를 시간의 함수로 그리고 있다는 것인데, 현실적으로 이들 변수는 그림과 같이 다양하게 변동한다.

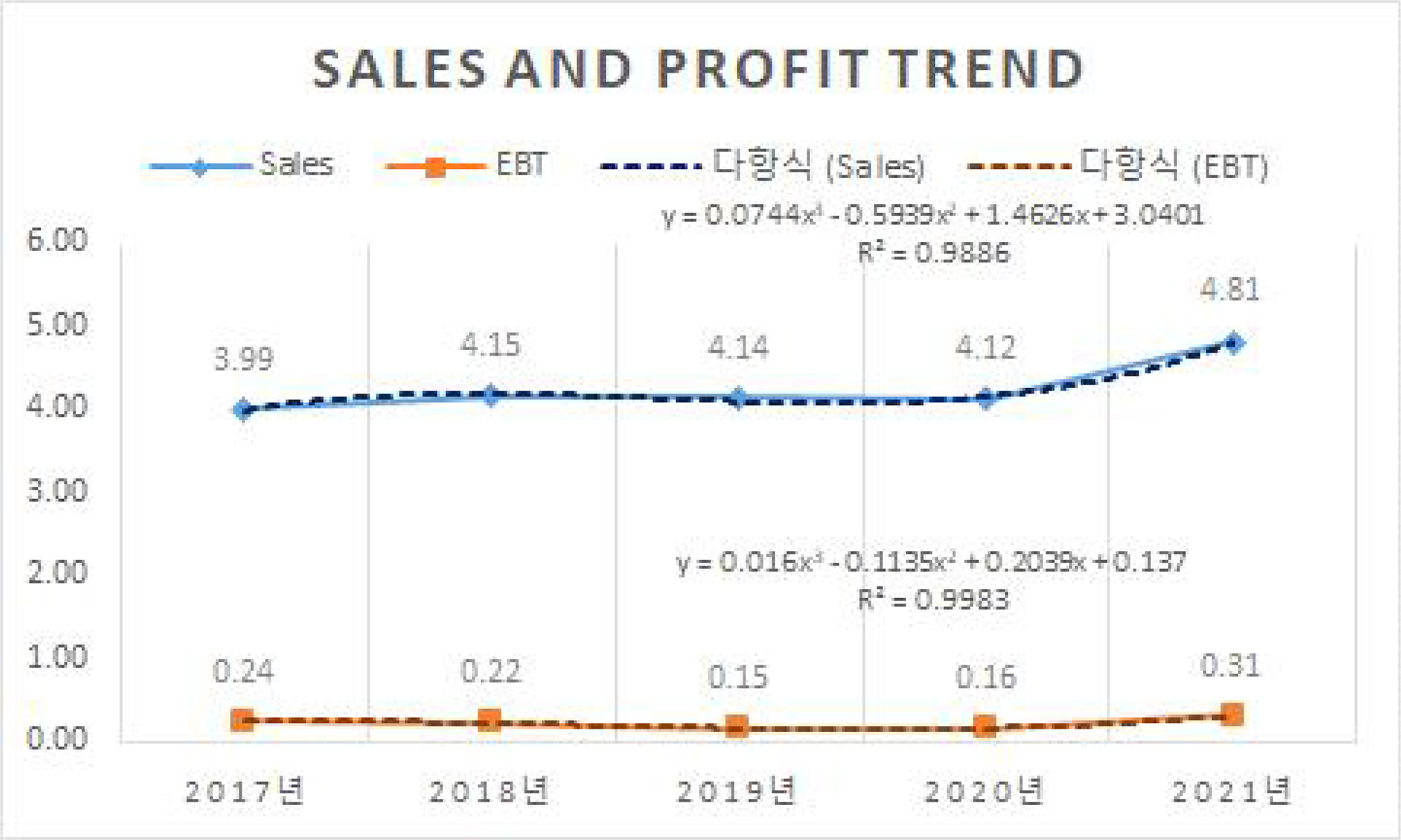
Figure 4는 다음 Table 1의 실제 자료에 기초한 것이다.

Figure 4.

Sales and Profit Trend of All Industries over 5 years in Korea

Table 1.

Sales and Profit of All Industries over 5 years in Korea

Unit(Million KRW)

Figure 4는 우리 나라 전산업의 최근 5년간 매출과 이익의 추세를 보여주고 있으며, 추세가 산업 라이프사이클 상 추세와 대응하지 않고 있다. 따라서 실제 시계열 자료로써 산업 라이프사이클 상 어떤 단계인지 확인하기 어렵다는 문제가 발생한다. 특정 산업이 순차적으로 각 단계를 거치지 않을 수도 있으며, 예컨대 과거 사양산업으로 분류되다가 어떤 계기로 성장산업으로 변화할 개연성은 충분하다. 이처럼 기술 발전, 환경 변화 등 여러 가지 이유로 단계를 역행하거나 어떤 단계에서는 장기적으로 고착화될 경우에, 본 연구에서 제시하는 이익곡선을 통해 산업 라이프사이클 단계를 추론해 볼 수 있다.

다음 표는 한국은행 기업경영분석에서 제시하는 자료로써 우리 나라 전 산업의 2021년 매출액, 세전이익, 변동비율을 이용하여 계산한 이익함수 계수를 요약한 것이다.

Table 2 자료에 의한 구체적인 이익함수는 다음과 같다.

Table 2.

Financial Data of All Industries as of 2021 in Korea and Profit Function Parameters

Unit(Million KRW)

이익함수에 의한 각 좌표는 다음 Table 3과 같다.

Table 3.

Profit Curve Coordinates of All Industries as of 2021 in Korea

Unit(Million KRW)

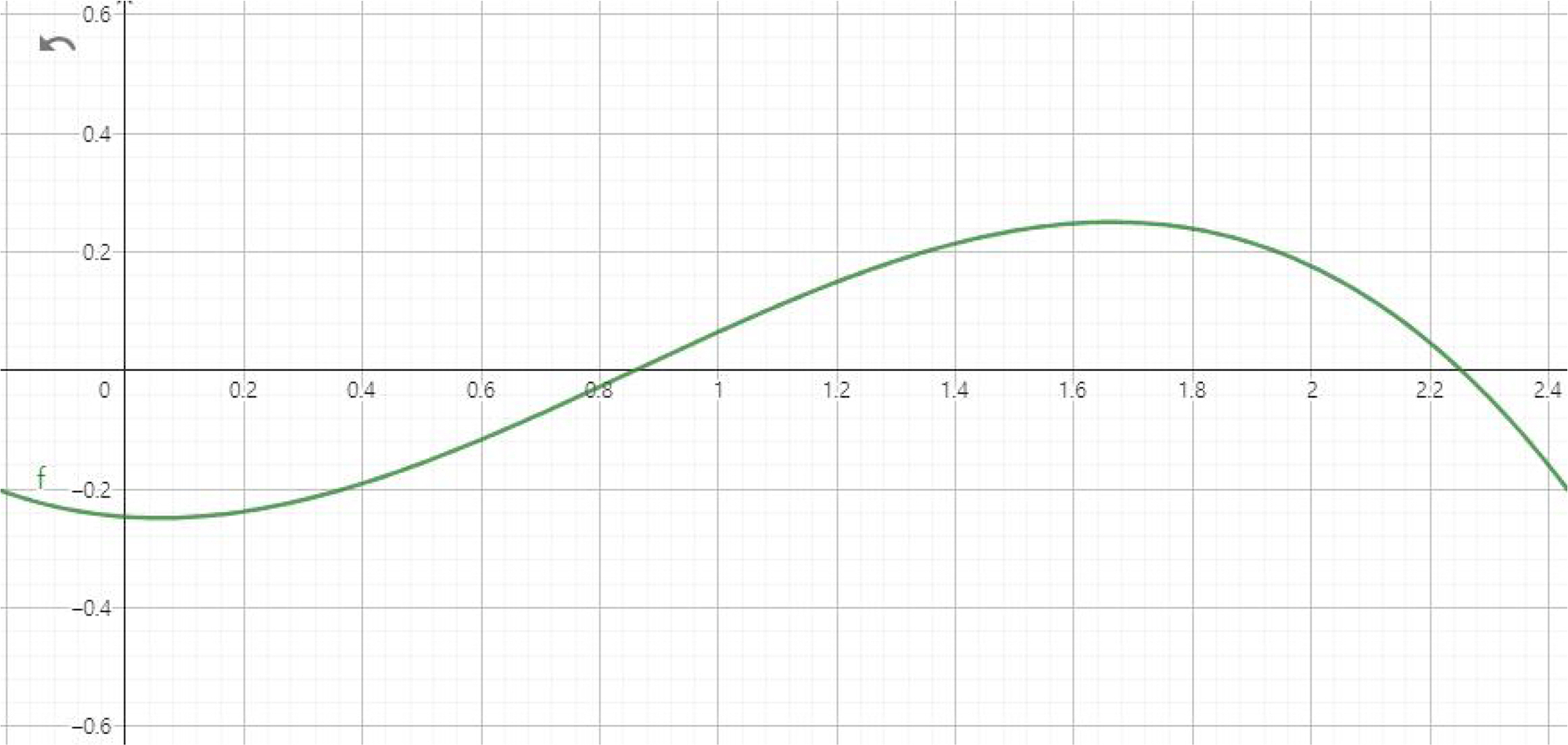
이익함수에 의한 그래프, 즉 이익곡선은 다음 그림과 같다.

Figure 3과 5의 두 이익곡선의 x축이 각각 시간의 흐름과 매출의 증가라는 각각의 차원을 제시하고 있으나, 일반적으로 시간 경과에 따른 산업성장의 결과는 매출증대로 시현된다는 관점에서 같은 맥락으로 보아도 무방하다. 산업 라이프사이클 이론의 주요 논지의 하나는, 도입기로부터 매출증가와 이익증가가 병행(π′(x) > 0)하는 성장기의 정점(π′(x) = 0, 성숙기)을 지나 매출이 증가하더라도 이익이 감소(π′(x) < 0)하게 되는 성숙기 후반 또는 매출 자체가 감소하는 쇠퇴기가 온다는 것인데, 이는 본 연구의 이익곡선 상 손익분기점, 이익극대점, 조업중단점의 진행을 설명하고 있는 것과 같다.

Figure 3.

Industry Life Cycle Curve

Source: https://corporatefinanceinstitute.com/resources/management/industry-life-cycle/

Figure 5.

Profit Curve of All Industries as of 2021 in Korea

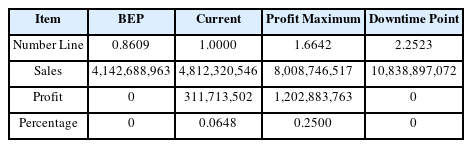
따라서 본 연구의 이익곡선이 산업 라이프사이클의 이익곡선과 유사한 패턴을 보여준다는 관점에서 보면, 우리나라 전 산업의 현재 상태(1, 0.0648)가 손익분기점(0.8609, 0)과 이익극대점(1.6642, 0.2500) 사이에 위치하므로 성장기에 대응함을 직관적으로 알 수 있다.

그러나 이러한 결론이 타당성을 가지려면 이익곡선의 형태를 결정하는 비용구조, 즉 변동비율과 고정비율이 얼마만큼 정확한가에 달려있다. 예컨대 한국은행 자료에서 제시하는 2021년 변동비율 0.5345라는 수치는 비용항목의 성격을 고려한 정성적 판단에 따른 변동비 분류의 결과이다. 다음 식과 같이 순수하게 수학적으로 접근한다면 변동 비율은 달라질 수 있다.

수식에 근거하여 Table 1의 2020년과 2021년 자료에 기초하여 계산되는 변동비율은 0.7817이다

Table 4.

Recalculated Profit Function Parameters

Unit(Million KRW)

비용구조가 달라짐으로 인해 이익함수의 계수 역시 모두 바뀐다.

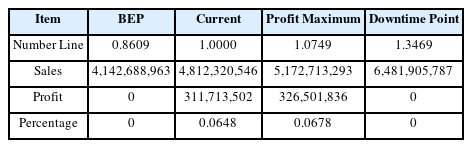
변경된 이익함수에 의한 각 좌표는 다음 Table 5와 같다.

Table 5.

Recalculated Profit Curve Coordinates

Unit(Million KRW)

Table 5에서 볼 수 있는 바와 같이 현재 매출액(1.0000, 0.0648)은 이익극대점 매출액(1.0749, 0.0678)에 거의 근접한 상태이므로 이는 우리 나라 전 산업이 현재 성장기를 지나 거의 성숙기 전 단계(라이프 사이클 이론의 지체기 shake out stage)에 진입했음을 보여준다.

이와 같이 우리나라 전 산업의 라이프사이클이 성장기일 수도 성숙기일 수도 있다는 모호한 검토 결과로 인해, 본 연구의 이익곡선이 산업 라이프 사이클을 제대로 설명하지 못하는 것으로 오해할 수 있으나, 이러한 분석 결과의 차이는 해당 산업의 변동비율 즉, 비용구조를 어떻게 파악하느냐에 달려 있음을 주지하여야 한다.

한국은행이 제시하는 변동비율 산정 방법도 실무적 타당성을 가지며 수학적 접근방법에 의한 변동비율 역시 논리적 타당성을 가지고 있기 때문에 의사결정자는 라이프 사이클 단계 확정에 신중한 주의를 기울여야 한다. 다만 기업 또는 산업의 비용구조는 단기간에 즉각적으로 변경되기 어렵다는 점을 고려하면, 어떤 방식이든 장기적 관점에서 안정화된 변동비율의 적용으로 사고를 전환할 필요가 있다.

다시 말해서, 일 기간만의 변동비율을 일의적으로 적용하여 이익곡선을 추정하기보다 다 기간에 걸쳐 평균변동비율을 산정하고 이를 이익곡선의 추정에 적용하는 것이 신중한 자세로 판단된다. 또한 평균변동비율을 산정하기 위한 기간의 결정은―예컨대 5년 평균변동비율 또는 10년 평균변동비율은 합리적 근거를 가지고 이루어져야 하므로, 이에 대한 동태적 분석 역시 향후 연구 과제가 될 수 있을 것이다. 자료의 수집이 가능하다면 변동비율의 추정을 위해 다기간의 회귀분석에 의한 통계적 접근방법은 가장 합리적인 대안이 될 수 있다.