Article information

Trans Abstract

1. 서 론

다양한 분야에서 해당 분야의 수준을 평가할 수 있는 지수들이 개발되어 경쟁 수준을 비교 평가하는데 유용하게 활용되고 있다. 이러한 지수들은 대부분 직관적인 점수로 표현되어 해당 분야의 전문 지식이 없는 사람들도 그 수준을 쉽게 이해할 수 있다는 점에서 그 활용 범위가 매우 넓다고 할 수 있다.

일반적으로 제품은 설계검증(design verification, DV)을 통하여 기획 및 설계단계에서 요구되는 요건을 만족하였는지를 검증하며, 이는 제품 개발에 매우 중요한 요소가 된다(Seo 2011). 특히, 의도한 사용기간 동안 고장 없이 안정적으로 사용할 수 있는 지 여부를 나타내는 신뢰성 분야에서는 제품이 기획된 높은 신뢰성을 확보할 수 있도록 수명시험, 환경시험, 한계시험 등과 같은 다양한 신뢰성 시험이 수행되고 있다. 일반적인 신뢰성 관리 지표로는 수명시험 또는 신뢰성 예측(reliability prediction) 기법을 바탕으로 산출된 제품의 평균수명, B_p 수명 등이 활용되고 있다. 그러나, 단순 수명시험을 비롯한 개별적인 시험 결과로는 제품 신뢰성 수준을 대표하는데 어려움이 존재한다. 또한, 양산 단계의 제품은 필드에서 수집되는 고장 데이터를 바탕으로 제품의 신뢰성 수준을 평가할 수 있으나, 시장에 출시되지 않은(개발 단계인) 제품은 필드 데이터가 전무하므로 정량적으로 신뢰성 수준을 파악할 수 있는 방법이 요구된다.

이러한 배경에 따라, 본 논문에서는 다양한 스트레스에 따른 필드 고장을 바탕으로 개발된 신뢰성 시험 결과를 종합적으로 고려할 수 있는 신뢰성 지수를 제안하고자 한다. 제안된 신뢰성 지수 모형은 설계, 개발 및 양산 단계에서 얻어지는 정보와 관련 필드 고장확률간의 높은 연관성을 가지는 항목을 선정하여 점수화하고 각 항목별 가중 값을 부여하여 산출하는 모형이다. 이때, 각 가중 값은 최적화 기법을 활용하여 산출된 신뢰성 지수와 제품의 필드 고장확률간에 가장 높은 설명력을 가지도록 설정한다.

신뢰성 지수 모형은 다양한 분야에 적용될 수 있으며, 그 가운데 제품수명주기(product life cycle)가 빠르게 단축되고 있는 스마트폰, 타블릿 PC와 같은 모바일 기기 분야에 매우 유용하게 활용될 수 있다. 그 이유는 모바일 기기는 일반 전자기기보다 사용자에게 노출되는 시간이 매우 높으며, 전화, 카메라, 컴퓨터의 기능이 모두 혼합된 보다 복잡한 구조를 이루고 있어 높은 고장 위험에 노출되어 있다고 할 수 있다. 이처럼 사용자의 일상생활 및 비즈니스에 활용도가 높은 모바일 기기의 고장 발생은 큰 불편을 초래할 수 있게 되고, 사용자의 해당 제품 및 브랜드에 대한 로열티 감소로 이어질 수 있다. 따라서, 본 논문에서는 신뢰성 지수 산출을 위한 모형과 절차를 제안하고 그 활용도가 매우 높은 모바일 기기 분야의 사례연구를 함께 소개하고자 한다.

2. 관련 문헌 연구

신뢰성 지수의 개념을 활용한 연구들은 다양한 분야에서 다수 수행되었다. 먼저, Perera(2006)는 Mobile device 분야에서 시험항목의 필드 고장 재현 정도에 따라 가중 값을 결정하여 합격한 시험항목의 가중 값의 합을 총 시험항목의 가중 값의 합으로 나눈 신뢰성 지수를 제안하였다. 이는 각 시험 항목의 합부 여부만을 토대로 합격 비율을 수치화한 것으로서, 그 외의 정보 등은 활용되지 않았다.

발전 및 전력공급 분야에서는 Melo et al.(1998)이 loss of load probability(LOLP), expected power not supplied(EPNS) 및 loss of load frequency(LOLF)와 같은 신뢰성 지수의 민감도를 도출하는 방법론을 제안하였으며, 브라질의 5개 지역을 대상으로 사례연구를 수행함으로써, 제안된 방법론을 검증하는 연구를 수행하였다. Arya et al.(2012)은 몬테카를로 시뮬레이션을 활용하여 전기 배전 시스템의 신뢰도 지수를 평가하는 연구를 수행하였다.

건축분야에서는 Qin and Zhao(2002)이 RC Beams의 Serviceability limit state(SLS)한 최대 크랙 두께를 신뢰성 지수로 삼아 중국의 콘크리트 구조물 설계기준(China code for design of concrete structures)에 따라 First-order reliability method를 활용하여 도출하는 연구를 수행하였다. 그 밖에, Yoo et al.(2006)은 품질분야에서 KS제품의 종합적 품질지수 측정 도구인 KS-QEI에 대한 실증연구를 수행하였으며, Lim and Park(2010)은 Kano 모델을 기반으로 휴대폰 시장의 고객만족도 향상을 위한 잠재적 고객만족 개선 지수에 관한 연구를 실시하였다.

신뢰성 지수에 관한 다수의 연구가 수행되지는 않았으나, 그 가운데 제품 설계 및 개발, 양산의 데이터를 모두 활용하여 신뢰성 점수를 수치화한 연구는 전혀 이루어지지 않은 실정이다. 따라서, 본 연구에서는 제품 설계 및 개발에서 반영할 수 있는 데이터 뿐만 아니라, 양산 과정에서의 품질 지수를 반영한 새로운 신뢰성 지수를 개발하였다. 또한, 이를 모바일 디바이스에 적용한 사례 연구를 통해 그 효용성을 입증하였다.

3. 신뢰성 지수 개발

3.2 평가 프로세스

본 논문에서는 <Figure 1>과 같이 대상 모듈 선정에서 모델 수립에 이르는 신뢰성 지수 평가 프로세스를 5단계로 구분하여 제안하고 있다.

Figure 1.

Evaluation process of reliability index

1단계는 보증 데이터(Warranty data) 분석을 통하여 지수에 반영할 대상 모듈을 결정하는 단계로서, 이에 앞서 t개월의 필드고장확률, A/S 건수 등 소비자의 체감 신뢰성 수준을 저해하는 관리측도를 선정하여야 한다. 시스템을 구성하는 수많은 모듈에 관한 보증 데이터를 분석하고 이를 모형에 반영하는 것은 매우 어려우므로 파레토 법칙에 의하여 관리측도 측면에서 시스템 대비 높은 비중을 차지하는 모듈을 관리모듈로 선정하여야 한다. 만일 특별히 관리가 요구되거나 전략적으로 신뢰성 지수 모형에 반영하고 싶은 모듈은 위 원칙과 무방하게 반영될 수 있다.

2단계 상관 분석(Correlation analysis)은 관리측도와 각 설계, 개발 및 양산 단계의 다양한 정보간의 상관관계를 분석하는 단계이다. 즉, 관리 모듈로 선정된 모듈의 대상항목 데이터가 우수할수록 필드고장확률, A/S 건수 등이 낮게 나타나는지를 살펴보아야 한다. 만일 항목의 데이터가 우수하여도 필드고장확률과 같은 관리측도가 높게 나타날 경우 해당 시험은 필드고장현상에 대한 설명력이 부족하다고 판단할 수 있으며, 본 단계에서는 이러한 분석을 바탕으로 필드고장현상에 대하여 설명력이 높은 대상항목을 선정하는 단계라고 할 수 있다.

3단계는 2단계에서 선정된 항목의 데이터를 점수화하는 단계이다. 품질지수, 수명 및 한계시험 등으로 구성된 항목들의 데이터는 ppm, 시험시간 및 반복회수 등 독자적인 판정측도 및 기준을 갖는다. 따라서, 이를 하나의 지수로 통일될 수 있도록 경영자 및 분석자의 목적에 따라 점수화 작업이 요구된다. 이를 위해 다양한 함수가 활용될 수 있으며, 예를 들어 선형(linear), 시그모이드(Sigmoid), Power 함수 등이 적용될 수 있다.

4단계는 모델링을 위한 가중 값을 산출하는 단계이다. 가중 값은 수치해석 기법을 활용하여 결정되어야 하며, 이를 위해 최적화 및 휴리스틱 기법이 활용되어야 한다. 이때의 목적함수는 Equation (2)와 같이 모델링에 사용된 제품(입력 제품)들의 신뢰성지수와 관리측도간의 상관관계를 최소화하도록 하여야 하다. Equation (3)과 Equation (4)는 제약조건으로서 모든 항목 가중 값의 합이 1이라는 것과 모든 가중 값은 0보다 커야 한다는 비음조건이 있다. 또한, 분석자에 따라 다양한 제약조건을 삽입할 수 있으며, 특정 항목에 대하여 고정 가중 값을 설정하거나, 가중 값의 상한 및 하한을 설정할 수 있다.

(2) Minimize z=∑i=1nRIi-RIFi-Fn-1sRIsF

(3) Subject to ∑j=1mwj=w1+w2+...+wm=1

(4) wj≥0, ∀ j

이때, RI_i는 i번째 모델의 신뢰성 지수를 의미하며, RI는 전체 관리 모델의 신뢰성 지수 평균을 의미하고 F_i는 j번째 모델의 관리 측도를 의미한다. 또한, F는 전체 관리 모델의 관리 측도 평균을 의미하며, s_RI와 s_F는 각각 전체 관리 모델의 신뢰성 지수 표준편차와 관리 측도 표준편차를 의미하고 n은 총 신뢰성 지수모형에 반영되는 관리 모델의 수이다.

5단계는 결정된 가중 값을 활용하여 신뢰성 지수 모델을 완성하고 이에 입력 제품들의 신뢰성 지수를 산출하여 신규 제품의 관리측도 값을 추정하는 단계이다. 해당 단계에서 신규 제품의 신뢰성 지수도 산출된다. 본 신뢰성 지수 모델은 필드고장확률과 같은 관리측도에 대한 설명력을 극대화하는 신뢰성 지수의 산출을 목표하므로 두 측도간의 선형 회귀 식을 도출할 수 있다. 도출된 선형 회귀 식을 바탕으로 아직 시장에 출시되지 않은 제품의 향후 필드 고장 확률 및 A/S 건수를 예측함으로써, 신뢰성 수준에 대한 정량적인 지표로 삼을 수 있다.

4. 실증 결과분석

본 절에서는 제안하는 신뢰성 지수 프로세스의 적용 방안을 가정된 시나리오를 바탕으로 설명하고자 한다. 또한, 해당 시나리오는 실제 모바일 기기의 설계, 개발 및 양산 정보와 보증 데이터를 바탕으로 실시된 실제 프로젝트에 기반하고 있으며, 보안상의 이유로 일부 수치를 변환 및 삭제하였다.

본 시나리오의 1단계 보증 데이터 분석에서는 신뢰성 관리측도로 12개월의 필드고장확률을 선정하였으며, Nevada chart 형태로 수집되는 A/S 데이터를 바탕으로 필드고장확률을 추정하였다. Nevada chart란 보증 데이터를 수집하는데 활용되는 표 양식으로서, 제품의 판매(생산) 시점 별 경과 기간(일, 주, 월, 년 등)에 따른 고장 데이터를 기입하는 형태로 <Figure 2>와 같다. 본 연구에서는 해당 양식의 필드데이터를 분석하기 위하여 신뢰성 분석 소프트웨어인 Weibull++ 9의 Warranty analysis folio 기능을 활용하여 분석을 수행하였다.

Figure 2.

Example of a nevada chart

모바일 기기는 Main board, I/F connector, LCD, Battery, TSP(Touch screen panel), Camera, Speaker 등을 비롯한 수많은 모듈로 구성되어 있다. 먼저 모바일 기기를 구성하는 다양한 모듈들의 필드고장확률에 대한 파레토 분석을 실시하여 모바일 기기의 전체 필드고장에 높은 비율을 차지하는 모듈을 도출하였으며, 해당 순위는 아래 <Table 1>과 같다.

Table 1.

Module Ranks of mobile devices in sorting high field failure probability

<Table 1>을 살펴보면, Main board, I/F Con., LCD, TSP 모듈이 6개 모델에서 동일하게 상위 4종 모듈에 포함된 것을 확인할 수 있다. 단, Model 4의 경우 TSP 모듈이 Rank 5에 해당되어 위 <Table 1>에 포함되지 않았다. 또한, 위에서 언급된 4종 모듈의 필드고장확률의 합은 제품의 필드고장확률의 최대 84 %를 차지하는 것으로 나타났다. 따라서, 본 연구에서는 LCD와 TSP를 디스플레이 관련 모듈로서, LCD 모듈로 관장하여 Main board, I/F Con., LCD 모듈을 관리모듈로 선정하였다.

2단계는 1단계에서 선정된 3종 모듈에 대하여 모듈의 필드고장확률과 수명 및 한계시험 결과간의 상관분석을 실시하였다. 수명 및 한계시험은 망대특성을 가지는 시험결과를 나타내므로 망소특성인 필드고장확률과 강한 음의 상관관계를 보일수록 높은 설명력의 시험항목이라 할 수 있다. 다양한 시험항목별 결과와 필드고장확률간의 상관분석 결과, 모듈 별 가장 강한 음의 상관관계를 갖는 2종의 시험을 선정하였으며, 선정된 시험의 상관계수는 아래 <Table 2>와 같다. 반면, 신뢰성시험을 제외한 품질지수, 디레이팅 및 제조사에서 독자적으로 관리하는 데이터도 함께 필드고장확률과의 상관분석을 실시하였으나, 상관관계가 미미하여 제외하였다.

Table 2.

A result of correlation analysis for selected tests of each module

본 연구에서는 앞서 선정된 시험항목의 결과를 점수화하기 위해 시그모이드 함수를 적용하였으며, Equation (5)와 Equation (6)과 같다. 시그모이드 함수를 적용한 이유는 일정 수준에 도달할 때까지는 점수의 상승 폭이 높고 높은 점수 구간에서 상승 폭이 감소하는 위로 볼록한 형태의 함수를 적용하기 위하여 선정하였다. Equation (5)는 각 시험항목의 모델별 시험결과에 따라 0점부터 100점까지 부여하는 시그모이드 함수로서, 상수 α와 s_ij에 의하여 점수 커브를 결정하게 되며, Equation (6)의 s_ij는 각 시험항목의 평가 기준 χ'_j와 실제 결과 χ_ij의 비율을 의미한다.

이때, χ_ij는 i번째 모델과 j번째 시험항목의 시험결과를 의미하고, χ'_j는 j번째 시험항목의 평가기준을 의미한다. 상수 α는 s_ij가 1일 경우 기준 점수를 결정하는 상수로서, 본 연구는 기준점수를 70점으로 설정하여 α를 1.735로 가정하였다. 이와 같은 시그모이드 함수를 활용하여 각 모델의 시험 항목별 점수, s_ij를 산출한 결과는 아래 <Table 3>과 같다.

Table 3.

Calculated scores for each model and test by the sigmoid function

다음으로 각 시험항목의 가중 값을 결정하여 신뢰성 지수를 산출하여야 한다. 본 논문에서는 앞서 3장에서 소개된 목적함수 및 제약조건에 따라 비선형계획법(Non-linear programming)을 적용하여 가중 값을 최적화하였으며, 그 결과는 아래 <Table 4>와 같다. 또한, <Table 4>의 가중 값을 바탕으로 수립된 신뢰성 지수 모형은 Equation (7)과 같다.

Table 4.

Optimal weights of each test by a non-linear programming

도출된 가중 값 결과에 따르면, 신뢰성 지수에 가장 큰 영향을 미치는 모듈은 LCD이며, 다음으로는 I/F Con., Main board 순으로 신뢰성 지수에 영향을 미치는 것으로 분석되었다. 가장 높은 영향력을 보이는 시험 항목은 LCD의 Test 6로 나타났으며, Test 2와 Test 5는 가중 값이 0으로 신뢰성 지수에 반영되지 않는 것으로 분석되었다.

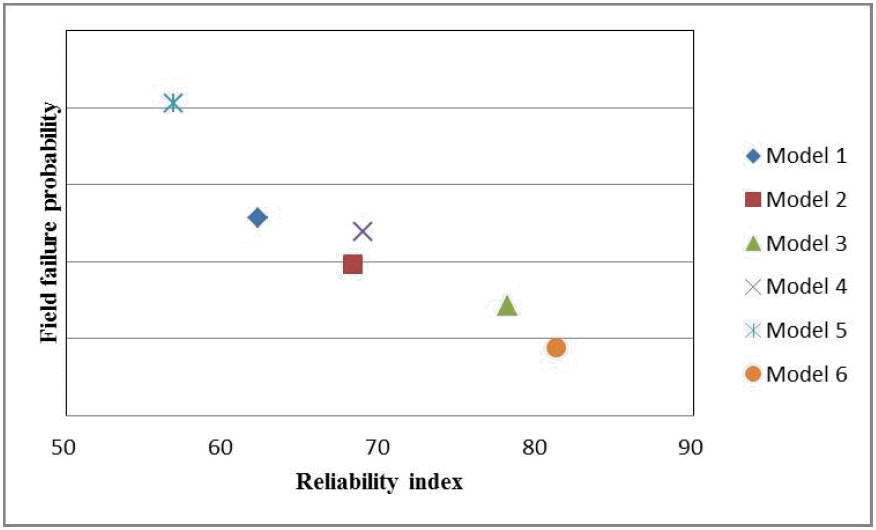
이에 따라 수립된 신뢰성 지수 모형에 시험항목 별 점수를 대입하여 각 모델 별 신뢰성 지수를 산출할 수 있으며, 이를 필드고장확률과 상관분석을 실시함으로써, 모델의 설명력을 평가할 수 있다. 각 모델 별 신뢰성 지수는 아래 <Table 5>와 같으며, 산출된 신뢰성 지수와 필드고장확률간의 상관계수는 -0.9505로 분석되었다(<Figure 3> 참조).

Table 5.

Reliability index of each model by a proposed method

Figure 3.

A x-y plot for reliability index and field failure probability of each model

5. 결 론

기존 제품들의 신뢰성 지표는 통계적으로 설계된 보증시험 및 수명시험 결과에 의한 제품 수명(평균수명, B_p 수명 등)으로 관리되어 왔으며, 보다 높은 신뢰성을 갖는 제품을 개발하기 위하여 무조건적으로 높은 수준의 제품 수명을 위한 설계 및 생산이 이뤄져 왔다. 그러나, 과거와 달리 제품 수명 주기가 단축됨에 따라 신제품의 출시 간격도 함께 단축되어 기존의 높은 수명을 추구하던 방식에서 설계적 시간 및 비용 측면을 고려하여 효율적인 목표 수명 달성을 위한 개발 및 설계가 요구되고 있다. 특히, 이러한 경향은 모바일 기기 시장에서 보다 두드러지게 나타나고 있으며, 빠르게 단축되는 수명주기만큼 제품의 교체주기도 점차 빨라지고 있다.

이에 따라, 기존의 신뢰성 지표인 수명을 대신하고 개별적으로 관리되던 다양한 신뢰성 시험 결과를 바탕으로 제품의 신뢰성 수준을 종합적으로 관리 및 비교 평가할 수 있는 지표가 요구되고 있다.

이를 위하여, 본 논문에서는 제품의 설계, 개발 및 양산 단계에서 얻어지는 다양한 데이터를 대상으로 필드고장확률, A/S 건수와 같은 필드데이터와 비교 분석을 실시하여 필드고장현상을 잘 설명하는 대상항목을 도출하고자 하였으며, 이를 바탕으로 제품간의 정량적인 신뢰성 수준을 평가하기 위한 신뢰성 지수 모델을 제안하였다.

이러한 신뢰성 지수 모델을 도입할 경우 기대되는 효과는 다음과 같다. 첫 번째, 개발단계에서 신규 제품의 필드 신뢰성 수준을 미리 추정(예측)할 수 있다는 것이다. 필드고장현상에 대한 설명력이 높은 항목을 선정하고 필드 신뢰성 수준과 가장 높은 상관관계를 갖도록 가중 값을 설정함으로써, 신뢰성 시험 결과와 같이 양산단계 이전에 얻어지는 데이터를 바탕으로 신규 제품의 향후 필드 신뢰성 수준을 미리 예측할 수 있으며, 기존 제품과의 개발 완성도를 비교 평가해 볼 수 있다.

두 번째, 대상항목의 필드 고장 설명력을 평가하여 해당 중요도를 판정할 수 있다. 제품의 신뢰성과 관련있을 수 있는 다양한 데이터 중 필드고장현상 및 관리지표에 대한 설명력이 높은 항목을 선정함으로써, 신뢰성 향상을 위한 우선 개선 항목을 도출할 수 있다. 또한, 설명력이 부족한 항목은 제거하거나, 신뢰성 시험의 경우 해당 시험조건 및 기준을 개선함으로써, 보다 유효한 시험이 이뤄질 수 있도록 할 수 있다.

세 번째, 계속적인 신뢰성 향상을 위한 동기를 부여한다. 기존의 기준요건을 통과하면 합격이라는 단순 관리 방식에서 벗어나 미흡한 신뢰성 지수 항목을 향상시키기 위한 동기를 부여함으로써, 지속적인 신뢰성 개선활동을 수행할 수 있다.

마지막으로 추가적인 항목에 대한 효과를 확인할 수 있다. 필드 데이터를 바탕으로 취약 부분을 보완하거나 신규 제품을 위해 개발된 추가적인 신뢰성 시험이나 새로운 데이터를 신뢰성 지수 모델에 반영함으로써, 도출된 신뢰성 지수를 통해 개선 효과를 파악할 수 있다.

Article information Continued