2.1 신뢰성 개념

MIL-STD-721에서는 신뢰성을 다음과 같이 정의한다. 신뢰성은 제품이 주어진 사용조건 아래서 의도하는 기간 동안 정해진 기능을 성공적으로 수행하는 능력 또는 성질이며 신뢰도로 표현을 한다. 신뢰도는 시스템이나 제품의 성능이 지닌 시간적 만족도로서 부품이나 시스템이 주어진 조건하에 규정된 기간 중 요구되는 기능을 수행할 확률로 정략적 표현이라 보면 된다.

신뢰성의 개념은 제 1차 세계대전 중 다수의 전자장치에 고장이 발생하였는데, 이것을 수리하고 유지 보수하는데 지출되는 비용이 초기비용에 비하여 훨씬 많았기 때문에 이것을 실질적으로 어떻게 해결해야 할 것인가 하는 필요성에서 신뢰도의 개념이 발전하게 되었다.

신뢰성은 품질에 시간의 개념을 포함한 의미이다. 공장 출하의 품질도 중요하지만 시간이 지난 후의 품질도 중요하다고 판단되기 시작했고, 시간이 지난후의 품질을 신뢰성이라 부른다.

유도탄의 경우 초기고장기간에 초도생산기간 및 공장출하직전에 품질문제로 인해 고장률이 높게 나타날 수 있지만 ESS나 환경시험, Burn-in등을 통하여 초기고장률을 낮출 수 있다. 하지만 납품이 되어 저장을 하는 우발고장단계부터는 고장률이 매우 안정적인 분포를 보이게 된다. 우발 고장기간이 상대적으로 매우 긴 것이 유도탄의 특징이지만 ,현재 00유도탄의 경우 4년 주기로 주기점검을 설정하고 있다. 본 논문에서 제시하고자 하는 부분이 주기점검을 4년마다 시행하는 것을 양산단계 신뢰도분석을 통하여 점검주기 연장하는 것이다.

2.2 관련 이론

이종문 외 2명 (2011)은 OO 무기체계에서 고장율을 산출하는 연구를 수행하였다. 유도탄의 신뢰도를 유지하기 위해서는 예방점검주기가 필요하다고 판단하였고 이에 대해 얼마 주기로 예방점검을 수행하여야 하는지에 대해서 분석을 하였다. 결과는 5년 미만의 예방점검주기는 30년이상 저장신뢰도가 90%이상 유지되는 것으로 나왔지만 6년을 초과하여 설정한 예방점검주기는 신뢰도가 90%이하가 나오는 것으로 분석되었다. 즉 5년 수명점검주기에 30년 수명이 적정하다고 제시하였다.

김동규 외 2명 (2013)은 일회성 시스템의 저장신뢰도 결정모델에 관한 연구를 수행하였다. 시스템 고장시간이 지수분포를 따를 경우 저장신뢰도모형을 제시하여 저장신뢰도 모형을 제시하여 Martinez 검사모형과 비교하였고, 또 고장시간이 와이블분포나 감마분포를 따를 경우 저장신뢰도를 만족할 수 있는 최적 검사주기를 제시하였다.

무기체계의 운용수준이 높아지면서 시험평가에 대한 중요성이 계속해서 증가하고 있다. 박종완(2015)은 시험평가 과정의 신뢰성을 향상시키기 위해 시험평가 분야의 전문가 그룹을 통해 신뢰성에 영향을 미치는 내외부 요인 중 우선순위를 도출하였고 개선방안을 제시하였다. 시험평가 전문화, DT/OT 전환을 위한 검증체계정립, 내구성 환경시험에 대한 인식제고, 시스템엔지니어링 등 과학적 시험평가 기법 적용, 시험평가 적정 시제수, 시험평가 업무의 표준화 정립이 된다면 시험평가 신뢰성이 높아질 수 있다고 보았다.

조일훈(2014)은 필드데이터를 활용하여 고장률 산출하는 연구를 수행하였다. 연간 운용 시간, 양산후 전력화배치 수량, 개발 MTBF, 필드 고장데이터를 이용하여 불량률을 산출하였다. 필드데이터 분석 시 가정을 하였는데 납품일과 고장접수일간의 차이를 운용기간으로 산출하였다. 또한 고장접수가 되지 않는 장비에 대해서는 고장률에 반영이 되지 않는다고 가정하였는데 이는 필드데이터의 한계점이라 판단된다. 하지만 이정도의 데이터를 구하기도 쉽지 않을 뿐만 아니라 제대로 관리되지 않은 필드데이터도 많기 때문에 어느 정도의 가정 사항은 포함되어야 한다.

김희욱 외 4명은 (2014) 수중유도무기체계의 신뢰도 할당에 관한 연구를 수행하였다. 신뢰도할당연구는 여러 가지 기법을 비교하여 최적의 할당법을 찾아내는 것이지만 그 기본이 되는 자료에 고장률이 포함되어있다. 특히 ARINC 배분법에는 고장률이 반드시 포함되게 되어있으며 고장률을 근거로 하여 각 부품 신뢰도를 할당하게 된다. 이런 신뢰도 할당 값은 체계목표 신뢰도를 달성하기 위한 설계지표로 사용되며, 여러 부품으로 이루어진 유도탄의 신뢰도 분석에 유용하다고 판단된다. 또한 국방 분야에서는 고장률분석을 통해 저장신뢰도 예측하는 분야의 연구가 활발히 일어나고 있다. 조용석, 박대현은 (2001) 변환계수법(conversion Factor Method)를 활용하여 유도탄의 저장신뢰도를 예측하였다. 비 운용상태에서 신뢰성 예측의 필요성을 최초로 제기한 사람은 Bazovsky, Igor로 1961년에 체계신뢰도 계산 시 비 운용상태에서의 신뢰도를 “quiescent” 신뢰도로 정의하였다.

하지만 기존논문에서는 기존에 나와 있는 고장률을 산출하여 신뢰도를 구하는 방법론을 대부분 사용하고 있지만 본 논문에서는 사격결과, 주기점검 결과의 이산적 결과(정상, 고장)을 가지고 접근하였으며 유도탄의 고장에 대한 개념을 정립했다는 것에서 기존 논문들과 차별성을 가지고 있다고 판단된다.

3.1 데이터 수집 및 가정

00 유도탄에 대한 저장 신뢰도를 추정하기 위해 전력화 배치 이후 최근까지 육군과 방산제조업체에서 몇 년간의 납기실적 및 사격결과, 주기검사 결과를 수집하였다. 수집된 자료는 00년 양산 이후 납품 실적 및 주기검사 결과, 사용 내역이다. 세부적인 고장데이터는 군사보안과 연관이 있으므로 분석에만 활용하였고 비공개로 처리하였다.

납품수량은 00년 양산 이후 군에 납품한 실적을 의미한다. 납품은 대부분이 매년 연말에 납품되고 또 보안과 연관이 되기 때문에 12월 30일로 가정하였다. 또한 관측중단 시점은 16년 5월 30일로 가정하였다. 사격시험 결과를 확인하는 시점과 주기검사를 시행한 시점을 유도탄의 수명이라고 가정하였다.

가장 중요한 부분은 고장이라고 판단하는 기준이다. 유도탄의 경우 군 납품이후 운용되지 않고 저장만 한다. 아무것도 건드리지 않는 상태를 의미한다. 본 논문에서는 2가지 가정을 한다.

첫 번째는 유도탄의 고장은 사격 시 불 명중을 하였거나 미발사가 되었을 때 기타 기인이 아닌 유도탄기인으로 판명되었을 경우이다. One Shot System의 특성상 사격을 해봐야 성능이 입증이 되기 때문에 고장데이터에 반드시 포함될 필요가 있다.

두 번째는 주기적인 검사를 시행할 때 전기적 성능 값이 정상규격범위를 벗어났을 경우이다. 주기적 검사는 4년마다 군에서 실시하는 검사인데 일정시간이 지난 유도탄의 대해서 전수로 진행하고 있다. 무기체계마다 주기는 다를 수 있지만 주기검사를 진행하는 것을 원칙으로 하고 있다. 그래서 주기적인 검사 때 전기적 성능 값이 정상범위를 벗어난 것에 대해서는 사격 시 불 명중 혹은 미 발사 될 가능성이 높다고 판단했고 고장이라고 가정하였다.

그리고 그 외에 ASRP (Ammunition Stockpile Reliability Program)도 유도탄의 고장유무를 판단할 수 있는 근거가 되지만 현재 ASRP 주기에 도래한 무기체계가 소량이라 본 논문 분석에서는 제외하였다.

본 논문의 유도탄 고장 데이터는 유도탄의 저장연수와 납품된 유도탄의 수, 불량으로 판정된 유도탄 개수의 형태로 구성될 수 있고 각 저장연수에 대해 다수 회 관측된 계수적 반응 자료에 속하므로 유도탄 저장연수를 설명변수로 간주하여 프로빗(Probit) 분석을 수행하였다.

3.2 프로빗(Probit) 분석

연령이 x_i(i=1,2,⋯,n)인 시전에서 n_i개의 유도탄을 시험 발사하거나 주기검사를 하였을 때 j(j=1,2,⋯,n_i)번째 유도탄이 고장이 나면 Y_ij=1, 고장이 나지 않으면 Y_ij=0이라 하자. 이 때 종속변수는 이항변수이기 때문에 베르누이 분포(Bernoulli Distribution)를 기초로 하는 프로빗 모델을 사용한다.

여기서, 관찰되어지지 않은 임의의 변수 Yij*는 하나의 분계점(μ=0)을 가지며, 다음방정식 (1)을 만족시킨다.

이 때 u_ij는 오차항으로 적절한 분포를 따른다고 가정한다. 보통 u_ij가 평균이 0이고 표준편차가 σ인 정규분포 N(0,σ²)를 따른다고 가정하고, 이 모형을 프로빗 모형이라 한다. 오차항이 정규분포를 따를 때, 연령이 x_i인 유도탄이 고장날 확률을 π_i라고 하면 고장날 확률 π_i는 다음과 같이 계산할 수 있다.

다만, z=β0+β1xi, ɸ(z)=12π∫-∞ze-t22dt는 표준정규분포의 누적분포함수(Cumulative Distribution Function, CDF)를 나타낸다. 또한 오자항의 분포에 따라 누적분포함수가 달라지므로 이를 프로빗 모형의 연결함수 (Link function)이라고 한다.

신뢰성 이론에서는 정규분포보다는 대수정규분포(Lognormal), 와이블(Weibull), 로지스틱(Logistic), 대수로지스틱(Loglogistic) 등을 더 많이 사용한다. 따라서 본 논문에서는 위 4가지 분포를 바탕으로 프로빗 분석을 실시하였다.

3.3 모형의 타당성 검정과 모형 선택

앞 절에서 사용하는 모형에 따라 유도탄의 신뢰도는 다르게 추정된다. 이때 사용하는 모형이 적절한 모형인지 타당성을 검정하거나 모형을 선택하기 위해 사용하는 것은 이탈도(deviance)와 피어슨(Pearson) 잔차를 사용한다.

이탈도는 Hosmer and Lemeshow(2000)이 제안하였으며, 다음 식 (3)과 같이 정의 된다.

단, n_i는 연령이 x_i에서 시험되는 유도탄의 수, y_i는 n_i개 중 고장 난 것의 개수, 즉, yi=∑j=1niyij이다. 또한 Pearson 잔차는 다음 식 (4)과 같이 정의 된다.

Pearson 잔차 또한 χ²(n-k-1)분포를 이용한 적합도 검정 결과를 얻을 수 있다.

4.1 적합분포 선정

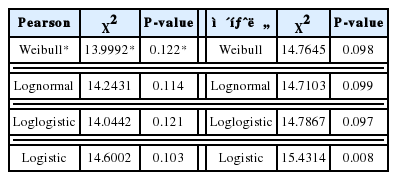
적합한 분포를 찾기 위해 이탈도와 Pearson 값을 이용하여 비교해 보았다. 만약에 검정통계량의 P 값이 유의수준 0.05보다 작다면 가정된 분포에 적합하지 않다고 볼 수 있다. <Table 1>에 나와 있는 네 가지 분포 (Weibull, Lognormal, Loglogistic, Logistic) 를 비교해보면 Pearson 검정통계량이 가장 작은 Weibull 분포와 이탈도 검정통계량이 가장 적은 Lognormal 분포가 다른 분포에 비해 이 데이터에 적합하다고 볼 수 있다. 하지만 P-value 값을 비교하였을 때 Pearson 검정통계량이 값도 낮고 P-value 값이 더 높으므로 Weilbull 분포가 가장 적합하다고 판단하였다.

Table 1.

Pearson, Deviance Statistic and P-value comparison

4.2 회귀계수 추정

와이블 분포를 이용하여 프로빗 분석을 한 결과, <Table 2>를 보면, 설명변수 계수 β₁은 4.658 상수계수 β₀는 -13.993 으로 추정되었는데 P값이 0.000 으로 나와서 모두 유의하다고 판정할 수 있다. 다음 식으로 계수적 반응 자료에 대한 회귀모형을 정식화 할 수 있다.

Table 2.

regression model of probit analysis

4.3 백분위수 추정

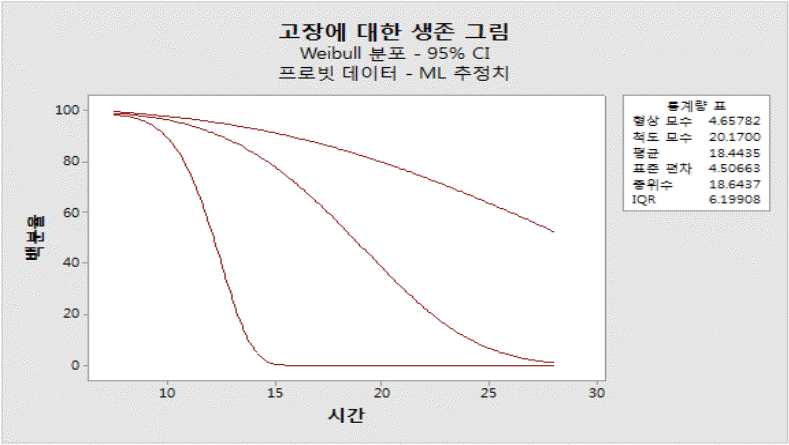
프로빗 분석에서는 백분위 수 분석 결과를 제공하고 있고 이에 따라 백분위율에 따른 저장수명을 추정할 수 있다. 가장 많이 사용하는 제 10 백분위 저장수명을 추정해보았다. 아래 <Table 4>에 따르면, 10 백분위 저장수명은 12.442년으로 추정할 수 있으며, <Table 3>에서는 신궁 유도탄의 Weibull 수명분포의 형상모수는 4.658, 척도모수는 29.170로 추정된다고 분석되었다.

Table 4.

percentile estimation and life estimation

Table 3.

shape parameter and scale parameter of Weibull distribution

4.4 년도별 신뢰도 분석

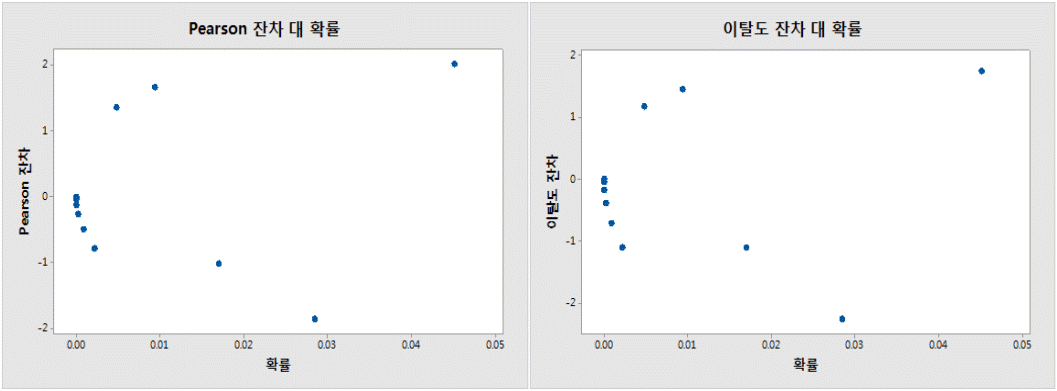
Weibull 분포를 적용한 프로빗 분석결과 <Table 5>를 살펴보면 저장연수가 5년일 때는 생존확률 0.998, 10년일 때는 0.962, 15년일 때는 0.777, 20년일 때는 0.382로 추정되었다. 이를 토대로 예측해보면 유도탄의 저장되고 10년 동안은 고장확률이 낮은 편이라고 분석된다. 하지만 10~15년 사이에 고장확률이 낮아지기 시작하고 15~20년 사이에서는 급격히 낮아지고 있다. 소요군이 요구하는 신뢰도 0.8은 14.6년에 도달한다고 추정되나 하한값 기준으로 봤을 때 11년에 신뢰도 0.8 이하로 떨어지는 유도탄이 발생된다고 추정할 수 있다. 주기검사가 4년으로 설정되어있는데 유도탄의 저장연수별 고장확률을 봤을 때 검사 주기의 중요성을 다시 한 번 강조할 수 있으며, 주기검사, 사격 시험 등 저장수명을 가지는 유도탄의 수명을 분석할 수 있는 사전 확인 작업이 체계적으로 개발되어야한다고 판단된다. <Figure 1>은 고장에 대한 생존확률을 나타내고 있다. 또한 <Figure 2> Pearson 잔차와 이탈도 잔차가 거의 일치하는 것을 확인할 수 있다.

Table 5.

survival probability

Figure 1.

Survival function of Weibull distribution

Figure 2.

Pearson, Deviance residual of Weibull distribution