Article information

Trans Abstract

1. 서 론

컨조인트 분석은 마케팅분야에서 신제품(또는 서비스) 개발과 관련하여 많이 활용되는 기법으로 Luce와 Tukey (1964)에 의해 처음 소개 되었고 김부용(2005)에 사례분석을 통해 예시되었다. 특정 제품을 구성하는 각 속성들의 취하는 값들을 인위적으로 변경하며 결정된 다양한 제품들에 대한 소비자들의 종합적인 선호도 조사 결과들을 토대로 특정 제품을 구성하는 각 속성들의 취하는 값인 수준들이 결정된 경우에, 해당 제품에 대한 평균 선호도를 추정하여 소비자들이 실제로 신제품이 출시되었을 경우에 구매할 가능성이 높은 제품을 예측할 수 있기 때문에 마케팅 분야에서 신제품 개발과 관련하여 많이 활용된다. 본 연구에서 선호도는 점수조사인 경우를 가정한다.

컨조인트 분석은 신제품을 구성하는 속성들과 그의 수준들의 결합들로 후보 신제품에 해당하는 문항들 즉 컨셉을 만들어 소비자들의 종합적인 선호도를 조사하여 분석하는 기법이다. 컨셉을 구성하는 방법은 속성들의 수준 결합을 처리(treatment)로 간주하여 실험계획법의 실험점 생성 방법을 적용하는데 고전적 방법에 의하면 속성들의 주효과에만 관심을 두어 설문지 문항들을 설계한다. 그러나, 임용빈(2015)에서도 언급하였듯이 마케팅 실무 담당자들의 가장 큰 관심사는 속성들간의 시너지 효과 혹은 적대적(상충적)인 효과의 존재 여부를 파악하는 것이다. 그래서, 임용빈(2015)에서는 속성별 수준수가 모두 동일하다는 가정 하에 응답자를 블록으로 간주하여 응답자에 대한 설문지 문항들의 설계를 균형된 불완전 블록 완전요인설계(Balanced Incomplete Block Full Factorial Design)이거나 해상도가 V인 균형된 불완전 블록 일부요인설계(Balanced Incomplete Block Fractional Factorial Design)의 방법들을 활용하여 모든 이인자 교호작용 효과의 추정이 가능하도록 설계하였다. 그러나, 현실적인 문제에서는 항상 수준수가 동일할 수는 없을 것이다. 속성별 수준수가 다른 경우에는 어떤 방식으로 문항들을 설계할 수 있는지 이 논문을 통해 제안하고자 한다.

실험계획법에서는 수준수가 다른 속성들의 실험점 생성을 혼합수준 요인설계(mixed level factorial designs)라고 하는데 Wu & Hamada (2011)에 잘 정리되어 있다. 일반적인 혼합수준 요인설계 방법으로는 동일한 수준수별로 각각 실험점들을 설계한 후 결합하는 것이다. 예를 들어, 2수준 2개의 속성과 3수준 2개의 속성인 2² × 3² 완전요인설계(Full Factorial Design)를 하기 위해서는 2² 인 실험점 4개와 3² 인 9개를 각각 설계한 후 2수준 속성들로 구성된 각각의 실험점에서 3수준 속성들로 구성된 3² 실험점 9개를 결합하여 실험을 실시한다. 즉, 2² 실험설계와 3² 실험설계의 교적설계인 총 36개의 실험점을 생성하도록 하는 것이다. 속성들의 수가 많아질 경우에는 임용빈(2015)의 방법을 적용하면 동일한 수준수별로 균형된 불완전 블록 완전요인설계(이하 블록화 완전요인설계)나 해상도가 V인 균형된 불완전 블록 일부요인설계(이하 블록화 일부요인설계)를 구한 후 결합하는 블록화 혼합설계를 하면 된다.

블록화 혼합설계를 활용한 설문지 문항들의 설계는 블록이 응답자가 되고 블록에 배치된 실험점들이 그 응답자에 대한 설문 문항들이 된다. 응답자가 공정하게 평가할 수 있는 문항들의 개수의 한계를 반영하여 설문지 문항의 수인 블록의 크기와 총 응답원들의 수에 해당되는 블록의 수를 결정한다. 속성들의 수가 많은 경우, 모든 이인자 교호작용효과를 추정하기 위해 각 블록과 교락될 교호작용효과는 삼인자 이상이어야 하기에 블록의 수는 적어지고, 블록의 크기인 응답자가 응답해야할 설문 문항수가 많아져서 응답자로부터 정확한 답변을 기대하기가 어렵게 된다. 이러한 경우, 블록 당 문항수를 줄이기 위해서는 블록의 수를 많게 해야 하기에 불가피하게 블록과 교락될 일부 이인자 교호작용효과를 허용해야 하고, 이 교호작용효과는 추정이 불가능하게 된다. 이 경우에 이인자 교호작용효과 중 일부의 추정 불가능을 허용하되 그것의 개수를 최소로 하는 블록화 혼합설계 방법을 고려한다. 또한, 속성들의 수준수를 모두 동일하게 맞추어 블록화 요인설계를 하는 방법도 고려한다. 예를 들어, 앞에서 설명한 2² × 3² 혼합설계에서, 3수 준 속성을 2수준 속성 2개로 표현하여 속성들이 모두 2수준인 2⁶ 설계인 것처럼 실험점을 생성하든지 2수준을 3수준 속성으로 표현하여 속성들이 모두 3수준인 3⁴ 설계인 것처럼 실험점을 생성하여 문항 설계를 한다.

이 논문에서는 속성별 수준수가 2와 3인 2^f × 3^g 혼합설계를 다루며 주어진 컨셉 혹은 실험점에 대한 응답자의 반응값은 선호도에 대한 점수로 9점 척도로 가정한다. 실무 담당자들의 궁극적인 목표는 효율적인 컨셉 최적화를 수행하기이다. 이를 위해서는 간단하고 적절한 설문지 문항 자료의 분석을 통해서 반응변수인 선호도(혹은 구매의사 점수)와 속성과 관련된 요인 효과들 간의 적절한 모형을 찾는 것이다. 이를 위해 요인효과들의 반정규 확률그림을 통하여 핵심적인 효과들을 시각적으로 우선 선별하고, 모형 평가 통계량의 비교를 통해서 모형들의 예측력을 비교하고, 잔차분석을 통해서 선별된 모형의 적절성을 확인한다. 효율적인 컨셉 최적화는 선택된 적절한 모형에 대해서 반응표면분석의 최적조건 구하기 전략을 활용하여 구현한다.

2절에서는 2수준 속성수 f 와 3수준 속성수 g 를 변화시키면서 주효과와 모든 이인자 교호작용효과가 추정 가능한 또는 추정 불가능한 이인자 교호작용효과의 개수를 최소로 하는 블록화 혼합설계를 구현하여 응답자가 응답해야할 최소 설문 문항수를 조사하고, 마찬가지로 속성들을 모두 2수준 또는 모두 3수준 속성으로 표현한 경우 블록화 요인설계를 구현하는 최소한의 설문 문항수를 조사한다. 3절에서는 2수준 속성이 1개이고, 3수준 속성이 3개인 경우에 속성들 간의 시너지 효과가 있는 모형을 가정하고, 시뮬레이션을 통해서 생성된 선호도 설문지 자료에 대해서 설문지 문항 자료 분석 방법과 컨셉 최적화를 예시한다.

2. 문항 설계

속성들의 수준수가 2와 3인 2^f × 3^g 혼합설계는 2^f 실험설계와 3^g 실험설계의 교적설계이다. 블록화가 있는 2^f × 3^g 혼합설계의 문항설계를 생각해보자. 혼합설계의 블록의 실험점들은 2수준 속성의 각 블록에 배치된 실험점과 3수준 속성의 각 블록에 배치된 실험점들을 결합하여 구성된다. 즉 블록화가 있는 혼합설계는 2수준 블록의 실험설계와 3수준 블록의 실험설계의 교적설계이다. 예를 들어, 2수준 속성과 3수준 속성의 수가 4이고, 2수준 속성을 X₁, X₂, X₃, X₄로 표시하고 3수준 속성을 Z₁, Z₂, Z₃, Z₄로 표시한 경우 모든 주효과와 이인자 교호작용효과를 추정 가능하게 하는 블록화 혼합설계를 하기 위해 <Table 1>과 같이 2수준 블록생성인자가 b1 = X₁X₂X₃X₄인 2⁴ 실험을 2¹ 블록으로 나누어 블록화 2수준 실험설계를 생성하고, 3수준 속성은 2개의 블록생성인자 b2 = Z₂Z₃Z₄, b3=Z1Z32Z4 를 갖는 3⁴ 실험을 3² 블록으로 나누어 3수준 블록화 실험설계를 생성한다. 혼합설계의 블록은 2수준 속성들의 2¹ 개의 블록과 3수준 속성들의 3² 개의 블록들의 모든 가능한 결합으로 구성되어, 블록의 수는 2¹ × 3² = 18 개이고, 주어진 블록에서의 실험설계는 2⁴⁻¹ 실험점으로 구성된 대응되는 2수준 블록의 실험설계와 3⁴⁻² 실험점으로 구성된 대응되는 3수준 블록의 실험설계의 교적설계로 각 블록의 실험점의 수는 2⁴⁻¹ × 3⁴⁻² = 72개가 된다.

Table 1.

2 and 3 level Balanced Incomplete Block Factorial Design for 24×34

18개의 블록을 갖는 2⁴ × 3⁴ 혼합설계의 실험점들은 다음과 같이 SAS의 proc factex를 사용하여 생성될 수 있다.

이러한 방식을 일반적으로 적용하기 위해 각 수준별로 가장 최소한의 블록크기를 갖도록 하는 블록화 완전요인설계 또는 블록화 일부요인설계를 생성해야한다. 이는 임용빈(2015)에서 R 프로그램으로 생성하였으나, 본 논문에서는 SAS의 proc factex로 생성한다.

2.1. 모든 이인자 교호작용효과를 추정하는 실험점 설계

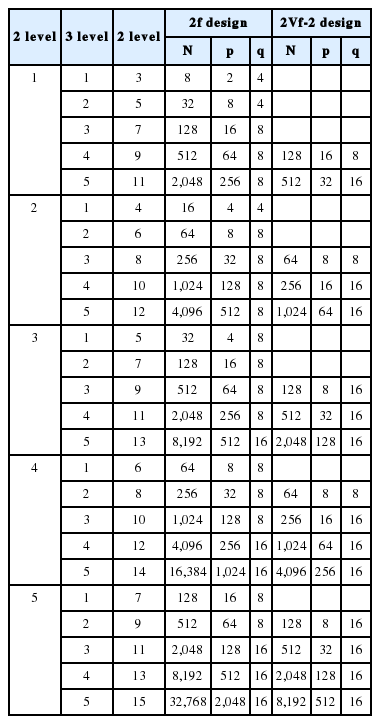
<Table 2>와 <Table 3>에 2수준과 3수준에 대한 블록화 완전요인설계 또는 블록화 일부요인설계를 생성할 수 있는 블록생성인자 및 정의대비를 나열한다. 모든 주효과 및 이인자 교호작용효과를 추정가능토록 하는 설계에 대한 정의는 <Table 2>와 <Table 3>에서 방법 열의 “model”에 해당한다. 이는 앞 절의 SAS프로그램과 같이 proc fac-tex에서 model에 추정하고자 하는 모든 효과들을 명시한 상태에서 설계된 것이다. 즉, model에 모든 주효과와 모든 이인자 교호작용효과를 명시하여 실험점을 생성한 결과이다. 이때 블록화 완전요인설계는 각 수준의 속성수가 3부터 가능하며 임의로 5개까지 제한하여 실험점을 설계한다. 블록화 일부요인설계는 각 수준의 속성수가 5부터 가능하며 2수준은 2Vf-1, 3수준은 3Vg-1 에 대한 실험을 설계한다. 이를 바탕으로 <Table 4>에서는 2수준과 3수준의 속성수 f, g 가 1부터 5 사이의 값인 경우에 모든 이인자 교호작용효과를 추정할 수 있는 블록화 혼합설계의 블록수와 블록크기 즉, 응답자수와 문항수를 살펴볼 수 있다. 앞절에서 예를 든 18개의 블록을 갖는 2⁴ × 3⁴ 블록화 혼합설계인 경우는 <Table 2.(1)>과 <Table 3.(1)>의 속성수 4개의 model 방법이 결합된 것으로 각각의 블록생성인자는 <Table 1>과 동일하고, 그때의 블록개수와 블록크기는 2 × 9 = 18 개의 블록개수(응답자수)에 8 × 9 = 72 개의 블록크기를(문항수) 갖게 되어 <Table 4.(1)>에서 2수준 속성수 4개인 행과 3수준 속성수 4개인 열이 만나는 칸의 값인 72(18) 이다. 이와 같이, 모든 이인자 교호작용효과를 추정하는 실험설계인 경우에는 <Table 4.(1)>과 같이 2수준 속성수가 4개 이상 이고 3수준 속성수가 2개 이상이면 응답자가 응답해야할 설문 문항수가 70개가 넘어 응답자로부터 정확한 답변을 기대하기가 어렵게 된다. 이러한 경우, 블록 당 문항수를 줄이기 위해서는 블록의 수를 많게 해야 하기에 불가피하게 블록과 교락될 일부 이인자 교호작용효과를 허용해야 하고, 이 교호작용효과는 추정이 불가능하게 된다. 이 경우에 이인자 교호작용효과 중 일부의 추정 불가능을 허용하되 그것의 개수를 최소로 하는 블록화 혼합설계 방법을 다음과 같이 제안한다.

Table 2.

2 level Balanced Incomplete Block Factorial Design (N: number of runs, p: number of blocks, q: block size)

Table 3.

3 level Balanced Incomplete Block Factorial Design (N: number of runs, p: number of blocks, q: block size)

Table 4.

Block size and number of blocks for 2f×3g mixed factorial design (p: number of blocks, q: block size)

2.3. 모두 2수준으로 변경할 경우

2와 3수준의 혼합설계일 경우 3수준 속성을 2수준 속성 2개로 표현하여 2수준 블록화 요인설계를 활용하여 설계하는 방법을 제안한다. 일반적으로 <Table 5>와 같이 3수준 Z₁를 2수준 속성 X₁, X₂로 변경할 수 있다. Z₁ = 1은 X₁ = X₂ = 1, Z₁ = 2은 X₁과 X₂가 서로 다른 수준일 경우 그리고 Z₁ = 3은 X₁ = X₂ = 2 인 경우로 정의할 수 있다. 혼합설계와 비교하면 모두 2수준으로 변경한 경우 속성의 수는 증가하나, <Table 6>과 같이 모든 이인자 교호작용효과가 추정가능하면서도 블록 크기가 줄어들어 설문지 문항수를 줄일 수 있는 효과가 발생된다. 이때, SAS의 proc factex에서 model 옵션에 추정해야 할 요인들을 나열하여 실험점을 찾는데, 3수준 속성을 2수준 속성 속성 2개로 정의한 2개 속성들 사이의 교호작용효과는 추정하지 않아도 되어 임용빈 (2015) 또는 <Table 2>의 실험설계와는 다를 수 있다. 또한, 2수준 블록화 완전요인설계는 총 실험수가 많아져 응답자의 수가 많아지게 됨으로 총 실험수를 줄여 응답자수도 줄일 수 있는 2Vf-2 블록화 일부요인설계도 제안하고자 한다. <Table 6>을 보면 최소 블록크기 즉 설문지 문항수는 최소 8개에서 16개 까지 가능하다.

Table 5.

Make 2 level factors from a 3 level factor

Table 6.

2 level Balanced Incomplete Block Factorial Design (N: number of runs, p: number of blocks, q: block size)

2.4. 모두 3수준으로 변경할 경우

2와 3수준의 혼합설계에서 더미 수준 기법을 활용하여 2수준 속성을 3수준 속성으로 표현하여 3수준 블록화 요인설계를 활용하는 방법을 제안한다. 즉, 모두 3수준인 것처럼 실험을 설계하되, 원래 2수준에 대응되는 3수준 속성의 수준 (1,2,3)를 (1,2,2)로 변경하여 각 속성의 수준 결합에 따라서 설문 문항을 작성한다. 속성수는 혼합설계와 동일하고 모든 이인자 교호작용효과까지 추정가능토록 하는 블록화 완전요인설계를 할 수 있다. <Table 7>과 같이 응답자별 설문 문항수는 최소 9개에서 27개이며, 응답자의 수를 줄이기 위해 3Vg-2 블록화 일부요인설계를 고려할 수도 있다.

Table 7.

3 level Balanced Incomplete Block Factorial Design (N: number of runs, p: number of blocks, q: block size)

3. 설문지 문항 자료 사례 분석

2수준 속성이 1개이고, 3수준 속성이 3개인 2¹ × 3³인 경우에 대하여 시뮬레이션 모형으로 생성한 데이터를 분석한다. 2절에서 소개한 혼합설계 및 수준수를 통일하는 방법 등을 고려하여 블록화 요인설계를 하여도 정밀한 데이터 분석 결과를 얻을 수 있는지 살펴보고자 한다.

설계단계에서 모든 이인자 교호작용효과까지 추정이 가능토록 하는 블록화 요인설계를 하며, 일반적인 블록화 완전혼합설계를 하면 <Table 8>과 같이 최소한의 응답자별 문항수가 18개로 응답하기에 적당한 수준이 된다. 또한, 이보다 더 문항수를 줄일 수 있는 설계로는 모두 2수준으로 변경하여 블록화 일부요인설계를 하면 8문항이 되고, 모두 3수준으로 변경하여 블록화 완전요인설계를 하면 9문항이 된다. 설문 응답자는 각각의 문항에 대해 각자의 선호에 따라 9점 척도로 선호도 점수를 매기고 모든 설문지를 합쳐 분석하면 모든 주효과와 이인자 교호작용효과를 독립적으로 추정가능하다.

Table 8.

Designs used in the simulation study (N: number of runs, p: number of blocks, q: block size)

2수준 속성 X₁과 3수준 속성 Z₁, Z₂, Z₃의 혼합설계를 이용하여 문항 설계를 한다면, 설문 응답자는 18개 각각의 문항에 대하여 1점에서 9점까지 선호도 점수를 매긴다. 각각의 문항에 대한 응답자들의 선호도 점수를 시뮬레이션 모형에 의해 생성하기 위해 주효과 X₁, Z₁, Z₂와 이인자 교호작용효과 X₁Z₁를 이용한 효용함수를 가정한다. 주어진 문항에 대한 선호도 점수는 <Equation (1)>과 <Table 9>에 주어진 가정된 효과의 크기에 따라서 생성된 후에, 1점에서 9점까지 최종 선호도 점수는 <Equation (1)>로부터 생성된 모든 y값의 분포에 따라 등간격으로 나눈 후 부여한다.

Table 9.

Size of effects in the simulation model

위 가정에 따르면 평균 선호도 점수를 최대로 하는 이론적인 컨셉 최적조건은 X₁₍₁₎Z₁₍₃₎Z₂₍₃₎ 이다. 혼합설계 및 모두 2수준이나 3수준으로 변경하여 설계한 후 분석하여도 최적조건을 올바르게 찾아줄 수 있는지 비교해 보고자 한다.

3.1. 혼합설계일 경우: 블록화 2¹ × 3³ 완전혼합설계

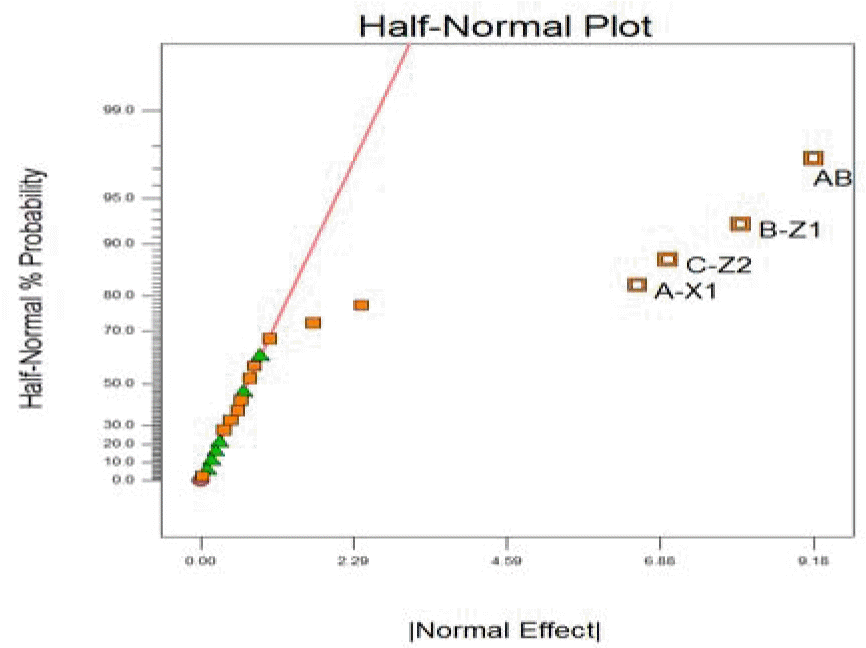
<Table 8>과 같이 3수준에 대한 블록생성인자 b1 = Z₁Z₂Z₃로 블록화 완전요인설계를 한 후 2수준과 결합하면 응답자 3명 각각에 서로 다른 18개의 설문 문항을 설계할 수 있다. 이를 모두 합쳐 분석하면 블록화 완전요인설계 실험자료의 분석과 동일해 지며, 주효과 및 이인자 교호작용효과까지 모두 추정가능하다. <Figure 1>은 Design Expert 10의 반정규 확률그림으로 주효과 X₁, Z₁, Z₂와 이인자 교호작용효과 X₁Z₁를 유의한 효과로 선택할 수 있다. 이는 <Equation (1)>에서 가정한 유의한 효과들과 일치한다.

Figure 1.

Half normal probability plot(Design Expert 10)

선별된 X₁, Z₁, Z₂, X₁Z₁ 효과에 대한 추정치로 주효과 X₁, Z₁, Z₂ 속성들의 수준 결합에 대해서 평균 선호도의 추정치인 ŷ 를 최대로 하는 컨셉 최적조건을 찾으면 X₁₍₁₎Z₁₍₃₎Z₂₍₃₎이고, 이때의 ŷ = 8.5가 된다. 이는 이론적인 컨셉 최적조건과 일치한 결과이다.

3.2. 모두 2수준일 경우: 블록화 2V7-1 일부요인설계

3수준 속성을 2수준 속성 2개로 표현하여 3수준 3개의 속성은 2수준 6개의 속성으로 대체된다. 6개의 2수준 속성을 X₂부터 X₇로 표시할 때에, 3수준 속성인 Z₁은 X₂와 X₃, Z₂는 X₄와 X₅ 그리고 Z₃는 X₆과 X₇으로 표현된다. 주효과 및 모든 이인자 교호작용효과가 추정 가능해야하나, 동일한 3수준 속성을 표현하는 2수준 속성들 간의 교호작용효과인 X₂X₃, X₄X₅, X₆X₇ 교호작용효과 추정은 관심이 없기에 제외하도록 한다. 최소한의 응답자 수가 되도록 블록화 일부요인설계를 하면, <Table 8>과 같이 8명의 응답자가 8개의 설문 문항에 답하면 된다. 혼합설계에 비해 응답자수는 증가하였으나, 설문 문항수는 줄었다.

소비자 선호도를 시뮬레이션 모형으로 생성하기 위해 가정한 효과의 크기는 <Table 9>와 동일하며 이를 2수준 속성을 이용해서 표현하면 <Equation (2)>와 같이 정의할 수 있다. 예를 들어, z₁₍₁₎ = −1.5은 2수준으로 표현하면 X₂, X₃의 수준값이 모두 1 일 때, z₁₍₃₎ = 1.5은 X₂, X₃가 모두 2 일 때 그리고 z₁₍₂₎ = 0은 X₂와 X₃의 수준값이 서로 다를 때이다.

(2)z1(j)={−1.5,when X2=X3=10,X2≠X31.5,X2=X3=2z2(k)={−1,when X4=X5=10,X4≠X51,X4=X5=2x1(1)z1(j)={−1.5,when X2=X3=10,X2≠X31.5,X2=X3=2x1(2)z1(j)={−1.5,when X2=X3=10,X2≠X3−1.5,X2=X3=2

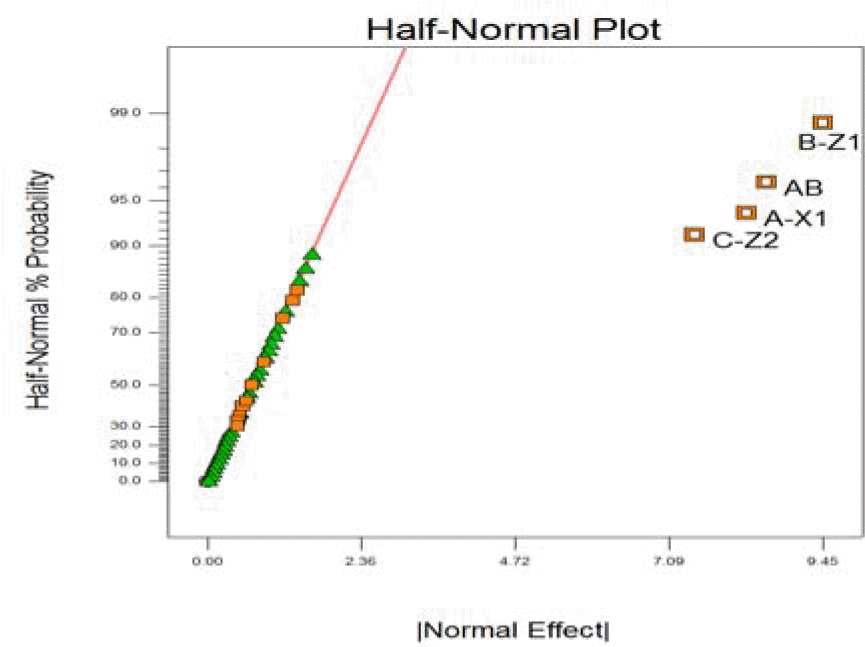
평균 선호도 점수를 최대로 하는 이론적인 컨셉 최적조건은 X₁₍₁₎X₂₍₂₎X₃₍₂₎X₄₍₂₎X₅₍₂₎이고, 이는 혼합설계 속성으로 표현하면 X₁₍₁₎Z₁₍₃₎Z₂₍₃₎가 된다. <Figure 2>의 Design Expert 10의 반정규 확률그림을 통해 주효과 X₁, X₂, X₃, X₄, X₅와 이인자 교호작용효과 X₁X₂, X₁X₃가 유의한 효과로 선택될 수 있고, 이는 혼합설계 속성에서 X₁, Z₁, Z₂, X₁Z₁가 유의하게 선택 되어진 것과 동일한 것이다. (참고로, <Figure 2>에서 X₄ 아래에 있는 속성은 X₂X₃X₇ 삼인자 교호작용으로 효과 추정의 대상이 아니다.)

Figure 2.

Half normal probability plot(Design Expert 10)

선별된 속성 X₁, X₂, X₃, X₄, X₅ 들의 모든 가능한 수준 결합에 대해서 선별된 효과를 추정치로 대체하여 얻어진 평균 선호도의 추정치인 ŷ를 최대로 하는 컨셉 최적조건은 X₁₍₁₎X₂₍₂₎X₃₍₂₎X₄₍₂₎X₅₍₂₎이고, 이는 혼합설계의 X₁₍₁₎Z₁₍₃₎Z₂₍₃₎으로 이론적인 컨셉 최적조건과 일치한 결과이다.

3.3. 모두 3수준일 경우: 블록화 3⁴ 완전요인설계

2수준 속성 X₁을 3수준 속성으로 표현하여 속성들이 모두 3수준인 블록화 3⁴ 완전요인설계를 한다. 4개 속성의 주효과 및 모든 이인자 교호작용효과가 추정 가능한 블록화 완전요인설계를 하면 <Table 8>과 같이 9명의 응답자에 9개의 설문 문항을 설계할 수 있다. 혼합설계에 비해서는 설문 문항이 절반 정도 감소하였으나, 모두 2수준으로 변경하였을 때 보다는 응답자 수 1명 증가, 설문 문항도 1문항 증가하였다. 실험점 생성 후, 속성 X₁에 대해서는 대응되는 속성의 3수준인 (1,2,3)를 (1,2,2)로 변경하여 설문 문항을 만들고 소비자 선호도를 시뮬레이션 모형으로 생성하기 위해 가정한 효과의 크기는 <Table 9>와 동일하다. 물론, 평균 선호도 점수를 최대로 하는 이론적인 컨셉 최적조건도 X₁₍₁₎Z₁₍₃₎Z₂₍₃₎가 된다. <Figure 3>과 같이 Design Expert 10의 반정규 확률그림에서 선택된 유의한 효과는 주효과 X₁, Z₁, Z₂와 이인자 교호작용효과 X₁Z₁이다. 이는 <Equation (1)>에서 가정한 유의한 효과들과 일치한다.

Figure 3.

Half normal probability plot(Design Expert 10)

선별된 속성들인 X₁, Z₁, Z₂ 의 모든 가능한 수준 결합에서 평균 선호도의 추정치인 ŷ를 최대로 하는 컨셉 최적조건은 이론적인 것과 일치한 X₁₍₁₎Z₁₍₃₎Z₂₍₃₎가 된다.

4. 결 론

이 논문에서는 컨조인트 분석의 컨셉을 구성하는 속성들의 수준수가 동일하지 않고 2와 3수준으로 혼합되어 있는 경우 2수준 속성수 f 와 3수준 속성수 g 를 변화시키면서 주효과와 모든 이인자 교호작용효과가 추정 가능한 또는 추정 불가능한 이인자 교호작용효과의 개수를 최소로 하는 블록화 혼합설계를 구현하여 설문지 문항설계를 제시하고, 응답자가 응답해야할 최소 설문 문항수를 조사한다. 또한 3수준 속성을 2개의 2수준 속성으로 표현하거나 2수준 속성을 더미 수준법을 활용하여 3수준 속성으로 표현하여서, 속성들을 모두 2수준 또는 모두 3수준 속성으로 표현한 경우 블록화 요인설계 혹은 블록화 일부요인설계를 구현하는 최소한의 설문 문항수를 조사한다. 문항설계 단계에서 제안된 3가지 방법 중에서 어느 방법을 적용할 지는 <Table 4>, <Table 6>, <Table 7>에 주어진 각 방법의 응답자수와 문항수를 검토하고 실용성을 고려하여 결정한다. 사례분석으로 2수준 속성이 1개이고, 3수준 속성이 3개인 경우에 속성들 간의 시너지 효과가 있는 모형을 가정한다. 시뮬레이션을 통해서 생성된 선호도 설문지 자료에 대한 사례 분석한 결과를 보면, 제시한 방법들이 가정한 유의한 효과들을 효율적으로 검출하고 이론적인 컨셉 최적조건들을 잘 찾고 있다.

Article information Continued