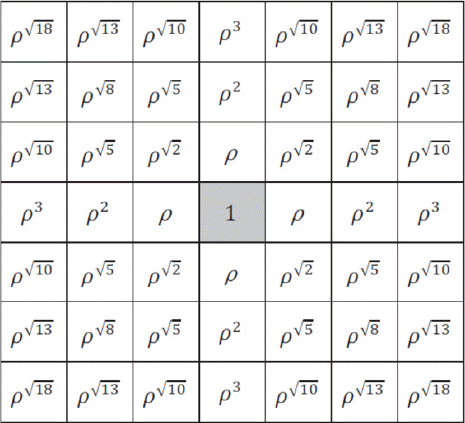시공간 탐지 정확성을 고려한 다변량 누적합 관리도의 비교
Comparison of Multivariate CUSUM Charts Based on Identification Accuracy for Spatio-temporal Surveillance
Article information
Abstract
Purpose:
The purpose of this study is to compare two multivariate cumulative sum (MCUSUM) charts designed for spatio-temporal surveillance in terms of not only temporal detection performance but also spatial detection performance.
Method:
Experiments under various configurations are designed and performed to test two CUSUM charts, namely SMCUSUM and RMCUSUM. In addition to average run length(ARL), two measures of spatial identification accuracy are reported and compared.
Results:
The RMCUSUM chart provides higher level of spatial identification accuracy while two charts show comparable performance in terms of ARL.
Conclusion:
The RMCUSUM chart has more flexibility, robustness, and spatial identification accuracy when compared to those of the SMCUSUM chart. We recommend to use the RMCUSUM chart if control limit calibration is not an urgent task.
1. 서 론
전통적 품질관리에서 관리도는 어떠한 프로세스가 통계적으로 제어된 상태에 있는지 아닌지를 감시하는 데에 쓰여 왔다. 일반적으로 관리도는 매 시간 단위마다 주어진 정보를 바탕으로 통계량을 계산하고, 그 계산된 통계량이 정해진 관리한계를 넘어서면 그에 해당하는 프로세스가 잠재적 통제 불능 상태에 빠졌을 수 있다는 것을 알리는 경보를 울린다. 이러한 관리도의 주목적은 통제 불능 상태로 변한 프로세스를 빨리 감지해 내는 것에 있으며, 관리도의 성능 평가는 ARL0와 ARL1을 기반으로 이루어져왔다. ARL0는 프로세스가 정상 통제 상태 아래에 있을 때 오경보를 울릴 때 까지 걸리는 평균 정보 추출 횟수(즉, 오경보를 울릴 때까지 소요되는 평균 단위 시간)를 대표하며, ARL1은 프로세스가 실제로 통제 불능 상태에 있을 때 경보를 울리는 데까지 걸리는 평균 정보 추출 횟수(즉, 경보를 울릴 때까지 소요되는 평균 단위 시간)를 대표한다(Montgomery 2009). 일반적으로 관리도는 정해진 특정 ARL0를 달성할 수 있도록 관리한계를 미리 설정하고, 그 관리한계를 적용하였을 때 더 작은 ARL1을 달성할수록 더 좋은 탐지 성능을 가진 것으로 간주된다.
시공간 감시를 위한 관리도는 하나의 프로세스를 관측하고 감시하는 것만이 아니라 여러 지역의 프로세스를 동시에 관측하고 감시하는 것을 가능하게 하는 관리도로, 제조 공정에서의 이미지 분석을 이용한 불량 탐지, 역학에서의 질병 전파 범위 탐지 등의 용도로 사용되어 왔다 (He et al. 2014, Lee et al. 2014, 2015). Lawson (2007), Sonesson and Bock(2003), Tsui et al. (2008), 그리고 Woodall (2006)은 역학을 위한 다양한 통계적 시공간 감시 방법론들을 소개하고 그를 비교분석하였다. (여기에서 언급된 대부분의 방법론은 기초가 되는 자료가 정규분포, 혹은 포아송 분포를 따른다고 가정하고 있다.) Fricker et al. (2008)은 한 가지 누적합 관리도, 두 가지 종류의 슈하트 관리도, 그리고 한 가지 가중이동평균 관리도를 선택하여 여러 환경에서 시험한 후 누적합 관리도가 다른 관리도에 비해 더 뛰어나다고 평가하였으며, Han et al. (2010) 역시 누적합 관리도와 지수가중이동평균 관리도, 검색 통계량을 이용한 관리도의 ARL1 성능을 비교하고 누적합 관리도와 지수가중평균 관리도가 검색 통계량을 이용한 관리도보다 그 탐지 성능이 뛰어나다고 발표하였다. 이렇게, 누적합 관리도는 프로세스의 작은 변화에도 민감하게 반응하여 프로세스의 상태변화를 빠르게 알아차릴 수 있어 많은 학자들에 의해 연구되어 왔으며, 특히 자료에 지역적 상관관계가 강하게 존재하는 경우에는 여러 개의 단변량 누적합 관리도를 운영하는 것보다 하나의 다변량 누적합(MCUSUM) 관리도를 운영하는 것이 ARL1 면에서 더 뛰어난 성과를 보인다고 알려져있다(Woodall and Ncube 1985, Rogerson and Yamada 2004).
Jiang et al. (2011)은 지역적 상관관계를 고려한 시공간 탐지 방법론으로써 원형의 지역 군집을 감시 대상으로 하는 새로운 다변량 누적합 관리도를 제안하였다. 이 관리도는 관측되는 자료가 다변량 정규분포를 따른다고 가정하고 목표로 하는 ARL0을 달성할 수 있는 관리한계를 찾아내기 위해 시뮬레이션을 이용하는데, 환경이 자주 바뀌거나 관측 대상 지역의 수가 매우 많은 경우에는 이 시뮬레이션에 오랜 시간과 노력이 소모된다. 이러한 단점을 극복하기 위해 Lee et al. (2014)는 Jiang et al. (2011)이 제안한 통계량을 통계적 성질에 따라 여러 개로 나누고 나뉘어진 통계량 각각에 시뮬레이션 대신 간단한 수치적 계산을 통해 얻어진 관리한계를 부여하는 Separated-MCUSUM (SMCUSUM) 관리도를 개발하였고, 이 SMCUSUM 관리도는 일정 범위 안에서 Jiang et al. (2011)과 근사한 시간적 탐지 성과를 보이는 것으로 알려져 있다. SMCUSUM 관리도는 간편한 관리한계 추정 식을 제공하지만, 자료가 다변량 정규분포를 따르거나 다변량 정규분포로 근사할 수 있는 분포를 따를 때에만 사용이 가능하다. 따라서 Lee et al. (2015)은 자료의 기저 분포가 명확히 알려져 있지 않은 경우에도 안정적으로 사용할 수 있는 Robust-MCUSUM (RMCUSUM) 관리도를 개발하였다.
여기서 한 가지 주목해야 할 점은 현재까지 발표된 많은 관련 논문 안에서 시공간 감시를 위해 설계된 관리도의 성능이 주로 ARL1면에서만 보고되고 평가되어 왔다는 것이다. 하지만 시간과 공간을 모두 감시하기 위한 관리도에서 단순히 시간적 탐지 성과(즉, 얼마나 빨리 프로세스의 변화를 찾아내는지)만을 기반으로 어떠한 관리도가 다른 관리도보다 더 뛰어나거나 부족하다고 평가하는 것은 충분치 않은 일이며, 따라서 시간적 탐지 성과뿐만이 아닌 공간적 탐지 성과(즉, 변화가 일어난 지역을 얼마나 정확히 찾아내는지)에 대한 평가도 반드시 함께 이루어져야할 것이다.
SMCUSUM 관리도와 RMCUSUM 관리도는 둘 모두 시공간 감시를 목적으로 하는 다변량 누적합 관리도이면서 (사용 가능한 환경 조건은 다르지만) 같은 환경 아래에서는 비슷하게 뛰어난 ARL1 성과를 내는 것으로 알려져 있다. 허나 본 연구에서는 시간적 탐지 성과뿐만이 아닌 공간적 탐지 성과를 추가로 고려하여 두 관리도를 다각도로 비교 분석하고, 시간적 탐지 성과만을 비교하여 관리도를 평가하는 것이 과연 타당한 일인가에 대해 보다 심도있게 고찰하고자 한다.
2. 연구 배경
본 장에서는 각각 SMCUSUM과 RMCUSUM으로 이름 붙여진 두 가지 다변량 누적합 관리도를 소개한다. 본래 전염성이 강한 질병의 전파, 해충 번식에 의한 농작물 피해 등 하나의 오염원의 발생에 따른 주변의 피해를 탐지하기 위한 목적으로 설계된 두 관리도를 본격적으로 소개하기에 앞서, 먼저 두 관리도 모두에 적용되는 배경 문제와 가정, 공통적으로 쓰이는 기호에 대해 간략히 설명한다 (Lee et al. 2014, 2015).
관측 대상이 되는 총 공간 영역은 사각형 모양의p = M × N 개 지역으로 가정한다. 각 지역 c에서는 매 정해진 시각 t에 관측치 자료가 생성되며, 이 자료는 각 지역의 프로세스가 정상적으로 통제되고 있다는 가정 아래 표준화되어 xt = (xt1, xt2, …, xtp)‘ 라는 벡터로써 보고된다. 즉, x15 는 첫 번째 단위 시각에 5번 지역에서 생성된 자료가 표준화된 값을 이른다. xt 는 평균 벡터 μ 와 분산-공분산 행렬 Σ를 가지는 어떠한 확률 밀도 함수를 따르며, 이때 이 Σ는 시간이나 통제 상태에 영향 받지 않는다고 가정한다. xt가 표준화된 자료에 기인하고 있기에, 정상 통제 상태 하에서의. μ는 0 벡터와 같다. 알려지지 않은 어떤 시점 ν에 어떤 지역의 프로세스가 통제 불능 상태가 되면, 평균 벡터. μ는 0 벡터가 아닌 다른 어떤 벡터로 바뀌게 되고, SMCUSUM과 RMCUSUM 관리도는 둘 모두 이러한 평균 벡터의 변화를 가능한 빨리 그리고 정확히 찾아내는 것을 목표로 한다.
원칙상으로는 관측 대상이 되는 p개의 지역 중 통제 불능 상태에 빠지는 지역의 위치, 개수 및 형태에 아무런 제약도 존재하지 않으나, 본 연구에서 고려하는 두 관리도는 Jiang et al. (2011)의 연구를 바탕으로 편의상 오염원으로 인한 피해가 원형의 군집 형태로 일어날 것임을 가정한다. 이 원형의 군집은 중심지역 c와 반지름 r에 의해 정의되는데, 군집 Oc, r 은 중심지역 c로부터 유클리디언 거리 기준으로 r이하만큼 떨어져 있는 모든 지역을 원소로 포함하는 집합을 뜻한다. <Figure 1>은 p=7×7=49개 지역 고려 시 각 지역을 2차원 평면상의 좌표로 표현한 것으로, 이 좌표에 따르면 지역 25와 지역 32 사이의 유클리디언 거리는 1, 지역 25와 지역 33 사이의 거리는
7×7 Regions ― Region c and Its 2-dimensional Coordinate.
피해의 범위와 군집의 크기는 r로 대변될 수 있다. 피해 범위의 예상이 가능한 경우에 r은 하나의 값으로 고정될 수 있고, 정확한 피해 범위를 모른 채 여러 가지 크기의 군집을 모두 감시하여야 하는 경우에 r은 다양한 값을 가질 수 있도록 설정될 수 있다. 이 r이 가질 수 있는 값들의 집합은 R로 정의하며, <Figure 1>의 예에서 R = {0}인 경우에 감시해야할 대상 군집의 개수는 49개, R = {0, 1}인 경우에 감시해야할 군집의 개수는 49×2=98개로, R에 포함된 값의 개수가 늘어날수록 감시 대상이 되는 군집의 개수 또한 늘어나게 된다.
특정 군집 Oc, r 에 피해가 발생하여 통제 불능 상태가 된다는 것은 군집 외 지역은 정상인 상태에서 군집에 포함된 지역의 자료 평균이 일정하게 크기 δ > 0 만큼씩 증가하는 것으로 가정한다. 이때 변화된 평균 벡터를 μc, r로 정의하며 이 때μc, r 의 j번째 원소는 j ∈Oc, r인 경우에는 δ, 그 외의 경우에는 0이 된다. 지역 간의 상관관계는 지역 간의 유클리디언 거리와 역의 관계가 있으며 이는 ρ라는 모수를 이용하여 표현된다고 가정한다. 따라서 군집들 사이에도 일정 상관관계가 존재할 수 있다.
2.1 SMCUSUM 관리도
SMCUSUM 관리도의 기본이 되는 관찰 통계량은 아래와 같다.
이는 Jiang et al. (2011)이 제안한 통계량에 기반한 것으로
Lee et al. (2014)은 SMCUSUM 관리도의 xt가 다변량 정규분포를 따른다는 가정 하에 목표로 하는 ARL0값을 얻을 수 있도록 하는 h*r 를 곧바로 추정할 수 있는 식을 제공하고 있다. 본페로니 조정을 기반으로 하는 이 추정방식은 p, ρ, δ, r 값이 어떻게 설정되느냐에 따라 그 정확도가 조금씩 달라지는데, 보통
Jiang et al. (2011)이 개발한 관리도를 포함한 다른 관리도들이 일반적으로 무수한 시뮬레이션을 통한 시행착오를 거쳐 관리한계 값을 설정하는 것에 비해 SMCUSUM 관리도는 훨씬 빠르고 간편하게 관리한계를 설정 할 수 있어 질병의 전파와 같이 기존 자료가 부족하고 환경이 빠르게 변화하여 관리도의 신속한 설정이 중요시 되는 상황에서 큰 효과를 발휘할 수 있다.
2.2 RMCUSUM 관리도
SMCUSUM 관리도는 간편한 관리한계 추정 식을 제공하지만, κ가 2 이상이 되면 관리한계 추정 오차가 커져 그 쓰임에 제한을 받는다. 또한, SMCUSUM 관리도는 xt 가 다변량 정규분포를 따른다는 가정 아래 설계되어 자료의 분포가 다변량 정규분포를 따르지 않는 경우에는 사용이 어렵다. 따라서 지역간 상관관계가 크거나, 피해 범위 예상이 어려운 경우, 자료의 분포가 알려져 있지 않은 경우 등에서 관리도를 더욱 유연하고 안정적으로 쓸 수 있도록 하기 위해 Lee et al. (2015)은 다음을 기본 관찰 통계량으로 하는 RMCUSUM 관리도를 개발하였다.
여기서 κ는 관리도의 운영 특성을 조정하는 기준 상수로, 자료가 정규분포를 따를 때에는 0.5, 포아송 분포를 따를 때에는 0.1의 값이 추천된다(Kim et al., 2007). (만약 이κ가
RMCUSUM 관리도에서도 r의 크기에 따라
RMCUSUM 관리도는 함수적 중심 극한 정리가 성립한다는 가정 아래, 자료 분포에 상관없이 목표로 하는 ARL0값을 얻을 수 있도록 하는 관리한계 g*r 을 추정한다. (
3. 실험 및 결과 분석
지금껏 SMCUSUM 관리도와 RMCUSUM 관리도를 포함한 많은 시공간 탐지를 위한 관리도들은 얼마나 빨리 통제 불능 상태에 빠진 군집을 탐지해낼 수 있는지에 대해서만 집중 비교되어 왔다. 그 시간적 성과 기준으로는 ARL1이 사용되어 왔고 이 기준에 따르면, RMCUSUM 관리도는 (그 범용성에 대한 이점을 제외하면) ARL 성과 면에 있어서는 SMCUSUM 관리도와 크게 차이가 나지 않을 것으로 기대된다(Lee et al., 2015). 허나, 이렇게 이상 상태가 탐지 될 때까지의 시간을 근거로 하는 기준은 시간과 공간을 모두 탐지 해낼 목적으로 설계된 관리도의 성과 비교 기준으로 충분하다고 할 수 없으므로, 본 연구에서는 SMCUSUM과 RMCUSUM 관리도를 다각도로 실험하고, 그 시간적 탐지 신속성뿐만 아니라 공간적 탐지 정확성을 종합적으로 비교하고 분석한다.
3.1 실험 배경
SMCUSUM과 RMCUSUM관리도의 비교를 위해 우리는 <Figure 1>과 같은 ρ =7×7=49 개의 지역을 관찰 대상 지역으로 가정한다. 어느 실험에서든 목표로 하는 ARL0 값은 100으로 설정하고, 이에 따른 관리 한계를 각 관리도에 맞는 방법으로 도출한다. 한 지역이 통제 불능 상태에 빠지면 해당지역의 표준화된 자료의 평균은 δ=1 만큼 증가하는 것으로 한다. 즉, (자료를 표준화하기 전 기준으로) 한 지역이 통제 불능 상태가 된다는 것은 해당 지역의 자료의 평균이 그 지역의 표준편차만큼 증가하는 것을 의미한다.
각 지역의 자료 사이에는 상관관계가 있을 수 있으며, 이 상관 관계는 두 지역 간의 거리가 멀수록 약화될 것으로 가정한다(Lee et al. 2014, 2015). 2장에서도 언급하였듯 이 상관관계는 p라는 모수를 통해 표현되는데, 본 실험에서는 49개 지역 중 임의의 두 지역 a와 b 사이의 상관계수를ρDist(a, b) 로 설정하며, 여기에서 Dist(a, b) 는 a 지역과 b 지역간의 유클리디언 거리를 말한다. 하나의 예로써 <Figure 2>는 지역 25와 다른 대상 지역사이의 상관계수 설정을 보여주고, <Figure 3>은 설정된 ρ값과 거리에 따라 두 지역 간의 상관관계가 어떻게 변화하는지 보여준다. 이러한 상관계수 설정에 따라 Σ는 자연스럽게 구성될 수 있다.
Correlation Settings for Region 25.
Correlation Structure.
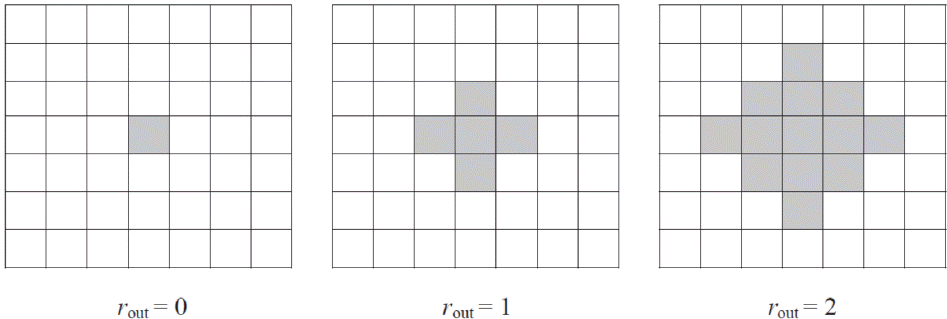
ARL1 측정을 위해서는 통제 불능 상태의 군집이 존재하여야 하므로, 본 연구에서는 편의상 이 통제 불능 군집을 O25, rout 로 설정한다. 지역 25를 중심으로 하는 이 군집은 <Figure 4>와 같이 rout 의 설정에 따라 세 가지 형태로 나뉘어 실험에 이용된다. r이 관리도에서 탐지하고자 하는 통제 불능 군집의 크기를 의미한다면, rout 은 실제 통제 불능 군집의 크기를 의미한다.
Clusters in Out-of-control State.
SMCUSUM 관리도는 자료가 다변량 정규분포를 따를 때에만 적용 가능한 반면, RMCUSUM은 자료의 분포에 상관없이 적용 가능하므로, 자세한 비교를 위해 실험에서는 두 가지 기저 분포를 사용하여 원 자료를 생성한다. 하나는 평균 벡터 μ 를 가진 다변량 정규분포이고, 다른 하나는 모든 요소가 5인 평균 벡터를 가진 다변량 포아송 분포이다. 전자는 SMCUSUM과 RMCUSUM 관리도 모두를 위해 사용되고, 후자는 RMCUSUM의 평가를 위해 사용된다. RMCUSUM 관리도에서 κ는 정규분포 사용 시와 포아송 분포 사용 시에 각각 0.5와 0.1로 설정한다.
관리도의 탐지 신속성과 정확성 조사를 위해 각 환경 설정 조합 마다 실험은 10000번씩 되풀이 된다. 시간상 탐지 신속성의 측정 기준인 ARL1 외에 공간상 탐지 정확성을 측정하기 위해 우리는 두 가지 기준을 도입한다. 그 첫 번째 기준은 정합율이다. 이 정합률은 전체 10000번의 실험 중 통제 불능 상태에 빠진 원형의 군집만을 정확하게 찾아내는 비율로 정의한다. 즉, 정합률은 통제 불능 상태로 변한 지역과 정상 상태인 지역을 완벽하게 구분 짓는 비율을 말한다. 두 번째 기준은 내포율이다. 내포율은 전체 실험 중 관리도에 의해 탐지된 군집이 실제 통제 불능상태에 빠진 지역을 모두 포함하고 있는 경우의 비율로 정의된다. 즉, 실제 통제 불능상태에 빠진 군집보다 공간상 더 큰 군집에 이상이 있다고 판단하였으나, 탐지 된 큰 군집이 실제 통제 불능 상태에 빠진 군집을 온전히 포함하고 있는 경우에는 내포율 계산에 포함될 수 있다. 내포율은 언제나 정합률과 같거나 큼에 유의하라. (상태 변화가 일어나는 범위에 대한 예상이 어렵거나 통제 불능 상태로 변한 지역을 탐지 하지 못할 시 일어날 수 있는 피해 정도가 클 때에는 r의 값을 여유 있게 설정 하거나 여러 가지 r값을 동시에 사용하여 탐지하게 된다. 그러므로 이러한 상황에서는 정합률과 더불어 내표율을 살피는 것이 관리도의 탐지 정확성을 비교하는 데에 더 많은 도움을 줄 것이다.)
이 외 SMCUSUM이나 RMCUSUM 관리도를 운영하는 데에 필요한 실험 환경 변수는 Lee et al. (2015)에서의 연구와 같게 조성하였음을 밝혀둔다.
3.2 실험 결과 및 분석
SMCUSUM과 RMCUSUM 관리도 운영을 위한 관리한계의 정확성에 대한 분석은 Lee et al. (2015)의 연구에서 충분히 언급되어 있으므로, 본 장에서는 실제 달성된 ARL0 값에 대한 결과 분석은 생략하고 ARL1과 정합률, 내표율에 관한 결과만을 비교 분석한다. SMCUSUM 관리도는 자료가 다변량 정규분포를 따를 때에만 운영 가능하므로, 두 관리도의 성과 비교는 기본적으로 다변량 정규 분포를 따르는 자료를 토대로 이루어졌다.
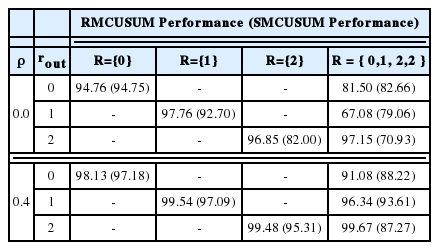
<Table 1>에서는 고려된 각 실험 환경 아래에서 SMCUSUM과 RMCUSUM 관리도의 시간적 탐지 성과를 나타내는 ARL1을 비교한다. 두 관리도 모두 자료에 지역적 상관관계가 존재하는 경우, 그리고 실제로 통제 불능 상태에 빠진 군집의 크기가 크면 클수록 더욱 신속하게 경보를 울리는 경향을 보인다. RMCUSUM 관리도는 실제 통제 불능 상태가 된 군집의 크기가 관리도에서 감시되는 군집의 크기보다 작은 (즉, rout < r인) 경우에 SMCUSUM 관리도에 비해 더 작은 ARL1 값을 가진다. 예를 들어, 자료에 지역적 상관관계가 존재하지 않을 때 rout 이 0인상태에서 r은 2만 고려되는 경우, RMCUSUM 관리도는 평균 36.40 단위시간 만에 경보를 울리지만, SMCUSUM 관리도는 평균 66.68 단위 시간이 지나서야 경보를 울린다. 그러나 그 외에 rout ≥ r인 경우나, 여러 가지 r값이 모두 함께 고려되는 경우에는 RMCUSUM 관리도의 ARL1은 SMCUSUM 관리도의 그것과 비슷하거나 더 큰 값을 가진다.
ARL1 Comparison
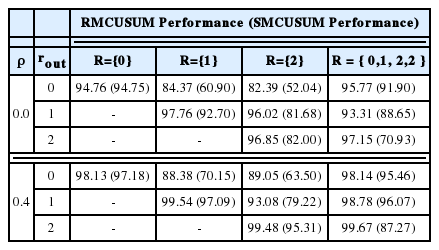
<Table 2>와 <Table 3>은 SMCUSUM과 RMCUSUM 관리도의 공간적 탐지 성과를 비교하여 보여준다. <Table 2>는 두 관리도의 정합률을 퍼센티지로 나타내고 있으며, <Table 3>은 내포율을 퍼센티지로 나타내고 있다. 두 관리도 모두 (<Table 2>의 정합률 면에서나 <Table 3>의 내포율 면에서) 지역적 상관관계가 존재 하는 경우에 더욱 높은 탐지 정확성을 보인다.
RMCUSUM Performance (SMCUSUM Performance)
Comparison of Identification Accuracy 2
<Table 2>의 정합률을 보면
<Table 3>의 내포율 비교 결과를 보면, RMCUSUM 관리도의 상대적 이점이 더욱 뚜렷이 드러난다. 일단, 표에 표시된 모든 경우에서 RMCUSUM 관리도의 내포율이 SMCUSM 관리도의 내포율 보다 크다. 또한 고정된 r값을 사용하는 경우, rout 값에 비해 r값이 커지면 커질수록 SMCUSUM 관리도의 내포율은 큰 폭으로 낙하하는데, 이에 비해 RMCUSUM 관리도의 내포율은 상대적으로 완만한 폭으로 낙하한다. 다양한 r값을 고려하는 경우에도 SMCUSUM 관리도의 내포율은 rout 이 커질수록 낮아지는데, RMCUSUM 관리도의 내포율은 비슷한 값을 유지하거나 오히려 더욱 높아진다. 따라서, 내포율 면에 있어서는 RMCUSUM 관리도가 SMCUSUM 관리도에 비해 더욱 안정된 탐지 성과를 내는 것으로 보인다.
<Table 3>에서 고정된 r값을 사용하는 경우에 SMCUSUM과 RMCUSUM 관리도 모두 rout이 r보다 작을수록 내포율이 감소하는 경향을 보인다. 이는 감시 대상이 되는 지역 군집 내에서 통제 불능 지역 수가 차지하는 비율이 적어질수록, 상대적으로 통제 불능 지역의 식별이 어려워지기 때문인 것으로 보인다. 이를테면, r=2 이고 rout =0인 경우, 군집 내 감시 대상 지역 수는 13개인 것에 비해 통제 불능 상태에 빠진 지역은 1개로 통제 불능 지역을 포함한 군집과 그렇지 않은 군집의 차이가 크지 않아 그만큼 통제 불능 지역 식별에 어려움을 겪는 것으로 해석할 수 있다. 비슷하게, r=1 이고 rout = 0 인 경우, 군집 내 감시 대상 지역 수는 5개인 것에 비해 통제 불능 지역은 1개이기에 상대적으로 통제 불능 지역 식별이 쉬워 r=2 이고 rout = 0 인 경우 보다 탐지 정확성이 높아진 것으로 해석 된다.
<Table 1, 2, 3>의 결과를 종합하여 보면, SMCUSUM과 RMCUSUM 관리도 모두 정확한 rout 의 추정이 가능한 경우에는 r = rout, 그렇지 않은 경우에는 여러 가지 다양한 값을 가질 수 있도록 r을 설정하는 것이 신속성과 정확성 두 측면 모두에서 가장 좋은 결과를 얻을 수 있다는 사실을 알 수 있다.
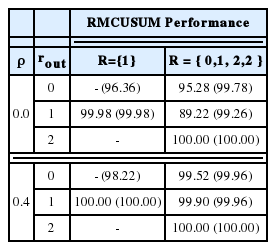
RMCUSUM 관리도는 기본 자료가 어떠한 분포를 따르는지에 상관없이 운영 가능하므로, 본 연구에서는 자료가 다변량 정규분포가 아닌 다변량 포아송 분포를 따르는 경우에 RMCUSUM 관리도의 공간적 탐지 정확성이 어떻게 변화하는지를 알아보기 위해 실험을 진행하고, 그 결과를 <Table 4>에 표시하였다. <Table 4>에서 괄호 밖의 숫자는 정합률을 나타내며, 괄호 안의 숫자는 내포율을 나타낸다. (<Table 4>과 같은 설정 아래에서의 RMCUSUM 관리도의 ARL1 결과 값은 Lee et al.(2015)를 참고하라.) <Table 2, 3>의 결과와 <Table 4>의 결과를 비교하면, RMCUSUM 관리도의 정합률과 내포율이 모두 <Table 4>에서 더 향상 되었음을 알 수 있다. 따라서 RMCUSUM 관리도는 다변량 포아송 분포를 따르는 자료를 위해서도 적용될 수 있으며, 그 공간적 탐지 정확성은 심지어 자료가 다변량 정규 분포를 따르는 경우보다 더 높을 것으로 기대된다.
Identification Accuracy for the RMCUSUM Chart from Multivariate Poisson Data
4. 결 론
지금까지 연구되어 온 많은 관리도는 ARL1값을 기반으로 그 성능을 평가 받아왔다. 하지만 이렇게 탐지 신속성만을 겨루는 것은 시공간 탐지를 위해 설계된 관리도의 비교에는 적합지 않다. 시공간 탐지를 위한 관리도에서는 1) 얼마나 빨리 상태의 변화를 탐지해 낼 수 있는지, 그리고 2) 얼마나 정확하게 상태의 변화를 탐지해 낼 수 있는지가 모두 중요하며, 따라서 이러한 관리도를 비교하거나 평가하기 위해서는 탐지의 신속성과 탐지의 정확성 모두가 함께 종합적으로 분석되어야만 한다.
본 논문에서는 SMCUSUM과 RMCUSUM으로 이름 붙여진 두 개의 다변량 누적합 관리도를 예로 하여 그 탐지의 신속성과 정확성 모두를 실험하고, 그 성능을 비교 분석하였다. 기존의 다른 논문들처럼 ARL1 값만을 근거로 한다면 RMCUSUM 관리도는 SMCUSUM에 비해 그 탐지 성능이 매우 뛰어나다고는 평가할 수 없다. 그러나 RMCUSUM 관리도의 탐지 정확성은 SMCUSUM 관리도의 정확성에 비해 상당히 높으며, 여러 환경의 변화에도 안정적인 탐지 성과를 낸다는 것을 알 수 있다. 따라서 시간적 탐지 성과뿐만 아니라 공간적 탐지 성과를 함께 생각하면 RMCUSUM 관리도는 SMCUSUM에 비해 더 뛰어난 성능을 가진다고 평할 수 있으며, RMCUSUM 관리도는 SMCUSUM 관리도에 비해 초기 설정이 오래 걸리는 대신 사용 가능 환경에 대한 제약이 적어 훨씬 다양한 환경에 적용 가능하므로, 분초를 다투는 급박한 초기 관리한계 설정이 요구되는 경우가 아니라면 RMCUSUM 관리도의 사용을 추천하는 바이다.
SMCUSUM과 RMCUSUM 관리도는 감시 대상이 되는 전체 지역 내에서 하나의 원형 통제 불능 군집만이 생길 수 있으며, 이때 통제 불능 지역 자료의 평균은 일정하게 증가한다는 것을 가정하였다. 따라서 여러 비정형 통제 불능 군집이 나타나거나 통제 불능 지역 자료의 평균이 일정하게 증가하지 않는 경우에는 본 연구와 상이한 결과가 나올 수 있을 것으로 판단되며, 이러한 다양한 상황과 제약을 고려할 수 있는 관리도는 이 후 따로 연구될 필요가 있다. 또한 나아가 자료의 지역적 상관관계만이 아닌 시간적 상관관계도 함께 고려할 수 있는 시공간 탐지 기법이 개발 된다면 후에 시공간 탐지 관리도를 연구하거나 이용하고자 하는 학자 및 사용자에게 더욱 큰 도움이 될 수 있을 것으로 기대된다.
마지막으로, 본 연구에서는 시공간 감시에 적합하다고 알려진 두 다변량 누적합 관리도를 예로 들어 탐지 신속성만을 기준으로 관리도의 탐지 성능을 평가하는 것은 타당하지 못함을 보였다. 허나 대부분의 다른 시공간 탐지 기법들 또한 지금껏 시간적 탐지 성과만을 기준으로 비교되어온 만큼, 기존에 연구되어왔던 시공간 감시 방법론들의 성능을 전반적으로 재검토 및 재평가하는 것도 의미있는 후속 연구가 될 수 있음을 밝혀둔다.