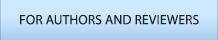우리나라는 신용카드 이용금액이 소비 지출의 절반 이상을 차지하고, 소비 지출의 원천은 소득이므로 소득-지출-신용카드 이용금액 간에 밀접한 관계가 존재할 것으로 예상된다. 이에 소득분포의 속성부터 살펴보고자 한다. 소득금액별 인원수의 확률분포(이하 소득분포)에 대한 연구는 예전부터 존재하였다. Pareto(1897)는 파레토 분포를 이용한 소득분포 모형을 수립하였고, Champernowne(1953)은 감마분포 모형을 제안하였다. 최근에는 Drăgulescu and Yakovenko(2001)가 미국의 소득자료를 이용하여 소득분포가 지수분포를 따름을 밝혔다.

지수분포는 다른 분포들과 달리 파라미터가 하나이므로 해석이 용이하다. 또한 수많은 자연현상을 설명하는 데 유용한 분포라는 사실이 밝혀져 있다. 특히 확률과정의 기본 모형 중 하나인 포아송 과정(Poisson Process)에서 지수분포는 일련의 사건들의 발생시각을 적절히 묘사하는 것으로 알려져 있다. 이처럼 지수분포는 다양한 장점을 갖고 있으므로 국내 소득분포 자료의 확률분포에 대한 탐구는 지수분포를 따르는지의 여부를 검정하는 것으로 한정하고자 한다.

지수분포의 파라미터 λ(>0)는 분포의 모양을 결정하는데, 포아송 과정에서 사용될 때는 ‘단위 시간 동안의 평균사건발생빈도’로 해석된다. 그래서 λ를 rate parameter라고도 부른다. 지수분포의 확률분포함수를 살펴보면 다음과 같다.

국내 소득분포 자료는 국가통계포털(KOSIS)에서 제공하는 ‘근로소득 연말정산 신고 현황(4.2.4)’에서 참조할 수 있다. 이것은 소득금액대별 인원수로서 테이블 형태의 이산형 자료이다. 따라서 식(1)~식(3)에서 χ = 소득금액대(income band)로 정의하는 것이 직관적이다. 그러나 지수분포는 연속형 확률분포이므로 λ가 결정되고 분포 적합이 이루어지면 χ = 소득금액(income)으로 볼 수 있다. 이를 신용카드 이용금액별 사용자 수 확률분포에 적용하면 χ = 신용카드 이용금액으로 정의할 수 있다.

KOSIS 소득자료에는 연간 소득금액대별 인원수가 있고, 급여소득과 비과세소득이 별도 집계되어 있다. Drăgulescu and Yakovenko(2001)는 U.S. Census 데이터인 SIPP 공시자료 중 TPTOINC 항목, 즉 전체 소득 자료를 사용하였는데 KOSIS 자료의 급여소득과 비과세소득을 합친 것과 동등하다고 판단된다. KOSIS 자료는 금액대가 동일 간격이 아니므로 동 간격으로 변형하면 Table 1과 같다.

이것은 1,733만 명에 달하는 원 데이터를 요약 집계한 자료이다. 따라서 소득분포가 지수분포를 따르는지 밝히기 위해서는 카이제곱 통계량을 이용한 적합도 검정을 해야 한다. 카이제곱 통계량은 지수분포로부터 계산한 이론적인 인원수(E)와 실제 인원수(O)를 아래와 같이 연산한 통계량이다.

그런데 적합도 검정은 개체수가 너무 큰 경우 효과적이지 못한데 (Bentler and Bonnet, 1980) 위 자료는 1,733만 명으로 개체수가 매우 크다. 따라서 실제 속성과 관계없이 귀무가설(H₀: E와 O 사이에는 유의적인 차이가 없음)이 기각된다. Cohen(1988)은 이런 경우 효과크기(Effect Size) 척도인 W를 참고하는 것이 적절하다고 설명하고 있다. 효과크기는 개체수의 영향을 배제한 실질적인 차이를 계량하는 척도인데, W가 크면(작으면) 두 집단 간에 실질적인 차이가 크다(작다)는 의미이다.

KOSIS 소득자료에서 비교해야 할 두 집단은 소득금액대별 실제 인원수(O)와 지수분포로 적합하여 산출한 기대인원수(E)이다. 카이제곱 통계량은 Table 2와 같이 계산된다. 식(5)에서  = 개체수 = 17,333,394이다. 이 두 값으 부터 W를 계산할 수 있다. W가 작을수록 두 집단 간에 실질적인 차이가 적어 지수분포에 가깝다고 판정할 수 있다. W값의 해석에 절대적인 기준은 없으나, Cohen은 0.1을 약함(weak), 0.3을 중간(medium), 0.5 이상은 강함(strong)으로 판정할 수 있다고 제안하였다. 따라서 W가 0.1 이하이면 두 집단 간에 실질적인 차이가 아주 작기 때문에 지수분포를 따르지 않는다고 하기에는 설득력이 약하다고 볼 수 있다.

KOSIS 자료의 실제 인당 평균 소득금액은 3.294(천만원)이므로 λ = 1/E(X) = 0.304이다. 만약 원 자료가 0.304를 파라미터로 하는 지수분포에 정확하게 적합되면 O와 E는 서로 같은 값을 갖게 되어 카이제곱 통계량 = 0이 될 것이다. 그러나 사회현상이 이론적인 분포를 완벽하게 따르는 경우는 거의 찾을 수 없다고 할 수 있다. 따라서 KOSIS 자료를 여러 가지 λ 값의 지수분포와 비교하는 민감도분석을 수행하였고, 그 결과 KOSIS 자료는 λ = 0.320일 때 W가 0.0887로 최소가 됨을 알 수 있다. 이것은 Cohen의 약함(weak) 기준을 하회한다. 따라서 Table 2의 O와 E간에 실질적인 차이는 크지 않고, 소득분포는 λ = 0.320의 지수분포와 가깝다고 결론을 내릴 수 있다.

주어진 자료가 지수분포에 적합한 지에 대한 척도가 카이제곱 통계량과 W라면, 반대로 지수분포가 주어진 자료를 얼마나 잘 설명하는지에 대한 척도도 있다. 그것은 상관계수 r로서 특정 확률분포 모형이 데이터와 얼마나 선형적 관계가 강한지를 의미한다. 다만 지수분포는 곡선이므로 실제인원수와 기대인원수에 자연로그를 취하여 계산한다.

식(6)에 따라 계산하면 r = 0.996, p-value = 0.000으로서 지수분포로 산출한 인원수와 소득분포 자료의 인원수가 서로 큰 상관관계를 가짐을 알 수 있다. 그만큼 KOSIS 소득분포 자료를 지수분포로써 적절히 설명할 수 있다는 의미이다.

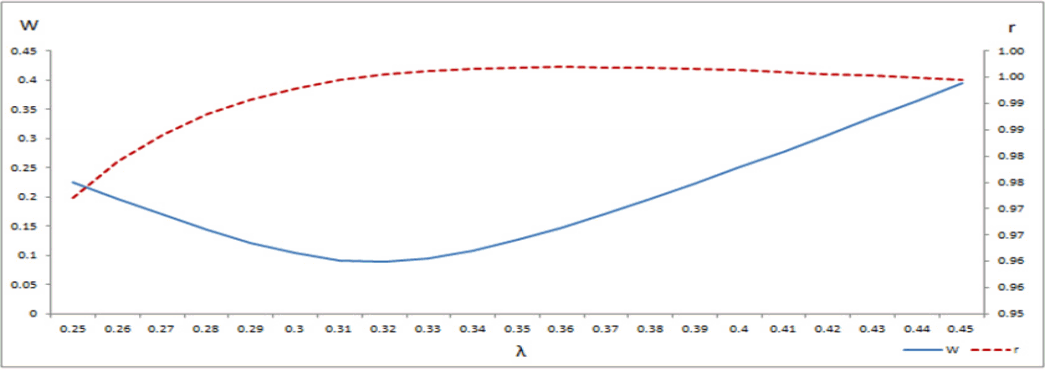
λ를 0.250부터 0.450까지 0.01 단위로 변경하면서 W와 r의 값을 관찰하는 민감도분석 결과, W가 최저가 되는 지점과 r이 최고가 되는 지점은 일치하지 않았다(Figure 1). W가 최저가 되는 지점은 평균 소득금액과 가까운 지점인 λ = 0.320이었으나 r이 최고가 되는 지점은 λ = 0.360이었다(r = 0.997). 그러나 W는 최고-최소값 간에 차이가 큰 반면 r은 큰 차이가 없으므로 W값이 최소가 되는 지점의 λ값을 선택하는 것이 바람직하고, 그에 따라 λ = 0.320을 지수분포의 최종 파라미터로 선택하였다. 적합의 정도는 Figure 2처럼 매우 가깝게 나타났다.

λ = 0.320에서 r = 0.996으로 매우 높은 선형적 상관관계를 유지하고 있다. 따라서 국내 소득분포 자료는 λ = 0.320의 지수분포에 잘 적합되며, 역으로 지수분포로써 충분히 설명할 수 있는 형태라는 결론을 내릴 수 있다. Figure 2에서 보듯 KOSIS 소득자료의 분포와 λ = 0.320의 지수분포를 비교하면 두 분포의 모양이 매우 비슷하게 나타난다. 이로써 국내 소득분포 자료 역시 미국의 사례와 마찬가지로 지수분포를 따른다고 볼 수 있다.

소득과 지출은 비례한다고 가정한다. 일찍이 Keynes(1936)는 소비자는 소득이 증가하면 지출을 증가시키는 경향이 있다고 주장하였다. 이를 바탕으로 경제학계는 ‘소득 = 지출 + 저축’의 관계식을 기본 가정으로 적용해 왔다. 이것은 오랜 전통을 지닌 가정이지만 세월이 지나면서 현재도 계속 유효한 가정인지를 검증해 볼 필요가 생겼다.

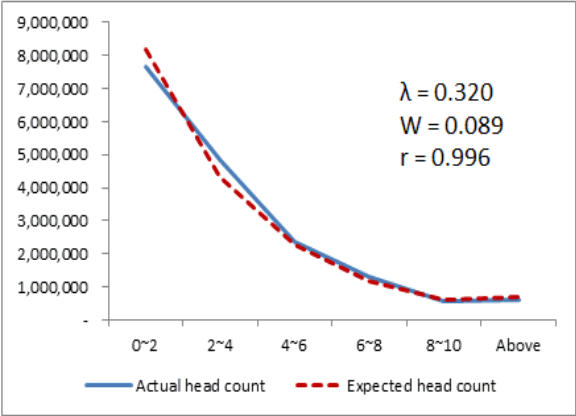
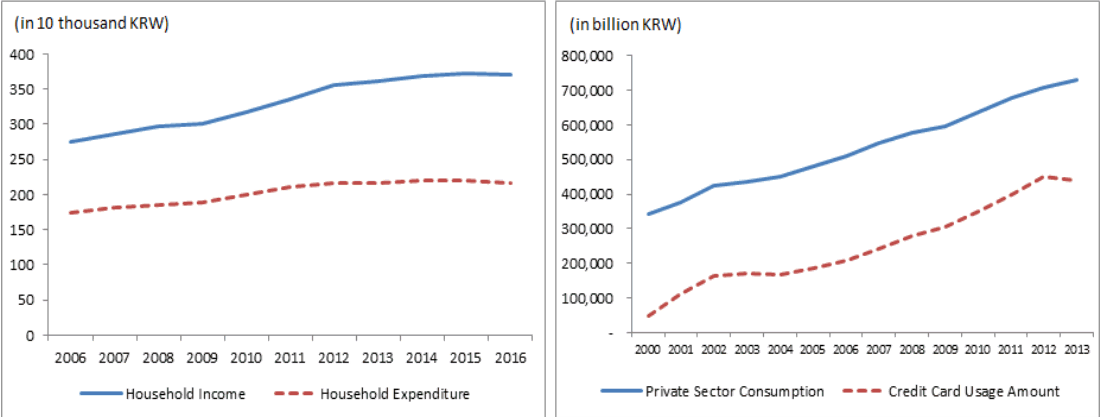
Diacon and Maha(2014)는 세계은행의 자료를 토대로 소득-지출-GDP간의 관계를 연구하였는데, 국가별 소득수준에 따라 다른 경향이 나타났다. 그러나 우리나라가 속한 고소득 국가군에서는 소득과 지출이 대체로 비례하는 것으로 나타났고 이에 따라 Keynes의 가정은 여전히 유효하다고 결론 내릴 수 있다. KOSIS에서 제공하는 월평균 가계수지 자료(2006~2016)를 보아도 국내 소득과 소비지출 역시 서로 유사한 추세로 움직이는 것을 알 수 있다(Figure 3).

소비지출과 신용카드 이용금액 역시 강한 비례관계를 보인다. 이 비례 관계는 세계 어디에서나 공통적일 것으로 추정되지만, 우리나라는 신용카드 사용금액이 민간 소비지출의 절반 이상을 차지하고 있기 때문에 그 비례관계는 더욱 더 뚜렷할 것으로 보인다. 여신금융협회의 자료(CREFIA, 2014)를 보면 2000년 ~ 2013년 민간소비지출과 신용카드 이용금액은 Figure 3과 같이 매우 유사한 추세로 변화하였음을 알 수 있다 (r = 0.992, p-value = 0.000).

전술한 바와 같이 개인별 신용카드 이용금액 자료는 일반적으로 공개되지 않으나 참고할 만한 자료가 일부 존재하므로 그 각각에 대하여 살펴보기로 한다.

(1) UCI repository 데이터

머신 러닝 연구용 데이터를 제공하는 UCI repository에는 독일에서 공개한 실제 데이터(1천건)가 존재한다. 이 데이터에는 21개의 속성값이 있고 그 중 하나가 신용카드 한도금액(이하 신용한도)이다. 신용한도는 신용카드 이용금액의 상한이며 고객별로 상이하게 부여된다. 장기간 금융상품들의 이용 이력으로부터 산출된 신용점수에 근거하므로 개인 소비자별 이용행태의 기준이 된다. 또 월별로 부여되므로 신용한도 분포는 일정 기간 동안 발생한 신용판매 이용금액 분포의 바로미터가 될 수 있다.

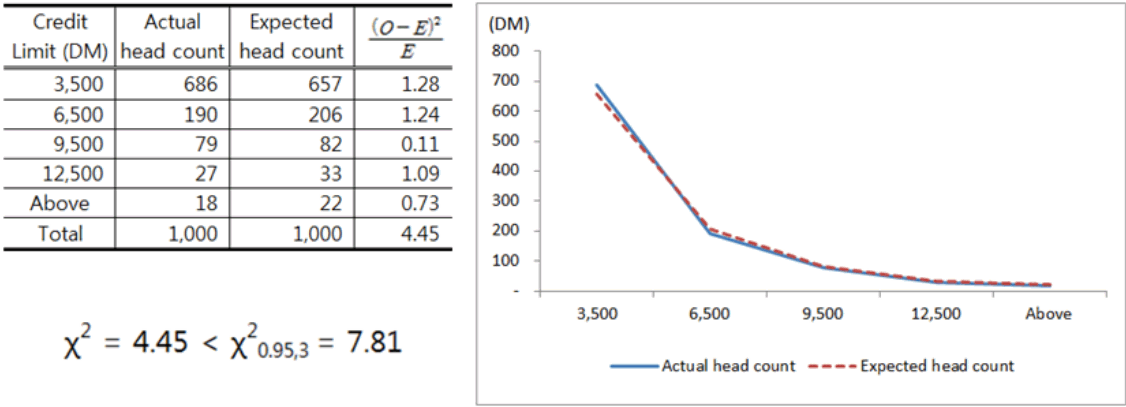
이 데이터는 1천건으로 샘플 크기가 적당하므로 W값을 산출할 필요 없이 곧바로 카이제곱 통계량을 이용한 적합도 검정을 적용하였다. 세부 검정 절차는 RAC (Reliability Analysis Center) 에서 발행한 START Vol.10 (2003)을 참조하였다. 1천건 자료의 신용한도 평균은 3,271이다. 원 데이터에 단위는 명시되어 있지 않으나, EU 출범 이전의 자료이므로 단위는 독일 마르크(DM)로 추정된다.

λ의 초기값은 평균의 역수인 0.003 (1/3,271) 으로 산출하였다. Figure 4에서 보듯이 카이제곱 검정통계량은 4.45이고 이는 유의수준 5%에서의 기각역 하한 χ²_0.95,3 = 7.81보다 작으므로 귀무가설(H₀: O와 E 사이에는 유의적인 차이가 없다)를 기각할 수 없다. 즉, 신용한도의 분포는 λ = 0.003인 지수분포를 따르지 않는다고 볼 수 없으며 이에 따라 추가적인 민감도분석 없이 λ = 0.003을 최종 파라미터로 선택할 수 있다. 이때 카이제곱 분포의 자유도는

로 정의된다. λ라는 1개의 파라미터를 추정했으므로 df = 5-1-1 = 3이 되고, 그에 따라 유의수준 5% 하에서 귀무가설을 기각하기 위한 값은 7.81이 되었다.

(2) 서울시 빅데이터 캠퍼스 데이터

서울시 빅데이터 캠퍼스는 실제 신용카드 이용실적을 기반으로 한 추정매출액을 총 37,045개의 지역 블록단위별로 제공하고 있다. 추정매출액은 두 카드사가 개별적으로 집계한 지역별 매출액을 합산하여 평균한 후 일정한 가중치를 적용, 산출한 값이다. 비록 추정치이기는 하나 실제 매출액에 기반을 두어 매우 현실과 가까운 값이다.

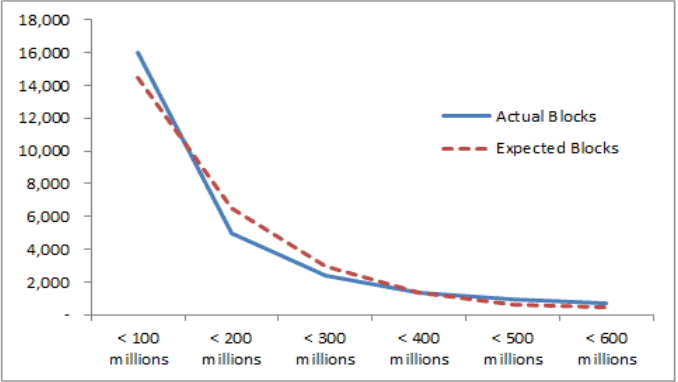
이렇게 산출된 신용카드 추정매출액을 2016년 월별로 집계한 후 계절지수(=해당월 매출/연 평균 매출)를 산출해보면 최소 0.96, 최대 1.10로서 그 차이가 크지 않다 (2월 지수 0.91은 제외함). 따라서 국내 신용카드 이용금액은 연간 고르게 발생한다는 것을 알 수 있다. 그럼에도 명절, 휴가 등으로 인해 계절성이 클 것으로 보이는 시기들을 피해 2016년 6월 매출액을 지역 블록별로 집계해 보았다. 그 결과가 Figure 5이다.

일반적으로 지역별 매출은 개인별 이용금액과는 속성에 차이가 있다. 어떤 지역은 상업시설이 없어 카드 매출이 거의 발생하지 않는 반면 어떤 지역은 상업시설 초밀집 지구로서 높은 매출이 발생할 수 있다. 그러므로 지역별 편차는 개인별 편차보다 훨씬 크다. 또 자료 공급원인 카드사별로 지역 구분 기준이 다를 수도 있다.

이런 사정들을 감안하여 월 매출이 1천만 원 미만인 지역 블록 7,956개와 6억을 초과하는 2,743개 블록은 분포 산출 대상에서 제외하였다. 이렇게 양 극단값을 제거한 후 총 26,346개의 지역 블록에 대해 매출금액대별 블록수분포를 산출해본 결과, 파라미터 λ = 0.80일 때 W = 0.182로 최소값이 된다. Cohen의 기준을 적용하면 중간(medium)보다 약함(weak)에 더 가깝기는 하지만 앞서 살펴 본 소득분포 자료나 신용한도 데이터에 비하면 지수분포에의 적합성이 떨어진다.

그러나 매출금액대가 작은 곳에 많은 지역블록이, 매출금액대가 큰 곳에 적은 지역블록이 분포함으로써 전체적인 분포가 우하향의 L자형 곡선으로 나타나는 점은 실증되었고, 부수적으로 월별 지수가 큰 차이가 없다는 사실도 확인할 수 있었다. 이것은 어떤 집단의 특정 시기의 이용행태를 특정한 지수분포로 묘사할 수 있으면 그 집단의 이용행태는 계속 그 분포로써 묘사할 수 있음을 의미한다.

(3) 시뮬레이션 생성 데이터

마지막으로 시뮬레이션을 통해 생성한 개별 소비자 단위의 이용금액 데이터를 사용하여 지수분포 속성을 살펴보고자 한다. 공인된 신용카드 이용실적 시뮬레이션 모형은 존재하지 않으나, 선행연구 결과들을 활용하고 일부 항목을 국내 상황에 맞춰 보정하여 현실성 높은 모형을 구축하였다.

Schmittlein et al.(1987)은 포아송 과정을 기반으로 일반적인 거래의 빈도와 시점을 생성할 수 있는 모형을 수립하였다. Fan(2016)은 Schmittlein의 모형에 거래금액(신용카드 이용금액)을 생성할 수 있는 수식을 추가하여 신용카드 거래의 시뮬레이션 방법을 제시하였다. 그는 중국의 한 상업은행의 신용카드 매출 자료 44개월분을 이용하여 시뮬레이션 모형을 수립하고 데이터를 검증하였다.

그러나 중국의 신용카드 보급율이 2012년 기준 25%에 불과하므로(Heggestuen 2014) 국내 상황과 동떨어진 측면이 있다. 이러한 부분을 반영하여 최종적으로 정립한 신용카드 이용실적 시뮬레이션 모형은 Table 3과 같다.

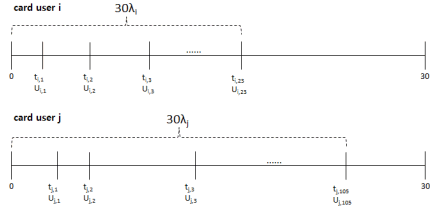
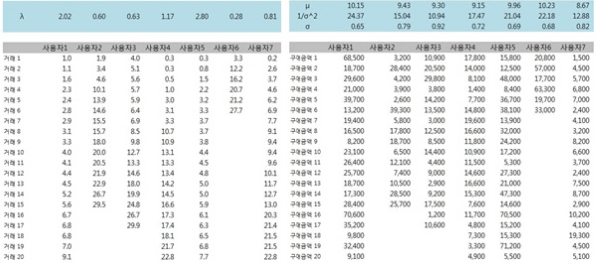
위 모형으로 시뮬레이션을 50회 시행하였다. 각 시행마다 5만명의 고객이 일으킨 신용카드 이용실적을 생성하였고 실험기간은 한 달로 정하였다(T = 30). 서울시 빅데이터 캠퍼스의 자료에서도 보았듯이 국내 신용카드 이용금액은 월별 편차가 크지 않으므로 어느 한 달의 속성을 일반화할 수 있다.

λ_i는 소비자 i의 일평균 신용카드 이용건수이다. 한국은행의 지급수단 이용행태 조사결과 및 시사점(BOK, 2016)에 따르면 카드당 이용건수는 월 평균 16건이다. 이 값을 채택하면 5만개 λ_i의 평균은 0.5 정도가 되어야 한다. 그러나 소비자들이 가장 자주 쓰는 주 사용 카드만을 대상으로 한다면 이보다는 큰 값이어야 하고, 또한 λ_i값이 너무 작으면 0의 매출이 대량 발생할 수 있다. 이런 상황을 종합적으로 고려해서 λ_i의 평균값을 1.5로 결정하였다. λ_i는 감마분포 Gamma(α₁,β₁)을 따르는데 β₁=1로 놓으면 감마분포의 평균이 곧 α₁이 되어 다루기 편리해진다. 따라서 α₁=1.5, β₁=1을 적용하였다.

금융감독원 신용카드 영업실적(FSS, 2017)에 따르면 2016년 한 해 신용카드 이용실적은 596조원, 신용카드 발급매수는 9,564만 매이다. 이중 어느 정도를 실제 사용되는 카드로 보느냐에 따라 카드당 이용금액이 달라진다. 보수적으로 90%를 적용하면 카드당 월 평균 이용금액은 57만 원 정도로 계산된다. U_i,k의 수준을 결정하는 파라미터는 μ_u와 σ_u²인데 μ_u는 사전 모의실험 결과 9일 때 57만 원에 근접한 값이 나왔다. μ_u의 퍼짐의 정도는 σ_u²로 표현되는데, 약 0.25 ~ 0.49일 때 이용금액들이 실제 신용카드 이용금액과 유사하였으므로 본 연구에서는 0.36을 사용하였다.

마지막으로 모형에서 신용카드 이용금액을 보정한 부분을 살펴보기로 한다. 예를 들어 사용자 i의 평균 이용금액(U_i,k)이 상대적으로 높은 수준이라면 μi은 상대적으로 큰 값을 갖는다. 이 때 이용금액의 분산 σ_i²가 매우 작은 값이라고 가정하자. 이것은 U_i,k의 퍼짐의 정도가 작다는 의미이고 따라서 사용자 i의 이용거래는 계속 높은 금액만 발생할 것이다. 이런 경향은 신용카드 보급률이 낮고, 신용카드가 부유층 위주로 보급되어 있는 중국에서는 적절할 수 있다. 그러나 우리나라와 같이 일상생활에서 신용카드를 현금보다 더 많이 사용하고 있는 상황에서 이용거래의 단가는 낮은 금액과 높은 금액이 고르게 분포하는 것이 자연스럽다.

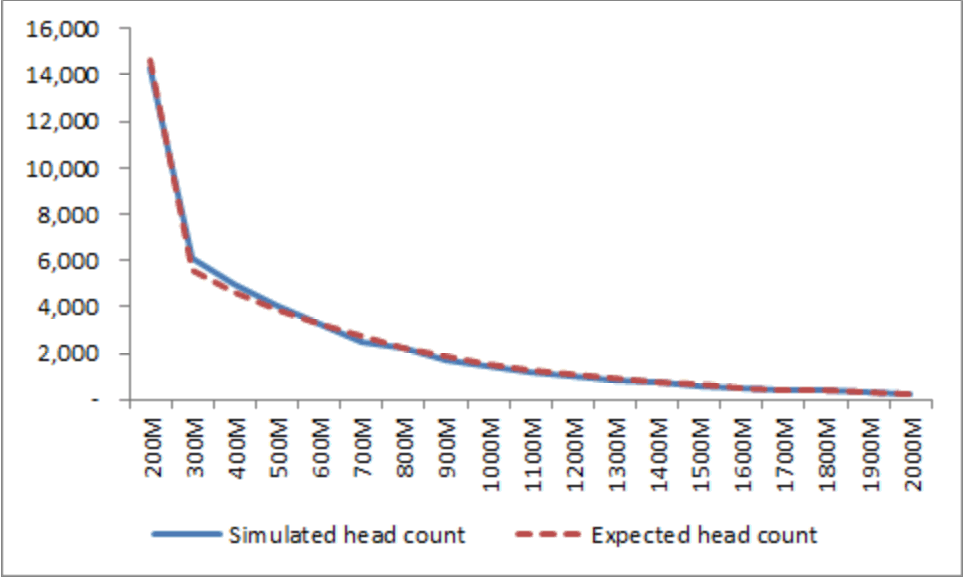
이에 따라 σ_i²가 μi에 비례하는 것으로 모형을 수정하였다. 그렇게 하면 μi값이 클 때 σ_i²도 커져서 작은 금액의 U_i,k가 출현 가능하다. 원 모형에서는 1/σ_i²이 감마분포를 따른다고 가정되는데, 여기서는 새 변수 δi을 도입하고 1/δi이 α₂, β₂를 파라미터로 하는 감마분포를 따르도록 하였다. 1/δi의 값이 C로 결정되면 σ_i² = μi/C로 연산한다. 이렇게 수정한 모형을 이용하여 5만명 씩 50회 시뮬레이션을 한 결과 매 시행마다 Figure 6과 유사한 분포가 나타났다.

소수의 무실적 매출(0의 매출)과 지나친 고금액 매출의 영향을 제거하기 위해 시행별로 상-하위 1.5%씩을 삭제하고 집계한 결과 각 시행마다 Figure 6처럼 지수분포에 가까운 분포를 나타냈고 평균 이용금액은 56만원으로 산출되어 사전 목표 57만원과 비슷한 수준이 되었다. W값은 0.053 ~ 0.071로서 50회 모두 Cohen이 제안한 약함(weak)의 기준인 0.1을 크게 밑돌았다. 이것은 이용금액대별 사용자 수 분포가 지수분포에 아주 가깝다는 의미이다. 한편 지수분포 적합의 척도인 r은 최저 0.994, 최고 0.999로 산출되어 이용금액대별 사용자수는 지수분포로 적절히 묘사될 수 있음이 입증되었다.

신용카드 이용금액대별 사용자 수 자료를 지수분포로 적합시키면 많은 장점이 존재하는데, 그 중 하나는 지수분포는 단일 파라미터를 가지므로 분석 결과의 해석이 쉽고 복잡한 시나리오도 용이하게 분석 가능하다는 점이다. 또 하나 중요한 장점은 그 단일 파라미터가 바로 경영상의 주요 KPI (Key Performance Indicator)로 운용할 수 있다는 점이다.

2.1에서 소득분포에 대하여 역사적으로 다양한 모형이 제시되었음을 기술하였다. 이들 모형은 모두 L자형 곡선이므로 큰 차이는 없다. 그러나 곡선의 만곡률이 조금씩 다르다. 일부 집단의 이용금액별 사용자 수 분포는 지수분포보다 파레토 분포나 감마분포에 더 가까울 수도 있다. 그럼에도 지수분포를 대표 분포로 제시하는 것은 단일 파라미터 모형이므로 해석이 용이하기 때문이다.

지금까지 신용카드 이용금액대별 사용자 수는 지수분포로 설명될 수 있음을 기술하였다. 지수분포와 관련된 식(1) ~ (3)에서 X는 ‘신용카드 이용금액’이므로 이 지수분포는 이용금액의 확률분포라고도 할 수 있다. 또한 이용금액의 평균 E(X) = 1/λ의 관계도 서술하였는데, X가 이용금액이므로 λ는 이용금액과 이용자 수의 속성을 한꺼번에 나타낸다. 그리고 간접적으로 이용빈도와도 연관되어 있다. 따라서 λ는 RFM을 모두 나타내는 파라미터이다.

이런 속성은 λ를 KPI로 운용할 수 있는 여지를 갖게 한다. 즉, λ는 해당 사용자 그룹의 종합적인 이용행태(RFM)를 나타내므로 경영 수준 지표, 목표 달성률 지표, 혹은 서비스품질 지표 등 다양한 KPI로 활용 가능하다. 다른 분포라면 멀티 파라미터의 수많은 조합이 발생하기 때문에 해석이 복잡하여 KPI로 운용하기는 어렵다.

지수분포에의 적합이 가져오는 또 하나의 장점은 다양한 카드 사용자 그룹별로 고유하게 분포를 설정할 수 있는 확장성이다. 지수분포로 특정 사용자 그룹의 이용행태를 설명할 수 있으므로 사용자들을 일정한 기준으로 세분한 집단 역시 지수분포로 설명 가능하다. 대표적인 사례로 카드상품별 이용행태를 지수분포로 적합할 수 있다. 다시 말해 카드상품별로 고유한 λ를 갖는다. 마찬가지로 카드브랜드별 λ도 존재하며 고객군별로도 상이한 λ를 갖는다. 이런 속성은 카드사의 고객관리에 유용하게 활용될 수 있다. λ값만 보면 해당 그룹의 주요 속성들을 한눈에 알아 볼 수 있기 때문이다.

다음으로 이용금액별 사용자 수 분포와 이용금액별 총이용금액 분포의 관계를 그림으로 비교함으로써 서로 어떻게 연관되어 있는지 밝히고자 한다. 그리고 그것을 통해 λ를 좀 더 구체적으로 활용하는 방법을 예시하고자 한다. Figure 7의 왼쪽 그래프는 1만 명의 사용자를 보유한 가상의 A카드의 속성을 지수분포로 묘사한 것이다. 이 상품은 λ = 0.2의 지수분포를 따른다고 가정하자. 금액 단위를 10만원으로 설정했으므로 λ = 0.2는 평균 이용금액이 50만원 정도임을 의미한다.

각 이용금액대별로 중간값을 취하고 이것을 사용자 수와 곱하면 근사적인 총이용금액을 얻을 수 있다. 이렇게 얻은 각 이용금액대별 총이용금액을 이용하여 개인별 평균 이용금액을 구하면 493,400원인데 이론적인 평균값 50만원과 가깝다. 산출 결과 A카드는 월 150만 원 이상 신용카드를 쓰는 고객수가 전체의 4.98%이고 이들이 사용하는 총 이용금액의 비율은 18.53%에 달하는 것으로 나타났다.

오른쪽 그래프는 λ = 0.5의 지수분포를 따르는 가상의 B카드의 상황이다. 평균 이용금액이 20만 원 정도이다. 월 150만 원 이상 신용카드를 쓰는 고객수는 0.04%에 불과하고 이들의 총이용금액 비중도 0.32%에 그치고 있다. 이용금액의 수준이 낮으므로 금액 그래프의 정점이 A카드보다 왼쪽에 치우쳐 있다.

B카드는 A카드에 비해 실적이 저조하므로 당장 폐지해야 할 것 같지만 두 카드는 서로 다른 사용자 집단에 연관되어 있고 그들의 카드 보유 목적이 엄연히 다르므로 두 카드는 모두 존재의 의의가 있다. 예를 들어 A카드는 항공마일리지 카드, B카드는 일반 적립 카드일 수 있는 것이다. 따라서 서로 다른 λ를 갖는 카드상품들과 사용자 그룹들이 공존하고, 카드상품마다 고유의 λ를 갖게 된다.

카드사들은 대부분 VIP 마케팅을 하고 있다. VIP 고객군을 선정하여 전용 카드를 발급하거나 차별적인 혜택을 제공하는 것이다. 발렛 파킹, 프리미엄 매거진, 골프장 콘서트 예약 등 다른 고객군의 사용자들이 이용할 수 없는 혜택을 제공함으로써 고정 고객화 하려는 것이 VIP 마케팅의 전략이다. 따라서 그런 혜택을 향유하는 고객군의 이용행태는 다른 고객군의 행태와 차이가 있을 수밖에 없다.

어떤 사용자 그룹이 λ = 0.05의 속성을 갖고 있다면 평균 이용금액은 1,840만원에 달하고 월 5천만 원 이상 거래를 일으키는 사용자는 8.2%에 달한다. 그리고 이 최상위 사용자들의 총이용금액은 전체 이용금액의 22.5%를 차지한다. VIP 고객군의 평균 이용금액, 최상위 금액대의 사용자 비중, 총이용금액 비중 등은 매우 중요한 관리지표인데 이 주요 지표들이 바로 지수분포의 파라미터 λ 하나만을 이용하여 통합적으로 묘사될 수 있는 것이다.

3.2절에서 기술한 A카드는 상대적으로 우량 고객군이 사용하는 카드이고 B카드는 상대적으로 낮은 이용금액대의 고객들이 사용하는 카드이다. B카드의 인당 평균 이용금액은 204,065원에 그쳐 A카드의 평균 이용금액인 493,400원의 절반에도 미치지 못한다. 이 상황에서 B카드의 인당 평균 이용금액을 30만원까지 올리려면 λ = 0.33은 되어야 할 것이고, 따라서 그렇게 되기 위해서는 각 이용금액대별로 고객수가 어느 정도 변경되어야 하는지 산출해낼 수 있다.

지수분포의 장점은 도달해야 할 인당 평균 이용금액이 정해지면 그 값이 도출되도록 λ를 변경하는 것만으로 각 이용금액대별 사용자 수 분포가 합리적으로 결정된다는 점이다. 어떤 금액대의 고객을 그 다음 금액대로 1명 올리는데 필요한 마케팅 예산이 경험적으로 알려져 있다면 총 마케팅 예산까지도 동시에 결정할 수 있다.

만일 지수분포의 속성을 모른다면 이용금액대별 고객 수를 정할 때 객관적 근거 없이 담당자의 주관적 판단에 의지할 가능성이 크다. 그 경우 고객 분포와 마케팅 예산이 현실과 동떨어지게 산출되거나 효율이 떨어지는 고객군에 많은 예산이 배정될 위험도 있다. 그러나 담당자가 이용금액대별 사용자 수의 지수분포 속성을 알고 있다면 합리적인 변화 수준을 예측할 수 있고 그 변화에 합당한 자원을 배분할 가능성이 매우 높아진다. 이처럼 지수분포는 단일 파라미터의 변동만으로 다양한 시나리오를 분석할 수 있는 장점이 있다.