1. 서 론
오늘날 세계 각지에서는 테러 및 내전 등 다양한 형태의 전쟁이 발생하고 있다. 이에 각국은 새로운 무기체계 및 전력지원체계의 개발을 치열하게 수행하고 있으며 이를 통해 자국 군수산업의 발전 기회를 창출하고자 노력하고 있다. 특히 전력지원체계 분야에서는 자국의 병사를 보호하면서도 효과적인 작전 수행을 수행해야 한다는 패러다임이 도래하면서 방호체계의 경량화 및 방호 수준 강화라는 상충적인 관계를 보완하기 위한 소재 연구가 활발히 이루어지고 있다. 이러한 환경에서 각 국가 및 연구기관에서는 자국 병사들의 생존확률을 높이기 위해 다양한 방호소재를 개발하고 있으며 이러한 방호소재의 성능을 평가하기 위해 선진국 등에서는 다양한 규격을 제작하여 관리하고 시험장을 운영하고 있다. 우리나라의 군에서도 1990년대부터 방호물자에 대한 국방규격을 제정하면서 장병들의 생명을 보호하기 위한 방탄성능 시험기법을 개발하고 국가기관인 국방과학연구소나 육군사관학교 화랑대연구소에서 방탄시험을 진행하여 장병의 생존력 향상에 크게 이바지 해 왔다. 하지만 과학기술의 발달로 인해 최근 무기체계는 급속도로 발전하고 있으며 이에 대한 소재의 기술력도 증가하고 있는 실정이다. 이로 인해 방탄시험 방법도 빠른 주기로 개정되고 다양화되는 추세를 보이고 있다.
방호물자를 도입하는 수요자는 다양한 방탄시험 규격에 근거한 시험결과를 요구하고 있다. 대부분의 방탄시험은 해외 방탄시험 규격에 의거하여 수행되는데, 주로 요구되는 해외 방탄시험 관련 규격을 살펴보면 미국의 MIL-STD-662F(V50 BALLISTIC TEST FOR ARMOR)와 미 국방성 산하 연구소(NIJ : National Institute of Justice)의 NIJ Standard-0101.06(Ballistic Resistance of Body Armor), 유럽연합의 STANAG 4569(Protection Levels for Occupants of Logistic and Light Armoured Vehicles)등이 있다. 이외에도 영국과 중국, 러시아 등에서 개발한 다양한 시험방법이 존재하며, 이와는 별도로 각국에서 작성된 구매요구서에도 각각의 시험 방법이 존재한다. 이처럼 시험방법은 다양하지만 국내에서 이에 대한 성능시험을 수행할 수 있는 기관이나 기업은 부족한 실정이며, 시험방법에 대한 전문가도 부족하다. 현재 우리나라의 시험방법은 대부분 미국의 군사규격인 MIL Spec.을 적용하고 있으나 이에 대한 정확한 해석 및 시험 운영 노하우도 부족한 실정이다. 민간에서 개발 진행 중인 방탄복 및 방탄유리 등 방호소재 및 물자에 대한 시험요구에 비해 국내 방탄성능시험방법에 대한 논의 또한 상대적으로 부족한 실정이라 할 수 있다.
전술하였듯, 개발된 소재의 성능 평가가 해당 시험규격에 의해 진행되고 평가되기 때문에 시험 방법에 관한 연구는 중요하다고 할 수 있다. 그럼에도 불구하고 국내에서 수행되고 있는 방탄 관련 연구는 소재의 성능 향상에 국한되고 있으며 방탄 시험 방법에 관한 연구는 거의 전무하다고 할 수 있다. 기존의 연구를 살펴보면 세라믹, 아라미드 섬유의 조합에 따른 방탄성능 향상 등(태원석, 김건인, 2013; 김종환, 신윤호, 2017)에 관한 것이 주를 이루고 있어 방탄성능시험 절차에 대한 연구보다는 재료의 방탄성능에 대한 연구가 주를 이루는 실정이다. 일부 수행된 방탄시험에 관한 연구를 살펴보면 최윤대(2005)는 방탄시험에 대한 기술 동향에 대해 연구하였으나, 해외 시험규격에 대한 일반적인 해설로 구체적인 시험 방법의 설명 및 개선사항 등에 대한 언급은 부족했다. 육군사관학교(2014)는 국내/외 방탄 시험평가 관련 주요 규정과 국외 선진국의 시험평가 시사점을 바탕으로 국내 방탄/지뢰방호 시험평가 관련 체계 및 보완사항을 제시하여 기존보다는 좀 더 나은 결과를 보였다. 구승환, 김태현, 송승환, 박상원(2016)은 국내 방탄시험 운영 경험을 바탕으로 해외와 비교한 뒤 시험 방법의 선진화 방안을 제시하였으나 이 또한 기초적인 수준에 불과했다.
방탄시험에 대한 관련연구로 국내에서는 김종환, 김제용(2014)은 소구경탄자의 충돌속도 추정방법을 제안하기 위해 미국의 검증된 PRODAS의 데이터를 기반으로 MIL-STD-662F 방법의 충돌속도 추정 값과 제안한 방법의 충돌속도 추정 값을 비교하고 분석하였다. 그 결과, 일부 속도구간에서는 MIL-STD-662F의 방법보다 오차가 크지만 방호한계속도 산출이 가능하다는 점과 대부분의 속도구간에서는 MIL-STD-662F보다 그들이 제안한 방법이 오차가 작다는 점을 도출하였다. 김종환, 조성식(2016)은 재귀적 베이시안 필터를 적용하여 소화기 탄의 충돌속도를 추정하였는데, 연구결과 기존의 속도 변화량 방법을 통해 얻어진 충돌속도 보다 베이시안 필터를 적용한 추정법이 분산과 평균제곱근 편차, 퍼센트 바이어스에서 개선되었음을 통계적으로 확인하였다. 이와 같이 일부 방탄성능시험 기법에 대한 선행연구에서는 충돌속도의 추정 방식에 대한 것이 주를 이루고 있다. 하지만 정확한 충돌속도를 추정하더라도 결과 값인 V50을 산출하지 못하는 경우 충돌속도를 추정한 것이 무용지물이 된다. 따라서 V50을 산출함에 있어서 오류를 최소화하기 위한 연구가 필요하다.
V50을 산출하기 위한 해외 연구를 살펴보면 Riley, Rice, Forster(2012)는 V50 시험에서의 합리적인 불확도 산출에 대해 연구하였다. 일반적으로 많은 사격을 진행할 경우 확률적으로 정확한 V50 값을 추정할 수 있지만 실제로는 무한한 사격이 불가능하기에 산출하기 위한 적정 사격 발수 등을 살펴보기 위해 몬테카를로 시뮬레이션을 사용하여 초기 탄속, 사격 절차(범위), 사격 발 수, 시료의 성능이 V50 추정의 불확실성에 미치는 영향을 평가하였다. 연구결과, V50 추정의 불확실성은 적은 수의 사격을 실시할 때 증가하며, 불확실성을 줄이기 위해서는 48 ~ 60 회 이상의 사격 이 필요하다고 주장한다. 이들은 향후 연구에서 대체 시험 방법의 연구가 필요함을 언급하였으며, 정적 시료 수와 최소의 사격을 위한 전략 수립이 중요하다고 하였다. Johnson, Freeman, Hester, Bell(2014)은 미 국방성(DoD)에서 수행된 V50 산출절차, 추정치, 종료 기준을 검토하고 비교하였다. 이들 역시 몬테카를로 시뮬레이션을 사용하여 Up and Down Method(UD), the Langlie Method(LM), the Delayed Robbins Monroe Method(DRM), Wu's three-phased approach(3POD), Neyer's Method(NM), the Robbins Monroe Joseph Method(RMJ), K-in-a-row(KR) 시험 방법의 V50 과 V10 산출 결과에 대한 편차를 비교하였다. 연구결과, V10의 편향을 줄이는 가장 효과적인 방법은 RMJ, DRM, 3POD로 나타났으며, 샘플 크기가 큰 경우(20개 이상)에서 DRM이 불규칙하게 수행된다는 점을 지적했다. 또한 V50 추정에서는 3POD 방법이 가장 낮은 편차가 발생한다고 주장하였다. 마지막으로 미국방부에서 제시하는 종료 기준을 적용하는 경우 모든 방법이 UD 방법보다 낮은 편향을 보인다고 하였다. 이는 UD 방법론을 사용하는 모든 시험 절차에 개선이 가능함을 시사한다. Mauchant, Rice, Riley, Leber, Samarov, Forster(2011)는 실제 수행된 실험 데이터를 토대로 Logit, Probit, Log-log response models의 세 가지 회귀 모델을 적용하여 V50 산출 결과를 평가하고 비교하였다. 연구결과, 세 가지 모델 모두 유사한 결과를 나타낸다고 주장하였으며, Logit과 Probit 모델에서 일관적으로 좋은 결과가 나타난다고 하였다.
국방기술품질원은 정부에서 운영하고 있는 방탄성능 시험기관으로 2015년부터 시험을 수행하고 있다. 본 연구는 몇 년간 실제 시험운영 과정에서 발생하는 문제점을 해결하기 위한 것에서 시작되었다. 국방기술품질원에 의뢰된 방탄성능 시험 중 가장 많이 의뢰되는 시험측정 항목은 MIL-STD-662F 규격의 V50 산출과 NIJ Standard-0101.06의 P-BFS(Perforation and Backface Signature Test : 후면변형 측정)이다. 국내/외에서 시험되고 있는 방탄소재의 대부분은 V50을 측정하게 되어 있기 때문에 본 연구에서는 이를 중심으로 살펴보고자 한다. V50은 방탄소재가 특정 탄자에 의해 관통될 확률이 50%가 되는 속도를 의미하는 것으로 쉽고 단순하게 계산할 수 있다는 장점을 가진다. 이러한 장점 때문에 다양한 품목의 방탄성능 시험평가에 사용되고 있으나 소재의 특성으로 인하여 관통과 미 관통이 일정하지 않게 발생할 경우, V50의 산정을 위한 속도분포가 기준치를 초과하는 경우 등 특정상황에서는 산출이 불가능하다는 치명적인 단점을 가지고 있다. 따라서 실제 시험과정에서는 V50 산출이 불가능한 경우가 종종 발생한다. 이러한 경우를 대비하여 적정 산출방안을 적용할 필요가 있지만 아직까지는 이에 대한 연구가 부족한 실정이다. 이에 본 연구에서는 실제 방탄성능시험을 운영함에 있어서 V50 산출이 불가능한 문제가 발생할 경우 이를 해결할 수 있는 방안으로 로지스틱 회귀모형을 사용한 V50 산출 대안에 대해 연구하고자 한다.
본 논문의 구성은 다음과 같다. 제 2장에서는 V50을 추정하기 위한 방탄성능 시험방법과 관련 이론에 대한 고찰을 수행하며, 제 3장에서는 시뮬레이션의 설계 및 시나리오에 대해 설명한다. 제 4장에서는 본 연구에서 제시하는 방법론을 사용한 추정치와 기존의 방법을 사용한 V50 산출 결과를 비교하고 특수상황을 가정한 시뮬레이션을 수행하여 결과를 분석한다. 마지막으로 제 5장에서는 본 연구의 결과를 요약하고 의의와 한계점 및 향후 연구 방향을 제시한다.
2. 이론적 배경
2.1 V50 방호한계 측정 개념
V50이란 일종의 방호한계를 지칭하는 용어로 미 군사규격 ‘MIL-STD-662’와 유럽의 규격 ‘NATO STANAG 2920’에 명시되어 있다. 이에 대한 뜻을 살펴보면 “Velocity 50%”의 약자로 ‘방탄재가 관통될 확률이 50%인 속도’, 즉 해당 방호 소재의 방호 임계 수준을 의미한다. 따라서 V50은 50%의 확률로 완전관통(CP : Complete Penetration)할 수 있는 충격속도를 의미하며, V0는 모든 탄두가 완전관통이 일어나지 않을 최대속도를 의미한다. 여기서 완전관통이란 사격 후 탄두 및 파편에 의해 방탄재 뒤에 설치한 확인판이 관통되어 빛이 통과하는 구멍이 발생하는 경우를 말하며, 부분관통(PP : Partial Penetration)은 완전관통이 아닌 모든 경우를 지칭한다.
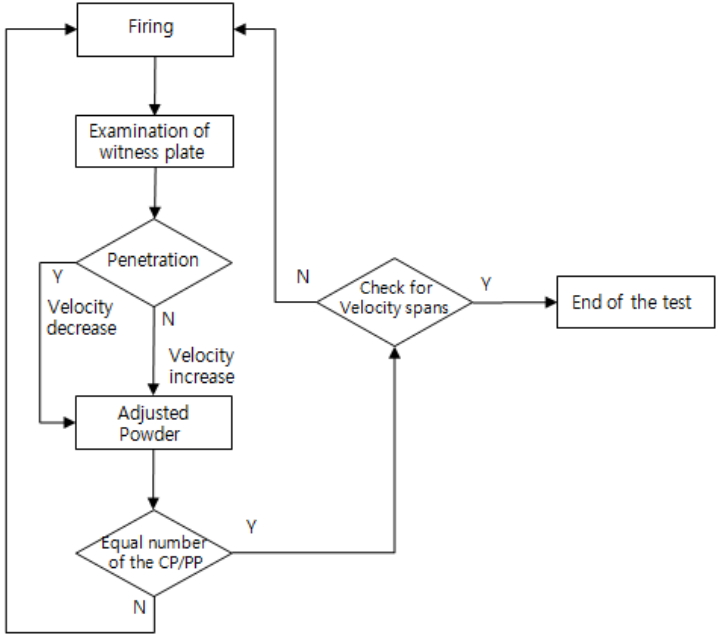
V50을 산출하기 위해서는 Figure. 1과 같은 절차로 시험하는데 해당 탄의 추진제 양을 조절하여 속도를 ‘Up-and-Down’ 방식으로 변화시키며 방탄재에 해당 탄으로 사격을 가해 ‘동일한 수의 가장 높은 부분관통 속도와 가장 낮은 완전관통 속도의 평균’으로 구한다. 이때의 완전 및 부분관통의 속도분포(Velocity Spread)는 사용되는 값이 일정 범위 이내에 들어야 정상적인 V50 시험수치로 인정하며, 해당 수치는 Table 1과 같다.
V50을 산출하기 위한 시험 방법을 세부적으로 살펴보면, 첫발은 규격치보다 22.5 ~ 30 m/s 속도가 더 나오도록 추진제를 조절하여 발사한다. 만일 첫발이 완전관통이면 추진제 양을 줄여 속도를 15 ~ 30 m/s 낮추어 부분관통을 유도하고, 만일 첫발이 부분관통이면 추진제 양을 늘려 속도를 15 m/s 증가시켜 완전관통을 유도한다. 이후부터는 전술한 것과 같은 방법으로 추진제 양을 조절하여 속도를 15 m/s 범위로 증감하면서 완전 및 부분관통 유도를 되풀이 한다. 이와 같은 방법을 계속하여 동일 수의 가장 높은 부분관통 속도와 가장 낮은 완전관통 속도를 선정하여 평균한 것을 V50 값으로 산출한다. 예를 들어 완전관통 5발, 부분관통 5발로 산정할 경우 Table 1에 따라 속도분포(Velocity Spread)가 38.1 m/s 범위 내에 존재해야 하며, 이를 넘으면 다시 추가사격을 진행하여 7개의 가장 높은 부분관통(PP)속도와 7개의 가장 낮은 완전관통(CP) 속도를 선정하여 V50을 산출한다. 이때 선정된 14발(완전관통 7발, 부분관통 7발)의 속도분포는 45.7 m/s범위 내에 존재해야 하며, 만일 속도분포가 45.7 m/s범위를 넘으면 재시험해야 한다. V50을 구하는 식은 다음과 같으며 자세한 설명은 3.1.1항에서 다루기로 한다.
2.2 로지스틱 회귀모형
로지스틱 회귀분석은 비선형 관계에서 독립변수와 종속변수 사이의 함수관계를 설명할 수 있는 방법론으로 로지스틱 회귀분석은 이분형 로지스틱과 다항 로지스틱으로 구분할 수 있다. 이분형 로지스틱 회귀분석은 일반적으로 사용되는 회귀분석과 같이 n개의 독립변수와 1개의 종속변수 간의 관계를 표현하는 기법으로 일반 회귀분석과의 차이점은 로지스틱 회귀분석에서의 종속변수는 0 또는 1의 두 가지 값만을 갖는다는 점이다. 로지스틱 회귀모형의 해석을 위해 오즈비(odds ratio)를 사용하는데, 우도(odds)는 어떤 사건이 발생할 확률을 예측하는 것이다. 따라서 확률이 0.5(50%)보다 크면 해당사건이 발생하는 것으로 예측하며, 반대일 경우 해당사건이 발생하지 않는다고 예측한다.
방탄성능시험의 수행 시 결과 값은 완전관통 또는 부분관통의 두 가지 경우만 존재하므로 로지스틱 회귀분석의 종속변수로 사용가능하다. 여기에 독립변수로 탄속을 사용하면 탄속에 따른 관통여부에 대한 관통여부를 예측할 수 있다. 즉, 실제 수행한 속도와 관통여부 데이터를 토대로 도출된 수식에 탄속을 대입할 경우 확률 값으로 결과가 도출되기 때문에 확률이 50%가 되도록 탄속 값을 역추적하면 정확한 V50을 산출할 수 있다는 가정을 할 수 있다. 따라서 본 연구에서는 탄속을 독립변수로 하고 이로 인한 관통 발생여부를 종속변수로 하여 V50 값을 예측하는데 로지스틱 회귀분석을 사용하고자 한다.
3. 연구 설계
3.1 시뮬레이션 설계
3.1.1 설계 시 고려사항
본 연구에서는 ‘MIL-STD-662F’ 방탄 시험 규격에 의거하여 V50을 산출하는데 있어서 로지스틱 회귀분석 기법을 사용한 개선방법을 제안하고자 한다. 앞 장에서 살펴보았듯 V50은 완전관통과 부분관통이 균일하지 않게 발생할 경우와 속도의 최대/최소 범위가 규격에서 정한 기준치를 초과할 경우 산출이 불가능하다는 단점을 가지고 있기 때문에 본 연구에서는 방탄성능시험을 운영함에 있어서 V50을 산출할 수 없는 문제가 발생할 경우 이를 해결할 수 있는 대안으로 로지스틱 회귀분석을 사용한 V50 산출방법을 제시하고자 한다.
V50 산출 시험을 진행함에 있어서 실제 발생하는 특징은 다음과 같다. 첫째, 각 사격완료 후 완전관통과 부분관통 발생을 확인한 뒤 추진제를 조절하여 속도를 증감시킨다. 여기서 속도를 증가시킬 경우 일반적으로 추진제의 양을 증가시키게 되는데, 일반적으로는 추진제의 양과 탄속이 비례하지만 그렇지 않은 경우도 존재한다. 이는 해당 탄자의 특성 및 세부적인 환경요인 등 다양한 탄도학적 요인이 작용하기 때문이며 해당 탄약에서 추진제를 덜어내는 과정을 거치기 때문에 탄피 내에서 완전 연소가 일어나지 않는 경우도 있기 때문이다. 여기에 추진제 양의 조절은 0.001 g ~ 0.01 g 단위로 미세한 수준에서 이루어지기 때문에 의도한 것과 같이 정확한 탄속을 만들어내는 것이 어렵다. 둘째, 각각의 소재가 갖는 물성이나 특성이 다르고 관통 확률이 50%로 추정되는 속도를 산출하는 시험이기 때문에 추정치보다 낮은 속도라고 무조건 부분관통이 발생하는 것이 아니며, 반대로 추정치보다 높은 속도에서 완전관통이 발생하는 것도 아니다.
이러한 특징으로 인해 실제 환경을 반영하기 위한 몇 가지 고려사항이 도출될 수 있으며, 본 연구에서 사용되는 시뮬레이션에 대한 가정은 다음과 같다. 첫째, 해당 탄에 의한 해당 시료의 V50 값은 700 m/s이다. 둘째, 각 사격 후 탄속 700 m/s 이상에서는 완전관통, 이하에서는 부분관통이 발생하는데 이 과정에서 10%의 확률로 반대의 현상이 발생한다(돌연변이). 셋째, 해당 시료는 특정 탄속 이하에서는 100% 방호한다. 반대로 특정 탄속 이상에서도 100% 관통하게 되는데 여기에서 특정 탄속은 시나리오에 따라 %형태로 증감된다. 넷째, 탄속의 가감은 시나리오에 따라 %형태로 증감된다. 다섯째, 계산 편의상 해당 시료에 대한 사격은 10회만 수행한다. 여섯째, 시편에 가해지는 탄자의 속성(무게, 형상 등)은 모두 동일하다.
Table 2는 본 시뮬레이션의 가정에 대한 V50 산출과정을 예로 나타낸 것이다. 첫 사격 이후 CP 발생으로 두 번째 사격은 속도를 –2% 감소시켜 사격한다. 두 번째 사격 결과는 PP로 사격 결과 CP가 1개, PP가 1개 도출되었다. Figure 1 및 Table 1을 살펴보면 최소 동일 수의 CP와 PP의 개수는 2개 이상이므로 3번째 사격을 실시한다. 3번째 사격은 속도를 증가시켜 사격하였으나, 돌연변이 발생으로 700 m/s임에도 불구하고 PP가 발생하였다. 따라서 동일 수의 CP와 PP의 개수가 되지 않았기 때문에 4번째 사격을 실시한다. 4번째 사격결과 또한 동일 수의 CP와 PP의 개수가 아니기 때문에 5번째 사격을 실시한다. 5번째 사격 결과 CP가 2개, PP가 3개 발생했다. 이 때, 가장 낮은 CP 2개와 가장 높은 PP 2개의 값을 사용하면 V50을 산출할 수 있다. 하지만 속도의 범위차가 Table 1에서의 허용범위보다 크기 때문에(728 – 686 = 42) CP와 PP의 개수가 2개인 ‘2 & 2’로 V50을 산출할 수 없다. 따라서 6번째 사격을 진행한다. 6번째 사격에서는 CP가 나타났기 때문에 ‘2 & 2’ 또는 ‘3 & 3’를 사용하여 V50을 산출할 수 있다. Figure 1의 절차에 의하여 1번, 3번, 4번, 6번을 사용할 경우 범위 14 m/s 이내로 종료조건을 만족하며, V50이 산출가능하다. 따라서 V50 값은 1번, 3번, 4번, 6번 탄속의 평균 값인 706.75 m/s가 된다.
3.1.2 시뮬레이션 설계
본 연구에서는 시뮬레이션 구현을 위한 Tool로 Microsoft MS Excel을 활용했으며, 로지스틱 회귀분석 모델은 Visual Basic을 사용하여 구성하였다. 사용자 정의 폼을 사용하여 각 시나리오 별 수치를 직접 입력할 수 있도록 설정했으며 매크로를 사용하여 각각의 시험에서 발생되는 10개의 탄속 데이터를 별도의 산출 값으로 추출하였다. 이외에도 각각의 실험횟수, 탄속 평균, 방어(성공)확률, 방어 실패 하위 3개 평균속도, 방어 성공 상위 3개 평균속도, V50에 사용된 결과 값의 속도분포, 기존대로 추정된 V50 값, 로지스틱 회귀모형을 통해 추정된 V50 값, 추정치과 기존값의 차이, 로지스틱 계수 및 상수를 산출 값으로 나타나도록 설계하였다.
본 연구에 기초가 되는 V50 산출자료는 국방기술품질원 신뢰성시험센터 다릿골시험장에서 수행된 '17년 2월 ~ 18년 7월 간 시험에서 발생된 실제 데이터를 토대로 하고 있다. 실 데이터는 000건의 Cal.22 모의파편탄을 사용한 V50 시험 결과이며, 본 연구를 위해 평균적인 시험결과를 적용하여 V50이 700 m/s인 시료를 가정했다. 또한 추진제의 조절 비율 또한 실제 조절된 탄속 결과에 의거하여 가감 비율을 2%와 5%로 산정하였다. 또한 1회당 최대 사격할 수 있는 발수는 10발로 가정했으며, 관통의 역전현상이 발생할 확률은 10%로 정하였다. 시뮬레이션에서 각 회 차의 탄속은 MIL-STD-662F 규격에서 정하는 충돌속도라 가정하고 V50 값을 산출한다.
본 시뮬레이션 과정에서 V50 값을 예측하기 위해 난수 생성으로 탄속을 발생시키고 역전현상을 포함하여 700 m/s를 기준으로 완전관통과 부분관통을 각각 0과 1로 하는 이분형(binary variable) 더미변수를 만들었다. 해당 10회분의 사격을 가정한 뒤 로지스틱 회귀분석을 실시하고 관통확률을 예측하였다. 로지스틱 회귀분석은 분석결과 값이 0.5보다 크면 관통할 것으로 예측하며, 0.5보다 작으면 방호하는 것으로 예측하기 때문에 도출된 수식을 토대로 엑셀 해찾기 기능을 사용하여 확률이 50%가 되는 V50 값을 역으로 산출하였다. 시뮬레이션은 각 시나리오 당 1,000회 수행하였으며, 모형의 적합성은 –2log 우도를 이용하여 판단했다.
3.2 시나리오 설계
본 연구에서는 기존의 V50 측정방법과 개선된 V50 측정방법을 시뮬레이션을 통해 비교분석하고자 총 6개의 시나리오를 구성했으며, 각각의 시나리오는 시료가 갖는 균질성과 탄속 변동률의 차이로 구분된다. 시료의 균질성을 시나리오로 선정한 이유는 실제 발생하는 시료의 균질성 오류로 인한 V50 산출 불가 상황을 가정한 것이며, 탄속의 변동률은 실제 사격 후 발생하는 변동률을 토대로 비율을 추정한 것이다. 각 탄속 변동률의 표준편차를 2%(약 15 m/s)와 5%(약 30 m/s)로 정한 이유는 실제 산출된 데이터를 토대로 편차를 살펴본 결과가 최소 14.2 m/s, 최대 29.8 m/s로 나타났기 때문이다. 실질적으로 시료의 균질성이 확보되지 못한 경우나 시험 시 탄약이나 시험자의 휴먼 에러 등으로 인하여 발생하는 오류로 인해 V50의 측정에 애로사항이 발생하기 때문에 이와 같은 시나리오는 현실을 충분히 반영하고 있다고 볼 수 있다. 개선된 V50 측정 방법과 기존 V50 측정방법과의 비교분석을 위해 설계된 시나리오는 Table 3과 같다.
4. 실증분석
4.1 시뮬레이션 결과
본 연구는 Table 3에 따라 6가지 시나리오별 시뮬레이션을 실시한다. 각 시뮬레이션은 10번의 사격 데이터를 가지며, 1,000회의 반복으로 얻어진 결과 값을 나타낸다. 기존의 V50 산출방법과 개선된 V50 산출방법으로 산출된 결과가 유사한지를 비교하기 위해 V50 값을 추출하였으며, 실질적으로 산출이 불가능한 경우가 얼마만큼의 비율로 발생할 수 있는지 살펴보기 위해 기존의 V50 산출방법으로 추정이 불가능한 개수를 산출하였다. 최종적으로 각각 시나리오별 기존 V50 산출 결과와 개선된 방법으로 산출한 V50 간의 차이를 비교했다.
먼저 시나리오 1은 기존의 방식으로 추정할 수 없는 V50 값이 11개로 나타났다. 이들 값을 제외하고 기존의 방식으로 산출된 V50은 평균 698.15 m/s, 개선된 방식으로 산출된 V50은 평균 700.45 m/s로 나타났다. 추정치와의 차이는 +2.30 m/s로 나타났으며, 본 연구에서 가정한 V50 값인 700 m/s에는 개선방식이 기존의 방식으로 산출한 V50 값보다 더 근접한 것을 알 수 있었다. 시나리오 2의 경우 기존의 방식으로 추정할 수 없는 값은 440개로 나타났으며, 이는 전체의 44%를 차지한다. 이는 탄속 범위의 속도분포가 크기 때문에 기준을 초과한 것으로 사료된다. 산출 불가능한 값들을 제외하고 기존의 방식으로 산출된 V50은 평균 697.18 m/s, 개선방식으로 산출된 V50은 평균 697.20 m/s로 나타났다. 추정치와의 차이는 +0.02 m/s로 나타났으며, 본 연구에서 가정한 V50 값에는 제안한 방식이 기존 방식으로 산출한 V50 값보다 더 근접한 것을 알 수 있었다.
시나리오 3의 경우 기존의 방식으로 추정할 수 없는 값은 7개였으며, 이들 값을 제외하고 기존의 방식으로 산출된 V50은 평균 698.20 m/s, 개선된 방식으로 산출된 V50은 평균 703.55 m/s로 나타났다. 추정치와의 차이는 +5.35 m/s로 나타났으며, 본 연구에서 가정한 V50 값에는 기존의 방식이 제안한 방식으로 산출한 V50 값보다 더 근접한 것을 알 수 있었다. 시나리오 4의 경우 기존의 방식으로 추정할 수 없는 값은 436개로 전체의 44%가 산출불가로 나타났는데, 이는 시나리오 2와 마찬가지의 이유로 사료된다. 산출 불가능한 값들을 제외하고 기존의 방식으로 산출된 V50은 평균 697.66 m/s, 개선된 방식으로 산출된 V50은 평균 697.70 m/s로 나타났다. 추정치와의 차이는 +0.05 m/s로 나타났으며, 본 연구에서 가정한 V50 값에는 제안한 방식이 기존의 방식으로 산출한 V50 값보다 더 근접한 것을 알 수 있었다.
시나리오 5의 경우 기존의 방식으로 추정할 수 없는 9개의 값들을 제외하고 기존의 방식으로 산출된 V50은 평균 698.32 m/s, 개선된 방식으로 산출된 V50은 평균 698.37 m/s로 나타났다. 추정치와의 차이는 +0.05 m/s로 나타났으며 본 연구에서 가정한 V50 값에는 제안한 방식이 기존의 방식으로 산출한 V50 값보다 더 근접한 것을 알 수 있었다. 시나리오 6의 경우 기존의 방식으로 추정할 수 없는 값은 486개로 전체의 48.6% 수준이다. 산출 불가능한 값들을 제외하고 기존의 방식으로 산출된 V50은 평균 696.98 m/s, 개선된 방식으로 산출된 V50은 평균 697.00 m/s로 나타났다. 추정치와의 차이는 +0.03 m/s로 나타났으며, 본 연구에서 가정한 V50 값에는 제안한 방식이 기존의 방식보다 더 근접한 것을 알 수 있었다.
각 시나리오에서의 속도 분포의 평균을 살펴보면 시나리오 1, 3, 5의 경우 탄속 범위의 차이가 작기 때문에 약 12 m/s 내외로 나타나는 것을 확인할 수 있었으며, 시나리오 2, 4, 6의 경우 탄속 범위의 차이로 인해 약 21 ~ 22 m/s의 수준을 보이는 것을 확인할 수 있었다. 또한 탄속 범위의 차이에 따라 회귀식이 다르게 도출되었는데, 탄속 범위의 평균이 약 15 m/s 수준으로 작을 때에는 -0.32x(탄속) + 222.76으로 나타났으며, 탄속의 범위의 평균이 약 30 m/s 수준으로 클 때는 -0.21x(탄속) +146.7로 나타났다.
4.2 시나리오별 t 검정 결과
앞 절에서는 시뮬레이션에 따른 회귀식 도출 및 각 시나리오별 기존 방식과 개선된 방식으로 도출된 V50 값에 대해 살펴보았다. 결과를 살펴보면 기존의 방식으로 산정한 결과와 개선된 방식으로 산정된 결과 값이 미미한 차이를 나타내고 있다. 시나리오 1에서의 기존 추정방법으로 산정한 V50의 결과 값과 본 연구에서 제안한 산정 방법을 적용하여 산정한 값은 2.3 m/s의 차이가 존재하는 것을 확인하였다. 하지만 개선된 방식으로 추정이 가능하다는 것을 입증하기 위해서는 이에 대한 통계적 유의성의 추가 검증이 필요하다. 그 이유는 개선된 방식으로 산정된 결과 값과 기존 방식의 결과 값이 통계적으로 유의한 차이가 없다면 V50을 산출할 수 없을 경우 앞서 도출한 로지스틱 회귀식에 대입하여 V50 값을 추정하는 것이 가능하다는 것을 입증할 수 있기 때문이다. 따라서 본 절에서는 각 시나리오에서 도출된 기존의 방법대로 산정한 결과 값과 개선된 방법으로 산정한 결과 값이 유사한지에 대해 독립표본 t검정을 사용하여 비교한 뒤 유의한 차이의 여부를 검정하였으며 검정 결과는 Table 5와 같다.
t검정 결과, t값은 .990, 유의수준은 .322로 나타나 결과 값에 통계적으로 유의한 차이가 존재하지 않음을 확인할 수 있었기 때문에 기존의 방법으로 산정할 수 없었던 V50에 대한 결과 값을 적용하는 것이 타당하다고 할 수 있다. Table 5를 살펴보면 시나리오 1 ~ 시나리오 6 모두 p-value가 0.05 이상으로 나타나 모두 통계적인 차이가 없음을 알 수 있으며, V50의 산출이 불가능할 경우 로지스틱 회귀분석을 사용하는 것이 타당함을 알 수 있었다.
5. 결 론
본 연구는 방탄성능 시험을 수행하는 과정에서 V50 산출이 불가능한 경우 이를 해결할 수 있는 방안에 대해 모색해보았다. 지금까지 V50을 산출하기 위해 다양한 변수와 방법론을 사용한 연구가 진행되어 왔지만 관련 연구들은 극소수였다. 그리하여 본 연구에서는 통계적 방법론을 적용하여 시험실무자가 쉽게 V50을 산출할 수 있는 방법을 제시하였다.
본 연구를 위해 시뮬레이션을 수행하였으며 다음의 가정을 설정하였다. 첫째, 해당 탄에 의한 해당 시료의 V50 값은 700 m/s이다. 둘째, 각 사격 후 탄속 700 m/s 이상에서는 완전관통, 이하에서는 부분관통이 발생하는데 이 과정에서 10%의 확률로 반대의 현상이 발생한다. 셋째, 해당 시료는 특정 탄속 이하에서는 100% 방호한다. 반대로 특정 탄속 이상에서도 100% 관통하게 되는데 여기에서 특정 탄속은 시나리오에 따라 %형태로 증감된다. 넷째, 탄속의 가감은 시나리오에 따라 % 형태로 증감된다. 다섯째, 계산 편의상 해당 시료에 대한 사격은 10회만 수행한다. 여섯째, 시편에 가해지는 탄자의 속성(무게, 형상 등)은 모두 동일하다.
시뮬레이션을 수행한 결과는 다음과 같다. 첫째, 대부분의 시나리오에서 기존의 방식과 개선된 방식으로 산출한 V50 값의 차이는 작게 나타났으며, 본 연구에서 가정한 V50 값에는 개선된 방식이 기존의 방식으로 산출한 V50 값보다 더 근접한 것을 알 수 있었다. 또한 결과 값에 대한 t검정 결과, 통계적으로 유의한 차이가 존재하지 않음을 확인할 수 있었기 때문에 기존의 방법으로 산정할 수 없었던 V50에 대한 결과 값을 적용하는 것이 타당하다고 할 수 있다. 탄속 범위의 차이에 따라 회귀식이 다르게 도출되었는데, 탄속 범위의 평균이 약 15 m/s 수준으로 작을 때에는 -0.32x(탄속) + 222.76으로 나타났으며, 탄속의 범위의 평균이 약 30 m/s 수준으로 클 때는 -0.21x(탄속) +146.7로 나타났다.
본 연구의 시사점 및 의의는 방탄성능시험을 수행하는 과정에서 발생하는 문제점을 통계적인 모형을 사용하여 사용이 용이하고 신뢰성 있는 방법론을 개발하였다는 점으로 본 연구 결과를 토대로 국내 방탄성능 시험에서 안정적으로 결과 값을 산출할 수 있도록 하는데 도움이 되고자 한다. 하지만 이러한 시사점에도 불구하고 향후 연구에서 보완해야할 한계점을 가지고 있다. 첫째, 실제 시험과정에서 발생할 수 있는 역전현상만을 고려하였을 뿐 다른 현상을 고려하지 못하였다. 둘째, 실증분석에 이용한 자료는 특정 탄에 대한 데이터만을 추출하여 사용하였다. 하지만 보다 정확한 분석을 위해서는 다양한 탄종과 다양한 시료를 가정하여 분석하는 것이 필요할 것이다. 향후 연구에서는 본 연구에서 제시한 방법론을 적용함에 있어서 탄종과 시료에 대한 범위를 확장한다면 좀 더 신뢰성 있는 결과가 나타나게 될 것이다.