1. 서 론
신제품의 개발과 관련된 공업실험이나 신약 개발과 관련된 제약회사에서의 연구 개발(R&D) 실험에서 엔지니어들이 결정해야할 첫번째 과제는 실험에 고려된 입력인자들의 수준들에 대한 랜덤화의 제약조건을 고려하여 실험 목적에 부합되는 합리적인 실험 계획을 제시하는 일이다. 그 다음으로 결정되어야 할 과제는 각각의 처리에서 실험의 반복의 크기를 결정하는 것이다. 또한, 초기단계의 실험에서 고려되어야 할 인자의 수는 많고 실험 실시에 비용이 많이 드는 경우에는 경제성을 고려하여 가능한 실험 조건의 일부에서만 실험을 실시하고, 효과들의 반정규확률그림에 의해 요인 효과의 크기가 원점을 지나는 선형 경향에서 벗어날 정도로 충분히 큰 효과를 핵심 효과로 선별한다. 선별된 핵심인자들에 대한 수준 변경의 경제성과 실험 환경의 동질성을 고려하여 결정된 요인배치법, 랜덤화 블록 계획법 혹은 분할법에서 실험의 반복의 크기는 일차적으로 반응 변수에 실제로 영향을 주는 핵심적인 입력변수들이 선별되어 모형에 포함되는 것을 통계적으로 보장할 수 있도록 결정되어야 한다. 각각의 실험에서 실험의 반복의 크기는 제1종 오류의 확률, 실용적으로 반응 변수에 충분한 영향을 준다고 판단될 수 있는 실험자가 검출하고 싶은 요인 효과의 오차에 대한 상대적인 크기(Signal-to-Noise ratio), 그 값에서의 제2종 오류의 확률에 따라서 결정된다.
기존의 소프트웨어 중 반복의 크기와 검정력을 산출할 수 있는 소프트웨어는 SAS, R, Minitab, Design Expert, Lenth Java applets 등이 있다. 그러나 SAS와 R, Minitab의 경우 분할법 실험에 대해서는 프로시저나 함수로 모듈화 되어있지 않아 분석자가 매크로 형태로 프로그래밍을 해야 한다. Design Expert와 Lenth의 Java applets은 분석자가 실용적인 실험계획법의 실험의 크기 결정에 쉽게 접근할 수 있으나 기능적인 측면에서 다소 부족함이 있다. Design Expert는 검출하고 싶은 요인 효과의 크기, 검정력, 반복의 크기 사이의 전체적인 관계도를 파악하기 어려우며, 제 1종 오류의 확률이 0.05인 경우에 대해서만 한정적으로 검정력을 구할 수 있다. Lenth의 Java applet은 Minitab에서 제공하는 그래프와는 다르게 한 그림에 하나의 반복에 대한 그래프를 표시하여 검출하고 싶은 요인 효과의 크기, 검정력, 반복의 크기를 동시에 비교하는 데에 어려움이 있다.
이 논문에서는 요인배치법, 랜덤화 블록 계획법과 분할법에서 제 1종 오류의 확률, 검출하고 싶은 요인 효과의 오차에 대한 상대적인 크기와 제2종 오류의 확률 β를 만족하는 실험의 반복의 크기를 결정하는 알고리즘을 설명하고, 엔지니어가 실용적으로 실험의 반복의 크기를 결정하는 것을 도와줄 수 있는 시각적인 방법인 그래프들를 제시하고, R을 통해서 구현한다.
2. 반복의 크기를 결정하는 알고리즘
각각의 실험에서 실험의 반복의 크기는 제 1종 오류의 확률, 실용적으로 반응 변수에 충분한 영향을 준다고 판단될 수 있는 실험자가 검출하고 싶은 요인 효과의 오차에 대한 상대적인 크기(Signal-to-Noise ratio), 그 값에서의 제2종 오류의 확률에 따라서 결정된다. 이를 위한 실험의 반복의 크기를 결정하는 알고리즘은 임용빈(1998)에서 제시된 방법을 이용한다. 이는 다음과 같다.
인자들의 각 수준조합에서 반복의 크기가 동일한 균형 실험계획법 모형에서 모수효과(fixed effects) A의 유의성 검정을 생각하자. F-검정 통계량의 분모에 해당되는 요인효과를 X로 표시하고, F-통계량의 자유도를 ν1, ν2, A의 수준 효과 αi들의 수준 간 산포 크기를 ϕ ( A ) = Σ α i 2 / ν 1 σ 2 X , E ( M S A )
인 비중심 F-분포의 분포함수에 의해 결정된다. (Tiku(1967), Marvin et al.(1970)) 자유도 ν1, ν2인 F-분포의 누적 확률이 1 - α되는 값을 F α (ν1,ν2 ) 로 표시할 때 유의수준 α 기각역은 {F : F ≥ Fα ν1,ν2 )} 이다. 대립가설이 참인 경우인 실험자가 검출하고 싶은 A의 수준 효과 산포크기 ϕ *(A)에서 비중심 모수의 값을 ∆*라 하자. ∆*에서 비중심 F-분포의 기각역에 속할 확률인 검정력이 적어도 1 - β 가 되도록 반복의 크기 r이 결정되어야 한다. 우선 F α (ν1,ν2 )에서의 비중심 F-분포함수 값이 β가 되는 비중심 모수의 값인 ∆ 를 찾는다. 검정력이 비중심 모수값의 단조 증가함수임을 주목할 때
를 만족하는 최초의 r이 반복의 크기이고, 검출하고 싶은 표준화된 주효과 A의 크기인
에서 검정력이 처음으로 1 - β보다 크게 된다. 즉,
를 만족하는 최초의 r을 구한다. 여기서 ∆ 는 R 프로그램의 “fpow” 패키지(package)에 있는 ncparamF 함수를 이용해서 찾을 수 있다. ncparamF는 α, β, ν1, ν2를 입력변수로 하여 비중심 모수의 값인 fλ 를 찾는 함수이다. 그런데 특히 주효과에 관심이 있을 때에 엔지니어들은 검출하고 싶은 주효과의 크기를 Δ *보다는 인자 A의 수준에서 모평균의 범위인
으로 표현하기가 쉽다고 생각한다. 이때 Δ *와 Δ1*의 관계는
임을 쉽게 보일 수 있다.
3. 효율적인 반복의 크기 결정을 위한 시각적 방법
반복의 크기는 실험 비용과 직결되기 때문에 분석자들은 되도록 적은 반복수를 결정하고자 하고, 실용적으로 검출하고 싶은 검출가능효과의 크기도 탄력적으로 결정한다. 반복의 크기와 최소검출가능효과의 크기를 기준으로 검출가능효과의 크기, 실험의 반복, 검정력 사이의 상호 관계를 파악하기 위한 그래프를 시각적으로 제안하여 효율적인 반복의 크기를 결정하려 한다.
최소검출가능효과의 크기와 검정력을 고려하여 반복의 크기를 결정하는 첫번째 시각적 방법으로 선택된 반복의 크기에서 최소검출가능효과의 크기와 검정력에 대한 그래프를 제안한다. 이 그래프에는 α, Δ*, β 조건을 만족한다고 추천된 반복의 크기가 4 이상이면 반복의 크기 r과 r-1, r-2에 대한 각 효과에서의 검출가능효과의 크기의 함수인 검정력 곡선이 나타난다. 연한 회색 점선은 검정력(power) 1 - β 를 만족할 때 검출가능효과의 크기를 찾기 위한 보조선이며, 진한 회색 점선은 각 효과가 검출가능효과의 크기 Δ *일 때의 검정력의 크기를 찾기 위한 보조선이다. 그래프의 오른쪽 아래에 범례를 통해 검정력이 1 - β 일 때 반복의 크기와 각 효과의 검출가능효과의 크기가 표시된다. 이 그래프를 통해서 각 효과의 검정력이 충분한 지를 시각적으로 확인할 수 있다.
두번째 시각적 방법으로 검정력이 고정된 상태에서, 반복의 크기와 최소검출가능효과의 크기에 대한 그래프를 제안한다. 특히 각 효과의 그래프를 겹쳐 그려 모든 효과를 동시에 고려한 반복의 크기를 결정하는 데에 효과적이다. 각 효과에 대해 다른 선으로 표현되며, 이는 범례를 통해 확인 가능하다. 회색 점선으로 주어진 검출가능효과의 크기 Δ *에 대응되는 반복의 크기를 찾을 수 있다.
세번째 시각적 방법으로 검출 하고 싶은 효과의 크기가 고정된 상태에서 반복의 크기와 검정력에 대한 그래프를 제안한다. 최소검출가능효과의 크기를 달리하며, 반복의 크기가 커짐에 따라서 각각의 효과의 검정력의 변화를 비교한다. 두개의 회색 점선은 검정력 1 - β 가 0.8, 0.9 일 때를 나타낸다. 검출가능효과의 크기에 따라서 반복의 크기와 검정력의 크기에 관한 정보를 얻을 수 있고 어떤 요인효과가 반복의 크기를 결정하는데에 가장 큰 영향을 미치는지 확인할 수 있다.
제시한 세 가지 그래프를 그리기 위해 R 프로그램을 사용하였으며 프로그램은 별도 요청 시 배부 가능하다.
4. 사례 분석
Hicks(1982)에 소개된 분할법 예제에 대해 랜덤화 블록설계와 분할법으로 실험했을 때의 반복의 크기 r에 관한 결과를 그래프를 통해서 비교해보자.
(예제) 전기 부품의 수명이 오븐 온도(Tj)와 굽는 시간(Bk)에 영향을 받는지 알고 싶다. 온도 ( °F)는 580, 660, 620, 640의 네 수준으로 선택되어졌고 시간은 5분, 10분, 15분의 세 수준이 선택되어졌다. 오븐 온도의 선택에 비용이 많이 들기 때문에 오븐 온도를 먼저 랜덤하게 결정한 후 세 개의 전기 부품을 이 온도에서 랜덤하게 선택된 시간의 순서로 차례차례 굽는다. 랜덤하게 선택된 온도에서 실험을 모두 실시한 후, 이 전체의 절차를 반복(Ri)하는 분할법(split plot design)을 실시한다. α=0.01, ∆*=1.5에서 온도 효과와 시간 효과, 온도와 시간의 교호작용효과에 대한 검정력이 모두 최소한 1 - β = 0.8이 되도록 반복의 크기를 결정하라.
Table 1은 위의 예제를 랜덤화 블록설계와 분할법으로 실험했을 때 2절의 알고리즘을 이용해서 나온 결과를 정리한 것이다. 이를 보면 분할법 시행시 실험 반복의 크기가 5로 랜덤화 블록설계로 시행했을 경우의 반복의 크기 3보다 커졌음에도 주구(whole plot)에 배치된 오븐온도(인자 T) 요인의 최소검출가능효과의 크기가 더 커져 랜덤화 블록설계보다 정밀하게 검출하지 못한다. 즉, 랜덤화 블록설계 대신 분할법을 이용하면 오븐 온도(T)를 자주 바꾸지 않아도 된다는 편의성이 있지만 반복의 크기가 5임에도 랜덤화 블록설계에 비해 주효과 T에 대한 검정력이 떨어진다.
랜덤화 블록설계와 분할법에 대한 검출하고 싶은 효과의 크기에서 검정력을 보장하는 실험의 크기 결정을 위해서 3절에서 제안한 세 개의 그래프를 이용하여 분석하고자 한다.
4.1 최소검출가능효과의 크기 대(vs) 검정력
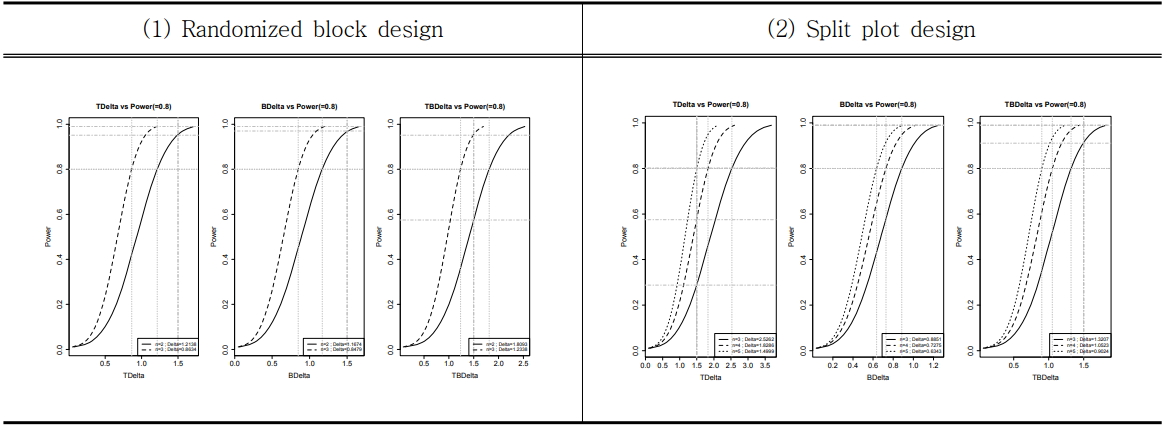
Figure 1은 Table 1에 주어진 r을 기준으로 Δ와 1 - β 사이의 관계를 나타낸 그림이다. 각 요인의 최소검출가능효과의 크기가 증가할수록 검정력이 증가함을 알 수 있다. 랜덤화 블록설계의 경우 반복 3회만에 최소검출가능효과의 크기에서의 검정력이 기준을 만족하므로 r이 3과 2일 때 그래프를 나타낸다. 분할법은 최소검출가능효과의 크기가 5이므로 r이 5, 4, 3일 때의 그래프를 나타낸다. 랜덤화 블록설계의 반복의 크기인 r=2일 때의 그래프를 보면, 주효과 T와 B는 .9 이상의 충분한 검정력을 갖지만, 교호작용효과 TxB 의 검정력은 0.6 미만으로 충분하지 않음을 알 수 있다. 여기서 랜덤화 블록설계의 축차적인 실험 실시가 가능하다고 하자. 반복의 크기 2로 실험을 실시하고 실험자료를 분석하면, 교호작용효과 TxB 의 p-값을 근거로 추가 실험 여부를 축차적으로 결정할 수 있다. 반복의 크기, 즉 블록의 갯수가 2인 경우에 실험자료의 분석을 통해서 교호작용효과 TxB의 p-값이 0.25 이상으로 유의하지 않은 경우, TxB 효과는 무시할 수 있고, Δ * =1.5에서의 주효과 T와 B의 검정력은 0.9 이상으로 블록의 크기 2로 충분한 검정력을 갖기에 이 그림을 활용하여 반복의 크기를 2로 정할 수 있다.
또한 Figure 1을 통해 분할법으로 시행했을 때의 효과가 주구에 배치된 효과인가 분할구(split plot)에 배치된 효과인가에 따라서 검정력의 차이가 많이 남을 확인할 수 있다. 분할구 그래프의 진한 회색 점선을 보면 r이 3, 4, 5에서 각 효과의 최소검출효과의 크기가 1.5일 때 검정력의 차이를 보여준다. 이를 보면 주구에 배치된 온도 효과(T)가 분할구에 배치된 시간효과(B), 온도와 시간의 교호작용효과 TxB 보다 검정력이 크게 떨어진다. 예를 들면, r이 3일 때 주구에 배치된 온도효과 T의 경우 검정력이 0.3 미만이지만, 분할구에 배치된 TxB 효과의 검정력은 0.9 이상으로 충분한 검정력을 갖고 있다. 그래프의 범례를 보면 분할법으로 실험의 크기를 3으로 하면, 검정력 0.8에서 T, B, TxB에 대한 최소검출가능효과값은 2.5262, 0.8851, 1.3207이다. 이를 통해 랜덤화 블록설계로 실험을 3회 실시하였을 때보다 주효과 T의 최소검출가능효과의 크기가 크게 증가하여 주구에 배치된 효과의 정밀한 검출이 어렵다는 것을 알 수 있다.
4.2 반복의 크기 대(vs) 최소검출가능효과의 크기
Figure 2는 주어진 검정력에서의 반복의 크기와 최소 검출 가능 효과의 크기에 대한 그래프를 보여준다. 이 그래프를 통해서 최소 검출 가능 효과의 크기인 Δ *값이 달라진 경우에, 즉 1.5에서 1로 달라진 경우에 그에 맞는 반복의 크기를 쉽게 파악할 수 있다. 또한, 랜덤화 블록설계를 보면 TxB 효과에 대한 그래프가 가장 위에 있어 주어진 반복의 크기에서 검출할 수 있는 최소 검출 가능 효과의 크기인 Δ *값이 TxB 효과가 가장 커서, 실험의 크기를 결정하는데에 TxB 효과가 가장 큰 영향을 미침을 알 수 있다. Figure 1에서 설명한 것과 같이 랜덤화 블록설계의 축차적인 실험 실시를 통해서 교호작용효과 TxB가 유의하지 않은 경우 블록의 갯수 2에서 검정력 0.8을 갖는 T, B 효과의 Δ * 의 값은 1.5 미만으로 이 그림을 활용하여서도 반복의 크기를 2로 줄일 수 있다. Figure 2의 분할법 그래프를 보면 주구에 배치된 T효과에 대한 그래프가 가장 위에 있어 반복의 크기를 정하는 데에 가장 큰 영향을 미침을 알 수 있다. 즉, 실험의 크기는 T의 검출 가능 효과의 크기에 따라 결정됨을 확인할 수 있다.
4.3 반복의 크기 대(vs) 검정력
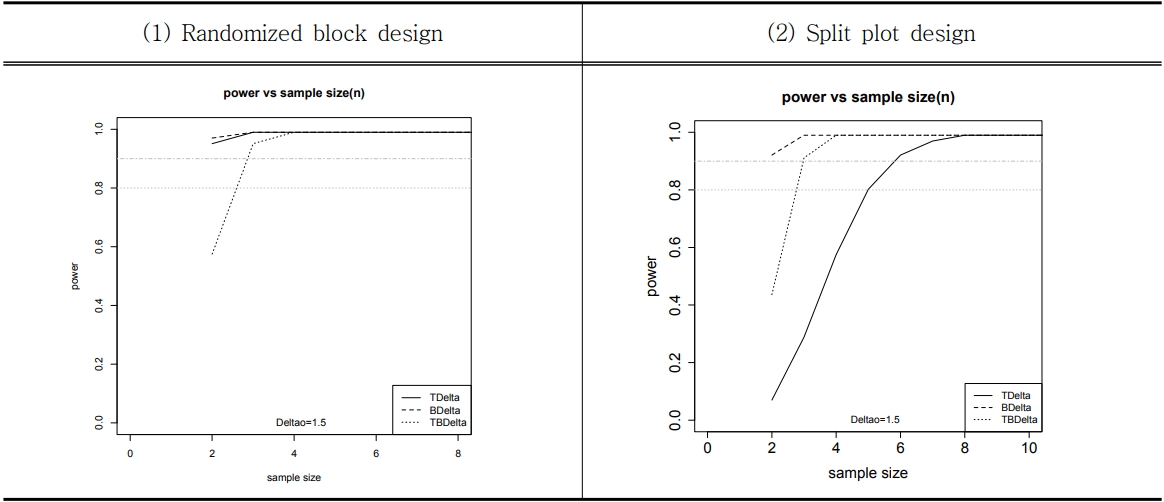
Figure 3은 주어진 최소 검출 가능 효과의 크기인 Δ *가 1.5일 때 주효과 T와 B, 교호작용효과 TxB에 대해 반복의 크기에 따른 각각의 요인효과의 검정력을 동시에 확인하는 그래프이다. 주어진 반복의 크기에서 검정력이 가장 낮은 효과의 검정력 값에 따라서 반복의 크기가 결정된다. 랜덤화 블록설계에서 검정력의 그래프가 가장 아래에 위치한 효과는 TxB 효과이다. 반복의 크기 2에서 주효과 T와 B의 검정력은 0.9 이상이지만, TxB 효과의 검정력은 0.6 미만이다. 반복의 크기 3에서 주효과 T와 B의 검정력은 1에 가깝고, TxB 효과의 검정력은 0.9 이상임을 알 수 있다.
분할법에서 검정력의 그래프가 가장 아래에 위치한 효과는 주구에 배치된 T효과이고, 그 위에 위치한 효과가 분할구에 배치된 TxB 효과이고, 가장 위에 있는 효과가 B이다, 따라서 T효과의 최소검출효과의 크기인 Δ *에 따라서 반복의 크기가 결정된다. Δ *가 1.5인 경우 반복의 크기 5에서 주구에 배치된 T 효과의 검정력이 0.8 이상이다. 반복의 크기가 5인 경우에 분할구에 배치된 효과들의 검정력은 1에 가까운 값을 갖는다.
5. 결 론
본 논문은 R 프로그램을 활용하여 실용적인 실험계획법인 요인배치법, 랜덤화 블록계획법과 분할법에서 제 1종 오류의 확률 α , 검출하고 싶은 효과의 크기에서 검정력을 만족하는 실험 반복의 크기를 제시하였다. 또한 분석자가 실용적으로 반복의 수를 결정하는데 도움이 되기 위한 시각적인 방법으로 결정된 실험의 반복의 크기를 기준으로 검정력, 최소검출가능효과, 반복의 크기 사이의 상호 관계를 파악할 수 있는 세가지 그래프 방법을 제시하였다, 분석자는 이 그래프들을 통해 반복의 수를 줄일 수 있는 방안을 강구 할 수 있으며, 이는 실험의 비용을 줄이는데 직접적인 영향을 줄 수 있을 것이다.