1. 서 론
국내에서 신용카드는 점점 더 널리 이용되고 있다. 금융감독원에 따르면 2017년 말 기준 신용카드 발급매수는 9천 946만 매로 2016년 대비 382만 매(4%) 증가했다(FSS, 2018). 또한 2017년 신용카드 이용액은 사상 처음으로 600조 원을 넘어(627조 3천억 원) 2016년 대비 5.3% 증가했다. 여신금융협회에 따르면 민간소비지출에서 신용카드의 이용 비중은 71.9%에 달하였다(CREFIA, 2017). 이것은 신용카드가 소비지출의 71.9%를 차지함으로써 현금을 제치고 가장 보편적인 결제 수단으로 이용되고 있음을 의미한다.
그런데 이런 양적 팽창에도 불구하고 카드사들의 순이익은 계속 감소하는 추세이다. 금융감독원에 따르면 지난해 8개 전업카드사의 순이익은 전년 대비 32.3% 감소했다(FSS, 2018). 카드사들의 순이익은 2014년 2조 2천억 원을 정점으로 2015년 2조원, 2016년 1조 8천억 원, 2017년 1조 2천억 원으로 3년 연속 감소하고 있다. 금융감독원은 그 원인으로 (1) 낮은 가맹점 수수료율 적용 대상인 영세 중소 가맹점의 확대 (2) 부가서비스 등 마케팅 비용의 증가 (3) 충당금 적립 기준 강화에 따른 대손 비용 증가를 들고 있다.
이것은 신용카드의 수익을 결정하는 주요한 요인 중 하나가 부가서비스 비용임을 시사한다. 부가서비스는 다양한 의미로 사용되며 주로 카드 이용에 따른 할인, 포인트 적립, 마일리지 적립 등의 혜택을 의미한다. 가맹점 수수료율이나 충당금은 정책에 의해 결정되는 반면 부가서비스는 카드사가 조절할 수 있는 요인이다. 따라서 정확한 부가서비스 비용 예측이 가능하다면 손익 관리에 큰 도움이 될 것이다.
부가서비스는 카드 사용자들에게 인지되는 서비스 품질의 중요한 요소이기도 하다. KDI의 설문조사에 따르면 76%의 소비자들이 신규로 신용카드를 개설할 때 부가서비스 혜택을 고려한다고 답변했다(Cho and Lee, 2014). 또한 신용카드의 일반적인 이용목적에서도 부가서비스 혜택이 가장 큰 요인이며 신용카드 관련 피해 인식도 포인트, 마일리지 적립 등 부가서비스 관련 항목이 상위를 차지했다(Jung et al., 2015). 이처럼 부가서비스는 수익 관점에서도, 서비스 품질 관점에서도 신용카드의 상품력을 결정하는 중요한 요소임을 알 수 있다.
그러나 부가서비스 비용율(이하 부가서비스 요율), 특히 신규 카드 출시 시점의 부가서비스 요율을 예측하는 데 있어 신뢰할 만한 분석 방법론은 아직까지 구축되지 못한 것 같다. 금융감독원의 규정에 따르면 새로 출시되는 신용카드의 부가서비스는 3년간 유지해야 한다(Kang 2018). 3년이 지나면 6개월의 사전 공지 기간을 거쳐 서비스 내용을 바꿀 수 있는데, 2013 ~ 2017년 6월 사이에 중단되거나 축소된 부가서비스는 372건이고 이에 연관되는 카드는 4,047종에 이르렀다(Kim 2017).
심지어 부가서비스 비용이 과도하게 발생하여 카드 상품 자체가 없어진 경우도 있다. 최근의 사례로는 출시 6개월만에 단종된 S카드(2016)가 있었고 그 전에는 H카드(2013)가 유명한 단종 사례였다(Park 2017). 어느 인터넷 블로거는 과거에 존재했던 신용카드 20종의 혜택과 단종 원인을 상세히 열거하면서 지나친 부가서비스 혜택과 그로 인한 과도한 비용이 신용카드 단종의 원인임을 지적하기도 했다(Aedi 2017).
부가서비스의 축소와 폐지 사례 중 일부는 카드사의 공격적인 마케팅으로 볼 수도 있겠지만, 카드상품의 단종까지 공격적인 마케팅으로 보기는 힘들다. 이것은 부가서비스 비용의 예측이 치밀하지 못 했기 때문에 발생한 사건이라고 봐야 한다. 부가서비스 비용은 사용자들의 이용행태에 밀접하게 연관되어 있는데, 그것을 정확하게 예측하고 카드를 만들었다면 이렇게까지 많은 부가서비스 중단 및 축소 사태는 없었을 것이다.
그러나 부가서비스 요율 예측의 기반이 되는 신용카드 이용행태에 관한 연구는 상당히 제한적인 범위에서만 이뤄져 왔다. 이런 현상은 국내·외 구분 없이 공통적인데, 그 이유는 이용행태에 관한 자료가 제한적으로만 공개되기 때문이다. 또 하나의 이유는 카드사들이 확률분포 보다는 데이터마이닝 기법에 주로 의존하기 때문이다. 데이터마이닝은 거대한 모집단의 행태가 안정화된 상태에서 발생하는 새로운 객체의 속성을 분류(classification)하는 데는 탁월하지만 모집단 전체의 행태 변화를 묘사하고 예측(prediction)하는 데는 알맞지 않거나 비효율적인 경우가 있다.
이에 따라 본 논문은 신뢰할 만한 신용카드 부가서비스 요율 예측 모형을 구축하는 것을 목적으로 모형을 수립하는 데 따르는 쟁점들을 소개하고, 이를 바탕으로 신용카드 부가서비스 요율 예측 모형을 제시하고자 한다. 2장에서는 부가서비스 요율의 개념과 범위에 관한 설명이 제시된다. 3장에서는 예측 모형을 구축하는 데 필요한 주요 요소와 가정을 열거한다. 4장에서는 부가서비스 요율 예측 모형을 상술하고 활용 방법을 소개한다. 마지막으로 5장에서는 구축된 모형의 효용과 후속 연구 방향에 대하여 기술한다.
2. 부가서비스 요율의 개념
2.1. 부가서비스의 종류
신용카드 부가서비스는 사전적인 의미보다는 주로 혜택(benefit) 또는 가치제안(value proposition)이라고 불리며 그밖에도 상황에 따라 다양한 명칭으로 불린다. 대체로 카드 사용에 따른 할인이나 적립 등 즉각적인 보상을 지칭한다. 한편 카드사용자의 입장에서는 연회비 혜택, 금리 우대 등 금전적인 이익이 수반되는 모든 서비스가 부가서비스로 인식된다. 일반적으로 신용카드 부가서비스라고 인식되는 혜택들을 구분하여 열거하면 <Table 1>과 같다.
부가서비스 중 가장 기본적인 것은 신용카드에 내장되어 사용처(가맹점)에서 카드를 이용할 때마다 제공되는 할인(discount)이나 포인트 적립(reward) 등의 서비스이다. 그 다음 놀이공원 할인, 공항 라운지 이용권, 발레 파킹 등 대개 연간 이용횟수가 정해진 서비스들이 있다. 이들은 신용카드의 고유한 부가서비스라기 보다는 일종의 멤버쉽 서비스이다. 그 다음 이와 비슷한 유형으로 신용카드 제휴 가맹점들이 제공하는 할인 및 적립 서비스가 있다. 백화점이나 대형마트에서 특정 카드 사용자에게만 상시 제공하는 할인 서비스 등이 해당한다.
카드사에서 비정기적으로 시행하는 프로모션도 부가서비스의 일종으로 간주되기도 한다. 주로 일정 기간 동안 특정 카드로 특정 한도 이상의 금액을 사용하면 제공되는 조건부 할인이나 적립 혜택이다. 마지막으로 연회비 지원, 무이자할부, 금리 우대 등은 사용자의 입장에서는 부가서비스의 일종이지만 카드 거래와 직접적인 관계가 없으므로 엄밀하게는 부가서비스의 영역이 아니다.
2.2. 부가서비스 요율
부가서비스 비용의 수준을 나타내는 지표로는 부가서비스 요율이 사용된다. 이것은 신용카드 이용금액에서 부가서비스 비용이 차지하는 비중을 의미한다. 앞서 밝힌 대로, 부가서비스 요율은 수익 관리의 중요한 항목이자 서비스 품질의 지표이므로 카드사의 주요 KPI 중 하나이다. 한국은행 자료에 따르면(BOK, 2012) 2011년 한 해 전업 카드 5개사의 연간 부가서비스 요율은 0.7% 수준이었다. BC카드에서 발간되는 ‘비씨통계’(BC, 2016)에서도 전업 카드사들의 부가서비스 요율은 매년 0.7% 전후로 집계되어 일정한 편이었다.
전체 비용에서 부가서비스 비용은 매우 큰 비중을 차지한다. 2015년의 경우 전업 카드사 8개의 총 부가서비스 비용은 2조 7천 7백억 원으로 회원 모집 비용이나(9천 8백억 원), 타겟/매스 마케팅 비용(6천 7백억 원)에 비해 월등히 높았다. 따라서 부가서비스는 카드사의 손익을 결정하는 가장 중요한 비용 요소임을 알 수 있다.
부가서비스의 수준을 나타내는 KPI로 부가서비스 요율이 사용되는 관행은 요율 예측 모형 구축에 유리한 조건이다. 복잡한 지표가 사용된다면 그만큼 상세한 자료가 필요할 것이다. 그런데 전체 사용금액(일시불+할부) 대비 서비스 비용의 비율만 나타내면 되므로 사용금액과 부가서비스 비용의 절대금액 수준과 상관없이 상호 관계만 정확히 파악하면 되는 것이다.
2.3. 부가서비스의 제공 방법
부가서비스는 다양한 형태로 제공된다. 할인(현장할인, 청구할인), 포인트 적립, 캐시백, 항공 마일리지 적립이 대표적인 유형이다. 신용카드를 발급하자마자 제공되는 바우처나 할인 쿠폰 등도 있지만 그런 서비스들은 별도의 마케팅 비용으로 처리하는 것이 일반적이므로 포인트, 할인, 캐시백, 마일리지 등 4가지 유형만 있다고 가정해도 문제는 없다.
2.4. 모형 구축에 적용되는 부가서비스의 범위
지금까지 부가서비스의 여러 가지 특징들을 살펴보았다. 이로부터 본 논문의 연구 대상과 범위는 다음과 같이 정하고자 한다. 첫째, 개인 신용카드의 이용행태만을 대상으로 한다. 이것은 자연발생적인 신용카드 거래만을 대상으로 한다는 의미이다. 법인카드까지 포함하면 계약에 의한 사용, 특정 업종 편향 등 인위적인 이용행태가 포함되게 된다.
둘째, 2.1의 <Table 1>의 세부 항목 중 카드 탑재 서비스(embedded service)만을 연구 대상으로 한정한다. 즉, 가맹점 이용거래에 연관된 부가서비스만을 대상으로 삼는다는 뜻이다. 이 항목은 전체 부가서비스 중 가장 큰 비중을 차지하며, 카드 사용자의 일상적인 소비 행태에 밀접하게 연관된다.
셋째, 2.3에 제시한 4가지 유형 중에서 할인서비스만을 대상으로 한다. 그 이유는 대개의 경우 포인트나 캐시백, 마일리지는 1단위가 1원이 아니기 때문이다. 2010년대 초까지만 해도 포인트 소진율은 중요한 쟁점이었다(Park 2011). 지금은 포인트 유효기간 폐지 움직임 등으로 인해 소진율이 거의 100%에 달하므로 예전만큼 큰 이슈가 되지는 않지만, 카드사별로 포인트 1점의 단가는 다를 수 있다. 이같은 문제는 캐시백에도 동일하게 적용된다. 항공 마일리지 카드 역시 1마일당 단가가 카드사별 제휴 항공사별로 일정하지 않으므로 요율 산정에 어려움이 있다. 그러나 할인서비스는 원 단위이기 때문에 부가서비스 비용과 그에 따른 요율을 정확하게 계산할 수 있다.
2.5. 부가서비스 요율 예측의 의의
앞서 부가서비스 축소와 카드 단종 사례를 통해 밝혔듯 정확한 부가서비스 요율 예측은 매우 중요한 일이다. 여기서 명확히 해야 할 점은 본 연구의 대상은 특정 카드를 이용하는 사용자 집단 전체의 요율이며 신용카드 상품이 출시되기 전 사전 분석이라는 사실이다. 신용카드 이용 자료는 카드 뿐 아니라 가맹점이나 특정 사용자 집단, 예를 들어 ‘서울 마포구 거주 신용카드 사용자’ 등 여러 가지 축으로 수집될 수 있는데 여기서는 단일 카드를 사용하는 사용자 집단의 이용행태가 분석 대상이다. 또한 신용카드가 출시된 후에는 부가서비스 요율을 집계하면 되지 예측할 필요는 없으므로 본 연구의 대상은 신규 카드의 출시 전 사전 분석이다.
<Table 2>에 제시된 전업 카드사들의 평균 부가서비스 요율은 0.7% 수준이었다. 카드사들이 감당할 수 있는 요율은 이보다 다소 높을 것으로 추정된다. 현재 조건 없는 혜택을 제공하는 카드들 중에는 0.8% 할인을 제공하는 카드도 있다(Park 2018). 부가서비스 비용은 카드사별로, 카드별로, 또 가맹점과의 제휴 관계별로 차이가 있을 수 있으나, 조건 없는 혜택 제공 카드들의 요율이 이 정도라면 부가서비스 요율의 고/저 기준은 1% 정도로 보면 충분할 것으로 여겨진다. 즉, 신용카드의 요율이 1% 이상이면 높고 그 미만이면 적정하다고 판단할 수 있다. 이 수치는 제휴사 분담 비용을 뺀, 순수하게 카드사가 지불하는 비용 기준이다. Park(2017)은 요율이 2% 이상일 때 고혜택 카드라고 분류했는데 소비자 입장의 요율이므로 제휴사 비용도 포함된 요율로 보인다.
본 연구에서 분석 대상으로 삼는 카드들은 각 회사가 추천하는 인기 상품이므로 상대적으로 높은 부가서비스 요율을 나타내는 것이 당연하다. 부가서비스 요율 예측 모형의 주요 용도는 지나치게 높은 요율을 가질 위험이 있는 카드를 판별하는 것이다. 요율의 예측은 새 카드의 출시 전에 이루어지는데, 사전에 사용자 집단의 이용행태가 어떻게 형성될지 정확히 예측하기는 매우 힘들다. 따라서 예측 모형의 결과물로는 실무적으로 적용 가능한 요율의 상한과 하한을 산출하는 것이 바람직하며, 데이터마이닝 보다는 확률분포에 의거한 방법론이 더 알맞다고 판단된다. 왜냐하면 확률분포 모형은 몇 개의 파라미터 값을 변경하는 것으로 전체 집단의 행동 변화를 묘사할 수 있기 때문이다.
3. 부가서비스 요율 예측 모형의 주요 요소
3.1. 신용카드와 부가서비스에 관한 연구
신용카드의 이용행태에 관련된 연구는 카드의 결제 기능에 대한 제한적 인식과 공개 자료의 부족 등으로 인해 활발하게 이뤄지지는 못 했다. Schmittlein et al.(1987)은 일반적인 고객 계수 모형을 수립하면서 거래의 발생을 포아송 프로세스로 가정하였다. Till and Hand(2003)는 1996년 한 해 동안 어느 주유소에서 2,159명의 신용카드 사용자가 일으킨 40,068건의 거래 자료를 바탕으로 거래 빈도가 음의 이항분포를 따른다고 제안하였다. 그러나 음의 이항분포는 포아송 프로세스의 지수분포와 큰 차이가 없는 형태로서, 신용카드의 이용행태만이 갖는 새로운 분포를 제안했다고 보기는 어렵다. 또한 연구에 사용한 자료는 주유소라는 가맹점을 축으로 수집된 것이므로 일반적으로 단일카드 사용자들이 발생시키는 이용행태와는 차이가 있을 수밖에 없다.
신용카드 이용금액에 관한 분포는 Fan(2016)이 중국의 한 신용카드 회사의 44개월치 자료를 이용하여 제안하였는데, 로그정규분포를 가정하였다. 이 때 신용카드 거래의 발생은 음의 이항분포가 아니라 포아송 프로세스의 지수분포로써 적합하였다. 이 모형에 따라 신용카드 거래데이터를 생성하면 일정 기간 동안 누적된 카드 이용금액별 사용자 수는 지수분포와 같은 우하향 분포를 따르게 된다. Lee and Roh(2018)는 서울시 빅데이터 캠퍼스에서 제공하는 실제 자료 등을 이용하여 국내 신용카드 데이터도 이와 유사한 분포를 따름을 보였다.
국내 신용카드 부가서비스에 관한 연구는 서론에서 소개한 바와 같이 카드 사용자들의 부가서비스 선호도가 높다는 사실을 밝힌 수준에 머물러 있다. 그밖에 부가서비스 효용을 향상시킬 수 있는 상품 개발 제안(An et al. 2015)이나 어플리케이션 제안(Jung et al. 2015) 등으로 발전해 왔다. 하지만 부가서비스의 수준을 계량화하려는 시도는 없었다. 이런 상황에서 본 연구는 카드 사용자들의 이용행태를 확률분포로 묘사하고, 그것을 통해 부가서비스의 수준을 부가서비스 요율이라는 계량적 지표로서 제시하고자 한다.
3.2. 브랜드검색 결과와 주요 신용카드
부가서비스 요율 예측 모형을 구축하기 위해서는 연구 대상 신용카드를 선정해야 한다. 현재 시점에서 신청가능한 수 천 종의 카드를 전부 분석의 대상으로 선정하는 것은 불가능하고, 또 그럴 필요도 없다. 왜냐하면 이들 중 대부분은 더 이상 별다른 혜택을 받을 수 없는 카드들이기 때문이다. 가맹점 프랜차이즈의 생성과 소멸이 매우 잦은 상황에서는 흔히 발생하는 현상이다.
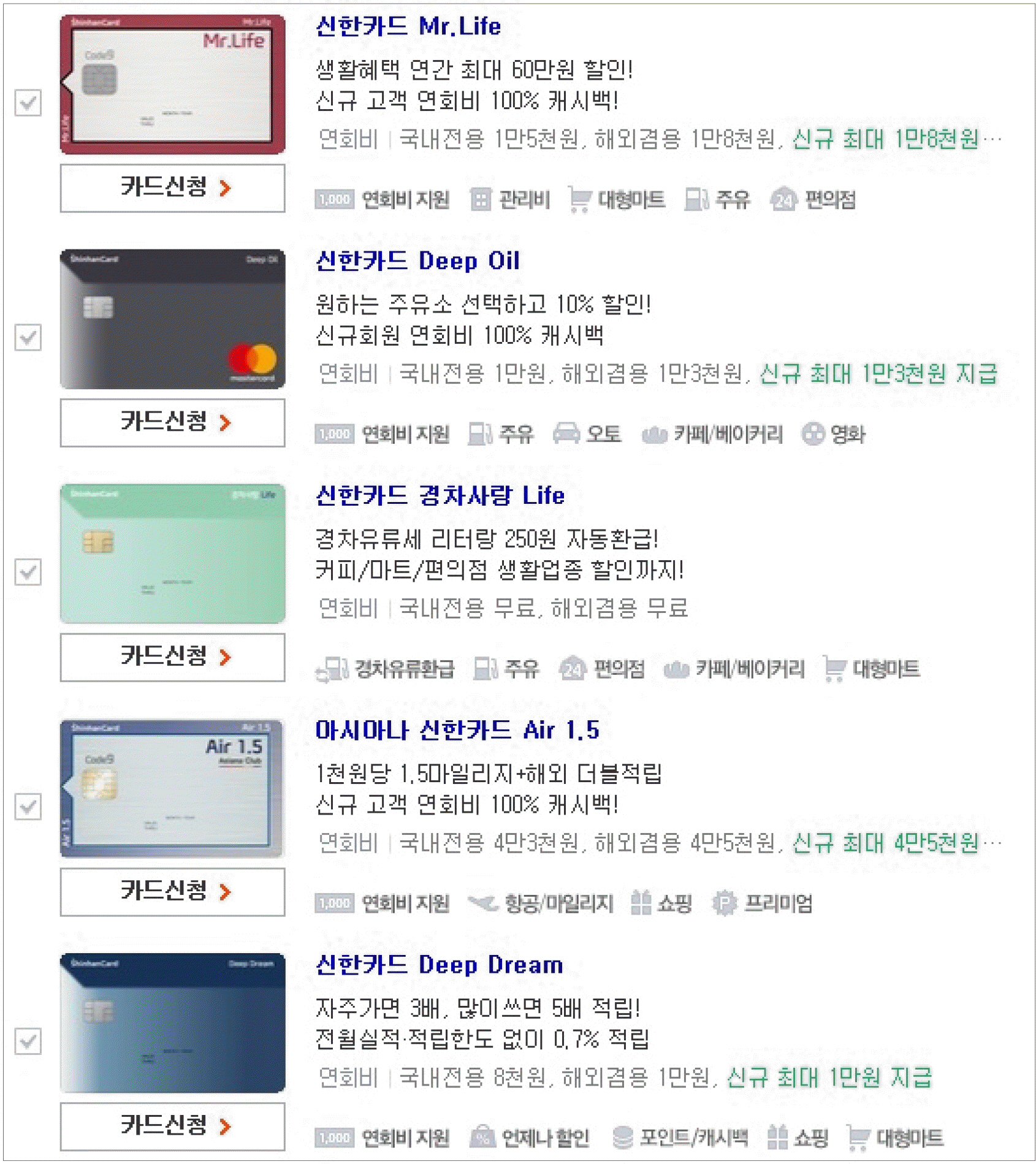
따라서 현재 가장 인기 있는 카드들을 분석 대상으로 삼는 것이 바람직한데, 네이버의 ‘브랜드검색’ 기능을 이용하면 각 사별로 가장 활발하게 추천하는 카드들을 찾아 볼 수 있다. 가령 네이버에서 ‘신한카드’라는 키워드를 입력하면 <Figure 1>과 같은 화면이 나타난다. 이것은 신한카드가 네이버를 통해 추천하는 카드들로서 회사가 소비자들에게 가장 어필하고 싶은 카드이다.
금융감독원 금융통계정보시스템(http://fisis.fss.or.kr/fss)에 따르면 2017년 한 해 동안 8개 전업 카드사 중 상위 5개사(신한, 삼성, 현대, KB, 롯데)가 시장점유율 10% 이상을 달성했고 이들 5개사의 점유율 합은 83%에 달했다. 따라서 이 5개사의 브랜드 검색 결과로 나타난 25종의 카드는 현재 가장 추천 지수가 높은 ‘주요 신용카드’라고 할 수 있다. 본 연구에서는 2018년 8월 1일부터 10일까지 열흘간 브랜드 검색을 한 결과 25종의 카드를 선정했고 그들을 부가서비스의 유형별로 분류한 결과는 <Table 3>과 같다.
전체 25종의 카드 중 17종이 할인형 카드였다. 이 가운데는 할인과 적립이 섞인 형태도 있었지만 순수하게 할인혜택만 주는 카드가 대부분(17종 중 14종)이었다. 신용카드 광고는 언제나 다양한 라이프 스타일에 특화된 카드라는 점을 홍보하지만 부가서비스의 특별 혜택 가맹점을 살펴 본 결과 사용자가 실제로 체감할 수 있을 만큼 사용처가 특화된 카드는 주유카드와 항공카드 뿐이었다. 다른 카드들은 혜택 가맹점들이 유사하여 ‘일반 소비형 카드’로 통칭할 수 있는 수준이었다.
이 분류가 의미하는 바는 다음과 같다. 우선 이들은 모두 개인용 카드이다. 그리고 할인형 카드가 대부분이다. 이것은 2.4에서 선정한 예측 모형 구축에 적용되는 부가서비스의 조건과 일치하는 특성들이다. 또한 이들 25종의 카드에 탑재된 부가서비스를 분석한 결과 신용카드 사용에 따른 혜택이 대종을 이루었고 사용금액에 비례하여 혜택이 커지는 구조였다. 다만 25종 중 2종(할인형 1종, 포인트 적립형 1종)은 이용금액이 아닌 이용 횟수 당 한도를 적용하거나 포인트 적립시 가변 적립율을 적용하여 쉽게 비례관계를 적용할 수가 없었다.
그러나 대부분의 카드들은 2.4에 제시한 조건들을 잘 따르고 있으며, 그에 따라 부가서비스 요율 예측 모형 수립을 위해 제시한 2.4의 3가지 조건들은 현실과 잘 맞는 가정이라고 할 수 있다.
3.3. 부가서비스 요율 예측 모형의 주요 요소
브랜드 검색을 통해 수집한 25종 카드의 부가서비스 내역과 제공방식을 상세히 관찰한 결과 <Table 4>와 같은 공통 요소들이 있음을 도출하였다. 이 공통 요소들로부터 크게 동떨어진 혜택을 제공하는 카드는 없으므로 공통 요소들을 적용하여 부가서비스 요율을 계산하는 예측 모형을 만들면 그것을 곧 표준화 모형으로 볼 수 있다.
25종의 카드 대부분에 걸쳐 공통적으로 나타나는 부가서비스 혜택은 특별할인 대상 가맹점에서 사용한 금액에 대해서는 특별할인율을 적용하고, 할인금액의 상한이 넘는 금액과 일반할인 대상 가맹점 사용금액에 대해서는 일반할인율을 적용하는 것이다. 그리고 특별할인율과 할인금액의 상한은 전월실적에 따라 사용자별로 차등적으로 결정된다.
이밖에도 무이자할부 이용금액에는 할인을 적용하지 않거나, 연간 실적이 일정 금액을 넘으면 추가 혜택(주로 포인트 적립)을 주거나 이용금액의 단가가 특정 하한을 넘어야 할인을 받을 수 있는 등의 세부 내역도 있었다. 그러나 이런 조건들은 <Table 4>에 열거된 5가지 공통 요소에 비하면 아주 작은 부분이므로, 예측 모형은 이 5가지 공통 요소들만 포함하면 충분하다고 판단된다.
3.4. 업종별 신용카드 사용금액의 특성
한국은행 경제통계시스템(http://ecos.bok.or.kr/)의 지역별 소비유형별 신용카드 실적을 조회하면 업종별 신용카드 실적을 볼 수 있다. <Table 5>는 2017년 4분기의 월별 업종별 신용카드 실적이다. 이 자료에서 알 수 있는 것은 신용카드 실적이 월별로 매우 일정하다는 사실이다. 한국은행 자료를 이용하여 신용판매(일시불+할부) 이용금액 기준으로 2017년 한 해 동안의 월별 계절지수(당월 이용금액/월 평균 이용금액)를 계산하면 영업일수가 적은 2월을 제외한 나머지 11개월은 최대 1.06(12월)부터 최소 0.96(1월)까지 분포하여 큰 차이가 없었다. 같은 맥락으로 업종별 사용실적도 월별로 매우 일정하게 유지되었다.
자료를 보면 공식 집계 업종만 해도 매우 다양하며, 신용카드에서 혜택을 제공하는 업종은 그중 일부에 불과함을 알 수 있다. <Table 5>의 두 번째 칼럼은 25종의 카드 중 ‘일반 소비형’ 그룹의 카드들이 주로 혜택을 제공하는 업종을 표시한 것인데 이들의 실적을 합하면 전체 사용금액의 45% 정도이다. 그러나 실제로 특별할인율이 적용되는 업종은 이보다 훨씬 적다. 예를 들어 전자상거래/통신판매 전체가 아니라 특정 온라인 쇼핑몰에서 사용한 금액에 대해서만 특별할인율이 적용되기 때문이다. 따라서 특별 할인 혜택의 적용을 받는 이용금액의 전체 이용금액 대비 비중은 최대 30% 정도로 여겨진다. 카드사들도 특별 할인 적용을 받는 이용금액이 커지는 것을 원할 리 없으므로 혜택 가맹점의 규모를 조절한다. 이로부터 부가서비스 요율 예측 모형에 연관된 중요한 특징이 추가적으로 도출된다.
(가정 1) 전체 사용금액 및 특별할인율 적용 업종에서의 이용금액은 월별로 일정하다
(가정 2) 전체 사용금액과 특별할인율 적용 업종 이용금액의 비율은 월별로 일정하다
따라서 요율 예측 모형은 기간별 시기별로 차별화 할 필요 없이 어느 특정 한 달의 행태를 묘사하는 것으로 충분하다. 이것은 모형이 구축되었을 때 활용 가능성과 효용을 크게 높여주는 속성이다.
매월 업종별 이용금액이 일정한 특징은 부가서비스 혜택이 적용되는 여러 개의 가맹점 그룹을 하나로 통일할 수 있는 가능성을 열어 준다. 특별할인 업종은 여러 개의 가맹점 그룹으로 구성되어 있고 가맹점 그룹마다 할인율이 다르다. 그러나 매월 업종별 비중이 일정하므로 여러 개의 가맹점 그룹을 하나의 단일 업종으로, 여러 개의 할인율을 하나의 대표 할인율로 통합할 수 있다. 이것은 가중평균을 계산하는 과정과 같다.
무이자할부 이용금액에 할인혜택이 적용되지 않는 경우도 이 방법으로 간단히 해결할 수 있다. 즉, 어떤 업종에 적용되는 특별할인율이 10%이고 그 업종은 평균적으로 15%의 사용금액이 무이자할부라면 실질 적용 할인율은 8.5%가 되는 것이다. 이처럼 특별할인 가맹점 그룹을 하나의 업종으로 간주하고, 할인율을 단일화해도 정확성이 크게 떨어지지는 않는다. 모형의 최종 목적은 부가서비스 요율의 산출인데, 이것은 할인율보다 특별할인금액의 상한(한도)에 훨씬 더 큰 폭으로 영향을 받기 때문이다.
Table 6.
Consolidation of merchant groups into one single merchant group
4. 부가서비스 요율 예측 모형(VCPM)
4.1. 업종별 이용금액의 안정성
3장에서 브랜드 검색을 통해 현재 신용카드 업계에서 가장 주목받고 있는 카드 25종을 분석한 결과 카드별 부가서비스 제공 방식에 두드러진 5개의 공통 요소가 있음을 밝혔다. 또한 대부분 할인카드이므로 할인카드를 대상으로 분석하기로 하였다. 그리고 한국은행 자료를 이용하여 신용카드 실적은 월별로 업종별로 일정함을 살펴보았다. 이 덕분에 부가서비스 요율 예측은 어느 특정 한 달에 대한 예측만으로 충분함을 보였다.
월별 업종별 사용금액이 일정한 속성이 시장 전체가 아닌 특정 카드의 사용자 집단에 대해서도 유지되는지에 대한 직접 근거는 없다. 그러나 신한, 삼성 등 주요 카드사들의 회원은 천만 명을 넘는다. 브랜드 검색에 등장할 만큼 주요 카드들이라면 이 가운데 1/20만 신청하더라도 50만 명을 초과하므로 소수 사용자들의 이용행태가 전체 추세에 큰 영향을 끼칠 가능성이 매우 낮다.
또 지역별 소비유형별 신용카드 이용금액 자료는 지역별로 세분화 하여 산출해도 속성이 유지된다. 일례로 강원도는 총 인구가 154만 명(KOSIS, 2018)에 불과하므로 경제 인구만 감안한다면 위에서 예시한 단일 카드 사용자 집단(50만명)과 큰 차이가 없다. 이런 점들을 볼 때 업종별 실적이 일정한 속성은 특정 카드 사용자 집단에서도 유지된다고 가정할 수 있다.
4.2. 모형의 제시
부가서비스 요율 예측 모형은 prediction model for value proposition cost를 줄여 VCPM 모형으로 호칭한다. 3장에 제시된 특징들, 특히 (가정 1)과 (가정 2)를 반영하여 VCPM 모형을 구축한 결과는 <Table 7>과 같다. 모형이 최종적으로 산출하고자 하는 값은 R이다. 연산은 대부분 간단한 수식으로 이루어져 있고 S와 P는 특정한 확률분포를 따르는 것으로 가정하였다.
대문자로 표시된 변수는 일정한 분포를 따르는 확률변수 또는 확률변수들 간의 관계식을 의미한다. 또 문맥에 따라서는 개별 사용자의 값이나 전체 합을 의미하기도 한다. VCPM의 시뮬레이션 대상자 수(N)를 i = 1,2, ..., N으로 표시할 때 S는 월 신용카드 이용금액이라는 확률변수를 지칭하고, i번째 사용자의 이용금액(결정된 값)은 s(i)로 표시해야 옳다. 또한 월간 총 신용카드 이용금액(결정된 값)은 Σs(i)으로 나타내야 한다. 그러나 <Table 7>에서는 이 세 가지를 모두 S로 표시하였고 이같은 표기 관행은 다른 변수들도 마찬가지다. 앞으로도 특별히 혼동될 위험이 없는 한 이렇게 표기한다.
4.3. S와 P의 분포 가정
S와 P는 사용자들의 이용행태를 묘사하는 확률변수들이다. S는 한 달 동안의 총 이용금액이다. 앞서 살펴보았듯 신용카드 이용금액은 월별 업종별로 일정하므로 일정한 카드 사용자 집단이 일으킨 카드 이용금액은 특정 분포를 따를 것으로 추론된다. Lee and Roh(2018)는 신용카드 월 이용금액의 분포를 지수분포로 적합할 수 있음을 보였다. 이에 따르면 각 사용자들의 신용카드 이용금액은 S의 평균값의 역수를 파라미터(λ)로 하는 지수분포 난수로 생성 가능하다(Ross, 1990). 수식은 다음과 같다.
P는 전체 신용카드 이용금액 중 특별할인 가맹점에서 사용한 금액의 비율이다. P의 분포를 결정하는 것은 해당 카드의 미래 사용자들의 이용행태를 가정하는 것이다. P가 결정되면 R은 쉽게 계산된다. P는 확률변수이므로 P가 취하는 구체적인 값은 시뮬레이션 대상자별로 p(i)라고 표현해야 하나, 특별히 혼동될 염려가 없는 한 P로 표현한다.
P는 비율이므로 [0,1]의 값을 갖는다. 베타분포는 확률변수의 정의구역이 [0,1]이므로 비율 변수를 묘사할 때 자주 사용되지만 비율 변수가 형성하는 분포의 형태는 상황에 따라 달라지므로 꼭 베타분포를 쓸 수는 없다. 좀 더 일반적으로 P의 분포를 결정하기 위해서는 신용카드 이용거래를 특별할인 가맹점 이용금액과 일반할인 가맹점 이용금액으로 구분하는 과정이 필요하다.
이것은 결과가 두 개 중 하나로 나타나는 상황에 대한 모의실험으로 볼 수 있다. 이런 종류의 모의실험을 다룬 연구로는 나타날 수 있는 2개의 결과를 성공/실패 또는 생존/죽음으로 구분하여 분석한 기대수명 분포 연구와 생존분포 연구가 널리 알려져 있다. 전자는 지수분포를, 후자는 감마분포와 로그정규분포 등을 주로 사용한다(Law et al., 2000).
이들 분포는 모두 양의 왜도를 갖는 분포(positively skewed distribution)로서 확률분포함수가 오른쪽으로 긴 꼬리를 갖는 공통점이 있다. 지수분포는 일반적으로 공산품의 수명분포를 적절히 묘사하는 것으로 알려져 있는데, 신용카드 이용금액을 지수분포로 적합할 수 있다는 사실을 고려하면 P의 분포로 추천할 만하다. 감마분포와 로그정규분포도 다양한 상황에서 사용되므로(Cho, 2004) 감마분포와 로그정규분포 또한 P의 분포로 고려할만 하다.
3.4에서 전체 이용금액 중 특별할인 가맹점 이용금액의 비중(이하 K)은 최대 30% 정도임을 보였는데, 이것을 VCPM의 표기로 표현하면 S1/S가 되고, 정확하게는 다음과 같다.
이 때 K는 s1(i) (i = 1,2, ..., N)과 s(i), (i = 1,2, ..., N)의 값이 결정된 후 P를 가중 평균하여 산출한 값으로 볼 수 있다. 개별 사용자들의 P는 K값을 기준으로 작은 쪽에 많이 분포하는 것으로 보는 편이 자연스럽다. 한 달 동안 신용카드를 100만원을 쓸 때 P = 20%를 달성하기는 P = 70%를 달성하기보다 쉽기 때문이다. 따라서 P의 분포는 최빈값(mode)이 평균(mean)보다 작은 양의 왜도를 갖는 분포를 따르는 것으로 볼 수 있고 지수, 감마, 로그정규분포 등이 적합한 분포가 되는 것이다.
지수분포와 감마분포, 로그정규분포의 확률분포함수와 평균값을 한데 나타내면 <Table 8>과 같다. 감마분포는 지수분포의 확장형 분포로서 α와 λ의 관계에 따라 다양한 형태가 나타나는데 본 연구에서는 지수분포와의 차별성을 두기 위하여 정점(peak)이 P = 0%에서 나타나는 형태는 채택하지 않는다.
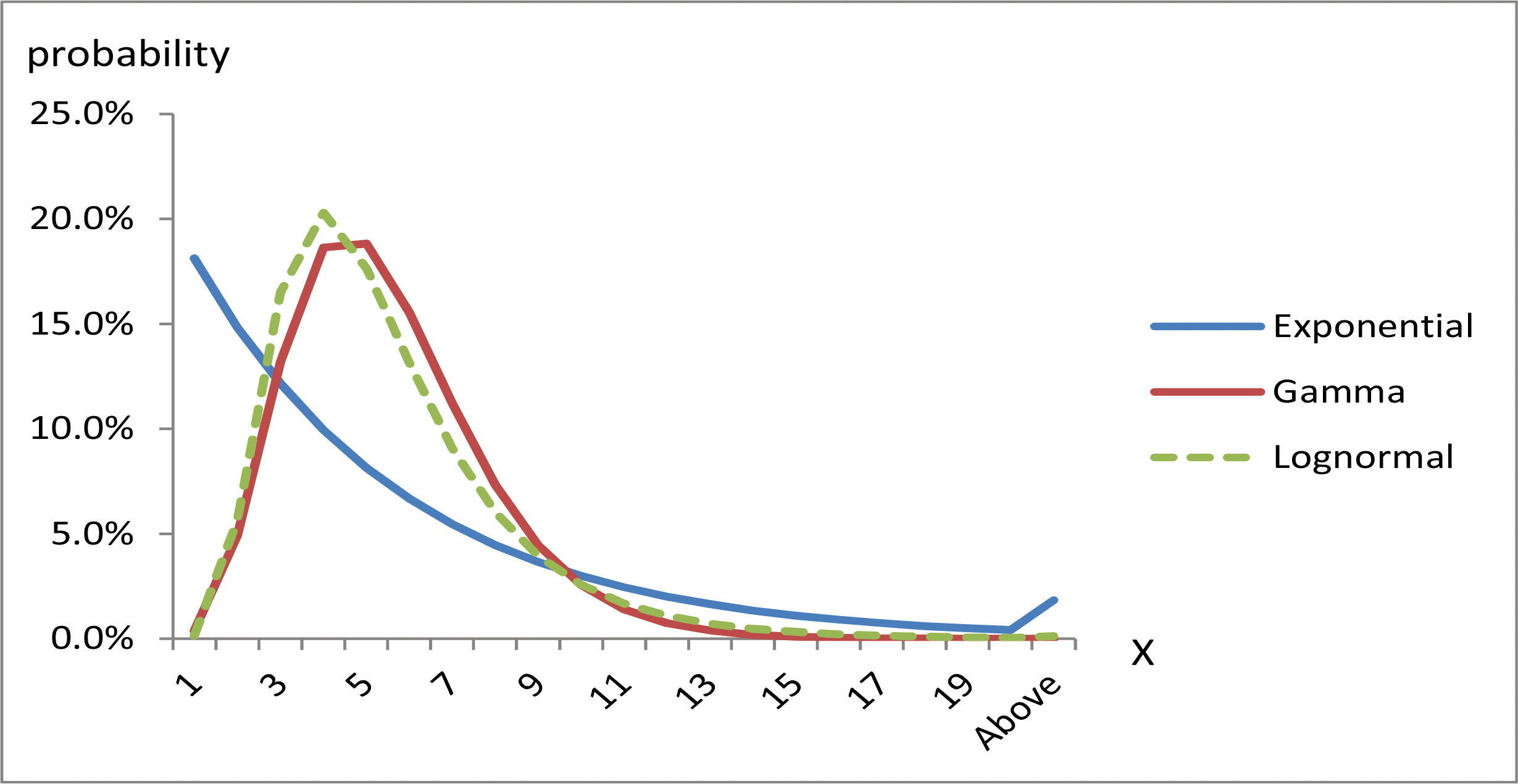
지수분포-감마분포-로그정규분포의 확률분포(PDF)를 도시하면 아래 그림과 같다. 일정한 파라미터 λ,α,μ,σ를 선정하여 E(X) = 5가 되도록 한 후 각각의 곡선을 한데 모으면 감마분포와 로그정규분포는 만곡률에 다소 차이가 있을뿐 상당히 유사한 형태임을 알 수 있다. 파라미터를 여러 가지 값으로 바꿔 가며 비교한 결과 로그정규분포는 대체로 정점이 감마분포보다 높고 곡선의 폭이 좁은 경우가 많았다. 처음에는 와이블 분포도 VCPM에 포함시키려 했으나 다른 분포들과 큰 차이가 없어 제외했다.
지금까지 P의 분포로 지수분포, 감마분포, 로그정규분포 등 양의 왜도분포를 채택한다고 기술했는데, 엄밀하게 표현하면 P를 생성하는 기저 난수(base random number)가 양의 왜도분포를 따르는 것이다. P는 ‘비율’이므로 1, 즉 100%를 넘을 수 없다. 따라서 P를 구하려면 우선 기저 난수를 세 가지 분포로 생성한 뒤 난수의 크기에 따라 12개 구간으로 나눠 첫 번째 구간은 P = 0%, 12번째 구간은 P = 100%로 할당하고 나머지 구간은 난수를 곧장 P의 값으로 할당하였다. 이렇게 하면 기저 난수는 (0, ∞)에 분포하고 P는 [0,1]에 분포한다.
기저 난수를 10등급이 아니라 12등급으로 나누는 이유는 P = 0%와 P = 100% 계급이 부가서비스 요율에 큰 영향을 미치기 때문이다. 따라서 P = 0%와 100% 계급을 별도로 설정하여 사용자 수를 할당해야 한다. 전자는 특별할인 가맹점에서 사용한 금액이 없는 카드 사용자들이고 후자는 신용카드 사용금액의 전부를 특별할인 가맹점에서만 이용한 카드 사용자들이다. P = 100% 계급의 사용자들은 부가서비스 혜택을 영리하게 취하는 집단이라는 측면에서 흔히 ‘체리피커’ 또는 ‘게이머(gamer)’라고 부르기도 한다.
이들의 존재 때문에 P의 분포는 다양한 형태가 나타날 수 있다. 그러나 일반 소비형 할인 카드에서는 지금까지 논의해 온 다양한 이용행태 속성에 따라 결국 양의 왜도분포와 비슷한 분포가 나타날 것으로 예상된다. 다만 주유카드나 백화점 카드 등 특수 목적 카드 또는 제휴 카드에서는 체리피커 그룹의 비중이 두드러지게 높을 것으로 예상된다. 이 예상들은 VCPM 모형의 추가적인 가정이다.
(가정 3) 일반적인 신용카드에서 P의 분포는 양의 왜도분포를 따른다
(가정 4) 제휴 카드에서 P의 분포는 체리피커 그룹의 비중이 높은 분포로 나타난다
4.4. 전월실적에 따라 u값 결정
VCPM 모형을 구성하는 또 하나의 중요한 요소는 특별할인한도(u)이다. 이것은 전월실적에 따라 사용자마다 차별적으로 적용된다. <Figure 3>은 브랜드 검색 대상 25종 카드 중 어느 한 카드의 특별할인 한도 안내 문구이다. 전월실적이 50만원 이상이면 1만원까지 할인을 해 주고 그렇지 못할 경우 혜택이 없음을 명시하고 있다. 따라서 전월실적이 52만원인 사용자는 최대 1만원까지 할인을 받고, 48만원인 사용자는 할인을 받지 못하게 된다.
특별할인한도(u)는 개인별로 다르게 적용되며, 그 결과 부가서비스 요율에도 큰 영향을 끼친다. 월 총 사용금액(S)은 지수분포 난수로 묘사가 가능하므로 전월실적도 같은 방식으로 생성하여 u의 계산에 사용하면 될 것 같지만 그렇게 할 수 없다. 왜냐하면 이달 사용금액과 전월 사용금액 사이에 어떤 상관관계가 있을지 알 수 없기 때문이다. 그러므로 전월실적과 이달 실적 간의 전이확률 행렬을 이용하여 u를 정해야 한다.
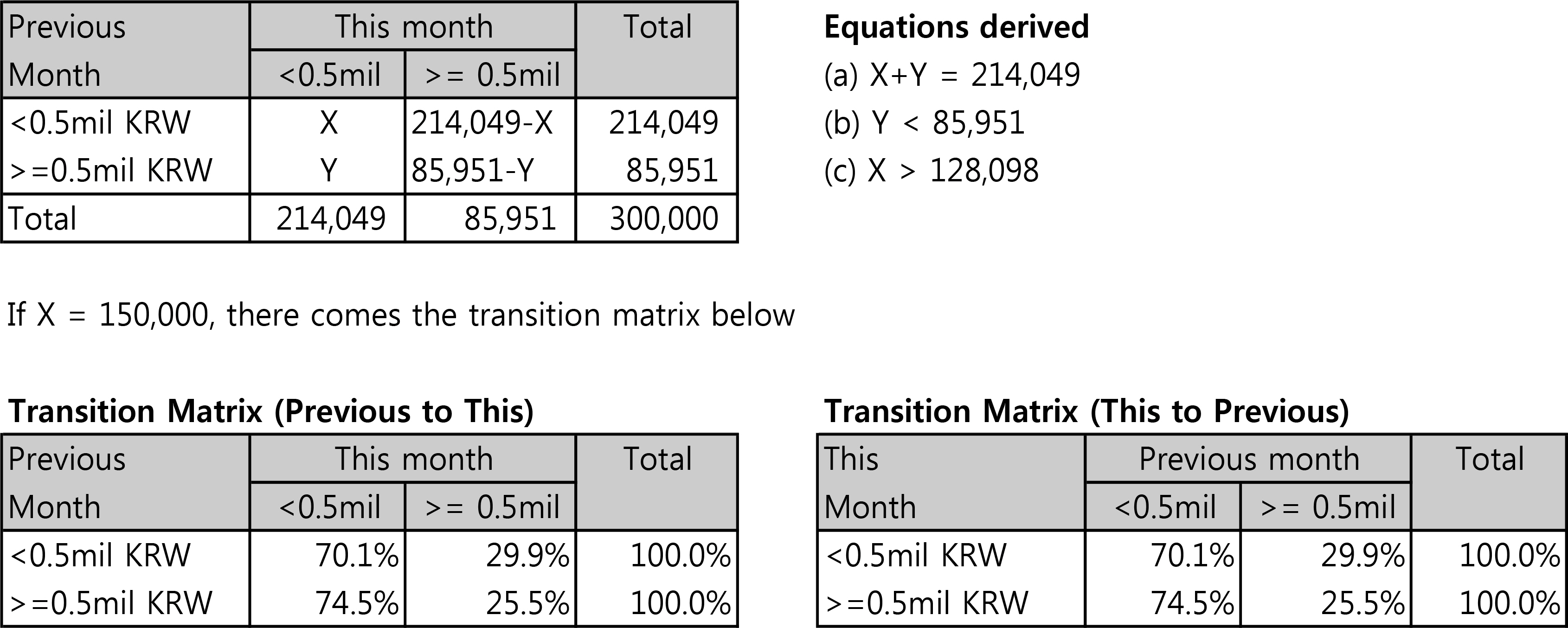
<Figure 3>의 조건을 예시로 계산하면 다음과 같다. 이 카드(A카드라고 부른다)의 사용자 집단은 30만 명이고 월 평균 사용금액은 40만원이라고 가정한다. 지수분포로 계산하면 71.3%에 해당하는 214,049명은 이달에 50만원 미만을 사용한다. 나머지 85,951명은 50만원 이상을 사용한다. 이 분포는 매월 일정하므로 전월에도 50만원 미만 사용자는 71.3%, 50만원 이상 사용자는 28.7%의 비율을 유지해야 한다.
이 속성을 사용하여 전월 이용금액대 → 이달 이용금액대 카드 사용자수 분포를 분할표로 구성하면 그것이 바로 전이확률 행렬이 된다. 그러나 부가서비스 요율 계산시에는 어느 한 달(이달)의 이용금액을 생성한 후 전월실적에 따라 u를 부여하므로 거꾸로 이달 이용금액대 → 전월이용금액대 카드 사용자수 분포를 분할표로 구성하여 전이확률 행렬로 쓰는 편이 편리하다. 그 과정을 <Figure 4>에 묘사하였다. 2X2의 경우에는 두 행렬이 서로 같지만 그 이상으로 확대하면 차이가 생긴다.
<Figure 4>는 매월 신용카드 이용금액 및 사용자의 분포가 일정하게 지수분포를 따른다는 속성(식 1)에 따라 A카드의 지표를 (1) 사용자 30만 명 (2) 월 평균 40만원 사용으로 놓고 계산한 것이다. 최종적인 전이확률 행렬은 X의 값을 알아야 결정할 수 있는데, 실제로 이 카드를 운용하는 카드사에서는 X값을 단 하나의 값으로 결정할 수 있는 자료가 존재하므로 그 값을 적용하여 전이확률 행렬을 결정하면 된다. (예시에서는 X = 150,000 적용)
연구자들은 X의 범위에 대한 정보만 알 수 있으므로 X의 값을 다양하게 바꿔가면서 실험을 해야 한다. 반복 실험 결과 전이확률 행렬이 달라지면 부가서비스 요율이 적지 않은 영향을 받는 것으로 나타났다. 따라서 전이확률 행렬을 결정하는 것은 매우 중요하다. 한편, 특별할인한도(u)를 부여하는 컷오프 값이 여러 개일 때도 유사한 방법으로 전이확률 행렬을 산출하면 된다.
4.5. 가상의 카드의 value proposition
이제 실제로 VCPM 모형이 부가서비스 요율 예측에 어느 정도 효용이 있는지 살펴 볼 차례다. 현재 신용카드 이용행태에 관한 개인별 데이터는 공식적으로 구할 수 없다. 2011년 9월 발효된 개인정보보호법에 의해 사실상 길이 막혀 있기 때문이다. 그러나 법령이 완화되고, 신용카드사들이 데이터를 외부에 적극적으로 제공하는 시대가 오더라도 요율 산출에 필요한 데이터를 원활하게 얻기는 힘들다.
왜냐하면 전체 사용금액을 특별할인 가맹점 실적과 일반할인 가맹점 실적으로 구분하려면 가맹점 정보가 정확하게 관리되어야 하는데 우리나라는 프랜차이즈의 생성과 소멸이 심하여 관리가 쉽지 않기 때문이다. 부가서비스 안내문구에 흔히 “당사의 가맹점 등록 기준”으로 혜택을 제공한다는 구절이 있는 이유이다.
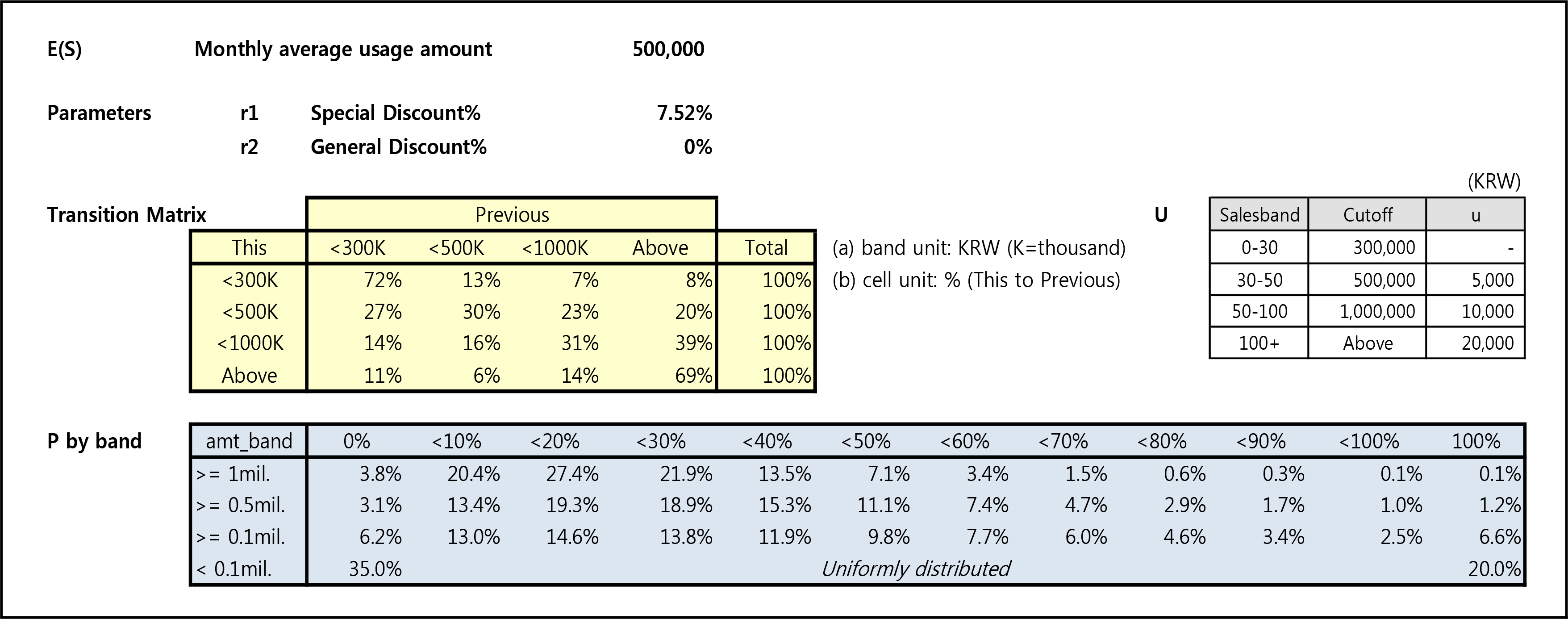
카드사에서 부가서비스 요율 분석을 할 때도 특정 시점에 가맹점 정보를 집계하고 그것을 바탕으로 제한된 횟수의 분석을 수행할 뿐이다. 따라서 본 연구에서는 가상의 실 데이터들을 생성하고 각각 VCPM 모형이 산출한 요율과 비교하고자 한다. 여기서 ‘가상의 실제’로 설정한 카드의 부가서비스 내역(value proposition)은 <Figure 5>와 같다. 아래 값들은 확률분포로 연산해야 하는 P by band 이외에는 알려진 값들이라고 가정했는데, 카드사에서 이 정도 값들은 경험적으로 산출 가능하다.
4.6. 시나리오 1~3 시뮬레이션 결과
브랜드 검색으로 살펴 본 25종의 카드 중 대다수를 차지하는 것은 일반형 할인 카드였다. 이 유형의 카드는 (가정 3)에 따라 P가 하나의 양의 왜도분포를 따르는 것으로 적용해도 되지만, 이용금액대별로 분포를 달리하여 현실성을 높이는 것이 보다 바람직하다. 상식적으로 월 이용금액이 10만원(0.1 mil. KRW) 이하인 사용자 그룹의 상당수는 체리피커일 것이다. 왜냐하면 이들은 주사용카드는 따로 있고 이 카드는 특정 혜택만을 위해 사용할 가능성이 높기 때문이다.
따라서 이 금액대의 사용자들은 체리피커의 비중을 높이고, 그 이상 금액대 그룹에서는 P가 자연발생적인 양의 왜도분포를 따르도록 구성하였다. 이런 방식으로 시나리오 1~3별로 각각 P의 분포를 조금씩 달리 설정하였다(Appendix 1 참조). P의 분포가 결정되면 반복 연산을 100회 수행하여 분포를 대표하는 하나의 K값(식 2)을 산출한다. 이 값은 VCPM의 각 모형별 K값과 구별하기 위해 Ks로 표기한다. 여기서 반복 연산이란 P의 기저 난수들을 새롭게 생성하는 과정을 의미한다.
예를 들어, 사용자 집단이 1만명이라면 매 연산마다 1만 개의 지수분포 난수를 발생하여 S를 산출하고, 다시 1만개의 난수들을 발생하여 P를, 다시 말해 p(i) (i = 1,2, ..., N)를 산출한다. 이렇게 하면 사용자 집단 전체의 K값은 첫 번째 연산 때는 29.5%, 두 번째 연산 때는 30.1% 등으로 나타날 수 있다. 이 같은 연산을 100회 수행하여 나온 평균값을 Ks로 채택한다.
그 다음 이 Ks에 가까운 값이 나오는 지수분포, 감마분포, 로그정규분포의 파라미터 값을 반복 연산을 통해 탐색한다. 지수분포는 파라미터가 λ 하나뿐이므로 단 하나의 값을 선택하고 나머지 두 분포는 파라미터가 두 개씩이므로 상위 3개를 선택하여 VCPM 모형에 적용하였다. 시나리오 1~3은 P의 분포만 달리 하고 <Figure 5>에 제시된 다른 입력값들은 모두 동일하게 적용하였다.
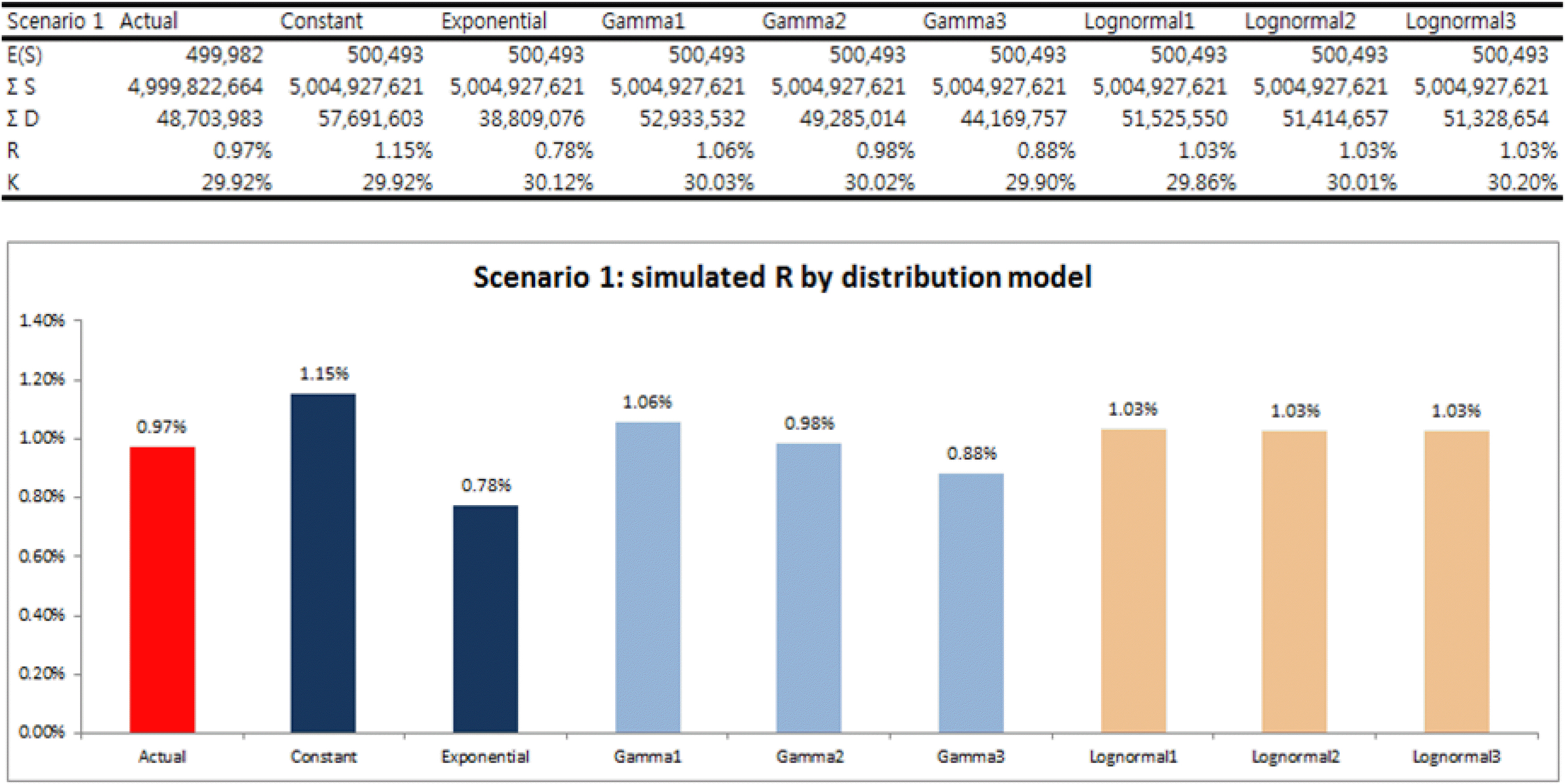
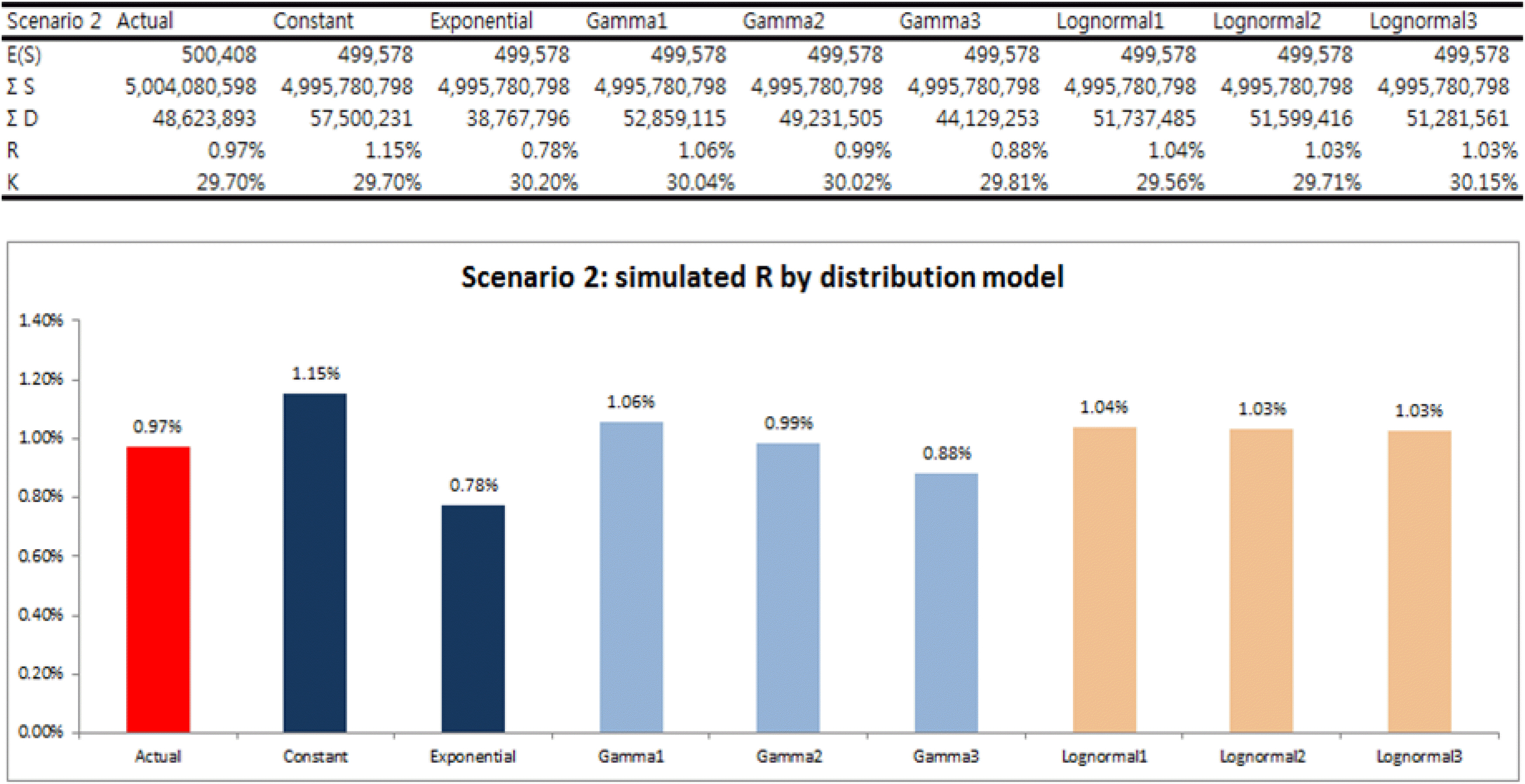
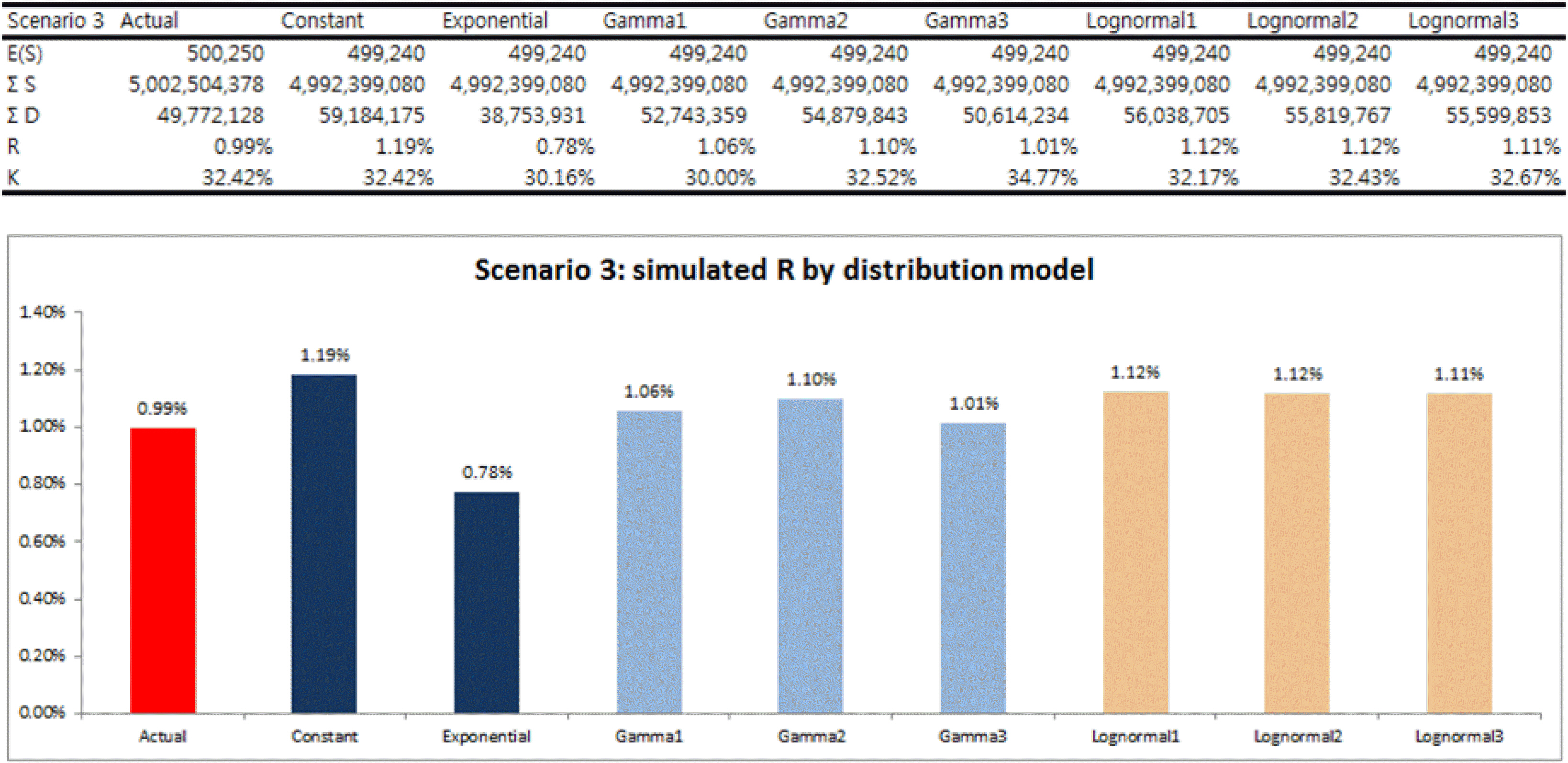
이런 과정을 통해 카드 사용자 수 1만 명에 대해 반복 연산을 수행한 결과 Ks는 시나리오 1이 29.92%, 시나리오 2가 29.70%, 시나리오 3이 32.42%로 나타났다. 그리고 시나리오별 부가서비스 요율(R)은 각각 0.974%, 0.972%, 0.995%로 산출되었다. 이 값들을 ‘가상의 실제값’으로 보고 VCPM 모형에서 산출되는 요율과 비교하였다.
VCPM 모형은 지수분포, 감마분포, 로그정규분포 모형 외에 1만 명의 사용자들이 모두 동일한 대표 P값을 갖는 상수 모형을 추가하였고 감마분포, 로그정규분포는 각각 3개씩의 파라미터를 선정하였으므로 총 8가지 모형을 구축, 가상의 실제값과 비교하였다. 시뮬레이션의 구체적인 단계는 Appendix 2에 상술하였다.
시뮬레이션 수행 결과 각 모형별 K값(전체 이용금액 중 특별할인 가맹점 이용금액의 비중)은 모두 Ks와 아주 가까운 값이 나타났고 부가서비스 요율(R)은 가상의 실제 R값이 상수 분포와 지수분포의 평균 정도로 나타났다. 감마분포와 로그정규분포에서 도출된 R값들도 시나리오 1~3에서는 가상의 실제 R과 유사했으나 추가로 고려한 다른 시나리오들에서는 실제 R과 차이가 적지 않은 경우도 있었다.
시뮬레이션 결과 항상 상수 분포로 산출한 R값이 가장 높았다. 그리고 지수분포로 산출한 R값이 가장 낮았다. 감마분포와 로그정규분포 모형은 정점(peak)이 높은 순서에서 낮은 순서로 배치했다. 즉 Gamma1 모형이 Gamma3 모형보다 분포곡선의 봉우리가 높고 P의 편차가 작다. 그래프에서 보듯 각 모형의 R값들은 모두 가상의 실제 R값과 유사하게 나타났다. 그러나 어느 하나가 일관성 있게 가장 가까운 값을 생성하지는 않으므로 실제 R과의 관계를 설명하기는 어렵다.
유일하게 안정적인 현상은 가상의 실제 R값이 항상 상수 분포로 도출된 값과 지수분포로 도출된 값의 평균 정도에 위치하는 것이었다. 이는 상수 분포 모형에서 도출된 R과 지수 분포 모형에서 도출된 R이 각각 실제 R값의 상한과 하한 같은 역할을 하기 때문에 나타나는 현상으로 해석된다. 상한과 하한의 차이가 아주 크지는 않으므로 그 평균은 상, 하한보다 실제 R값에 가까워지는 것이다.
결과적으로, 분포별 일치 성향과 관계없이 VCPM 모형은 일반 소비형 할인 카드에 대해서는 부가서비스 요율을 신뢰할 수 있을 만큼 안정적인 수준으로 산출하는 것으로 나타났다. 또한 부가서비스 요율의 상한과 하한을 제시하므로 불확실성의 크기를 가늠할 수 있게 해 주어 실무적인 효용을 배가시켰다고 볼 수 있다.
4.7. 시나리오 4 시뮬레이션 결과
한편 주유카드, 백화점 제휴 카드 같은 특수 목적형 카드는 P가 양의 왜도분포가 아니라 다른 형태의 분포로 나타날 것으로 예상된다. (가정 4)에서 이런 카드들은 체리피커 그룹의 비중이 높다고 하였는데, 실제로도 주유카드 사용자는 주유에만, 백화점 제휴 카드는 해당 백화점에서만 카드를 사용하는 비중이 높을 가능성이 크다.
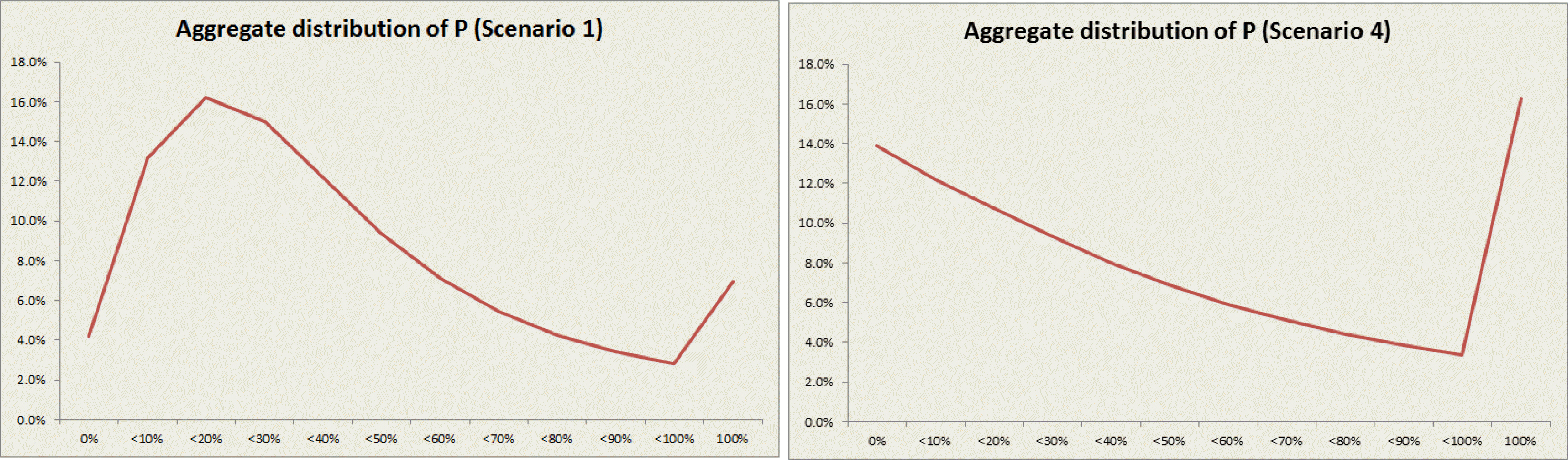
그런 상황을 가상하여 시나리오 4를 가지고 시뮬레이션을 실시하였다. P = 100%인 그룹의 비율이 16.3%나 되도록 P의 분포를 구성한 결과 Ks는 49.82%가 산출되었다. 앞서 시나리오 1~3은 Ks가 30% 전후에서 형성된 것과 대조적이다. 다시 말해 전체 신용카드 사용금액의 절반을 주유할 때만 사용했다는 뜻이다. 소비자의 이용행태가 이런 극단적인 분포를 보이면 양의 왜도분포를 기반으로 구성된 VCPM 모형은 부가서비스 요율을 제대로 예측할 수 없다.
시뮬레이션 결과 가상의 실제 R값은 1.0%인데 반해 상수 분포로 산출한 R = 1.32%와 지수분포로 산출한 R = 1.01%로 항상 최소의 R값을 산출하는 지수분포조차도 실제 R값을 포함하지 못하였다. 이런 결과는 소비자의 이용 행태를 나타내는 P의 분포가 극명한 차이를 보이기 때문인데, 시나리오 1와 시나리오 4의 P 분포를 대조하면 그 차이를 쉽게 알 수 있다.
지금까지 일반 할인형 카드를 위주로 설명하였는데, 포인트 적립형 카드와 항공 마일리지 카드에도 VCPM 모형을 적용할 수 있다. 포인트 적립형 카드는 포인트당 단가를 적용하면 되므로 VCPM 모형의 D값 계산 단계에서 공식을
로 바꾸면 곧바로 적용할 수 있다. 항공 마일리지 카드는 위 식의 (cost/point) 자리에 1마일리지당 단가(cost/mileage)를 곱하면 된다.
항공카드는 이용행태가 어떻게 나타날지 예단할 수 없다. 마일리지 적립 혜택을 주는 가맹점이 다양한 항공카드는 일반형 카드와 유사한 행태가 나타날 것이고 적립 혜택을 주는 가맹점이 적은 항공카드는 주유카드, 백화점 카드 등과 비슷한 행태가 될 것이다. 항공카드는 마일리지가 적립되는 카드라는 공통점 외에는 카드사마다, 상품마다 타겟 고객과 상품 포지셔닝이 달라 일반화하기 어렵다.
4.8. 실무적 시사점
부가서비스 요율을 데이터마이닝 방식으로 계산하려면 수많은 사용자들의 행태 데이터를 일일이 만들어야 하는 번거로움이 있다. 기존 사용자들 중에서 신규 카드와 유사한 행태를 보이는 것으로 판단되는 사용자들을 추출하여 그들의 일정 기간 동안의 이용 행태 자료를 산출, 계산하는 단계를 거치게 되는데 다양한 상황별로 데이터를 따로 준비해야 하므로 시간도 많이 걸리고 예측 효율도 낮다.
VCPM은 미래 사용자 그룹의 월 평균 이용금액, 전체 이용금액 대비 특별할인 가맹점 이용금액의 비중 등 몇 가지 값만 결정되면 손쉽게 부가서비스 요율의 범위을 구할 수 있다. 뿐만 아니라 S와 P의 분포의 파라미터를 변경해가면서 다양한 민감도 분석을 수행하면 최악의 상황을 예측하고 미리 대비할 수 있다. 월 평균 50만원, 월 평균 사용자 15만 명인 카드의 부가서비스 요율을 1%로 예측했다가 출시 후 1.5%가 나온다면 당장 월 3억 7,500만원의 추가비용이 소요되므로 부가서비스 요율을 정확히 예측하는 것은 매우 중요하다.
이처럼 부가서비스 요율은 손익 분석에 지대한 영향을 끼치는 변수이고, 사용자 입장에서는 서비스 품질의 지표이다. 부가서비스 요율이 높으면 그만큼 사용자에게 돌아가는 혜택이 많고, 고객만족도가 높다는 뜻이므로 부가서비스요율은 너무 낮아서도 안 된다. 요율이 낮은 카드는 손해를 보지는 않겠지만 인기가 없으므로 판매가 부진하여 결국 단종의 길로 접어들 수 있다. 따라서 부가서비스 요율은 카드상품 출시의 가부를 결정짓는 단 하나의 KPI로도 사용될 수 있다.
사전 진단 결과 부가서비스 요율이 너무 높으면 혜택 가맹점 일부를 제외할 수도, 또 반대의 경우는 추가할 수도 있다. 이것은 부가서비스 요율이 비즈니스 전략 의사 결정의 도구로 사용되는 사례이다. 부가서비스 요율은 활용도가 높은 지표이므로 정확한 예측이 필수적이고, 그런 맥락에서 VCPM 모형의 가치를 평가할 수 있다.
5. 결 론
국내 소비 시장에서 신용카드는 점점 더 큰 비중을 차지하고 있으나 수익성은 악화되고 있다. 그 원인 중 큰 비중을 차지하고 있는 부가서비스는 카드사 스스로가 제어할 수 있는 항목이므로 새 카드 출시 후 비용 수준이 어느 정도가 될지 체계적인 분석이 필요하다. 또한 부가서비스 요율을 잘못 예측하여 단기간 내에 서비스를 축소하고 심지어 카드 상품을 폐쇄했던 과거에 비춰 보더라도 부가서비스를 이용하는 사용자들의 행태에 관한 연구는 절실한 상황이다.
미지의 집단에 대한 거시적인 행태 연구에는 확률분포를 이용한 방법론이 적절하다. 그러나 카드사들은 데이터마이닝을 위주로 한 방법론에 치중하고 있는데, 이것은 그 속성을 이미 알고 있는 집단의 행태 진단에 강점이 있을 뿐, 신규 카드 출시 후 형성될 새 사용자 집단의 행태를 예측하는 데는 효율적이지 않다.
이에 본 연구는 확률분포를 이용한 부가서비스 요율 예측 모형(VCPM 모형)을 구축하고, 카드의 부가서비스 혜택(value proposition)에 따라 요율이 어느 정도 수준이 될지 계산하는 시뮬레이션 모형을 제안하였다. 실험 결과 전체 신용카드 이용금액 중 특별할인 가맹점에서 사용한 이용금액의 비중이 오른쪽으로 꼬리가 긴 양의 왜도를 갖는 분포로 나타날 때는 VCPM 모형이 부가서비스 요율을 상당히 정확하게 계산해 주는 것으로 나타났다. 그리고 특별할인율이 일반할인율보다 높은 한, 상수 모형은 최대값을, 지수분포 모형은 최소값을 나타냄으로써 실제 부가서비스 요율의 적정 범위를 산출할 수 있는 가능성도 제시하였다.
본 연구는 부가서비스 요율의 개념과 산출에 관한 주제를 다룬 것으로는 최초이며, 사실상 신용카드 부가서비스라는 연구 주제를 정량적으로 접근한 첫 번째 시도라고 할 수 있다. 본 연구의 한계점은 일반 소비형 카드에 초점을 맞췄다는 점이다. 일정 기간 동안의 브랜드 검색 결과 다수를 차지한 카드 그룹을 대상으로 연구를 진행하였고, 그들은 다수가 양의 왜도분포를 나타낼 것으로 기대되는 일반 소비형 할인 카드이므로 본 연구와 결과는 그 카드 그룹에 대해서만 유효하다.
주유카드, 백화점 카드, 일부 항공카드 같은 특수목적 카드나 제휴 카드에 대해서는 이용패턴을 예단할 수 없는 한계가 있었다. 하지만 이용행태에 따라 VCPM 모형이 차별적으로 구축되어야 한다는 사실을 밝힌 것은 또 다른 형태의 발견이라고 여겨진다. 후속 연구자들은 본 연구에서 다루지 못한 유형의 카드들에 대해서도 효과적인 부가서비스 요율 예측 모형을 도출하여 향후에는 카드사들이 소비자의 의사에 반하여 부가서비스를 해지하거나 시장에서 인기 있는 카드 상품을 단기간 만에 없애는 관행이 없어지기를 기대한다.