최근 다양한 분야에서 Modeling & Simulation (M&S) 기술을 과거보다 더 활발히 활용하고 있다. 제조분야, 국방분야, 의료분야, 건축분야 등 거의 모든 분야에서 M&S 기술을 접목하여 기존 기술의 한계점을 극복하고자 하는 노력을 기울이고 있다. 이러한 M&S 기술을 접목하는 분야들의 공통은 우리가 다루는 대상시스템(Target System)이 매우 고가이거나 혹은 매우 위험하다는데 있다. 즉 대상시스템이 너무 고가이거나 너무 위험해서 실제 시스템을 대상으로 수행하는 실험을 최소한으로 줄여야 할 필요가 있을 때, 모의실험(M&S)을 수행하는 것이다 (Kang et al., 2005; Keane et al., 2000).

특히 국방분야는 대표적으로 대상시스템이 매우 고가이고 매우 위험하다고 할 수 있으며, 따라서 M&S 기술의 적극적 활용이 불가피하다고 할 수 있다. 최근 국방분야에서는 미래전투체계 (FCS: Future Combat System) 개념이 많은 주목을 받고 있다. 이는 최근 전쟁의 양상이 전면전 보다는 다양한 형태의 국지분쟁의 형태로 일어남에 따라 이에 효과적으로 대응하고자 다양하고도 맞춤형 수단과 능력을 보유한 자율제어시스템(Autonomous Control System)을 운용하는 것을 골자로 하고 있다. 여기에는 무인 수상정 (Unmanned Surface Vehicle), 무인 비행기(Unmanned Aerial Vehicle), 단거리 포, 그리고 다양한 표적 획득 수단 등이 포함된다 (Figure 1). 이러한 고가의 무기체계를 개발 혹은 도입하기 이전에 정량적 무기체계 효과도 분석을 수행하여 소요 군이 원하는 목표수준의 효과를 달성 할 수 있는지를 검증하는 것이 매우 중요하다 (Jung et al., 2017).

이러한 자율제어시스템 무기체계의 효과도 검증을 위해서는 무기체계가 배치, 운용되는 자연환경뿐만 아니라, 무기체계 자체의 물리적 특성과 논리적 특성이 잘 고려되어야 한다. 즉 정합성이 보장되는 시뮬레이션 모델의 구축 없이는, 무기체계 효과도 검증은 있을 수 없다. 정합성 높은 시뮬레이션 모델의 구축 방법론은 기존에도 많은 연구가 있어왔으며 특히 전통적으로 제조 분야에서 많은 기존 연구가 존재한다. 기존 제안된 모델링 formalism중에는 애리조나 대학교의 Bernard P. Zeigler가 고안한 DEVS (Discrete Event System Specification) formalism (Kim, 1994; Zeigler, 1984)이 있으며, 객체지향적이며 계층구조를 효과적으로 지원함으로써 다양한 분야에서 정합성 높은 시뮬레이션 모델 구축에 활발히 사용되었다. 특히 국방분야 및 제조분야를 비롯한 다양한 분야에 적용되어 모델링 및 시뮬레이션 연구가 수행되고 있다.

제조분야에서는 DEVS formalism을 채택하여 생산시스템에 대한 이산사건모델을 작성하여 실제 제어시스템과 연동하는 Hardware-in-the-Simulation 기술이 제안된 바 있다 (Park and Chang, 2012). 제조분야 이외에도 특히 국방 분야에서 많이 활용되었는데, 합성환경 분야 (Park and Seong, 2010; Yang et al., 2013), 무기체계 효과도 검증 분야 (Kim and Park, 2015; Ham et al., 2014; Lee et al., 2014), 그리고 시나리오 생성분야 (Park et al., 2013)등에 활용된 바 있다. 이처럼 DEVS formalism의 활용은 다양한 분야에서 이루어지고 있으며, 무기체계의 모델링 및 시뮬레이션에 관한 연구도 다양한 접근방법으로 수행되고 있다. 또한 특정 목적을 위해 classic DEVS formalism을 확장한 연구도 다양하게 존재한다. 대표적으로는 Stochastic DEVS (Castro et al., 2010), Dynamic DEVS (Barros, 1997), Real Time DEVS (Hong et al., 1997), Fuzzy DEVS (Kwon et al., 1996), 그리고 Vectorial DEVS (Bergero and Kofman, 2014) 등이 있다.

이처럼 기존에 DEVS formalism을 적용하여 무기체계의 시뮬레이션에 적용하는 다양한 연구가 있어왔지만 최근 도입되고 있는 자율제어시스템의 효과적 모델링 및 시뮬레이션에 대한 연구는 부족한 실정이다. 기존의 classic DEVS formalism을 자율제어시스템의 모델링에 적용하게 되면 몇 가지 곤란한 부분에 부딪히게 된다. 대표적으로 자율제어시스템은 자체적으로 상황을 판단하여 시스템의 상태를 전환하게 되는데, classic DEVS formalism은 이러한 상태분기에 대한 고려가 충분하지 않다.

본 연구의 목표는 자율제어시스템을 효과적으로 모델링 할 수 있도록 classic DEVS formalism을 확장하는 것이다. 확장된 DEVS formalism은 특히 자율제어시스템의 주변상황 혹은 내부적인 조건에 의해 가변성을 포함하는 행위나 작업들을 효과적으로 모델링 할 수 있어야 한다. 본 논문의 구성은 다음과 같다. 2장에서는 classic DEVS formalism에 대해 설명하며, classic DEVS formalism을 보완할 수 있는 방안에 대해 기술한다. 3장에서는 DEVS formalism의 확장된 형태인 C-DEVS formalism에 대해 기술한다. 4장에서는 C-DEVS formalism을 이용한 수상함 기동모델에 대해 기술하며, 5장에서 본 연구에 대한 결론으로 마무리한다.

이산사건시스템을 기술하여 모델을 구축하는 모델링 방법론에는 DEVS formalism, Event Graph, Petri-Net, Activity Cycle Diagram 그리고 Finite State Automata 등 여러 가지가 있다. 이러한 모델링 방법론들은 모두 각각의 장.단점을 가지고 있지만 서로 다른 형식으로 변환될 수 있으면 그에 관한 연구도 있다 (Choi and Kang, 2013). 이러한 다양한 모델링 방법론 중에서 DEVS formalism은 두 가지 대표적 장점을 가지고 있는데, 첫 번째는 문법적 엄격성이고 두 번째는 모델의 계층적 구조 구축을 가능하게 한다는 것이다 (Zeigler, 1984). 본 연구에서는 DEVS formalism을 자율제어시스템의 모델링에 효율적으로 적용하기 위해 확장하는 방안을 제안하고자 한다.

DEVS formalism에서 하나의 전체 시스템은 Atomic 모델 (Figure 2-(a))과 Coupled모델 (Figure 2-(b))로 구성되어 있다. DEVS의 Atomic 모델은 대상 시스템의 상태를 S (State)로 표현한다. State는 외부의 입력이 들어오거나 혹은 정해진 시간이 흐르면 다른 State로 변화한다. 모델링 기술은 대상 시스템을 이해하고, 분석하여 대상시스템의 State를 어떻게 나눌 것이고 언제 State의 변화가 일어나는 지에 대한 정의를 내리는 작업이라고 할 수 있다. Atomic 모델은 다음의 7개의 요소로 정의된다.

AM = <X, Y, S, δ_int, δ_ext, λ, ta>

· X : 이산사건 입력 집합

· Y : 이산사건 출력 집합

· S : 일련의 이산사건 상태의 집합

· δ_int: S → S 내부 상태 전이 함수

· δ_ext: Q × X → S 외부 상태 전이 함수

Q = {(s, e) | s ∈ S, 0 ≤ e ≤ ta(s)} : total state of M

· λ : Q → Y : 출력 함수

· ta : S → R[0,∞]:시간 진행 함수

Atomic 모델은 세 개의 집합과 네 개의 함수로 구성되어 있다. 세 개가 집합 (X, Y, S)는 각각 입력, 출력, 그리고 상태집합을 나타낸다. 네 개의 함수 중에 외부 상태 전이 함수(δ_ext)는 외부의 입력에 반응해서 상태변화를 일으키는 역할을 수행하며, 내부 상태 전이 함수(δ_int)는 일정시간이 경과한 후 자체적으로 상태변화가 일어나는 것을 표현한다. 자율제어시스템의 경우는 “외부의 간섭 없이 스스로 상황변화를 인지”하고 결정하는 경우가 많은데, 이러한 특징을 기존 내부 상태 전이 함수(δ_int)만으로 표현하기에는 어려움이 있다. 기존 내부 상태 전이 함수(δ_int)는 정해진 시간이 경과하면 상태변화를 일으킨다. 이를 바꾸어 말하면 기존 내부 상태 전이 함수(δ_int)는 내적인 상태변화에 소요되는 시간을 이미 알고 있다고 가정하고 있다는 것이다. 하지만 자율제어시스템의 경우 이러한 가정이 성립되지 않는 경우가 많다. 주어진 자연환경의 변화를 실시간으로 고려하여 임무를 수행하는 자율제어시스템의 경우 특정 임무를 수행하는데 걸리는 시간을 미리 알 수가 없기 때문이다. 따라서 “외부의 간섭 없이 스스로 상황변화를 인지”하는 자율제어 시스템의 특징을 잘 표현하기 위해서는 classic DEVS formalism의 내부 상태 전이 함수(δ_int) 관련 사항들을 확장할 필요가 있다는 것을 알 수 있다.

Coupled 모델은 Atomic 모델 간 혹은 이미 작성된 DEVS 모델들을 연결하여 상위의 시스템을 만들고, 또 그 시스템이 더 큰 시스템의 모듈로 사용될 수 있도록 하는 기능을 제공한다. 따라서, DEVS formalism을 사용할 경우 모델을 모듈화(Modular)하고 계층적으로 개발할 수 있다. Coupled 모델은 다음 7개의 요소로 정의된다.

CM = <X, Y, Mi, EIC, EOC, IC, SELECT>

· X: 이산 사건 입력 집합

· Y: 이산 사건 출력 집합

· Mi:구성요소 모델(원자 혹은 결합 모델) 집합

· EIC: 외부입력 연결 명세(External Input Coupling)

· EOC: 외부출력 연결 명세(External Output Coupling)

· IC: 내부 연결 명세(Internal Coupling)

· Select: 우선순위 함수(Select Function) = 2^Mi→Mi:같은 시간에 발생하는 사건에 대해 모델간의 우선순위를 결정하는 선택 함수.

이러한 classic DEVS formalism을 자율제어시스템인 USV (Unmanned Surface Vehicle)에 적용한다고 가정해보자. 매우 간단한 시나리오로 USV는 특정 출발지점 P(P_X,P_Y,P_Z)에서 출발신호를 받으면 목적지인 T(T_X,T_Y,T_Z)지점까지 이동한 후에 멈추는 것이다. 매우 간단한 시나리오 임에도 불구하고 하나의 Atomic 모델로 표현하기가 곤란함을 알 수 있다 (Figure 3). Classic DEVS 모델에서는 상태변화를 일으키는 것은 외부 상태 전이 함수 (δ_ext) 및 내부 상태 전이함수 (δ_int)의 두 가지 경우뿐이다. 첫 번째 외부 상태 전이 함수로 목적지점에 도착한 상황을 표현하는 것은 “외부의 간섭 없이 스스로 상황변화를 인지”하는 자율제어시스템의 특징에 전혀 부합되지 않는다. 그렇다면 내부 상태 전이 함수로 목적지에 도착했다는 것을 표현해야 하는데, classic DEVS의 내부 상태 전이 함수는 상태 변화에 소요되는 시간을 미리 알고 있다는 가정을 전제로 하고 있다. 예를 들어 USV의 임무 수행에 영향을 미치는 자연환경은 파고, 바람의 방향과 속도 등을 들 수 있는데, 이러한 상황이 실시간으로 바뀔 때 상태 전이에 필요한 시간을 미리 알고 있다고 하는 가정은 성립되기 곤란하다. 본 논문에서는 “외부의 간섭 없이 스스로 상황변화를 인지”하는 자율제어시스템 효과적 시뮬레이션 모델링을 위해 classic DEVS formalism을 확장하여 C-DEVS formalism을 제안하도록 한다.

앞서 언급한 자율제어시스템 모델링에 있어서 나타날 수 있는 classic DEVS formalism의 어려움을 보완하기 위해서는 자율적인 논리와 행위를 표현 할 수 있어야 한다. 자율적인 논리와 행위라는 것은 자율제어시스템이 내부적으로 주어진 조건을 고려하여 의사결정을 내리고 임무를 수행하는 것을 의미한다. 예를 들어 USV가 주어진 목표지점에 도착했는지, 또한 전방에 적이 발견되었는지, 그리고 적이 사정거리 내에 있는지와 같은 조건을 내부적으로 고려할 수 있어야 한다. 이러한 조건들을 표현하기 위해서는 하나 이상의 조건변수(Conditional Variable)를 고려할 수 있어야 하지만, classic DEVS formalism 에서는 이러한 조건변수에 대한 개념을 가지지 않으며, 오직 시스템의 상태를 Sequential states set으로 만 표현하고 있어서 이러한 자율적 조건 분기의 효율적 표현이 곤란한 것이다. 조건 변수의 개념이 없는 classic DEVS formalism의 Sequential states set으로 자율제어시스템의 다양한 상태를 표현하게 되면 State 개수가 폭발적으로 늘어나는 ‘State explosion’ 문제가 발생할 위험이 매우 크다.

이러한 어려움을 극복하기 위하여, 본 연구에서는 자율적인 논리와 행위를 모델링 할 수 있도록 새로운 형태의 조건분기 상태(CS, Conditional State)와 조건변수(CV, Conditional Variable) 개념을 차용하여 classic DEVS formalism을 확장하였다. 조건변수(CV)를 이용하여 조건분기 상태(CS)의 상태전이가 정의되고, 이를 통해 자율제어시스템의 자율적인 논리 및 행위를 효과적으로 모델링 할 수 있게 한다.

Classic DEVS Atomic 모델은 세 개의 집합과 네 개의 함수로 정의되지만, 확장된 C-DEVS Atomic 모델에서는 기존 구성요소인 세 개의 집합과 네 개의 함수에 추가하여 조건분기상태 집합(CS), 조건변수집합(CV) 그리고 특정분기조건을 표현하기 위한 조건공간집합(C)을 추가로 도입한다. 조건공간집합(C)은 조건변수집합의 조합으로 표현되는 공간이며 조건변수의 개수가 n이라면 조건공간집합은 n-dimensional conditional space가 된다.

Classic DEVS formalism에서는 주어진 상태에서 상태의 전이가 일어나는 경우는 외부에 의한 사건 발생이나 내부적인 시간흐름에 의해서만 상태 전이가 이루어진다. C-DEVS formalism에서는 현재의 상태에서 주어진 조건에 대한 판단으로 상태의 전이가 일어날 수 있으며, 조건에 의해 전이되는 상태도 달라질 수 있다. 언급한 조건적 이산사건 상태와 조건을 위한 변수의 집합 그리고 조건적 상태 전이 함수를 포함한 총 6개의 집합과 5개의 함수를 요소로 갖는 C-DEVS formalism은 아래와 같다.

C-DEVS = <X, Y, S, CS, CV, C, δ_int, δ_ext, δ_con, λ, ta>

· X : 이산사건 입력 집합

· Y : 이산사건 출력 집합

· S : 일련의 이산사건 상태의 집합

· CS : 조건분기상태 집합

· CV : 조건변수집합

· C : n-dimensional 조건공간집합 (n = #(CV))

·δ_int : S → S U CS 내부 상태 전이 함수

·δ_ext : Q×X → S 외부 상태 전이 함수

Q = {(s, e) | s ∈ S, 0 ≤ e ≤ ta(s)} : total state of M

·δ_con : CS×P(C) → S 조건적 상태 전이 함수

P (C) : power set of C

· λ : S → Y : 출력 함수

· ta : S → R[0,∞] : 시간 진행 함수

Classic DEVS Atomic 모델은 네 개의 함수를 가지고 있는데, 확장된 C-DEVS Atomic 모델에서는 기존 네 개의 함수에 추가하여 ‘조건적 상태 전이 함수 (δ_con)’를 가지고 있다. 확장된 C-DEVS Atomic 모델에서 조건적 상태 전이함수(δ_con)가 “외부의 간섭 없이 스스로 상황변화를 인지”하는 자율제어시스템을 효과적으로 표현하게 해주는데 핵심적 역할을 수행한다. 조건적 상태 전이 함수(δ_con)의 치역은 Sequential states set(S)이며, 정의 구역은 조건분기상태집합 (CS)와 조건공간집합의 멱집합 (P(C): power ste of C)의 곱집합 (CS×P(C))으로 주어진다. 조건공간집합(C)은 n개의 조건변수의 조합으로 이루어진 n-dimensional space이다. 이러한 조건공간집합의 멱집합(P(C))은 자율제어시스템이 가질 수 있는 모든 조건의 전체집합이라고 볼 수 있다. 즉 조건적 상태 전이 함수 (δ_con)는 특정 조건 분기상태(CS)에서 자율제어시스템의 내부적 조건 (P(C))에 따라서 자유롭게 상태전이를 정의할 수 있게 해주는 것이다. 예제를 통한 더 자세한 설명을 위해, 다음 장에서 제안된 C-DEVS formalism을 이용하여 실제로 USV를 모델링한 예를 설명하고자 한다.

본 논문에서 제안된 C-DEVS formalism을 이용하여 대표적인 자율제어시스템인 무인 수상정 (Unmanned Surface Vehicle) 모델을 작성하여 시뮬레이션에 활용하였다. 설명을 돕기 위하여 앞서 예를 들었던 시나리오에 대하여 모델을 구축하고자 한다. USV는 특정 출발지점 P(P_X,P_Y,P_Z)에서 출발신호를 받으면 목적지인 T(T_X,T_Y,T_Z)지점까지 이동한 후에 멈추는 것이다. Classic DEVS formalism으로 이를 표현하기 위해서는 두 가지 방법을 생각할 수 있다. 첫 번째는 Classic DEVS formalism의 내부 상태 전이 함수(δ_int)로 표현하는 것이고, 두 번째는 조건을 고려하여 Sequential states set을 세분화하는 것이다.

첫 번째로 Figure 3에 보여 지는 것과 같이, Classic DEVS formalism의 내부 상태 전이 함수(δ_int)로 이를 표현하기 위해서는 USV가 목적지에 도착하는데 걸리는 시간(ta(Move))을 미리 알고 있다는 가정이 전제되어야 한다. 그러나 일반적으로 USV의 기동 시뮬레이션은 변화하는 자연환경(파고, 풍속, 풍향등)과 USV의 기동 성능을 고려하여 일정 시간 간격(delta_t)으로 위치를 update하는 방식으로 진행하므로, 목적지에 도착하는 시간을 미리 알고 있다는 가정은 성립되지 못한다. 두 번째로 Classic DEVS formalism의 내부 상태 전이 함수(δ_int)를 활용하지 않고 Sequential states set을 세분화함으로써 이러한 어려움을 피하는 방안을 고려해 볼 수도 있다. 하지만 이 경우에는 조건 분화의 개수 많아짐에 따라 State explosion 문제에 직면하게 되어 역시 용이하지 않다.

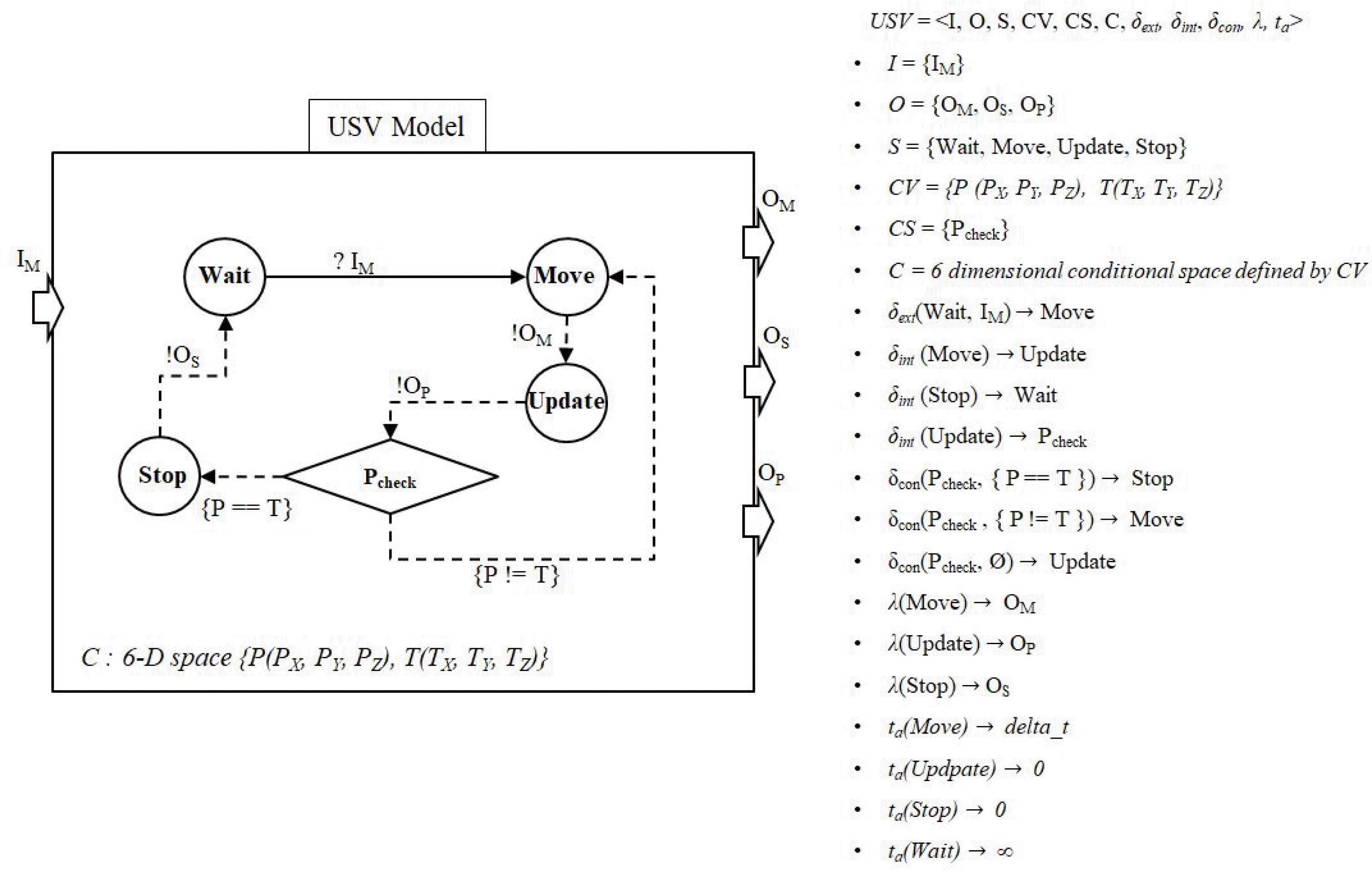
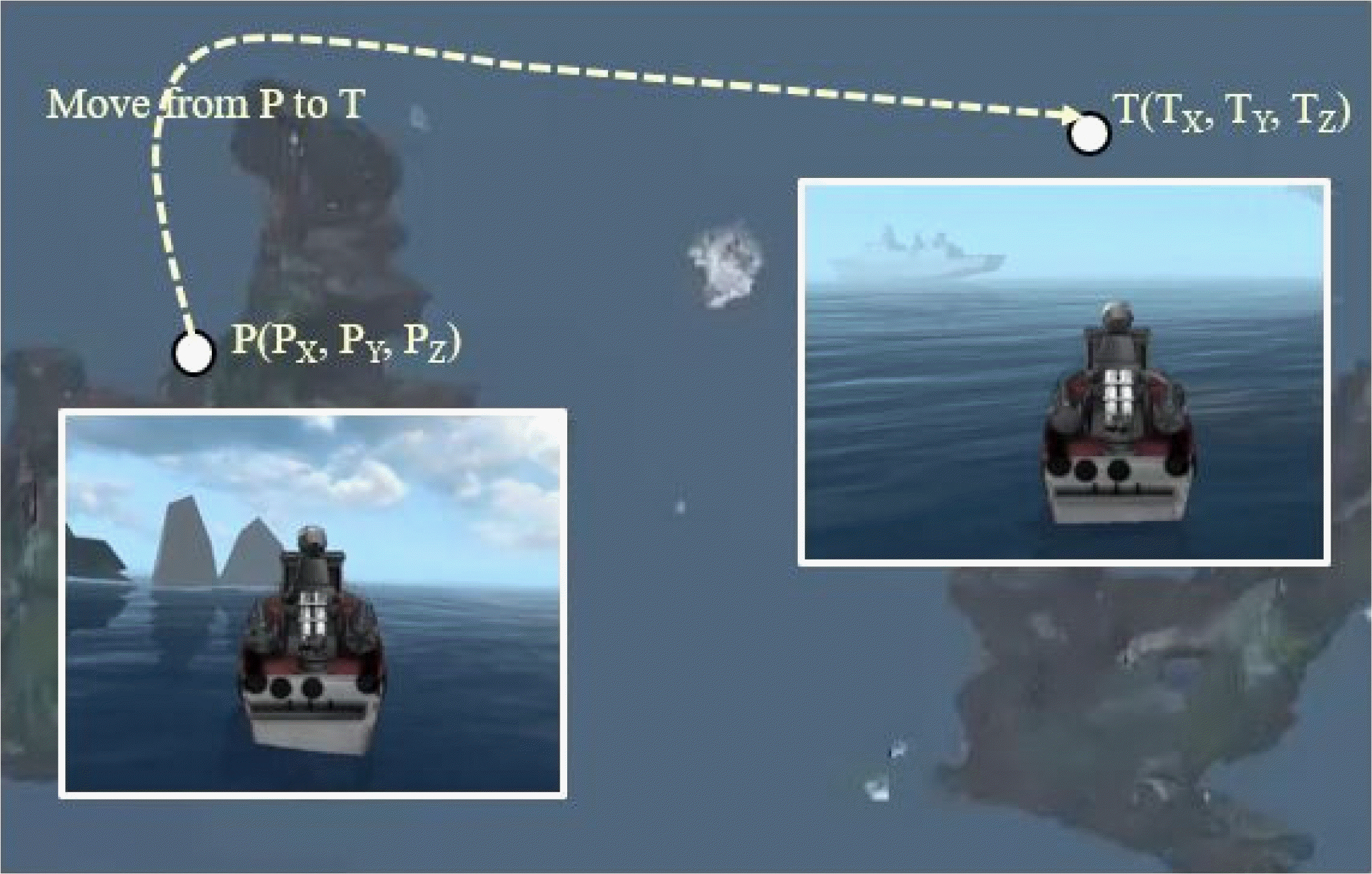
Figure 4는 Classic DEVS formalism을 확장함으로써 개발된 C-DEVS formalism 을 이용하여 USV 모델을 구축한 사례를 보여주고 있다. 구축된 USV 모델의 조건공간집합 (C)는 여섯 개의 실수 (PX,PY,PZ,TX,TY,TZ)로 정의된된 6-dimensional space가 된다. 일정 시간 간격으로 위치를 update 하면서 조건분기상태 (Pcheck)에서 목적지(TX,TY,TZ)에 도착했는지 여부를 감시한다. 만약 목적지에 도착하게 되면 이를 스스로 감지하여 정지하고 대기하도록 모델링 되어 있다. 확장된 C-DEVS formalism에서는 목적지에 도착하는데 소요되는 시간을 미리 알고 있지 못해도 상관 없으며, 조건분기상태와 조건공간집합을 도입함으로써 State explosion 문제도 피할 수 있다. 이러한 C-DEVS formalism의 검증을 위해 USV Simulator를 구현하였으며 Figure 5는 USV 기동 시뮬레이션을 보여주고 있다.

최근 국방분야에서는 미래전투체계 (FCS: Future Combat System) 개념이 많은 주목을 받고 있으며, FCS는 무인 수상정 (Unmanned Surface Vehicle), 무인 비행기 (Unmanned Aerial Vehicle)등 다양한 자율제어시스템(Autonomous Control System)을 포함하고 있다. 일반적으로 자율제어무기체계는 외부의 간섭을 최소로 하고 스스로 상황을 인지하여 임무를 수행하는 고가의 시스템이며, 효과적인 도입 및 배치를 위해서는 사전에 다양한 상황에서의 시뮬레이션을 통해 소요 군이 원하는 목표수준의 효과를 달성 할 수 있는지를 검증하는 것이 매우 중요하다고 할 수 있다.

시뮬레이션 결과의 정합성은 모델의 정합성에 달려 있으므로, 정합성 높은 모델을 구축하는 것이 매우 중요한데, 기존에 다양한 모델링 방법론이 존재하지만, 특히 Classic DEVS formalism은 객체지향적이며 계층구조를 효과적으로 지원함으로써 다양한 분야에서 정합성 높은 시뮬레이션 모델 구축에 활발히 사용되었다. 특히 제조분야와 국방분야에서 다양한 목적을 위해 성공적으로 잘 활용된 바 있다. 하지만 “외부의 간섭 없이 스스로 상황변화를 인지”하는 자율제어시스템을 표현하는 데에는 어려움이 있을 수 있다. 기존 DEVS Atomic 모델에서 상태 전이를 일으키는 함수는 외부 상태 전이 함수(δ_ext)와 내부 상태 전이 함수(δ_int)의 두 가지가 있다. 자율제어시스템이 스스로 상황변화를 인지하여 상태 전이를 일으키는 것은 내부 상태 전이 함수(δ_int)를 사용하여 표현하여야 하는데, 이는 기존 내부 상태 전이 함수(δ_int)만으로 표현하기에는 어려움이 있다. 기존 내부 상태 전이 함수(δ_int)는 정해진 시간이 경과하면 상태변화를 일으킨다. 이를 바꾸어 말하면 기존 내부 상태 전이 함수(δ_int)는 내적인 상태변화에 소요되는 시간을 이미 알고 있다고 가정하고 있다는 것이다. 하지만 자율제어시스템의 경우 이러한 가정이 성립되지 않는 경우가 많다. 주어진 자연환경의 변화를 실시간으로 고려하여 임무를 수행하는 자율제어시스템의 경우 특정 임무를 수행하는데 걸리는 시간을 미리 알 수가 없기 때문이다.

이러한 어려움을 극복하기 위하여, 본 연구에서는 자율적인 논리와 행위를 모델링 할 수 있도록 조건분기 상태(CS, Conditional State)와 조건변수(CV, Conditional Variable) 개념을 차용하여 classic DEVS formalism을 확장하여 C-DEVS formalism을 개발하였다. 제안된 C-DEVS formalism은 조건변수(CV)를 이용하여 조건분기 상태(CS)의 상태전이를 정의하고, 이를 통해 자율제어시스템의 자율적인 논리 및 행위를 효과적으로 모델링 할 수 있게 한다. Classic DEVS formalism에서는 상태 전이는 외부에 의한 사건 발생이나 내부적인 시간흐름에 의해서만 상태 전이가 이루어지지만, C-DEVS formalism에서는 현재의 상태에서 주어진 조건에 대한 판단으로 상태의 전이가 일어날 수 있으며, 조건에 의해 전이되는 상태도 달라질 수 있다. 마지막으로 논문에서 제안된 C-DEVS formalism의 유용성을 검증하기 위해 USV 모델을 구축하였으며 기동 시뮬레이션을 수행하였다.