다음은 문제 설명을 위한 기호이다.

<Indices>

i : order index i=1,…,n

j : stage index j=1,…,m

k_j : machine index at each stage, k=1,…, K_j

d: day index d=1, …, r (planning horizon = r days)

l: shift index l=1, 2

<Parameters>

α : OEM 품번을 우선적으로 할당하기 위한 가중치

β: 기계 평균 가동률

β_i,j : i 주문이 j스테이지에서 가공해야 하면 1, 아니면 0

γ_i,j,k : i 주문이 j스테이지 k 기계에서 가공할 수 있으면 1, 아니면 0

δ_i,j,k : i 주문의 j스테이지 k 기계에서의 가공 시간,

W_l: l 시프트에서의 근무 시간(작업 가능 시간)

C_k,d,l : k 기계를 d 일 l시프트에서 사용 가능하면 1, 아니면 0

D_i: i 주문의 납기일

본 연구에서 다루는 HFS는 다음과 같은 특징과 가정을 갖는다.

1) 주문 및 작업 내역은 계획 초기에 알려져 있다. (동적 주문 도착과 긴급 생산은 고려하지 않는다.)

2) 각 작업(주문 또는 제품)의 생산 순서는 공정마다 한 개 이상의 병렬 기계가 존재하는 흐름공정과 같이 한 방향으로 진행되나, 제품의 유형에 따라 특정 단계는 거치지 않을 수도 있다.

3) 공정 간 버퍼 사이즈는 무한하며, 각 기계에서의 작업시간은 상수로(deterministic) 알려져 있다.

4) 각 작업은 로트(lot) 단위로 진행되는데, 하나의 기계는 동시에 하나의 로트만 가공할 수 있으며, 나머지 작업들은 재공 재고(WIP)으로서 각 단계 중간에서 대기하게 되고, 하나의 기계가 가용하게 되면 대기 중인 작업 중 주어진 순서에 따라 투입된다. 공정 간 이동거리나 이동시간은 무시한다.

5) 순서 의존적 셋업 시간: 각 작업 간에는 제품의 종류에 따라 셋업 시간이 발생한다. 셋업 시간은 선후 작업의 유사도에 따라 달라진다.

6) 작업 우선순위: 각 주문은 2가지 수준의 우선순위(OEM = 높은 우선순위, AS = 낮은 우선순위)와 납기일이 주어진다.

7) 작업 일정에 따른 가용한 기계의 변화: 작업자는 2교대로 작업하며, 이에 따라 날짜 및 shift, 잔업 수행 등의 사유에 의해 일정별로 사용 가능한 기계가 달라질 수 있다. 예를 들어, 여러 가지 현실적인 제약에 의해 주간과 야간작업자 수가(ex., 주간 6명, 야간 3명) 다르므로, 가용한 기계의 종류 및 대수도 작업자 일정에 따라 달라질 수 있다.

8) 각 스테이지는 이종 병렬 기계로 이뤄져 있으며, 일부 작업은 특정 기계 또는 특정 기계 군에서만 가공 가능(DEDicated machine)하고, 기계에 따라 가공 소요시간은 달라질 수 있다. (이하 DED)

위에서 제시한 가정 중, 1) ~ 5)는 HFS 시스템에서 보편적인 사항이나, 6) ~ 8)은 본 연구에서 다루는 특수한 고려 사항에 해당한다. 특히, 8) 조건을 가진 HFS에서는 각 오더마다 갈 수 있는 기계, 공정이 다르기 때문에 오더의 투입 순서에 따라 후속 공정의 상황이 크게 바뀌므로 첫 공정의 투입이 가장 중요하다. 또한, 동종 병렬 기계(identical parallel machine)의 경우와 달리, 이종 병렬 기계 하에서 DED 문제의 경우에는 각 스테이지에서 기계별 부하를 고려하여야 한다. 특정 기계에만 작업이 가능한 품번들만 생산되면 해당 스테이지가 병목이 되기 때문에, 각 스테이지의 설비들이 모두 작업 가능하도록 workload balancing을 고려하여야 한다.

고려하는 제조 시스템에서 생산물량은 미리 지정되어 있고, 주문은 OEM과 AS로 두 가지 우선순위를 가지며, 특정 제품의 종류에 따라 생산 가능한 경로, 수량, 납기 등의 정보를 갖고 있으며, 이런 정보는 생산계획 시 모두 알려져 있다고 가정한다. 실제 사례에서는 ERP 시스템과 연계하여 BOM 정보로부터 MIP 모델 생성 시 자동화하여 추출할 수 있다. 실제 각 공정에서는 선후 작업의 품번에 따라 그 셋업 타임을 가지는데, 위에 제시한 수리 모형에서는 순서-의존적인 셋업 타임은 고려하고 있지 않고, 대신 기계의 평균 가동률을 생산 가능 시간에 곱해줌으로써 셋업타임을 위한 여유시간을 반영하고 있다. 모든 제품의 첫 공정은 1번 스테이지이며, 중간에 특정 스테이지는 건너뛸 수 있으나, 그 방향성인 가공 순서는 모두 동일하다. 실제 하나의 주문이 여러 로트(Lot)로 나뉘어 가공될 수 있으나, 본 연구에서는 하나의 주문은 하나의 로트로 가공되나, 로트 사이즈는 주문량에 따라 다를 수 있다고 가정한다.

생산 일정 계획 문제에서는 용도에 따라 다양한 목적함수가 사용될 수 있다. 이 중 흔히 많이 사용되는 것으로 완료 시간(maximum/total/average completion time), 흐름 시간(maximum/total.average flow time), maximum/total/average lateness, maximum/total/average tardiness, maximum/total/average earliness, 납기 지연된 로트 수 등이 있는데, 그중 아래에 제시되는 2가지를 가장 보편적으로 고려할 수 있다.

식(1)은 로트 별 가중치(w_i)를 고려한 납기지연(tardiness)의 합을, 식(2)은 최대 완료 시간을 최소화하는 것이고 것이다. 본 연구에서는 이 중 식(1)에 표현된 납기지연을 주 성능지표로 삼고, 사례연구에서는 참고적으로 식(2)의 완료 시간을 제시한다.

생산계획과 스케줄링을 한 번에 수리적으로 모델링 할 수는 있겠으나 문제의 클래스가 NP-hard임을 고려할 때, B&B 방법 등을 이용하지 않고 MIP 모형을 직접적으로 사용하면 실용적인 문제에서는 그 최적해를 찾는 것은 어렵다. 본 연구에서는 수리 모형을 기계 별 부하 평준화를 고려하여, 납기를 최소화하기 위한 Bin Packing 모형의 변형을 제안한다. 경우에 따라서는 시간이 많이 걸릴 수 있겠으나, 이런 경우 시간 제약을 주고 구해진 현재 최적해를 2단계 생산 스케줄링을 위한 입력 자료로 사용한다.

본 연구에서 고려하는 1단계 작업 할당 문제를 혼합 정수계획법 모형으로 표현하면 다음과 같다.

<Decision Variables>

t_i: i 로트의 납기지연,

x_i,j,k,d : i 로트가 j 스테이지의 k 기계에서 d 일에 작업하면 1, 아니면 0

s.t.

식(3)의 목적함수는 OEM Tardiness와 AS Tardiness의 가중합을 최소화하는 것을 나타내는데, 첫 항목은 총 OEM 오더들의 총 납기지연을, 두 번째 항목은 AS 오더들의 총 납기지연을 각각 나타낸다. 두 납기지연은 가중치에 의해 조정된다. 식(4)는 각 작업은 한 스테이지에서 가공 가능한 기계에 한에 한 번만 할당되어야 한다는 제약을 표현한다. 식(5)은 기계 별, 일 별 capacity 제약을 표현한다. 좌변에 표현된 기계 k에 d일에 할당된 작업 시간 합은 우변에 표현된 각 기계(k)가 d일에 총 가능한 작업시간보다 같거나 작아야 한다. 식(6)는 작업 순서에 따른 precedence relation과 선후 작업의 시작 시간 제약을 표현한다. 좌변의 첫 번째 수식은 선행하는 스테이지 j에서의 작업일 d에 작업시간을 더한 값을 나타내고, 두 번째 부분은 후속 스테이지 j+1에서의 작업일을 나타내는데, 그 값은 첫 번째 항의 값보다 같거나 크다. 식(7)는 각 오더의 납기지연(t_i)를 계산하는 표현식이다. 식(8)은 결정 변수의 이진정수조건, 식(9)은 결정변수가 비음의 실수임을 나타낸다.

참고로 수리 모형에서 그리스문자로 표기된 모수들은 공정과 제품의 기준정보에 의해서 추출되는 상수 값이고, 영문 대문자로 표기된 모수들은 오더 정보와 작업자 일정 계획 등에 따라 생산계획 수립 시 변경되는 상수 값을 나타낸다.

1단계의 결과는 각 로트가 어느 기계에서 가공될지 모두 결정하지만, 그 결과를 2단계에 투입될 때는 3가지 방식으로 사용될 수 있다. Case 1은 모든 스테이지에서 각 로트에 특정 기계를 지정, Case 2는 첫 번째 스테이지에서만 특정 기계를 지정, Case 3은 결과를 바탕으로 일별 투입 순서만 설정하는 것이다. 이에 대한 논의는 5장 사례 연구에서 자세히 설명된다.

공정 중에는 두 가지 경우의 선택 상황이 발생한다. 첫 번째는 job 디스패칭 상황으로, 한 기계에서 가공이 완료된 로트는 다음 스테이지에 도착할 때, 해당 스테이지의 기계 중 해당 품번의 로트를 가공할 수 있는 기계들이 모두 가공 중이면 그 로트는 해당 스테이지에서 대기하게 되고, 가공 가능한 기계가 가용하게 될 때, 그 가공을 마친 기계는 대기 중인 로트 중에서 선택을 하게 되는데, 이때 미리 지정된 디스패칭 규칙이 적용된다. 본 연구에서는 납기지연을 최소화하기 위해 널리 사용되는 EDD(Earliest Due Date), MDD(Modified Due Date), MST(Minimum Slack Time) 규칙과 더불어 문제의 특성을 고려한 몇 가지 디스패칭 규칙을 제안한다. 두 번째는 기계 디스패칭 상황으로, 하나의 로트가 어느 스테이지에 도착할 때, 2개 이상의 기계가 가용하면 그 로트는 기계 중 하나를 선택해야 한다. 이때는 앞서 제시한 EDD 등의 디스패칭 규칙을 사용할 수 없으므로, 기계 선택과 관련된 선택 규칙이 필요하다.

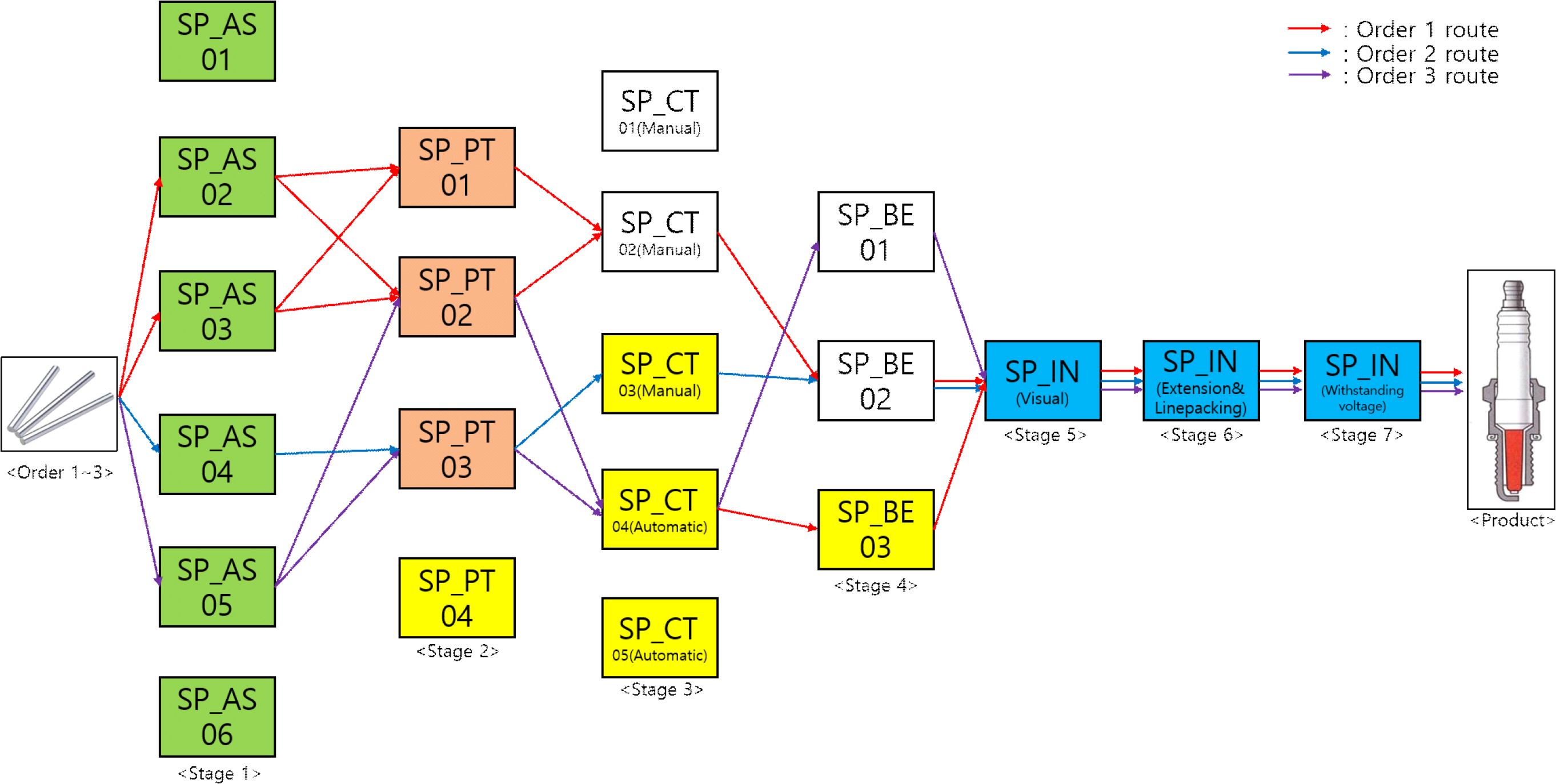
본 연구에서 실험한 대상 기업은 국내 자동차 제조업의 1차 협력업체로 자동차 엔진용 스파크 플러그 제조업체이다. 스파크 플러그 제조 공정은 크게 CF(냉간단조) 공정, CM(선반가공 및 용접) 공정, 도금 공정, 그리고 조립 및 검사 공정(SAS)으로 이루어져 있으며, 본 연구에서는 조립 및 검사 공정만을 고려한다. 조립공정은 7 스테이지로 이뤄져 있으며, 이종 병렬 기계가 배치된 공정은 전반부 4개 공정이다. 첫 공정은 자동조립기 공정으로 6기가 있으며, 주간 6기, 야간 3기만 가동된다. 두 번째 공정은 용접 공정, 세 번째는 절단, 네 번째는 굽힘 공정이고, 외관 검사, 중축 및 선 패킹 검사, 내전압 검사 공정이 이어진다. 각 공정별 기계 대수는 Figure 2를 참조할 수 있다. Figure 2는 또한 어떤 3개 주문이 생산 가능한 경로(현업에서는 생산 버전이라 함)의 예시를 보여주고 있다. 예를 들어, 첫 번째 스테이지의 이종 병렬 기계 중, 주문 1 로트는 2, 6번 기계에서 가공이 가능하며 주문 2는 4번 기계에서, 주문 3은 3번 기계에 각각 가공될 수 있다. 두 번째 스테이지에서 주문 1은 1, 2번 기계에서, 주문 2는 3번 기계에서, 주문 3은 2, 3번 기계에서 각각 가공될 수 있다. 이처럼 각 오더는 각 스테이지별로 가공 가능한 기계가 다르다.

이 생산 라인에서는 총 370여 종의 제품을 생산 가능하나, 실질적으로는 145개 품종을 생산하고 있으며, 주당 평균 100여 개의 주문을 생산하고 있다. 각 주문에는 품번에 따라 OEM 용 생산과 AS 용 생산으로 나눠지며, 업종의 특성상 OEM용 생산의 납기는 우선적으로 지켜야 한다. 로트 사이즈는 5520개이며, 각 로트는 최대 7개 스테이지에서 가공되어야 한다.

대상 기업의 2017년 전반기 6개월 실제 생산 자료로부터 OEM과 AS용 주문의 비율을 적용하여 가상의 주문 목록을 만들었다. 이 주문 목록은 주간 생산 기준 88개의 로트로 구성되어 있으며, 총 30개의 주문 목록을 생성하여 실험하였다. 30개의 주문 목록별로 납기일을 2가지 버전(납기일 기본, 기본 + 1일)으로 총 60개 실험 데이터를 생성하였다.

MILP 모형에서 기계 평균 가동률(ρ)는 실제 가동률을 감안하여 85%로 설정하였으며, OEM 주문의 납기지연에 대한 가중치(α)는 0.9, 디스패칭 규칙의 가중치는 w₁ = 10³, w₂ = 10², w₃ = 10, w₄ = 1로 실무자와의 협의 하에 결정하였다. 이는 각각의 규칙을 순서대로 우선 적용하되, 동률 발생 시 tie-break 규칙으로 이하의 디스패칭 규칙을 사용한다는 것을 뜻한다.

1단계 생산계획을 위한 수리 모형은 Excel add-in 소프트웨어인 Solver Foundation2.0과 Microsoft OML을 이용하여 모델링 되었고, 상용 MILP Solver 중 가장 빠른 것으로 알려진 Gurobi 7.5.2를 이용하였다(Amsterdam Optimization Modeling Group LLC, 2009; Campbell and Nikoukhah, 2018; Mittelmann, 2017). 2단계 생산 일정 계획 수립을 위해 해당 공정은 Rockwell Software의 Arena® ver.14.7로 모델링 하였고, 모든 실험은 인텔 i7 (2.4GHz) CPU, 메모리 8GB가 설치된 PC를 이용하여 실시하였으며, 모든 실험에서 30분 내에 주어진 모형의 해를 도출하였다.

1단계에서 나온 결과가 2단계에 투입될 때는 다음과 같이 4가지 방식으로 사용될 수 있다.

1) Dispatching Only: 디스패칭 규칙만 사용(1단계 사용하지 않음)

2) Priority +Dispatching: 1단계 결과를 바탕으로 우선순위만 설정하고 디스패칭 규칙 적용

3) Stage 1 + Dispatching: 첫 번째 스테이지의 기계만 1단계 결과를 활용하여 특정 기계 지정

4) All: 1단계 결과를 모든 스테이지에서 적용하고, 보조적으로 디스패칭 규칙 사용

첫 번째 Dispatching Only는 제안된 방법을 사용하지 않고 전통적인 디스패칭 규칙만을 사용하는 것이고, 네 번째는 제안된 방법이고, 두 번째와 세 번째는 그 중간 수준에서 섞어 사용하는 방법이다. 아래 Table 1은 위의 4가지 실험 조건에 따른 시뮬레이션 결과 값의 평균을 보여준다. 전체 평균으로 보면, 제안된 방법론을 적극적으로 사용할수록 해의 성능이 낮아지는 것으로 보인다. 실제 All 방법이 극단적으로 나쁜 성능을 보이는 것은 각 스테이지에서 기계 디스패칭 규칙을 전혀 사용할 수 없기 때문에 가공 가능한 유휴 기계가 있어도 할당된 기계가 가용할 때까지 버퍼에서 대기를 하게 되기 때문이다. 그러나 실제 시뮬레이션 기반의 의사결정에서는 다양한 실험 결과를 활용하여 최선의 선택을 할 수 있다.

Table 2는 각 방법별로 60회의 실험에서 OEM tardiness가 작은 등수의 요약한 것이다. 총 60회의 실험 중 Dispatching Only가 34회 가장 좋은 결과를 보이긴 하나, Priority + Dispatching 조합 방법과 Stage 1 + Dispatching 조합 방법도 역시 각각 13회와 18회 가장 좋은 해를 가진다. 1위와 2위의 총개수가 각각 65회와 63회로 실험 횟수인 60회보다 많은 것은 동률이 있었기 때문이다.

실험 결과를 볼 때, All 조합 방법은 위에 설명한 대로 기계 디스패칭 규칙을 사용할 수 없어서 항상 나쁜 결과를 보이지만, 나머지 세 가지 방법은 항상 우위를 점하는 방법은 존재하지 않으므로, 3가지 방법으로 모두 실험 후 최선의 결과를 선택하면 항상 기존의 디스패칭 규칙만 사용할 때보다 같거나 나은 결과를 보장하게 된다. 이렇게 Dispatching Only 방법을 포함한 3가지 방법을 모두 사용하고 최선의 방법을 선택할 경우, OEM Tardiness를 기준으로 총 60회의 실험 중 26회에서 1단계 결과를 활용할 경우 더 나은 결과를 보이며, OEM Tardiness 평균은 32.6으로 Dispatching Only에 비해 4.1% 감소함을 알 수 있다. 1단계 수리 모형의 결과를 활용하여 Dispatching Only 방법보다 작은 OEM Tardiness를 보이는 26개 사례만을 추출하여 3가지 조합 방법의 평균 OEM Tardiness를 구하면 Table 3과 같다. 이 26개 사례만을 보면 조합된 방법을 사용할 때, 평균 OEM Tardiness는 9.2% 감소한다. All 방법을 제외한 모든 조합 방법에서 Makespan은 유의미한 차이를 보이지 않았다.