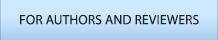1. 서 론
육/해상 플랜트 조선기자재 산업에서 저온용 후판의 용접작업은 압력용기 제조업 등에서 빈번하게 실시되며 중요한 공정 중 하나이다. 최근 LPG의 수요 증가로 인하여 –50℃이하 온도에서 내충격성과 기계적 성질 유지가 가능하게 하는 용접법이 필요하게 되었으며, 이러한 충격강도를 확보할 수 있는 용접 조건 및 방법 연구가 진행되고 있다(Jung, 2011). 또한 전 세계적으로 연료 운송비 절감을 위해 천연 가스 생산 지역과 소비 지역을 원거리 파이프 등의 직접 연결이 진행되고 있으며, 특히 알래스카 및 시베리아와 같은 저온 건설 현장의 경우 운송 파이프 및 연결 부위의 저온 충격 강도가 반드시 요구된다(An et al. 2014). 이러한 저온에서 용접부의 기계적 시험 결과인 충격 강도 등을 만족시키기 위한 다양한 연구가 제시되고 있지만, 대부분이 용접 작업조건 확보에만 초점을 맞추고 있는 실정이다. 따라서 자동 용접의 생산성을 함께 고려한 최적 용접 조건을 확보할 수 있는 방법 마련이 반드시 필요하다고 할 것이다.
이에 본 연구에서는 후판의 용접 방법 중 가장 널리 사용되고 있으며, 용접기술자에 의한 용접 품질의 차이를 최소화할 수 있는 Submerged Arc Welding(SAW)을 연구대상으로 하여 저온에서의 충격 강도를 만족함과 동시에 생산성을 최대화할 수 있는 용접조건을 도출하고자 한다. 시험편의 제작 및 시험은 ASME SA370의 규정 및 표준에 따라 수행되었으며, 시편 제작 및 충격 시험 등의 모든 시험 결과는 절차검정기록서(Qualification Test Record, PQR)에 따라 상세하게 기록하였다. 그리고 실험 횟수의 최소화와 실험 결과의 신뢰성 최대화를 위하여 맞춤형 단계적인 실험계획법 적용방안을 마련하였다. 먼저, 주요 인자를 선별하여 특성화 단계를 위한 완전요인실험을 중심점을 포함하여 설계하여 제시하였고, 실험 결과를 바탕으로 입력변수의 유의성 및 범위에 대한 타당성 분석을 수행하였다. 그리고 분석 결과를 바탕으로 다음 단계인 최적화 실험을 반응표면법(Response Surface Methodology, RSM) 중에 하나인 중심합성법(Central Composite Design, CCD)을 적용한 설계 방법을 제시하였다. 특히, 분산분석(Analysis of variance, ANOVA) 결과를 바탕으로 CCD 방법 중 외접중심합성법(Central Composite Circumscribed design, CCC)과 면중심합성법(Central Composite Face-centered design, CCF)을 적용하기 위한 통계적 방법을 상세하게 제시하였다. 또한, 최적화 실험 결과를 바탕으로 저온 충격 강도와 용접 시간을 동시에 만족할 수 있는 다차원 디자인 스페이스(Design Space, DS)를 제시하였다. 아울러 보다 높은 통계학적 신뢰성을 확보하기 위하여 도출된 디자인 스페이스에 신뢰구간(Confidence Interval, CI)을 적용하여 안전가용영역(Safe Operating Space)과 허용가능범위(Normal Acceptable Range, NAR)를 제시하였다. 마지막으로 제안된 허용가능범위 및 최적 용접 조건에 대한 검증 및 재현성 실험을 수행하여 연구 결과의 유효성을 확인하였다. 본 연구에서 제안된 최적 용접 조건 및 가용영역을 바탕으로 작업 조건이 표준화되어 적절하게 관리되면 제품의 품질 및 생산성 향상에 크게 기여할 것이라 기대된다.
2. 이론적 배경 및 선행연구
2.1 SAW(Submerged Arc Welding)
SAW는 용접선의 표면에 입상의 피복제(flux)를 미리 산포하고, 내부에 용접 와이어를 연속적으로 공급하여 와이어 선단과 모재 사이에 아크(Arc)를 발생시켜 아크열에 의해 모재 및 와이어, 피복제를 용융시켜 접합하는 자동 용접 방법을 말한다(Lee, 2011). 아래 Figure 1에서 보는 바와 같이 아크를 입자 모양의 피복제로 보호하며 용접이 이루어지기 때문에 아크가 외부에 노출되지 않아 잠호 용접이라고도 한다. 녹아 들어가는 기점이 깊고 결함이 거의 생기지 않아 용접 이음부의 신뢰도가 높고 가스 발생량이 적어 청정한 환경을 유지할 수 있다는 장점이 있다.
저온에서의 SAW 용접 시 반드시 만족되어야 할 품질특성에는 인장강도, 연신율, 충격강도, 용접시간 등이 존재하며, 이 중 용접 품질에 가장 큰 영향을 미치는 특성은 충격강도이다. 충격강도는 용접 입열량에 많은 영향을 받게 되며, 용접 관련 국제 규격인 ASME SEC IX QW-409 (ASME, 2017)에서 제시하는 바와 같이 용접 입열량은 아래 식 (1)과 같이 계산된다.
2.2 단계적 실험계획법
실험계획법(Design of Experiment, DoE)은 입력변수와 출력변수간의 함수관계를 규명하는데 매우 효과적인 방법이며, 실험 횟수를 최소화하면서 가장 효율적으로 통계적 분석을 수행할 수 있는 방법이다. 특히, 아래 Figure 2에서 보는 바와 같이, 실험 횟수를 최소화하기 위해서는 단계적인 DoE(스크리닝, 특성화, 최적화)의 설계가 매우 중요하고, 입력변수의 수와 통계적 분석 결과에 따라 선택적으로 수행할 수 있다. 먼저, 스크리닝 단계는 실험의 초기 단계로 입력변수의 수가 많아 반응변수 및 목표 품질에 영향을 미치는 중요입력변수를 선별하기 위한 단계이고, 실험 횟수의 최소화를 위해서는 플라켓 버만 방법(Plackett-Burman Design, PBD) 혹은 부분요인배치법(Fractional Factorial Design, FFD)이 주로 사용된다. 스크리닝 단계 실험 결과를 바탕으로 주요입력변수가 선별되었다면, 선별된 입력변수에 대한 통계적 유의성의 평가와 동시에 실험 범위의 적절성을 평가할 수 있는 특성화 단계의 실험으로 완전요인실험(Factorial Design, FD) 방법이 주로 사용된다. 마지막으로 품질 특성을 만족시키기 위한 입력변수들의 최적 조합 및 디자인 스페이스(Design Space, DS)를 도출하기 위해 최적화 단계를 수행하게 되며, 이를 위해서는 반응표면법(Response Surface Methodology, RSM)이 널리 사용되고 있다. RSM의 경우, 주로 2차 모형(second-order model)의 다항 회귀를 사용하며, 중심점의 반복과 축점 등을 통하여 곡률효과 및 정밀한 최적해를 도출할 수 있는 장점을 가지고 있다. RSM의 회귀식은 아래 식 (2)와 같다.
RSM의 대표적인 방법으로 중심합성법(Central Composite Design, CCD)과 박스-벤킨법(Box-Behnken Design, BBD)이 있다. CCD의 경우, 실험점이 꼭지점, 축점, 중심점으로 구성되기 때문에 완전요인설계(꼭지점 및 일부 중심점)를 먼저 수행하여 입력변수의 유의성 및 실험 범위의 적절성을 판단하고, 범위가 적절하다고 판단될 경우 축점과 나머지 중심점을 추가하여 실험을 진행함으로써 단계적 실험이 가능하다는 장점이 있다. CCD를 이용한 단계적 실험 절차 및 실험점 구성을 아래 Figure 3와 같다.
그리고 실험계획법 (DoE)을 활용한 파라미터 설계와 관련된 연구로 Vining and Myers (1990)의 Dual response 개념의 최적화 방법과 함께 제시되었고, 이를 바탕으로 Lin and Tu (1995)는 Mean squared error기반의 개념을 제시하기도 하였으며, 그 이후 많은 연구들이 제시되어왔습니다 (Robinson et. al, 2004; Ho and Shin, 2018). 또한 공정개선에 관련된 연구로 Byun et al. (2014)는 실험계획법을 활용한 속경화 초전온 접착제 개발과 관련된 사례 연구를 제시하였고, Lee et al. (2015)는 실험계획법을 활용한 전자부분 최적운영조건과 관련된 사례 연구를 제시하기도 하였다.
2.3 디자인 스페이스(Design Space)
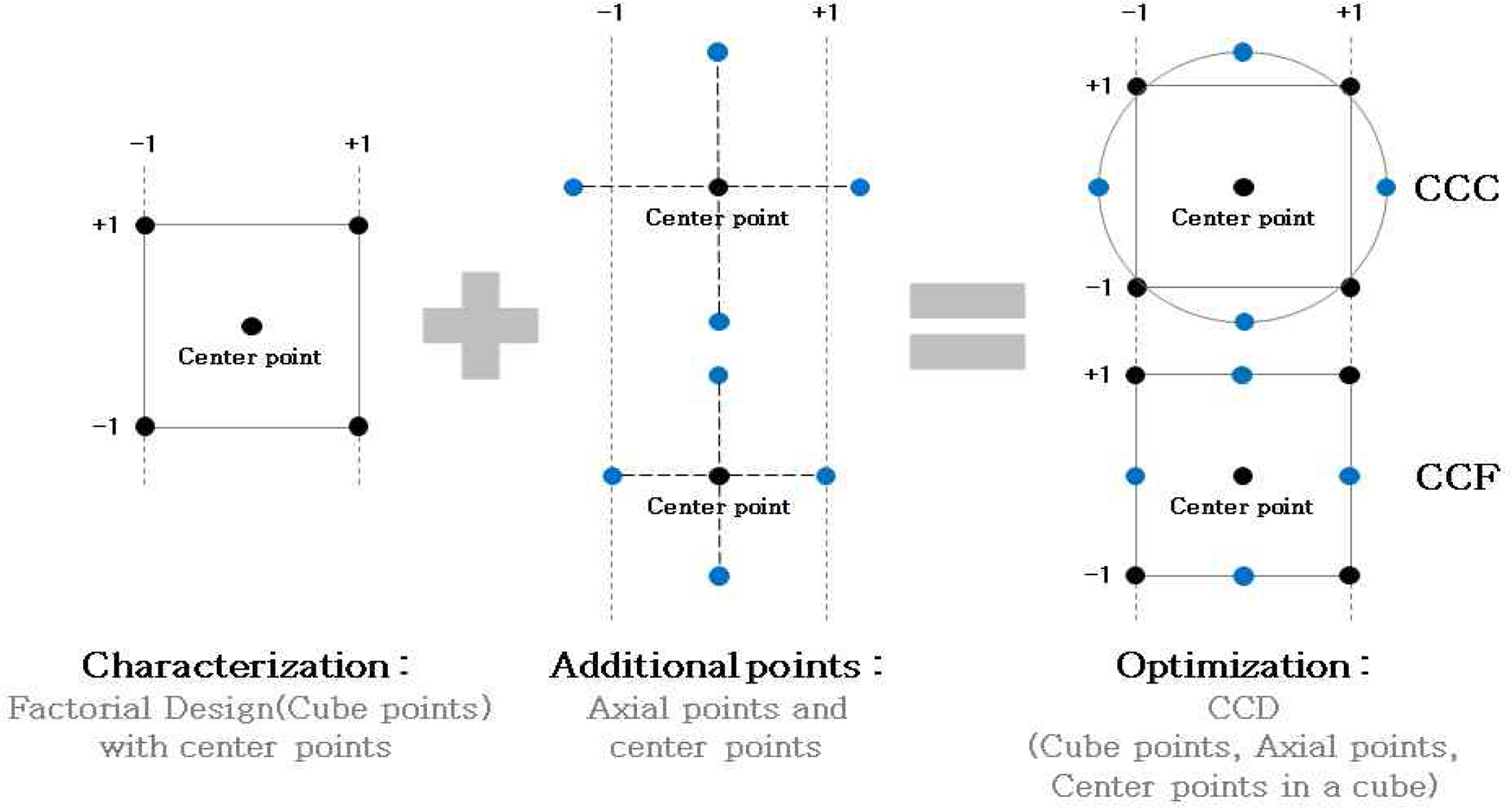
디자인 스페이스(Design Space, DS)는 품질 특성을 만족시키는 신뢰성 높은 통계적 설계 가능 영역을 의미하며, 디자인 스페이스 안에서의 변동은 목표 품질의 저하를 초래하지 않으며, 디자인 스페이스를 벗어나는 변동은 목표 품질의 손실을 발생시킬 수 있다 (ICH guideline, 2009; Xu et al., 2012; KFDA, 2016). 디자인 스페이스는 DoE 결과를 바탕으로 주요품질특성과 주요입력변수들 간에 함수관계를 도출하고, 도출된 함수가 목표 품질의 규격 상한(Upper specification limits, USL)과 규격 하한(Lower Specification limits, LSL)을 만족하는 영역으로 제시된다. 아래의 Figure 4에서 보는 바와 같이 실험을 설계한 영역을 Knowledge space라고 하고, 목표로 하는 품질의 기준을 만족할 수 있는 입력변수의 설계 가능영역을 Design Space라고 하며, 디자인 스페이스 내에서 보다 안전한 설계 영역을 Operating Space라고 정의할 수 있다.
그리고 두 개 이상의 반응변수가 존재할 경우, 아래 Figure 5에서 보는 바와 같이 반응변수와 입력변수의 함수관계는 등고선도 형태로 표현될 수 있으며, 두 반응변수의 등고선도를 중첩시켜 중첩등고선도를 도출할 수 있다. 아래 Figure 5의 오른쪽 그림은 두 품질특성의 중첩등고선도를 나타내고, 규격 상·하한을 동시에 만족하는 영역을 디자인 스페이스로 정의하고 있다(ICH guideline, 2009).
3. 연구 방법
3.1 시험편 제작
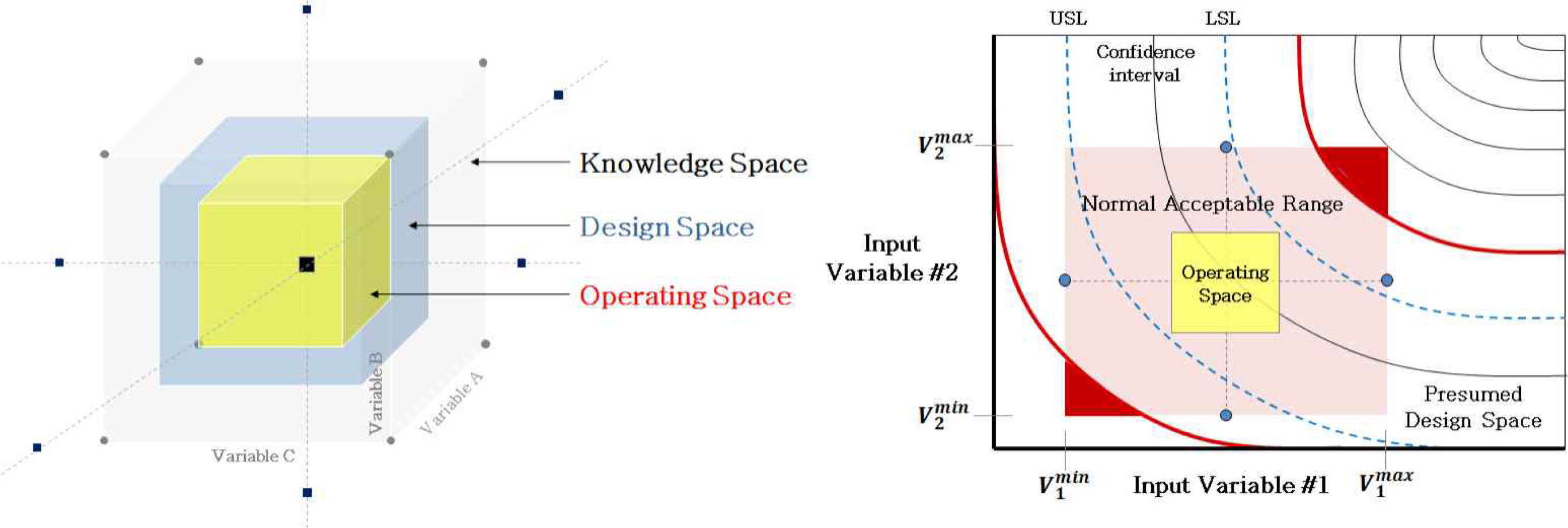
실험에 사용된 용접기는 Submerged Arc Welder(Idealarc DC1000, LT-7 Tractor/LINCOLN ELECTRIC)이며, 용접 시험편 모재(SA516 Gr.70N, 34mm) 및 용가재(AWS A5.17/ASME SFA5.17 F7A(P)6-EM12K)를 사용하였다. ASME-SA370 (ASME, 2017) 시험편 가공 표준에 따라서 저온용 후판 용접 시험편을 제작하였으며, 국제 용접 기준인 ASME-SA370 (ASME, 2017)과 ASME SEC VIII UG84 (ASME, 2017)에 따라 Test를 진행하였다. 실험 조건에 맞게 제작된 시편에서 아래의 Figure 6와 같이 인장시편 1개, WELD부 충격시편 3개, HAZ부 충격시편 3개를 제작하였다.
3.2 RSM(반응표면법)을 적용한 단계적 실험설계 및 분석방법
RSM의 적용은 주로 최적화 단계에서 이루어지며 2.2절에서 제시한 바와 같이 CCD와 BB가 널리 사용되고 있다. 본 연구에서는 두 가지 방법 중 CCD를 사용하여 실험 횟수를 최소화함과 동시에 정밀한 최적해를 도출할 수 있는 방안을 제시하고자 한다. 특히, 실험설계 후 모든 실험점을 랜덤하게 설계하여 적용하는 기존 CCD 적용방법과는 달리, 본 연구에서는 CCD를 두 단계의 실험(특성화 단계 및 최적화 단계)으로 나누어 설계하였다. 그리고 두 단계의 실험에 필요한 실험 방법 및 절차를 구체적으로 마련하여 아래의 7단계 알고리즘으로 제시하였다.
Step 1. 반응변수 정의 및 주요입력변수 선별
- 반응변수의 목표 품질 정의
- 주요입력변수 선별 및 실험 범위 설정
Step 2. 특성화 단계 실험 설계 및 결과 분석
- 2수준 FD에 중심점(Center point) 추가하여 실험 설계
- 분산분석을 통해 선정된 주요입력변수의 유의성 및 실험 범위의 적절성 확인
- 모형의 p-value < 0.05 (추정된 회귀 모형이 유의하다고 판단함): 축점 및 중심점 추가하여 Go to Step 3
- 모형의 p-value > 0.05 (추정된 회귀 모형이 유의하지 않다고 판단함):
Case 1. 입력변수의 재선정이 필요한 경우: Go to Step 1
Case 2. 실험의 범위가 적절하지 않을 경우: 실험 범위 재설정 후 Go to Step 2
Step 3. 최적화 단계 실험 설계 및 결과 분석
- CCD기반으로 실험 설계: Step 2 결과를 바탕으로 CCC 또는 CCF
※ 선정 기준: 모형의 p-value가 0에 가까울수록 CCF를 선정하고, 0.05에 가까울수록 CCC를 선정
- 분산분석을 통한 주효과/교호작용 파악 및 추정 회귀식 도출
※ 추정 회귀식: y ^ ( X ) = β ^ 0 + X T b ^ + X T B ^ X
- 모형의 p-value < 0.05 (추정된 회귀 모형이 유의하다고 판단함): Go to Step 4
- 모형의 p-value > 0.05 (추정된 회귀 모형이 유의하지 않다고 판단함):
Case 1. 입력변수의 재선정이 필요한 경우: Go to Step 1
Case 2. 실험의 범위가 적절하지 않을 경우: 실험 범위 재설정 후 Go to Step 2
Step 4. 디자인 스페이스 도출
- 고정된 입력변수의 수준(-1, 0, +1)에 따른 모든 경우의 디자인 스페이스 도출
- 도출된 디자인 스페이스를 바탕으로 2개의 주요입력변수 선정 (디자인 스페이스의 평가)
※ 선정 기준: 고정된 입력변수의 수준 변화에 따른 디자인 스페이스의 영역 변화가 큰 2개의 변수 선별
- 주요 2개 입력변수가 각 축에 고정된 디자인 스페이스 선정 (그 외 입력변수는 수준별로 고정): Go to Step 5
Step 5. 신뢰구간을 적용한 다차원의 디자인 스페이스 도출
- 선정된 디자인 스페이스를 모두 중첩하여 다차원의 디자인 스페이스 도출
- 안전한 가용영역 및 NAR을 도출하기 위해 다차원의 디자인 스페이스에 신뢰구간 적용: Go to Step 6
※ 신뢰구간(Confidence interval): y ^ ( X 0 ) - t α / 2 , n - p σ 2 X 0 T ( X T X ) - 1 X 0 ≤ μ y X 0 ≤ y ^ ( X 0 ) - t α / 2 , n - p σ 2 X 0 T ( X T X ) - 1 X 0
- 디자인 스페이스가 매우 좁거나 존재하지 않는 경우 (실험의 범위가 유의하지 않은 경우 발생): 실험 범위 재설정 후 Go to Step 2
Step 6. 안전가용영역 및 NAR 도출
- 신뢰구간이 적용된 다차원의 디자인 스페이스 내에서의 안전가용영역을 도출하고 그에 따른 NAR 도출
Step 7. 최적 조합 도출
- 안전가용영역 및 NAR 내에서의 품질특성을 가장 만족시키는 입력변수의 최적 조합 도출
Step 1에서 선정된 주요입력변수와 실험 범위에 대한 타당성을 입증하기 위해 Step 2의 특성화 단계 실험이 수행되며, 실험 결과를 바탕으로 분산분석을 수행하여 도출된 모형의 p-value를 통해 추후 진행될 Step 3의 최적화 단계 실험 방법이 결정된다. 이 때, p-value는 추정된 회귀 모형과 주효과 및 교호작용 등의 유의성을 검증하는 것으로, p-value가 유의수준(α, 일반적으로 α=0.05)보다 작으면 유의하다고 판단한다. 먼저, 모형이 유의(모형의 p-value≤ 0.05)한 경우 CCC 또는 CCF의 방법을 선택하여 최적화 단계의 실험을 수행할 수 있다. CCC가 CCF에 비해 실험 범위가 넓게 설정되기 때문에 입력변수의 변화에 따른 출력변수의 변화폭이 크다고 할 수 있으며, 그에 따른 p-value는 확률적으로 작아질 가능성이 크다. 따라서 CCC와 CCF의 선택에서는 특성화 단계(FD+중심점)의 분산분석 결과 모형의 p-value가 유의수준(0.05)에 근접할 경우는 범위가 넓은 CCC의 활용이 효과적이며, 반대로 모형의 p-value가 0에 가까운 경우는 범위가 좁은 CCF를 사용하여도 무방할 것이다. 다음으로, 모형이 유의하지 않은(모형의 p-value>0.05) 경우, 입력변수의 선별 또는 실험 범위의 설정이 잘 못 되었음을 의미한다. 따라서 입력변수를 재 선별하거나 실험의 범위를 재탐색해야하며, 변경된 입력변수 및 실험의 범위를 바탕으로 다시 특성화 단계부터 최적화 단계까지의 실험을 수행하여야 한다.
3.3 다차원의 디자인 스페이스 및 안전가용영역
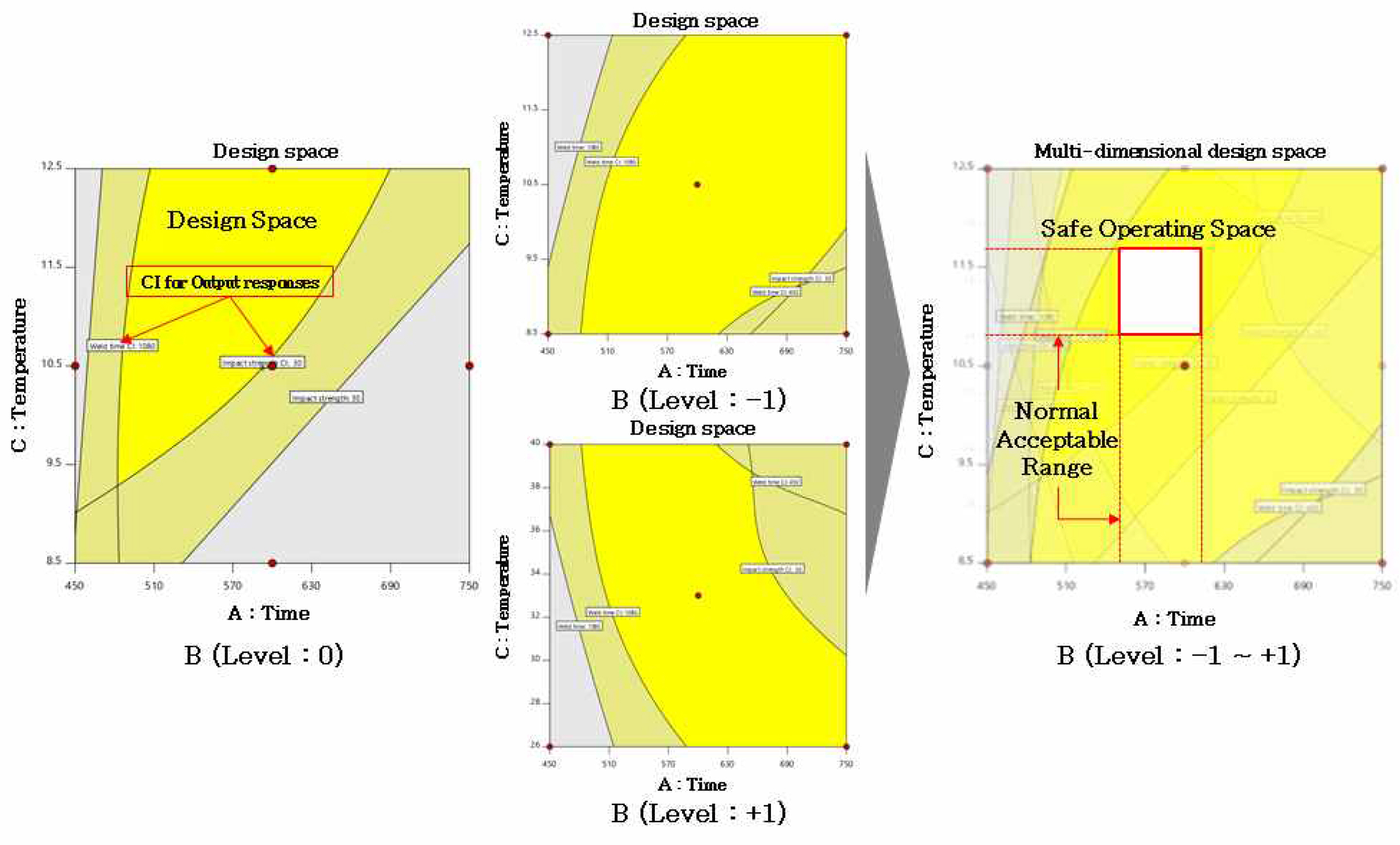
디자인 스페이스는 중첩등고선도 내의 목표 품질을 만족시킬 수 있는 설계 가능 영역을 의미한다. 중첩등고선도는 2차원의 형태로 표현되기 때문에 입력변수가 3개 이상일 경우, 디자인 스페이스를 나타내기 위해서는 하나 이상의 입력변수를 수준의 중심값으로 고정해야하며, 이로 인해 고정된 입력변수의 수준 변화에 따른 영향을 고려하지 못한다는 단점이 존재한다(Choi, 2016). 또한 디자인 스페이스는 오차의 분산이 클 경우, 설계 가능 영역 내에 존재하지만 규격의 상·하한선에 가깝게 위치한다면 실제로는 요구되는 반응변수의 규격을 만족시키지 못 할 확률이 높다(Jeong, 2017). 이러한 2차원의 디자인 스페이스의 한계점을 해결하기 위해 본 연구에서는 중첩등고선도 도출 시 고정되는 인자의 수준을 낮은 수준(-1)과 중간 수준(0), 그리고 높은 수준(+1)으로 고정하여 고정 인자의 각 수준별 설계공간을 도출한 후, 도출된 3개 수준의 설계공간을 모두 중첩시킴으로써 고정되는 인자의 영향까지 모두 고려할 수 있는 다차원의 디자인 스페이스(Multi-dimensional design space)를 도출하고자 한다. 또한 도출된 다차원 디자인 스페이스 내에서 목표 규격을 만족시킬 수 있는 보다 안전한 가용 영역(Safe operating space)과 그에 따른 허용 가능범위(Normal Acceptable Range, NAR)를 제시하고자 하며, 이는 아래 Figure 7과 같다. 다차원의 디자인 스페이스는 고정된 입력변수들의 수준 변화에 따른 영향을 고려할 수 있으므로 모든 입력변수의 변화에 대한 유연성을 가지며, 신뢰구간을 적용함으로써 다중의 입력변수 및 반응변수가 존재할 때 보다 신뢰성 높은 디자인 스페이스를 도출할 수 있다.
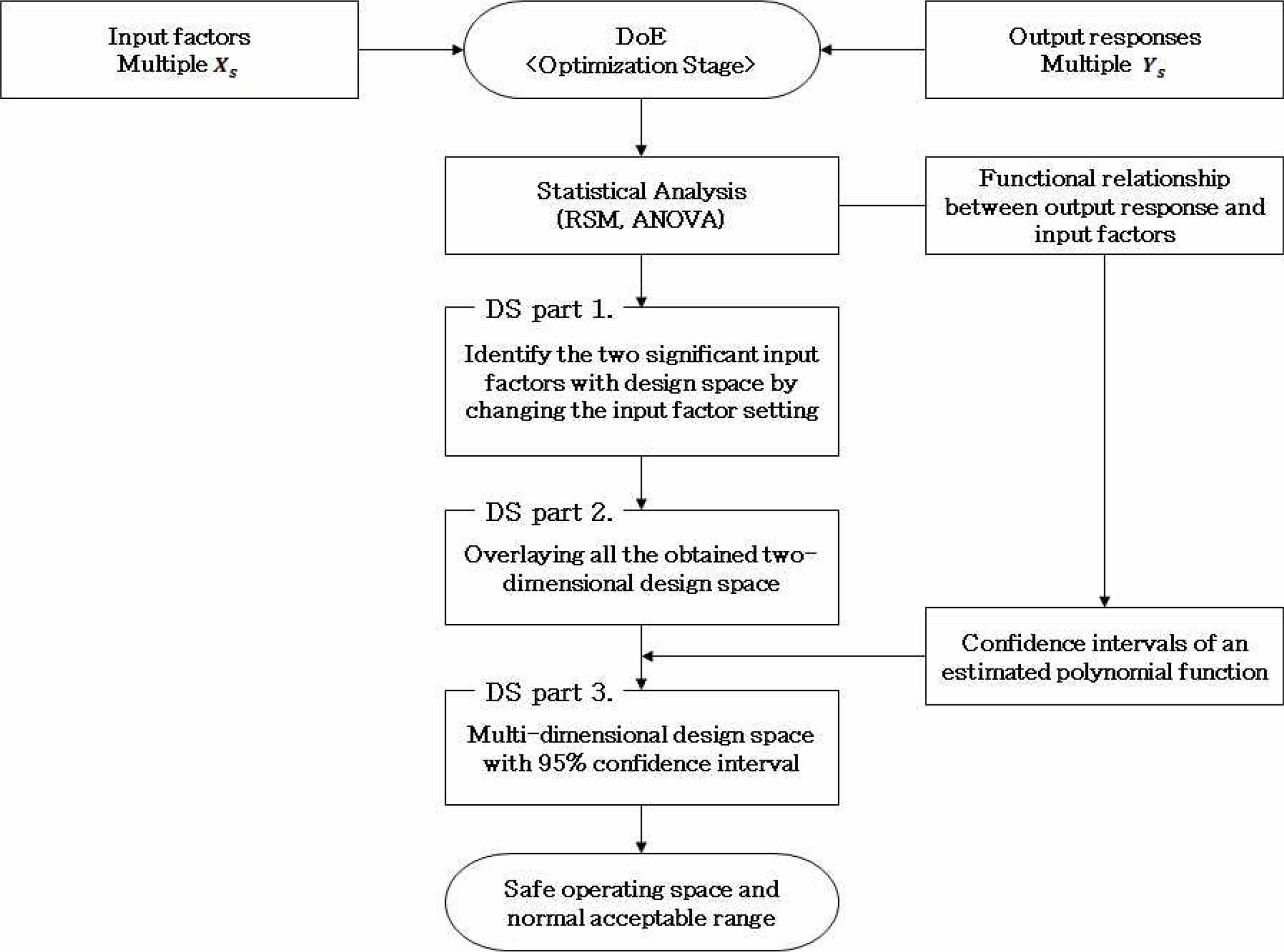
다차원의 디자인 스페이스와 신뢰구간을 바탕으로 안전가용영역 및 NAR이 도출되며, 이를 위한 절차는 아래 Figure 8과 같다. 우선, 선정된 주요입력변수와 주요품질특성간의 연관성 및 기능적 관계를 규명하기 위해 DoE의 여러 방법 중 CCD를 바탕으로 실험을 설계하여 최적화 단계의 실험을 수행하였다. 다음으로, 최적화 단계의 실험 결과를 바탕으로 분산분석(Analysis of variance, ANOVA) 등과 같은 통계적인 분석을 수행하였으며, 이를 통해 각 반응변수에 대한 입력변수들의 주효과 및 교호작용을 파악하고 각 반응변수에 대한 추정 회귀식을 도출하였다. 세 번째로, 디자인 스페이스 도출시 각 축에 고정할 2개의 주요입력변수를 선정하기 위해 추정된 회귀식을 바탕으로 각 입력변수를 낮은 수준(-1), 중간 수준(0), 높은 수준(+1)으로 변화시켜 각 수준별 중첩등고선도를 도출하였다. 도출된 중첩등고선도의 설계 가능 영역의 변화 양상 및 앞서 수행한 분산분석 결과를 바탕으로 반응변수에 가장 크게 영향을 미치는 2개의 입력변수를 선정하였다. 일반적으로 수준 변화에 따른 설계 가능 영역의 변화가 클수록, 분산분석의 p-value가 0.05이하이면서 0에 근사할수록 입력변수가 반응에 미치는 효과가 크다고 판단한다. 네 번째로, 선정된 주요 2개의 입력변수를 디자인 스페이스의 각 축에 고정하고, 나머지 입력변수를 특정 수준값으로 변화시켜 도출된 2차원의 중첩등고선도를 모두 중첩시켜 다차원의 디자인 스페이스를 도출하였다. 마지막으로, 다차원의 디자인 스페이스에 95% 신뢰구간(Confidence Interval, CI)을 적용하여 보다 강건한 다차원의 디자인 스페이스를 도출하였으며, 이를 통해 디자인 스페이스 내에서의 안전가용영역 및 NAR을 도출하였다.
다차원의 디자인 스페이스에 적용되는 신뢰구간은 앞서 수행된 최적화 단계의 실험 결과에 대한 분산분석을 통해 도출된 추정 회귀식을 바탕으로 산출되어지며, 추정 회귀식은 2.2절에서 제시한 식 (2)와 같다. 신뢰구간을 구하기 위해서는 특정 실험점(X0)에 대한 기댓값(E [ y ^ ( X 0 ) ] V a r [ y ^ ( X 0 ) ]
4. 연구 결과 및 분석
4.1 RSM 기반 단계적 실험 설계
본 연구에서는 실험설계를 위하여 RSM 기법 중 CCD를 사용하였고, CCD 실험 설계는 CCD가 가지고 있는 실험점(완전요인실험점, 축점, 중심점)의 특징을 살려 Figure 3과 3.2절의 Step2 및 Step3의 절차를 바탕으로 단계적 실험(특성화-최적화)을 수행하였다. 실험 설계에 앞서 저온의 SAW 프로세스에서의 주요품질특성 및 목표 품질을 정의하고 품질특성에 영향을 미치는 주요입력변수를 선별하였으며, 이를 바탕으로 실험의 범위를 설정하였다. 용접의 품질에 요구되는 기계적 성질 중 저온에서의 SAW 작업시 만족되어야 할 품질특성에는 인장강도, 연신율, 충격강도, 용접시간 등이 있으며, 이 중 제품의 품질 및 생산성과 직접적인 연관이 있는 특성은 충격강도와 용접시간이다. 본 연구의 목적은 저온에서의 용접의 품질을 향상과 동시에 생산성을 증대시키는 것에 있음으로 충격강도와 용접시간을 주요품질특성으로 선정하였으며, 이에 대한 목표 품질은 Table 1과 같다. 충격강도와 용접시간에 영향을 미치는 중간 단계의 특성(변수)으로는 입열량, 층간온도, 예열온도, 후열처리, 층간청결상태 등이 존재하며, 주요품질특성(충격강도, 용접시간)에 많은 영향을 미치는 중간 단계의 특성은 입열량이고, 이는 정성적인 스크리닝으로 도출되었다. 주요 중간 단계의 특성으로 선정된 입열량을 산출하기 위해서는 용접전류(A), 용접전압(V), 용접속도(cm/min)가 필요하며(ASME, 2017), 이 세 인자가 주요입력변수로 선정되었다. Table 2에 제시된 바와 같이, 실험의 범위는 용접 작업시 일반적으로 적용하는 범위를 포함하여 여러 번의 사전 시행착오 실험을 통해 용접이 가능하다고 판단되는 범위까지를 실험의 범위로 설정하였다(Kim, 2018).
선정된 주요입력변수(용접전압(X1), 용접전류(X2), 용접속도(X3)의 유의성을 평가하고 실험 범위의 타당성을 평가하기 위해 특성화 단계 실험을 수행하였다. 특성화 단계는 3인자 2수준의 완전요인실험에 중심점을 추가하여 9개의 실험점으로 설계되었으며, 3번의 반복 실험을 수행하여 총 27번의 실험을 수행하였다. 실험 결과에 대한 통계적인 분석을 수행하기 위해 충격강도(Y1)의 경우 3번의 반복 실험의 평균값을 사용하였으며, 용접시간(Y2)의 경우 전류, 전압, 속도의 조건에 의해 정해지는 것으로 같은 조건하에서는 항상 일정한 값이 도출되어 평균값이 아닌 개별값을 사용하였다. 특성화 단계 실험 결과에 대한 분산분석을 수행한 결과, 충격강도와 용접시간에 대한 모형의 p-value는 각각 0.029와 0.005로 유의하였고 R-square는 모두 70% 이상으로 추정된 모형이 데이터를 잘 대변하고 있는 것으로 나타났다. 그리고 두 품질특성(충격강도-망대, 용접시간-망소)이 반대의 특성을 가지고 있어, 곡률효과는 유의하게 나타나지 않았지만, 입력변수의 수준이 변함에 따라 반응변수에 유의한 영향을 미친다고 보이며, 이에 선정된 입력변수가 유의하고 실험의 범위가 적절히 설정되었다고 판단된다.
특성화 단계를 통해 입력변수의 유의성 및 실험 범위의 타당성에 대해 입증하였으며, 각 반응변수에 대한 모형의 p-value가 대부분 0에 가까웠으므로 최적화 단계의 실험 설계 시 범위의 변동없이 축점과 중심점만을 추가함으로써 더욱 정밀한 실험 및 분석이 가능한 CCF 방법을 사용하였다. 최적화 단계는 앞서 수행한 특성화 단계의 실험점(완전요인실험점과 일부 중심점)과 추가적으로 수행된 6개의 축점 및 5개의 중심점으로 총 20개의 실험점으로 구성되며, 3번의 반복을 수행하여 총 60번의 실험을 수행하였다. 이에 대한 실험 결과는 아래 Table 3과 같다.
4.2 최적화 단계 실험 결과 분석
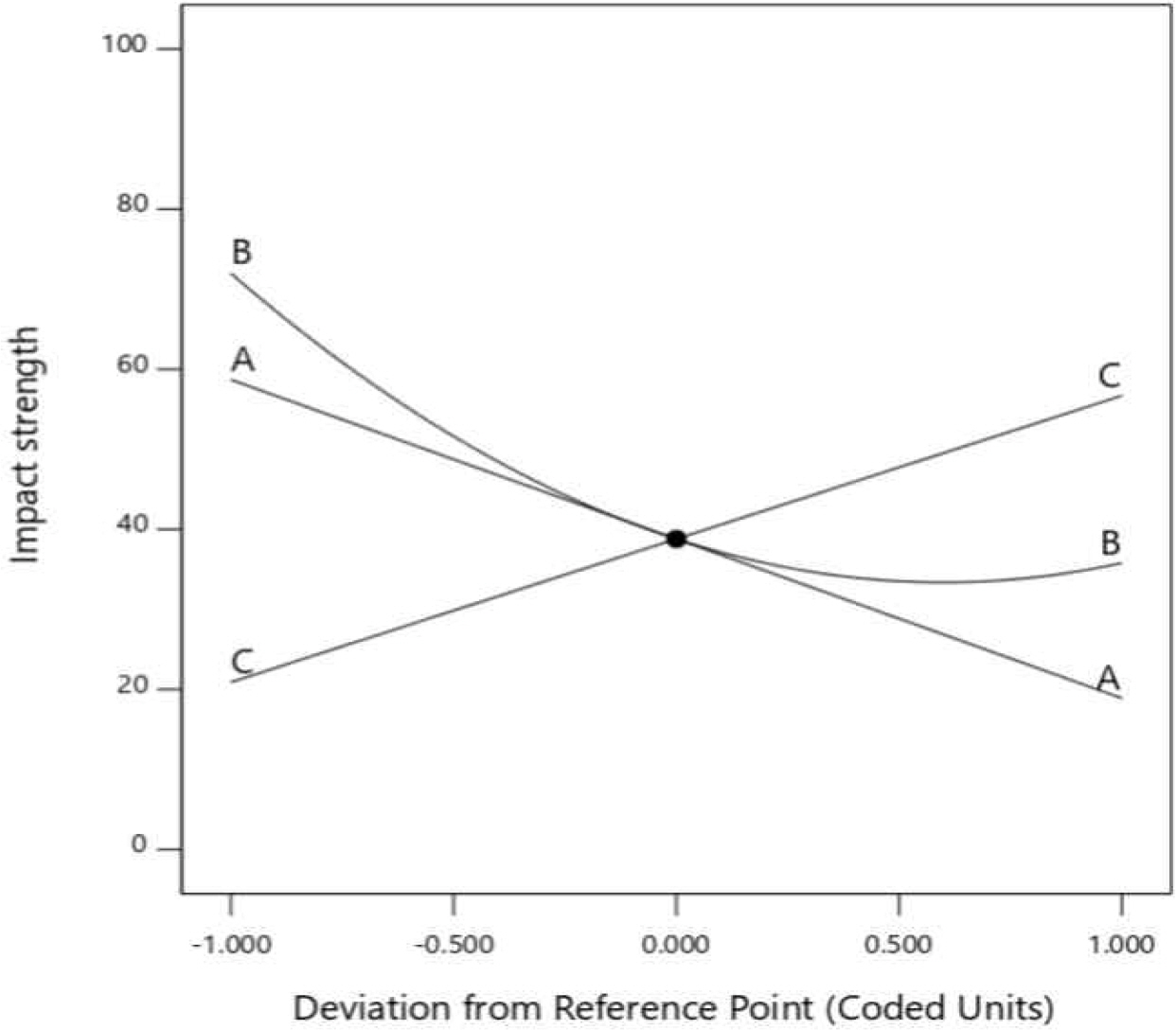
최적화 단계 실험의 결과를 바탕으로 각 반응변수에 대한 분산분석 및 주효과도를 통한 통계적 분석을 수행하였다. 먼저, 충격강도(Y1)에 대한 분산분석 결과는 아래 Table 4와 같으며, 모형의 p-value는 0.000으로 유의하였고 R-square는 71.93%로 나타났다. 충격강도에 대한 주효과와 교호작용 항에 대한 유의성 검정 결과, 용접전류(X1), 용접전압(X2), 용접속도(X3) 모두 충격강도에 영향을 미친다고 판단되며, 각 인자간의 교호작용에 의한 효과는 나타나지 않았다. 각 입력변수의 수준이 변함에 따라 반응변수에 미치는 영향을 시각적으로 파악하기 위해 Figure 9와 같은 주효과도를 확인하였으며, 그 결과 용접의 전류와 전압이 낮을수록, 속도가 빨라질수록 충격강도가 증가하는 효과를 보였다. RSM분석 결과 충격강도에 대한 추정 반응함수는 다음과 같다.
다음으로, 용접시간(Y2)에 대한 분산분석 결과는 아래 Table 5와 같으며, 모형의 p-value는 0.001로 유의하였고 R-square는 73.33%로 나타났다. 주효과와 교호작용 항에 대한 분석 결과, 용접전류가 증가할수록 용접시간이 줄어듦을 알 수 있었으며, 용접시간의 제곱항(A*A)항의 p-value가 0.043으로 유의함에 따라 곡률효과가 있을것이라 판단된다. RSM분석 결과 용접시간에 대한 추정 반응함수는 다음과 같다.
최적화 단계 분석 시 보다 강건한 최적해를 도출하기 위해 충격강도에 대한 반복 실험시 발생하는 표준편차(Y3)를 하나의 반응변수로 고려하여 통계적인 분석을 수행하였다. 그 결과, 분산분석에 의해 도출된 모형의 p-value가 0.081로 유의하지 않게 나타났으나, 신뢰수준 90%내에서는 만족하는 결과이므로 추후 더욱 신뢰성 높은 결과값을 도출하기 위해 충격강도에 대한 표준편차를 고려하여 디자인 스페이스를 도출하였다.
4.3 안전가용영역 및 최적조합 도출
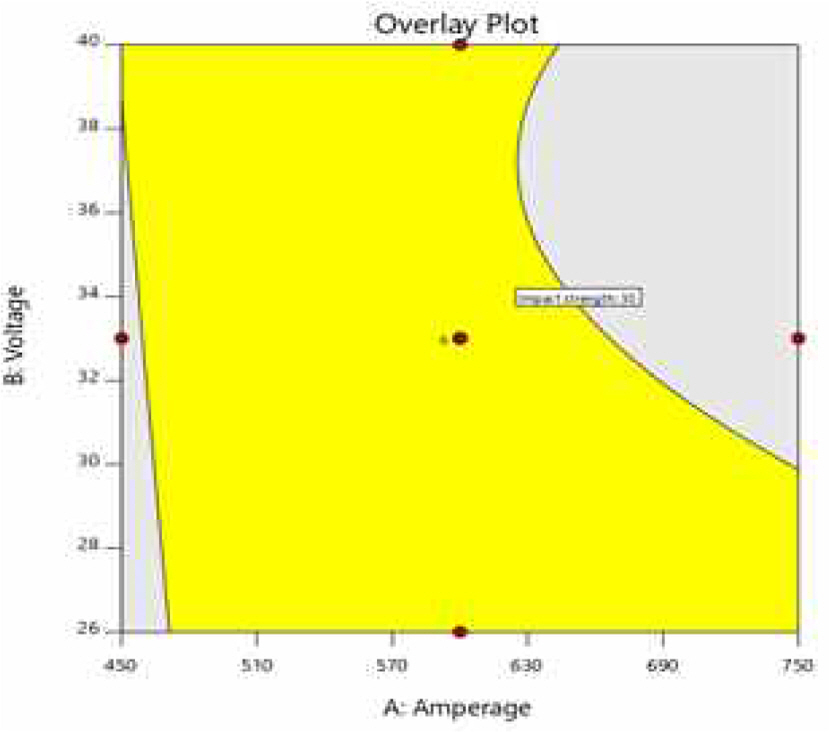
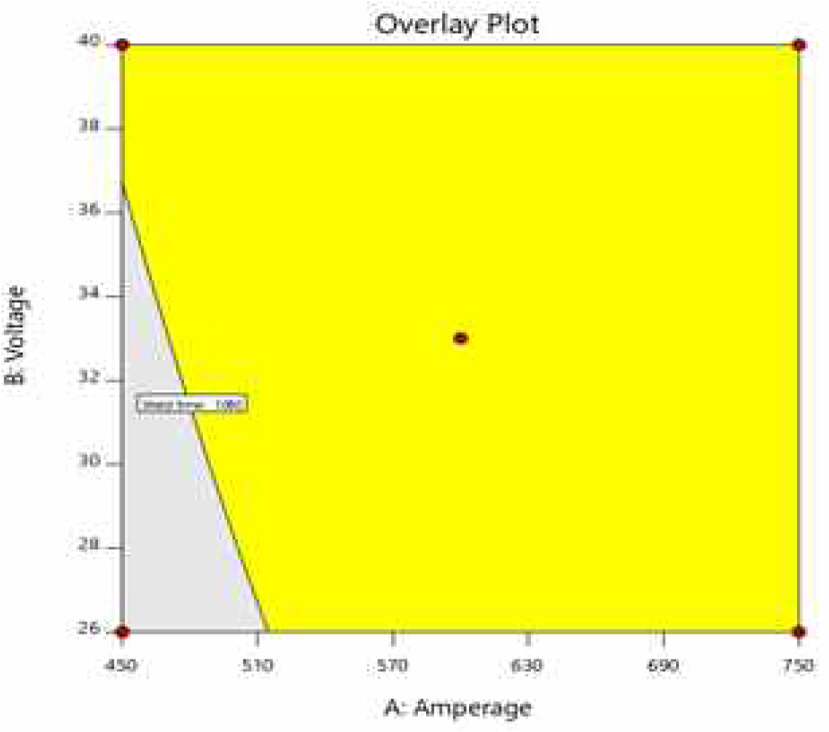
최적화 단계에서 도출된 각 반응변수의 추정 회귀식을 바탕으로 디자인 스페이스롤 도출하여 디자인 스페이스 내에서 목표 품질을 항상 만족 시킬 수 있는 안전가용영역과 가용영역 내에서 목표 품질을 가장 만족시킬 수 있는 입력변수의 최적조합을 도출하였다. 우선, 디자인 스페이스를 도출하기 위해서는 디자인 스페이스의 각 축에 고정할 2개의 주요입력변수를 선별해야하며, 이를 위해 반응변수의 목표 품질을 상·하한으로 설정하여 각 입력변수의 수준별 중첩등고선도를 도출하였다. 세 개의 입력변수 중 두 개의 입력변수를 각 축에 고정하고 고정되지 않은 나머지 인자를 낮은 수준(-1), 중간 수준(0), 높은 수준(+1)의 세 가지 수준으로 변화시켜 총 9개의 중첩등고선도를 도출하였다.
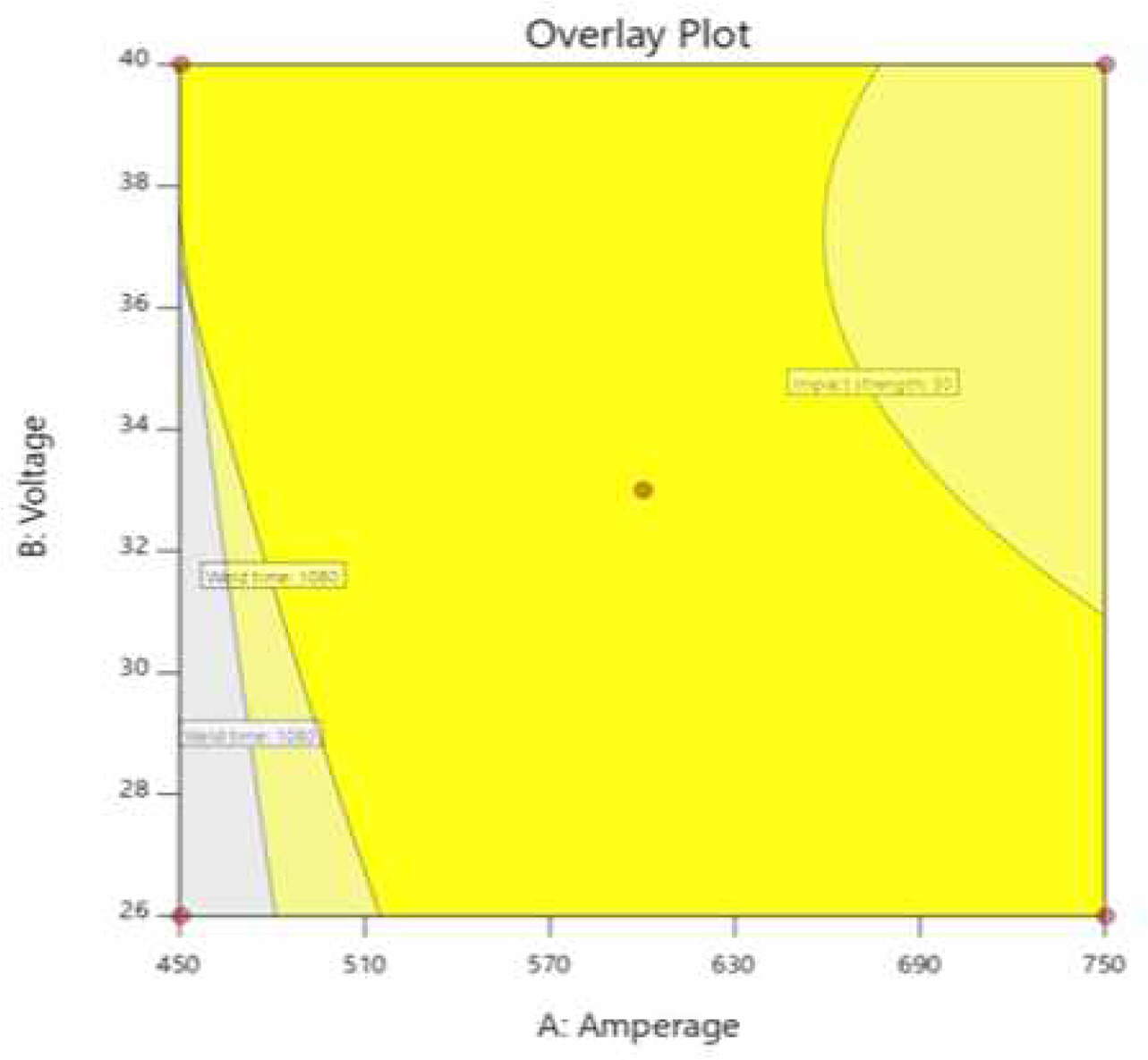
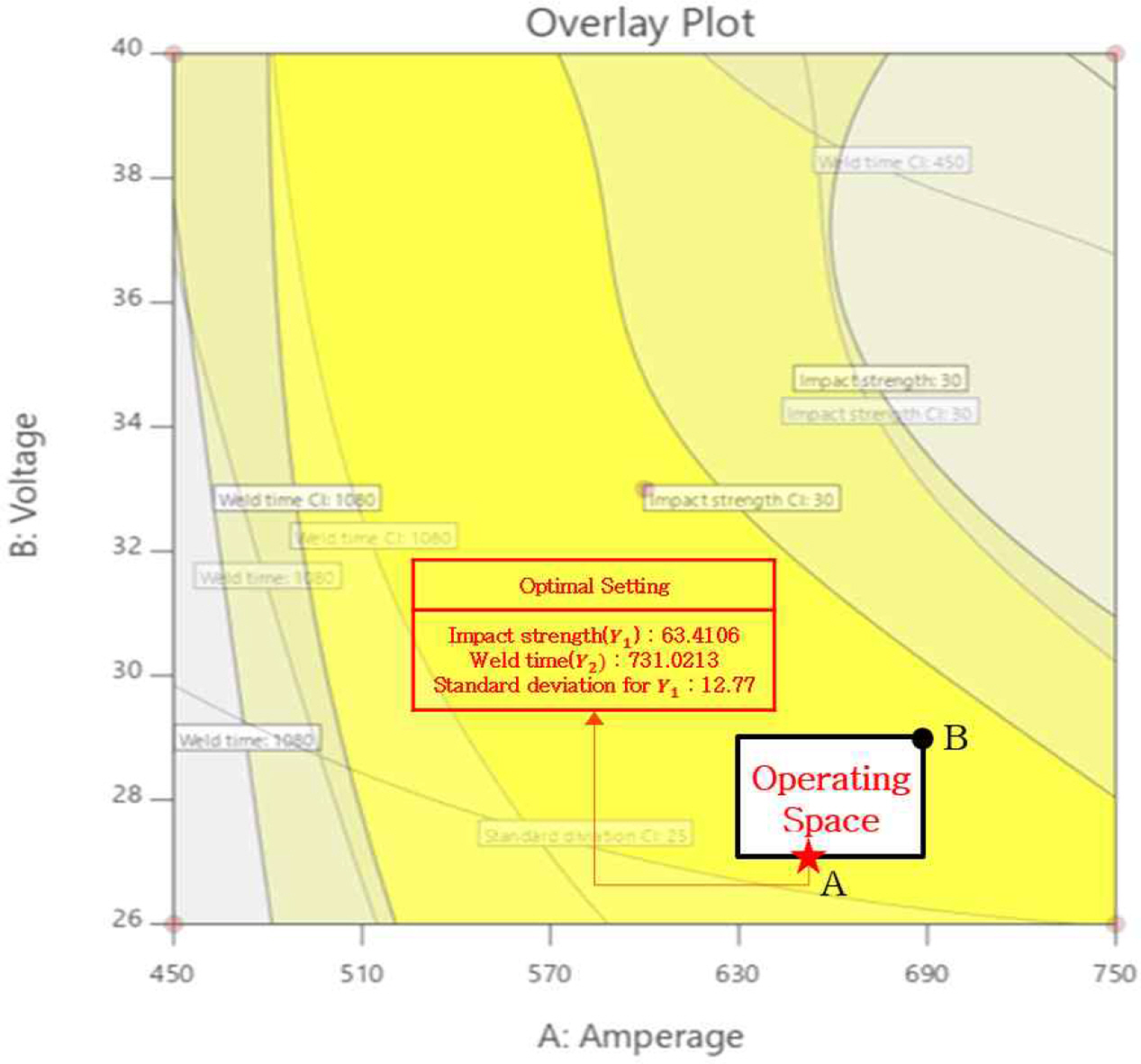
각 입력변수의 수준변화에 따른 디자인 스페이스 영역 변화정도를 살펴본 결과, 용접전류, 용접전압, 용접속도 순으로 영역의 변화가 많이 나타남을 확인하였다. 따라서 앞서 수행한 분산분석 결과와 종합해 볼 때, 용접전류와 용접전압이 반응변수에 더 많은 영향을 미친다고 판단되어, 9개의 중첩등고선도 중 용접전류와 용접전압을 디자인 스페이스 상의 각 축에 고정시키고 용접속도를 수준으로 고정시켜 도출된 아래의 Figure 11~Figure 13과 같은 3개의 중첩등고선도를 선정하였다. 아래의 세 중첩등고선도를 모두 중첩하여 모든 반응변수와 입력변수가 고려된 다차원의 디자인 스페이스가 도출되게 되는데, 아래 세 개의 중첩등고선도를 살펴보면 용접속도의 수준이 낮아질수록 디자인 스페이스의 영역이 줄어듦을 알 수 있다. 따라서 더욱 안전한 디자인 스페이스를 도출하고자 용접속도의 수준을 11과 12.5로 조정하여 다시 중첩등고선도를 도출하였으며, 도출된 두 개의 중첩등고선도를 중첩시킴으로써 아래 Figure 14와 같은 다차원의 디자인 스페이스를 도출하였다. 또한 더욱 강건한 안전가용영역을 도출하기 위해 다차원의 디자인 스페이스에 95% 신뢰구간을 적용하였으며, 신뢰구간이 적용된 다차원의 디자인 스페이스는 아래 Figure 15에 제시하였다.
디자인 스페이스 내에서 반응변수의 목표품질을 가장 만족시킬 수 있는 안전가용영역을 도출하기 위해 여러 가지 경우의 안전가용영역을 도출하여 각 반응변수의 추정 회귀식을 통해 최적해를 예측해보았으며, 그 결과 목표 규격을 가장 만족시키는 아래 Figure 15와 같은 안전가용영역을 최종적으로 도출하였다. 안전가용영역에 따른 NAR은 아래 Table 6와 같으며, 이를 바탕으로 가용영역 내에서의 최적 조합을 도출하기 위해 최적화 분석을 수행하였다. 최적화 분석 시 반응변수의 목표 품질은 위에서 제시한 Table 1과 같이 설정하였으며, NAR 내에서 가장 만족하는 최적해를 도출하기 위해 전류를 630~690, 전압을 27~29, 속도를 11~12.5로 고정하여 해당 영역 내에서 최적조합을 찾을 수 있도록 설정하였다. 그 결과, 도출된 최적 조건(Optimal setting)은 Table 7과 같으며, 전류(X1), 전압(X2), 속도(X3)가 각각 649, 27, 11일 때 충격강도(Y1)는 63.4, 용접시간(Y2)은 731.0, 충격강도의 표준편차(Y3)는 12.8의 최적값을 가진다.
4.4 최적화 결과의 검증(Validation)
위의 Figure 15에서 제시한 최적 조합(A점)과 안전가용영역 내에서 생산성이 가장 좋을 것이라 예측되는 B점에 대해 재현성 실험을 진행하였다. 그 결과, Table 8에 제시한 바와 같이 두 개의 실험점 모두 충격강도와 충격강도의 표준편차는 예측값과 실제값이 약간의 차이를 보였으며, 용접시간은 비슷하게 나타났다. 예측값과 실제값의 차이는 실험 환경 및 반복에 의한 오차로 보이며, 대체적으로 예측값과 실제값이 유사하게 나타나 최적화 결과가 충분한 신뢰성 및 유의성을 지닌다고 판단된다. 또한 두 실험점의 검증 실험 결과를 비교해 볼 때, 실점점 A의 충격강도가 더 높고, 용접시간이 더 짧은 것으로 타나나 실험점 A의 조건으로 용접을 수행할 경우 실험점 B의 조건으로 수행하는 것보다 품질 및 생산성이 더 좋게 나타날 것이라 판단된다.
5. 결 론
본 연구에서는 저온용 강판의 자동용접(SAW)작업을 연구대상으로 하여 단계적 실험계획법(DoE)을 활용하여 용접품질에 요구되는 기계적 성질 중 저온에서의 충격강도 및 용접시간에 영향을 미치는 인자를 파악하고 선별하여 용접작업의 안전가용영역 및 최적의 용접작업 조건을 도출하였다. 그리고 도출된 최적 조합에 대한 재현성 실험을 실행하여 그 결과가 예측된 품질수준을 만족하는지 확인하였다. 충격강도와 용접시간에 유의한 영향을 미치는 인자를 선별한 결과, 용접전류, 용접전압, 용접속도가 선정되었다. 이를 토대로 단계적 DoE를 적용하여 실험을 수행하였으며, 그에 따른 결과를 분석하였다. 충격강도에는 선정된 세 가지 인자 모두 유의한 영향을 미치는 것으로 나타났으며, 전류와 전압의 수준이 낮을수록, 속도의 수준이 높아질수록 충격강도가 높아지는 효과를 보였다. 반면, 용접시간에는 전류만이 유의한 영향을 미치는 것으로 나타났으며, 충격강도와 반대로 속도의 수준이 높아질수록 용접시간이 줄어드는 효과를 보였다. 이러한 분석 내용을 토대로 충격강도와 용접시간의 목표 품질을 동시에 만족시킬 수 있는 용접 작업 영역을 탐색하기 위해 신뢰구간을 적용한 다차원의 디자인 스페이스를 도출하였으며, 이를 바탕으로 NAR 및 최적조건을 제안하였다.
본 연구 결과를 통해 작업의 조건이 적절하게 관리됨에 따라 품질 및 생산성 향상에 크게 기여할 것이라 판단되고, WPS 작성시 실험계획법을 사용함으로써 최소의 실험으로 많은 정보를 확보하고 이로 인해 비용절감의 효과가 있을 것으로 기대된다. 향후 시장에서 사용 용도가 많은 재질의 모재와 다양한 Welding process, 즉 SMAW, FCAW, GTAW 등으로 연구범위를 확대해 기업에서 최적의 조건으로 용접작업을 수행할 수 있도록 지속적인 연구 활동이 요구되며, 경도 등 다른 기계적 성질 값과 상관관계에 따른 최적화 조건 등의 연구 활동이 이루어져야 할 것이다. 또한, 저온의 충격강도 실험이 노이즈에 영향을 받을 수 있는 가능성이 있다고 판단되어, 향후 노이즈를 고려한 실험 설계 방법을 적용할 수 있는 방안의 연구가 필요하다고 판단된다.