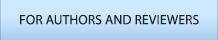배관의 부식은 장기사용 배관의 위험요인이다. 배관 표면에 발생한 부식결함을 식별하고 시간에 따른 부식성장을 모니터링하는 것은 장기사용 배관의 건전성 관리에 중요한 역할을 차지한다(Kim et al. 2017). 사용 중인 배관의 상태를 점검하기 위해 라인내 검사(In-line Inspection)를 정기적으로 실시한다. 이 때 배관 내부로 투입되는 측정 장비를 피그(Pig)라고 부른다. 라인내 검사는 크게 Magnetic Flux Leakage(MFL) 방식과 Ultrasonic 방식으로 구분되는데 다음 그림은 MFL 검사로 얻은 3차원 결함정보를 배관두께에 대한 2차원 변수로 변환하는 과정을 개략적으로 나타낸 것이다. 이렇게 얻어진 결과를 토대로 부식결함의 발생 위치, 형상, 크기 등을 기록한 파일을 피깅(Pigging) 데이터셋이라고 부른다. 일반적으로 MFL 방식에 따른 피깅 데이터는 10% 내외의 측정 및 계산 오차를 포함하는 것으로 알려져 있다(Cosham et al. 2007).

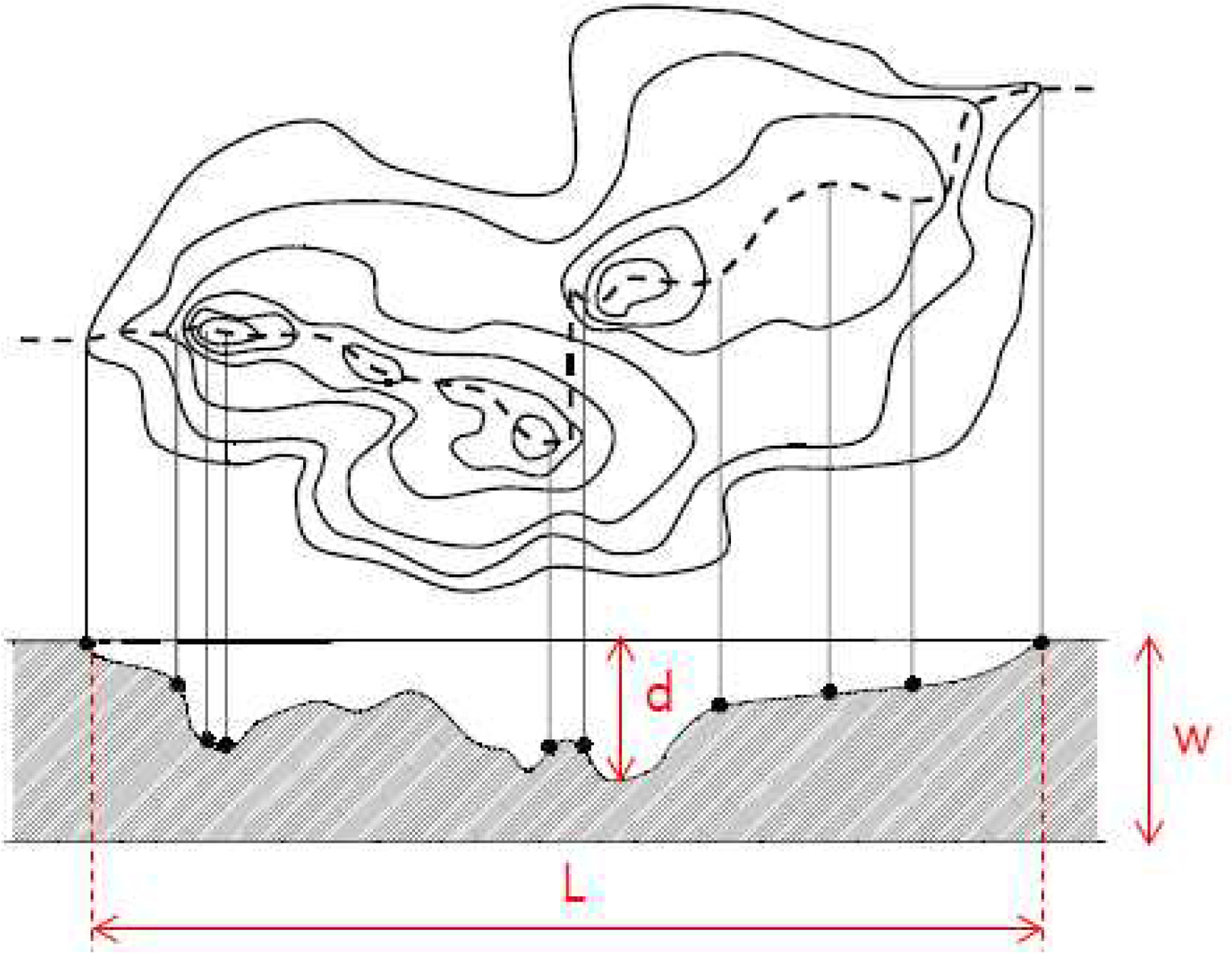
그림 1에 나타낸 바와 같이, 부식결함의 크기는 깊이 d와 길이 L로 기록된다. w는 배관의 두께를 의미한다. 캐나다 표준협회가 제정한 석유 및 가스 배관에 관한 표준규격 CSA Z662-2007에 따르면, 부식과 관련된 배관 고장은 Small Leak, Large Leak, Rupture 등 3가지로 구분된다. 이는 아래 그림 2에서 보는 바와 같이 부식결함의 깊이와 길이를 기준으로 한 것이다.

Small Leak는 길이는 매우 짧지만 깊이가 큰 핀홀 형태의 부식결함으로 인해 가스가 누설되는 것을 말한다. Large Leak는 국부적인 부식결함으로 인해 배관의 잔류강도가 약화되면서 가스가 누설되는 것이고, Rupture는 배관 전역에서 부식이 광범위하게 진행되어 심각한 두께 및 강도 손실과 함께 파단이 일어나는 것을 뜻한다. 그림 안에 g₁, g₂, g₃라 표기한 것은 이들 3가지 고장에 대응하는 한계상태함수이다. 그림을 보면, g₂가 대부분의 영역을 포괄하고 있음을 알 수 있는 데 바로 배관의 파열(Burst)이 여기에 해당된다.

파열압력이란 파열이 발생하는 압력을 말하는 데 배관 내부의 압력이 이를 초과할 경우 배관의 파열이 발생한다는 의미이다. 파열압력은 배관의 강도, 직경, 두께 등의 함수이고 특히 부식 깊이와 길이에 의해 큰 영향을 받는다. 이에 따른 파열압력 계산식으로 널리 이용되는 코드는 PCORRC, ASME Modified B31G, DNV-99 등이다. 각각의 특징이나 차이점에 대해서는 Caleyo et al.(2002)의 연구를 참고하기 바란다. 본 논문은 선행연구인 Kim et al. (2019)에서와 같이 국내에서 널리 채택되고 있는 PCORRC를 사용한다. 이때 파열압력 P_b의 계산식은 다음과 같다.

단 U, D, w는 배관의 인장강도, 직경, 두께를 각각 나타낸다. 그리고 d와 L은 부식결함의 깊이와 길이를 의미한다. 부식 깊이와 길이는 시간에 따라 커지게 되므로 파열압력은 시간에 따라 감소하는 형태가 된다. 특히 d가 w로 접근하면 파열압력은 0으로 수렴하게 됨을 알 수 있다. 반면 d가 충분히 작을 때에는 L은 파열압력에 그리 큰 영향을 미치지 않는다.

배관의 신뢰도 평가를 위해서는 우선 배관의 고장을 정의하는 한계상태함수를 결정해야 한다. 본 논문에서는 CSA Z662-2007에서 제시한 g₂를 채택하고자 한다. 이는 파열압력 P_b과 운영압력 P_op의 차이로서 g₂ = P_b - P_op와 같이 쓸 수 있다. 전술한 바와 같이, 운영압력이 파열압력을 초과하면 배관의 고장이 발생한다는 의미이다. 파열압력과 운영압력을 확률변수라고 하면 배관의 신뢰도 R은 파열압력이 운영압력보다 클 확률 또는 한계상태함수가 0보다 클 확률로 정의되어지며 아래 식으로 나타낼 수 있다.

따라서 신뢰도를 구하기 위해서는 P_b와 P_op의 결합 확률분포가 필요하다. 보통은 P_b와 P_op는 서로 독립으로 간주될 수 있으므로 개별 확률분포가 주어지면 강도-부하 모형을 이용하여 어렵지 않게 신뢰도를 계산할 수 있다. 예를 들어 확률변수 P_b와 P_op가 서로 독립이며 정규분포를 따른다고 가정하자. 그리고 P_b의 평균과 표준편차를 각각 μ_b와 σ_b로 놓고 P_op의 평균과 표준편차를 각각 σ_op와 σ_op라 놓으면 식 (2)의 신뢰도는 다음과 같이 나타낼 수 있다.

단 Φ(·)는 표준정규분포의 분포함수를 나타내고 특히 β = (μb - μop)/σb2 +σop2 는 신뢰도 지수(Reliability Index)라 칭한다. 신뢰도 지수 β가 클수록 신뢰도는 1에 가까워진다.

물론 이러한 신뢰도 평가는 파열압력과 운영압력이 서로 독립인 정규분포를 따를 때 가능하다. 하지만 정규분포를 따른다는 보장이 없고 심지어 파열압력에 대한 확률분포는 알 수 없는 경우가 많다. 사실, 운영압력에 대한 확률분포는 배관운영회사에서 측정을 통해 용이하게 확보할 수 있지만 현재 사용하고 있는 배관의 파열압력은 측정 자체가 불가능하거나 식 (1)로도 볼 수 있듯이 많은 변수의 영향과 불확실성 하에 있기 때문에 확률분포를 수리적으로 유도하는 것은 매우 복잡하다. 배관 신뢰도를 구하고자 할 때 등장하는 이러한 문제점을 해결하기 위해 근사해법 또는 Monte Carlo Simulation(MCS)이 적용되어 왔다.

근사해법으로는 First Order Second Moment(FOSM), First Order Reliability Method(FORM), Second Order Reliability Method(SORM) 등을 들 수 있다. 이들은 적용하기 간편하지만 정규분포를 가정한다는 점과 식 (1)의 파라미터 설정에 민감하다는 점이 한계이다. 특히 이들은 분산을 추정할 뿐이지 분포 자체를 추정하는 방법은 아니라는 점도 상기해야 한다. MCS를 이용하면 식 (1)을 이용하여 많은 표본을 발생시켜서 경험적 분포를 구하거나 기존 확률분포에 적합시키는 것이 가능하다. 예를 들어, Caleyo et al. (2009)는 MCS를 이용하여 부식 깊이와 성장속도에 대한 확률분포를 추정하였다. Hasan et al. (2012)는 MCS를 이용하여 파열압력의 분산을 추정하고 신뢰도 지수를 계산하였다. Qian et al. (2013)은 한계상태함수를 평가하고 고장확률을 계산하는 데 MCS를 이용하였다. 이처럼 MCS는 배관 신뢰도 문제를 다룰 때 다각적으로 적용되고 있지만 파열압력의 확률분포를 직접적으로 다룬 연구는 상대적으로 미흡한 실정이다.

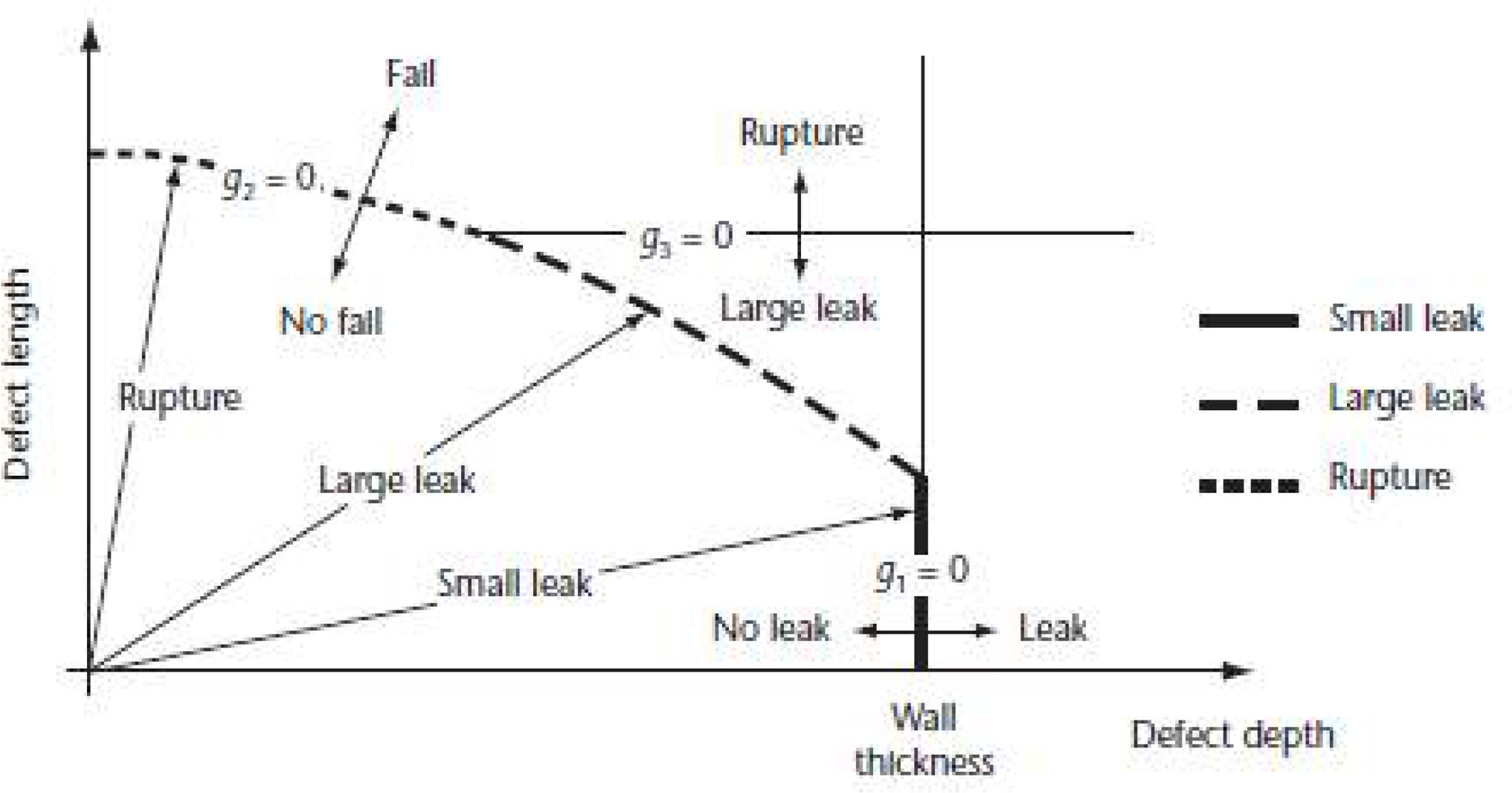
본 논문은 배관의 신뢰도 평가에 요구되는 파열압력의 분포추정을 위해 MCS를 이용하는 방안을 제안한다. 특히 부식결함의 깊이와 길이 수준에 따라 다양한 확률분포가 나타날 수 있기 때문에 반응표면 실험계획법을 이용하여 분포 파라미터 모델을 구축하고 활용하는 과정을 API 5L X65 배관을 대상으로 예시한다. 아래 그림 3은 본 연구의 내용을 토대로 API 5L X65 배관의 신뢰도를 평가하는 절차를 보여주고 있다.

API 5L X65 등급 배관은 국내 천연가스 공급을 담당하고 있는 주요 배관 중 하나이며 직경은 508mm 또는 762mm, 두께는 10.3mm에서 17.5mm까지 다양한 제품군으로 이루어져 있다. 본 연구는 17.5mm 배관을 대상으로 파열압력 분포의 추정 문제를 다룬다. 그림 3에서 나타낸 바와 같이, 파열압력을 계산하기 위해서는 인장강도, 직경, 두께, 부식 깊이, 부식 길이 등을 입력해야 한다. X65 배관의 경우 각 변수들의 공칭 값은 표 1과 같이 주어진다.

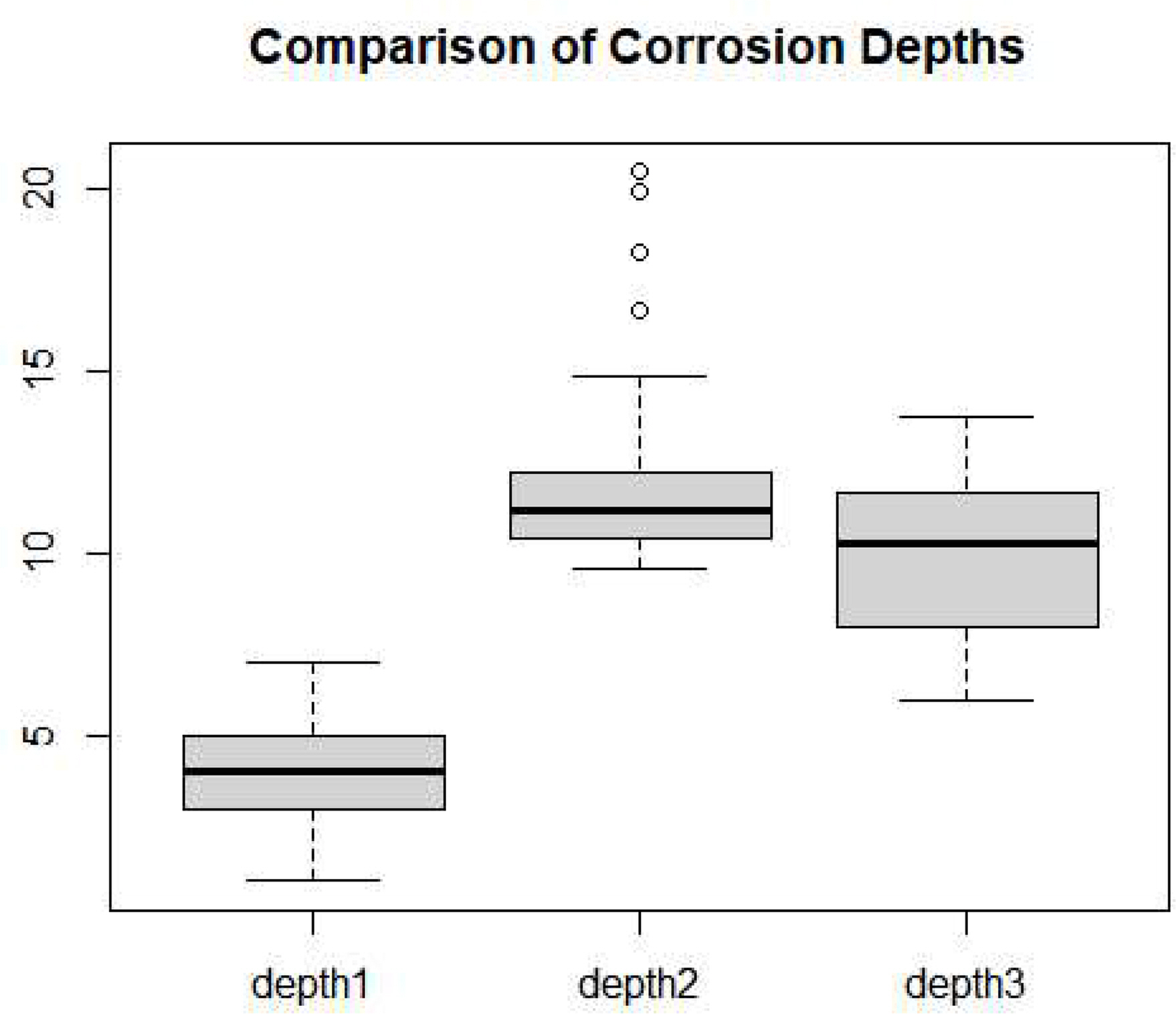
각 변수의 확률분포는 CSA Z662-2007이 권고한 내용을 따르기로 한다. 표 1에서 볼 수 있듯이, 기초 변수의 확률분포는 서로 독립인 정규분포를 가정한다. 다만 부식결함의 크기에 대해서는 정규분포 외에도 와이블분포나 대수정규분포의 적용이 가능하다. MCS 수행을 위해서는 확률분포의 평균과 표준편차가 필요하다. 평균은 표 1의 공칭 값을 그대로 사용하지만 표준편차는 관련 규격이나 사내 운영데이터를 이용해서 결정해야 한다. 배관공학 분야에서는 표준편차 대신 변동계수(COV)를 많이 이용하는 데, CSA Z662-2007이 제시한 변동계수 설정기준에 따르면 인장강도는 4%, 배관직경은 0.06%, 배관두께는 1% 정도가 적절할 것으로 판단된다. 배관 시스템의 신뢰도 기법에 관한 국제규격인 ISO 16708-2006(E)에서도 인장강도 1.5-6.0%, 배관직경 0.1% 미만, 배관두께 0.5%-2.0%로 변동계수를 다룰 것을 권고하고 있으므로 대체로 비슷한 수준이다. 다만 부식결함의 경우는 매설 지역과 기간에 따라 변동이 크기 때문에 현장에서 수집된 데이터에 근거하여 변동계수를 설정하는 것이 타당할 것이다. 예를 들어, Qian et al.(2013)은 부식결함의 깊이와 길이에 대해 변동계수를 각각 10%로 채택하였다. 이보다는 큰 값으로 Zhang et al.(2019)의 연구에서는 깊이를 약 40%, 길이를 약 20%로 변동계수를 적용하였다. 본 연구에서는 10km 이상 구간에서 수집된 6가지 피깅 데이터셋을 검토한 결과, 깊이와 깊이의 COV가 각각 15-48%, 14-51% 수준으로 얻어졌다. 이를 근거로 할 때 부식결함의 COV는 대략 10-50% 범위에서 선택하되 해당 구간의 매설기간이나 환경적 특성을 고려하는 것이 바람직할 것으로 사료된다. 참고로, 그림 4는 어떤 3개의 구간에서 검출된 부식결함의 깊이를 상자 그림으로 간단하게 나타낸 것이다. 대상 구간에 따라서 변동에 차이가 나타날 수 있음을 예시하고 있다.

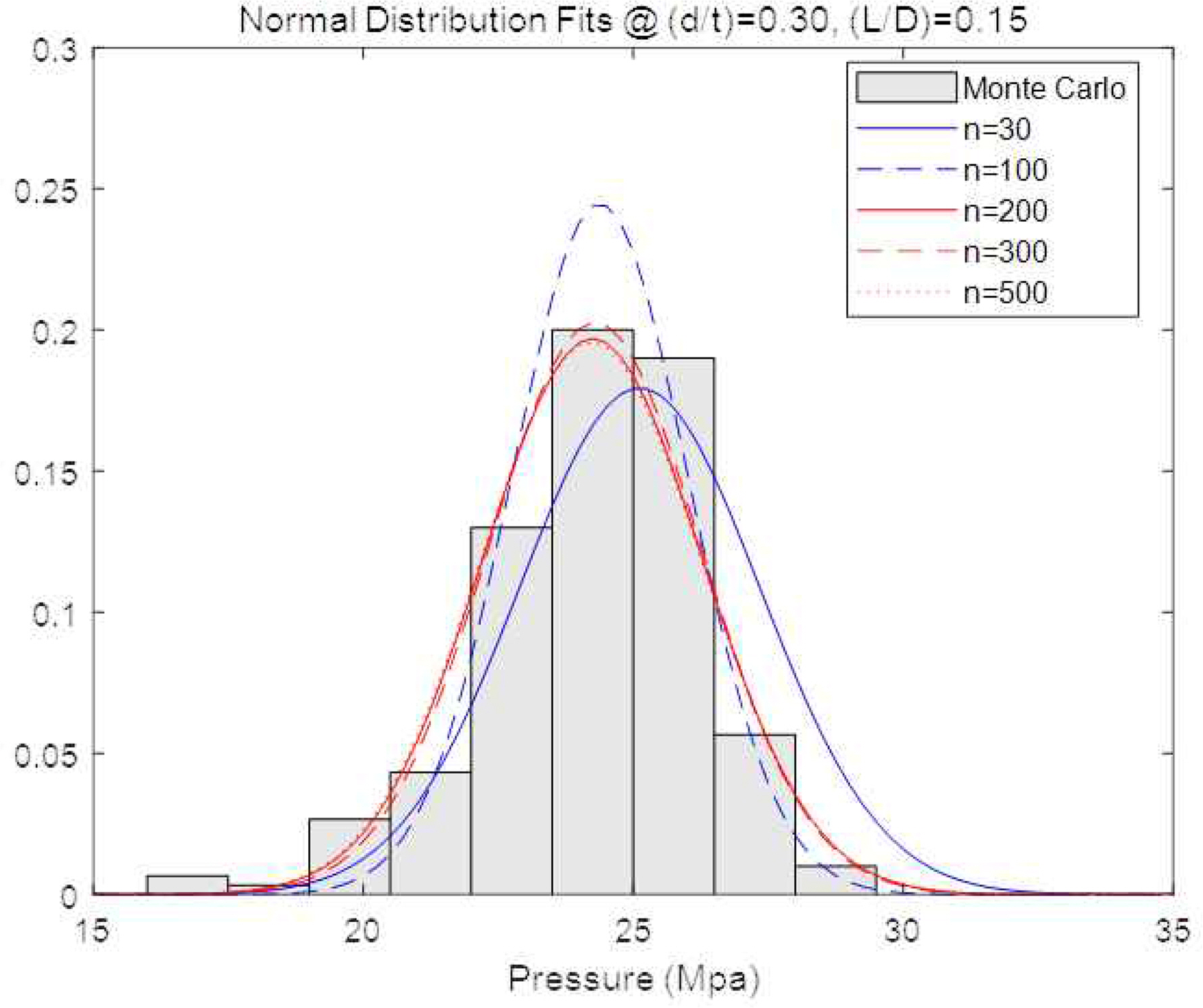
그림 5는 어떤 부식결함에 대해서 깊이와 길이의 COV를 각각 50%로 하였을 때 MCS를 통해 얻은 파열압력의 분포를 보여준다. 런 수가 늘어남에 따라 분포의 모습이 안정화되고 있다. 대체로 정규분포에 가까운 모습이고 런 수가 200 정도이면 큰 변화를 나타내지 않으며 분포를 추정하는 데 충분할 것으로 판단된다. 이러한 관측을 근거로 본 연구에서는 MCS 런 수로 200회로 설정한다.

그림 5의 부식결함은 Depth to Thickness Ratio와 Length to Diameter Ratio를 각각 30%, 15%로 적용한 것이다. 이후로는 이를 (d/t)=0.3, (L/D)=0.15로 표기하기로 한다. 여기서 이 조건을 선택한 이유는 그림 2에 나타낸 고장 발생 주요 영역의 중앙 지점에 해당되기 때문이다. 전술한 바와 같이 (d/t)와 (L/D)는 매설 지역과 기간에 따라 다양하게 변동하기 때문에 여러 조합에서 파열압력의 변화를 관찰할 필요가 있다. 본 연구는 반응표면 실험계획법을 이용하여 (d/t)와 (L/D)의 대표 조합을 구하고 파열압력 분포의 파라미터를 모델링하고자 한다.

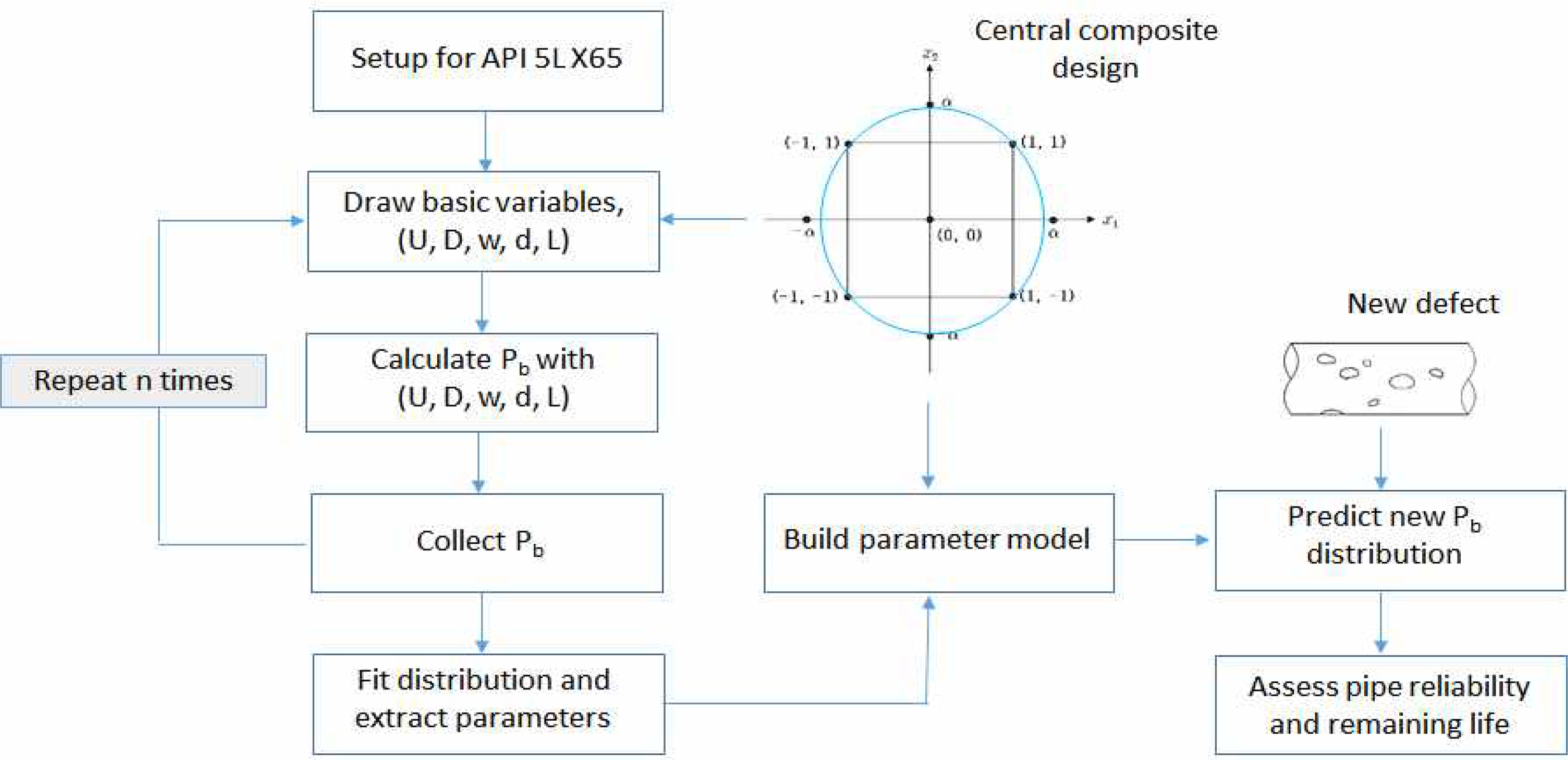
반응표면 실험계획법은 공정이나 제품의 최적 설계조합을 찾고자 품질공학 분야에서 널리 이용되는 기법으로, Kim et al. (2016)의 리뷰논문을 통해 품질 분야의 활용 현황을 찾아볼 수 있다. 반응표면 실험계획법은 Central Composite Design과 Box-Behnken Design으로 나뉘는 데 본 실험에서는 설계인자가 X₁ = (d/t)와 X₂ = (L/D), 2개이므로 전자를 채택한다. 기존의 피깅 데이터셋을 검토했을 때 X₁과 X₂의 실험영역은 각각 0.1에서 0.5, 0.05에서 0.25로 정하면 적절할 것으로 판단된다. 이 경우, 중심점은 (0.30, 0.15)가 되고 축점은 (0.5828, 0), (0.0172, 0), (0, 0.2914), (0, 0.0086)이 된다. 중심점에서의 반복을 5회로 할 때 전체 실험점은 아래의 표 2와 같다.

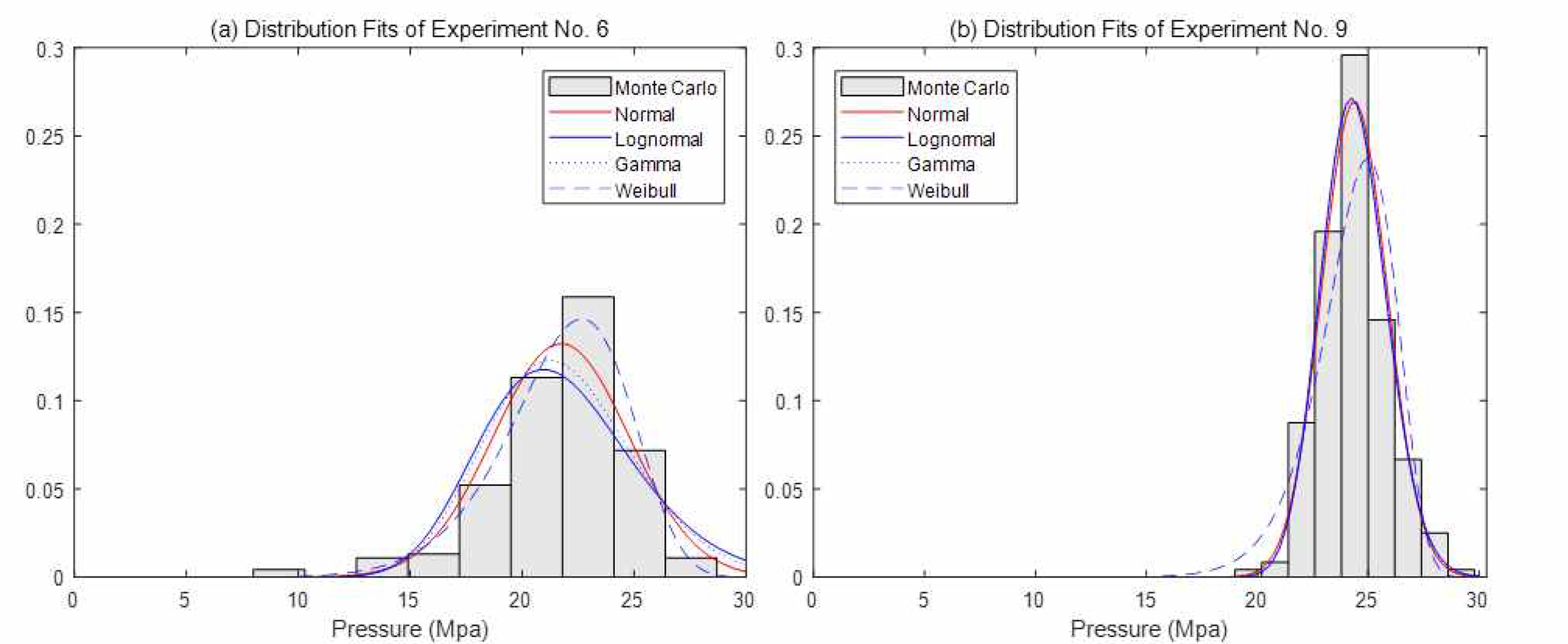
표에는 X₁과 X₂의 실험조건과 함께 이들을 표준화한 U₁과 U₂의 실험조건도 포함되어 있다. 즉 U₁과 U₂는 U₁ = (X₁-0.30)/0.20과 U₂ = (X₂-0.15)/0.10와 같이 구한 것이다. 또한 표 2에는 각 실험조건에서 MCS를 이용하여 생성된 200개의 파열압력 표본을 이용해서 얻어진 표본평균 Y₁과 표본표준편차 Y₂도 수록하고 있다. 앞서 언급한 바와 같이 파열압력은 X₁과 X₂의 COV에 크게 의존하기 때문에 이를 10%, 30%, 50%로 변화시켜가면서 표본을 얻도록 하였다. 예를 들어, 부식 깊이와 길이의 COV를 각각 30%로 설정한 후 가장 최악으로 예상되는 실험조건 6번과 중심점에 대응되는 실험조건 9번에 대한 실험결과를 그래프로 나타내면 아래 그림 6과 같다. 그림에는 정규분포, 대수정규분포, 감마분포, 와이블분포를 이용한 적합 결과를 동시에 보여주고 있다. 두 실험결과 모두 정규분포로 잘 묘사되는 것으로 판단된다. 한편 와이블분포 적합은 분포의 치우침을 보다 적극적으로 수용하는 모습을 보인다.

분석 결과, Y₁과 Y₂에 대한 반응표면 회귀식은 다음과 같이 구할 수 있다.

어떤 부식결함에 대해서 그 깊이와 크기 즉 (X₁, X₂)이 주어지면 상기의 회귀식을 이용하여 해당 파열압력의 분포를 추정할 수 있게 된다. 여기에 운영압력의 분포가 정해지면 배관의 신뢰도를 계산할 수 있다. 그리고 부식성장 예측치가 주어질 때에는 식 (4)와 (5)를 이용하여 시간에 따른 파열압력의 분포를 구할 수 있으므로 배관의 잔여수명 예측이 가능해진다.

제안된 방법의 적용절차를 예시하기 위해 동일한 테스트 구간에서 하나의 부식결함이 검출되었다고 가정하자. 이 결함의 깊이와 길이가 (X₁, X₂) = (0.25, 0.30)라고 할 때 먼저 평균과 표준편차를 추정한다. 이를 위해 식 (4)와 (5)를 이용하면 (Y^1, Y^2)= (20.714, 2.200)를 얻는다. 신뢰도 계산을 위해서는 내부 운영압력에 대한 분포가 필요하다. 공급관리소 측정결과를 분석해서 제안된 값은 평균 6.86Mpa, 변동계수 6%이다. 파열압력과 운영압력이 서로 독립인 정규분포를 따른다고 가정하면 2장에서 설명한 식 (3)을 이용하여 다음과 같이 신뢰도를 구할 수 있다.

이 결과를 고장확률로 나타내면 p^ = 1-R^=3.014×10-10이 된다. ISO 16708:2006(E)는 매설지역의 안전등급에 따라 최대로 허용되는 km당 연간 고장확률을 제시하고 있는 데 우리나라는 대부분 인구밀도가 높은 지역이므로 안전등급 “Very High”를 적용할 경우 고장확률 허용한계는 식 (6)의 산식으로 구할 수 있다.

단, P_op와 D는 내부 운영압력(bar)과 배관 직경(m)을 각각 의미한다. 식 (6)에 P_op = 6.86Mpa = 68.6bar와 D = 0.762m를 대입하면 안전등급 4일 때의 허용한계는 p_lim = 1.647×10^-7과 같이 얻어진다. 따라서 상기의 결함은 매우 안전한 상태에 있다는 결론이 가능하다.

신뢰도 계산에 이어 잔여수명 평가를 수행하려면 우선 부식성장 예측치가 필요하다. 부식성장을 다루기 위해 선형 모델이나 멱함수 모델이 널리 이용된다. 선형 모델이 부식크기를 과대추정하는 경향이 있기 때문에 멱함수 모델이 현실적으로 타당하지만 적절한 파라미터를 추정하는 것이 어렵다는 단점이다(Caleyo et al. 2009, Zhang et al. 2019). 여기서는 예시를 위해 부식이 시간에 선형적으로 매년 0.5%씩 증가하는 것으로 가정하고 잔여수명을 평가하기로 한다.

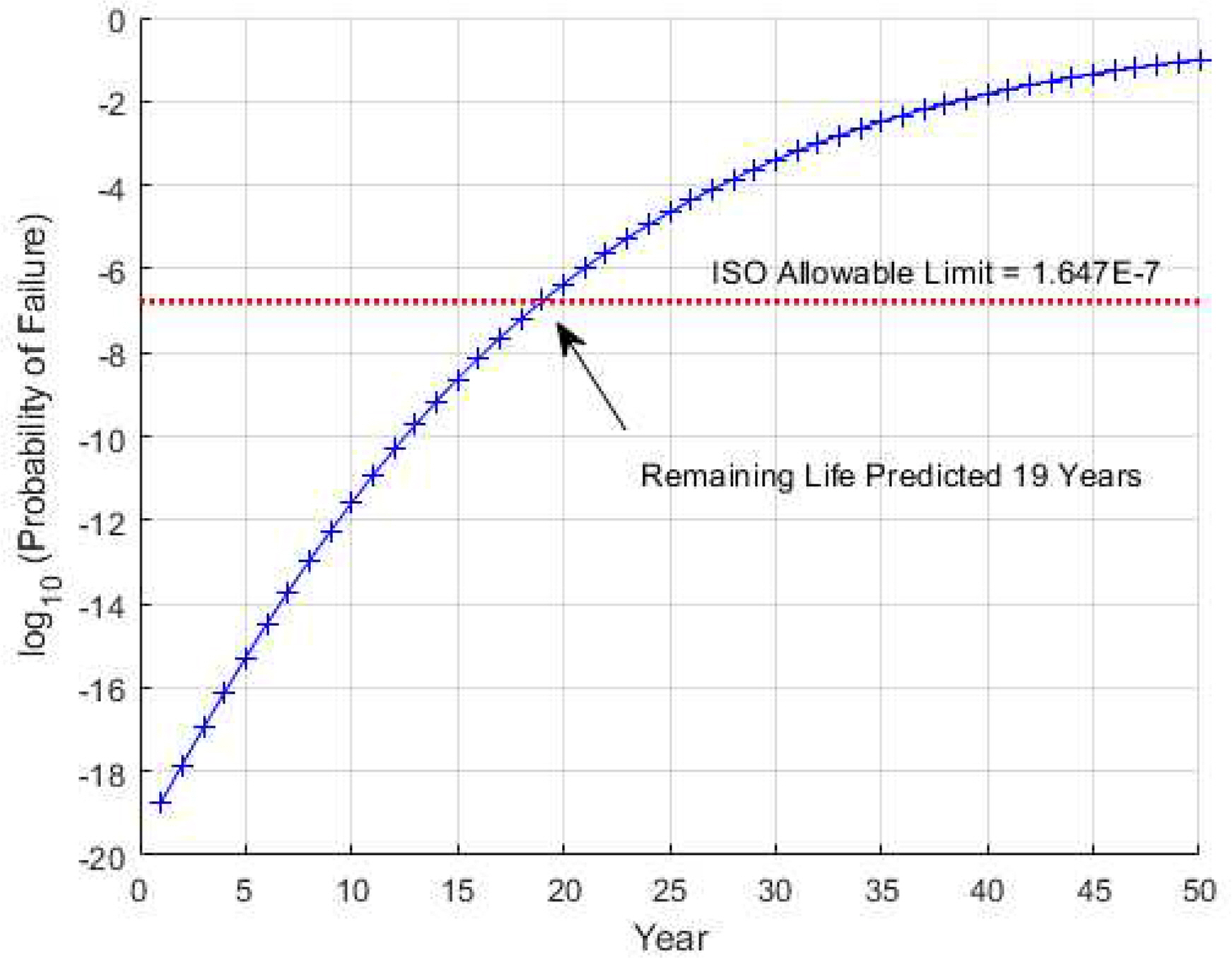
부식성장 예측치가 해마다 주어지면 식 (4)와 (5)를 이용하여 (Y₁, Y₂)을 추정, 신뢰도를 구할 수 있다. 신뢰도 계산값이 1에 가깝기 때문에 고장확률에 로그를 취해서 나타내는 것이 편리하다. 아래의 그림 7은 시간 경과에 따른 고장확률이 점차 증가하고 있음을 보여주고 있다. 고장확률은 약 19년 후에 ISO 허용한계를 초과할 것으로 예상되므로 배관의 잔여수명은 19년이라고 예측할 수 있다. 이 시점에서 예상되는 부식크기는 (X₁, X₂)= (0.345, 0.395)이고 파열압력의 평균과 표준편차는 (Y^1, Y^2) = (19.558, 2.550)으로 추정된다. 지금까지 보인 예시는 부식 깊이와 길이의 COV를 모두 30%로 설정했을 때의 결과이다. 만약 COV를 다른 값으로 설정해야 한다면 다시 실험결과를 얻고 반응표면 회귀식을 도출해야 한다. 신뢰도 및 잔여수명 평가를 위한 적용절차는 동일하다.