 |
 |
AbstractPurposeThis study aims to predict the dry cargo transportation market economy. The subject of this study is the BDI (Baltic Dry Index) time-series, an index representing the dry cargo transport market.
MethodsIn order to increase the accuracy of the BDI time-series, we have pre-processed the original time-series via time-series decomposition and data augmentation techniques and have used them for ANN learning. The ANN algorithms used are Multi-Layer Perceptron (MLP), Recurrent Neural Network (RNN), and Long Short-Term Memory (LSTM) to compare and analyze the case of learning and predicting by applying time-series decomposition and data augmentation techniques. The forecast period aims to make short-term predictions at the time of t + 1. The period to be studied is from '22. 01. 07 to '22. 08. 26.
ResultsOnly for the case of the MAPE (Mean Absolute Percentage Error) indicator, all ANN models used in the research has resulted in higher accuracy (1.422% on average) in multivariate prediction. Although it is not a remarkable improvement in prediction accuracy compared to uni-variate prediction results, it can be said that the improvement in ANN prediction performance has been achieved by utilizing time-series decomposition and data augmentation techniques that were significant and targeted throughout this study.
ConclusionNevertheless, due to the nature of ANN, additional performance improvements can be expected according to the adjustment of the hyper-parameter. Therefore, it is necessary to try various applications of multiple learning algorithms and ANN optimization techniques. Such an approach would help solve problems with a small number of available data, such as the rapidly changing business environment or the current shipping market.
1. 서 론국제무역에서 발생하는 해운 수요를 주요 수익원으로 삼는 해운 경기는 세계 경제 상황과 밀접한 상관관계를 갖는다. 현재 세계 경제는 COVID-19과 재정 긴축으로 인한 경기침체뿐만 아니라, 리쇼어링, 미-중 무역전쟁, 글로벌 공급망 이슈, 등의 복합적인 경기변동 요인들에 의해 불확실성이 확대되고 있다. 이에 정밀한 경기 예측 중요성이 더욱 강조되고 있는 시점이다. 경기 예측이란 장래의 경기변동을 정성/정량적 등의 방법론을 통해 추세를 예측하고 미래에 대한 불확실성을 최소화하는 데 의의가 있다.
본 연구에서는 여러 해운 시장 중 건화물 운송시장에 대한 경기 예측을 목표로 한다. 해당 시장은 원자재를 운송하는 시장 특성상 그 추세가 글로벌 경기에 선행하여 나타나는 것으로 알려져 있다. 연구 대상은 해운 건화물 운송시장 시장을 대표하는 지수인 BDI 시계열이다. 또한, COVID-19 발생 이후 글로벌 경제에 기존과 다른 큰 변곡점이 발생했음을 가정하고 연구 대상 기간과 사용 가능 데이터를 COVID-19 발생 이후의 기간으로 제한하여 ANN을 활용해 BDI를 예측한다. 제한된 가용 가능 데이터가 주어진 상황에서 BDI 시계열 예측 정확도를 높이기 위해 시계열 분해(time-series decomposition) 및 데이터 증강(data augmentation) 기법을 통해 원본 시계열을 전처리(pre-processing)한 후 ANN 학습에 사용한다. 또한 BDI 시계열에 대해 시계열 분해 및 데이터 증강 기법 적용 효과를 규명하기 위해서 선행연구들에서 BDI에 영향을 미치는 것으로 규명된 기타 외생변수는 사용하지 않고 BDI 시계열만을 활용한다. 사용된 ANN 알고리즘은 Multi-Layer Perceptron (MLP), Recurrent Neural Network (RNN), Long Short-Term Memory (LSTM)로 시계열 분해 및 데이터 증강 기법을 적용하여 학습 및 예측을 진행한 경우와 그렇지 않은 경우를 비교·분석한다. 이때의 예측 기간은 t + 1 시점의 단기 예측을 목표로 한다. 연구 대상 시계열 데이터의 기간은 '20. 01. 07부터 '22. 08. 26까지로 총 661일이다.
연구의 흐름은 본 문단 이후 제2장에서 시계열 분해 및 데이터 증강 기법에 대한 이론적 배경 및 관련 선행연구를 탐구한다. 제3장에서는 선행연구를 바탕으로 설정한 연구의 기본가정과 데이터 전처리에 관해 서술한다. 이어서 제4 장에서는 실험 및 실험 결과를 서술하고, 제5장 결론에서는 본 연구의 의의 및 한계점과 추후 연구과제에 대해 논한다.
2. 이론적 배경 및 선행연구2.1 이론적 배경: 시계열 분해 및 데이터 증강 기법2.1.1 시계열 분해 기법시계열 분해란 시계열이 체계적 성분(systematic component)과 불규칙적 성분(random component)으로 이루어져 있다는 가정하에 각각의 성분을 시계열로부터 분리하는 기법이다. 체계적 성분은 계절(seasonality) 성분, 추세(trend) 성분, 순환(cyclicity) 성분으로 구분된다. 시계열 예측에 대해 분해 기법을 적용하는 의의는 다음과 같다. 첫 번째, 시계열 자료를 분해된 성분별로 분석할 수 있다. 시계열 자료로부터 각 성분을 분리하여 장기적 추이를 분석하고 불규칙성이 발생한 시점을 검증할 수 있다. 두 번째, 계절조정(seasonal adjusted) 자료를 얻을 수 있다. 체계적 성분 중 계절적 성분은 시계열의 장기 변동성 분석에 노이즈로 작용하여 분석 예측력을 떨어뜨린다. 이때 시계열 분해를 적용하여 원본 시계열 데이터로부터 계절 성분과 불규칙적 성분을 분리해냄으로써 모델의 분석 예측력 또는 정확도를 높일 수 있다. 해당 방법론의 적용과 계산은 단순하고 직관적이어서 통계 방법론 등의 다양한 연구들에 활용되고 있다. 시계열 분해는 적용 대상 시계열 데이터의 특성 등에 따라 활용할 수 있는 여러 모형이 존재한다. 하지만 기본적으로 시계열 분해 모델들은 크게 가법(additive) 모형과 승법(multiplicative) 모형으로 나눌 수 있다. 각 모형의 수식은 다음과 같이 차례대로 식(1)과 식(2)로 나타낼 수 있다.
두 모형 모두 체계적 성분과 불규칙적 성분으로 시계열을 분해하는 것은 같으나, 가법 모형의 경우 분해된 변수 간의 단순 덧셈으로 나타내어 계절 변동의 크기 또는 추세 주기의 변동이 시계열의 진폭에 따라 변하지 않는 특성을 띠는 데이터에 적절한 분해 모형이다. 반대로 승법 모형의 경우 계절 패턴과 추세 주기의 변동이 시계열의 수준에 따라 비례하여 변화하는 특성을 띠는 데이터에 적절한 분해 모형이다. 일반적으로 비즈니스 또는 경영·경제 분야에서 활용되는 데이터들은 비선형성을 띠는 데이터들이 대부분이다. 본 연구의 대상이 되는 해운 경기 지수도 여타 경기 지수와 마찬가지로 비선형성을 띠므로 해당 데이터 특성에 적합한 시계열 분해 승법 모형을 활용한다. 본 연구에서 사용한 시계열 분해 기법에 대한 자세한 설명은 제3장 데이터 전처리에서 서술한다.
2.1.2 데이터 증강 기법데이터 증강 기법은 기계학습(Machine Learning) 알고리즘의 학습을 위해 풍부한 데이터를 제공함으로써 학습 정확도를 높이고 과적합(over-fitting)을 방지함으로써 ANN 모델이 학습하지 않은 패턴 또는 데이터(unseen data)에 대해서도 강건성(robustness)을 높일 수 있는 기법이다. 오늘날의 기계학습은 딥러닝(Deep Learning)으로 발전하면서 매개변수가 수만 개 이상에 이르러 모델 복잡도가 높아지게 됐다. 반면에 학습에 사용할 수 있는 데이터의 수는 부족한 경우가 많아 모델 과적합의 위험은 증가했다. 이를 해결하기 위해 다양한 기법들이 적용되는데, 대표적으로 drop-out, L1 / L2 regularization, early stopping 등이 있다. 해당 기법들은 ANN의 과적합을 예방하고 학습된 모델의 일반화(generalization) 성능을 높일 수 있는 장점이 있다. 하지만 이는 여전히 ANN 모델 자체의 hyperparameter는 줄일 수 있을지언정 해당 기법들의 적용을 위해 추가적인 변수들의 조정이 필요해지며 상황에 따라 특정 기법의 사용이 제한되는 경우가 많다. 또한, ANN은 black-box 모델이라는 한계점이 존재하므로 해당 기법들의 적용이 ANN 모델의 학습 간에 어느 정도의 영향을 미치는지 연구자가 실시간으로 파악하기 어렵다. 이와 같은 현실적인 한계점을 극복하고자 하는 여러 방면의 시도 중의 하나가 학습에 사용되는 데이터를 늘리는 방법이다. 기계학습 또는 딥러닝의 학습 데이터를 늘리는 방법으로는 크게 1. 더 많은 소스로부터 더 많은 데이터를 수집, 2. 인위적인 데이터 합성 또는 생성(e.x. Generative Adversarial Network: GAN), 3. 데이터 증강 기법 활용 등이 있다. 1번 방법의 경우 현실적으로 수집할 수 있는 데이터가 한정적이라는 점뿐만 아니라, 시계열 데이터의 경우 데이터의 양이 연구 대상 기간으로 제한된다. 2번 방법의 경우 GAN을 위해 추가적인 ANN 모델을 학습시켜야 하므로 컴퓨팅 비용과 모델 복잡도가 증가한다. 또한, 확률론적 기반으로 데이터를 생성해내기 때문에 센서 데이터 또는 신호처리 및 공학 분야가 아닌, 비즈니스 또는 경영·경제 분야에는 적용이 어렵다. 특히, 시계열 데이터의 분류(classification)가 아닌 예측(forecasting)을 위해 해당 방법론을 접목하기에는 시계열 데이터의 시간 의존성(time dependency)이란 특성 때문에 여러 한계점이 있다. 본 연구에서는 연구 대상 데이터 특성에 가장 적합한 3번의 방법인 데이터 증강 기법을 활용해 연구를 진행한다.
데이터 증강 기법 역시 GAN의 경우와 마찬가지로 기존의 데이터를 이용해 새로운 데이터를 만들어 낸다. 하지만 GAN의 경우 비지도 학습(unsupervised learning)을 통해 실제 데이터와 비슷한 확률분포를 가지는 가상의 데이터를 새롭게 생성해내지만, 시계열 데이터에 주로 활용되는 데이터 증강 기법들은 사용자가 정의하는 통계 분포의 범주 또는 노이즈의 추가에 따라 원본 데이터가 가진 특성을 보존하는 선에서 추가적인 데이터를 생성해낸다는 차이점이 있다. 물론 GAN도 넓은 의미에서는 추가적인 데이터를 생성해낸다는 점에서 데이터 증강 기법의 특수한 형태로 보는 관점의 연구들도 있다. 본 연구의 연구자도 해당 논거에 일부분 동의한다. 하지만 이에 관한 추가적인 논의는 본 연구의 논지와 벗어나므로 자세한 내용은 관련 분야의 리뷰 논문인 Wen et al.(2020)의 연구를 참고할 수 있다. 본 연구에서 사용한 데이터 증강 기법에 대한 자세한 설명은 제3장 데이터 전처리에서 서술한다.
2.2 선행연구: 시계열 분해 및 데이터 증강 기법 활용 인공신경망 응용 연구2.2.1 시계열 분해 기법 활용 인공신경망 응용 연구ANN을 활용한 시계열 예측의 정확도를 높이기 위해 시계열 분해 기법을 적용한 다양한 연구 사례들이 있다. Ina et al. (2015)의 연구에서는 신호처리 분야에서 사용되는 시계열 분해 기법의 하나인 이산 웨이브릿 변환(Discrete Wavelet Transform)을 통해 연구 대상 시계열의 선형성과 비선형성을 분리했다. 선형성을 갖는 시계열은 Autoregressive Integrated Moving Average (ARIMA)릍 통해 예측하고 비선형성을 갖는 시계열의 경우는 ANN을 통해 각각 예측하는 하이브리드(hybrid) 모형을 제시하며 해당 연구의 모티브가 된 연구인 Zhang (2003)의 연구보다 우수한 예측 결괏값을 보여줌을 증명했다. 저자는 해당 연구에서 선행연구들을 근거로 시계열을 분해하고 선형성과 비선형성으로 나타나는 각각의 데이터 특성에 적합한 분석 모델을 적용함으로써 예측 정확도를 높일 수 있다고 주장하고 있다. 이외에도 일반적인 형태의 시계열 분해 기법을 적용한 데이터를 ANN의 학습자료로 활용한 시계열 예측연구들이 있다. Hansen & Nelson (2013)은 선행연구를 근거로 체계적/불규칙적 성분으로 시계열을 분해하는 일반적인 형태의 시계열 분해 기법이 이론과는 달리 경제, 비즈니스 운영 등의 실증 데이터에 대해 저조한 예측력을 보인다고 주장했다. 저자는 해당 현상의 원인은 시계열 분해 기법이 과거에 연구되어 최근의 데이터에는 적합하지 않다는 점, 원본 시계열 데이터로부터 분해된 노이즈는 일반적인 통계적 예측기법에서는 무시되는 경향이 있으나 해당 데이터가 중요한 정보를 포함하고 있을 수 있다는 점, 그리고 일반적인 시계열 분해 기법에서 사용되는 가법 모형과 승법 모형이 최적 해법이 아닐 수 있다는 점 등을 이유로 들고 있다. 이에 저자는 ANN을 통해 해당 한계점을 극복하고 예측 정확도를 향상할 수 있다고 주장하고 있다. 특히 시계열 분해 기법을 통해 도출되는 체계적 성분들은 데이터 특성상 시간의 흐름에 따라 변화하는 추세를 띄고 있어서 ANN의 학습 능력이 해당 데이터를 다루는 데 적합하다고 기술하고 있다. 이 외에도 시계열 분해 기법으로 전처리한 데이터를 다양한 ANN 모델을 활용해 시계열 데이터 예측의 정확도 제고를 시도해 유의미한 결괏값을 도출한 여러 연구가 있다(Lin et al. 2021; Méndez-Jiménez & Cárdenas-Montes 2018). 본 연구와 유사하게 원자재 분야에서 ANN을 활용한 시계열 예측의 정확도를 높이기 위해 시계열 분해 기법을 적용한 연구 사례로 Abdollahi (2020)의 연구가 있다. 해당 연구는 Complete Ensemble Empirical Mode Decomposition (CEEMD)를 활용해 유가를 Intrinsic Mode Functions (IMFs)로 분해한 뒤 다양한 hybrid ANN 모델을 통해 예측했다. 그 결과로 해당 연구에서 제안하는 방법론들의 조합이 기존의 방법론보다 우수함을 증명했다. 또한, 선행연구들에서 주요 연구 대상이 돼왔던 신호처리 분야뿐만 아니라, 유가 예측과 같은 주요 경제지표 예측연구 분야에서도 시계열 분해 기법을 활용함으로써 ANN의 학습 단계에서 시계열의 변동성을 더욱 잘 학습시키는 데 도움이 될 수 있다고 밝혔다.
반대로 시계열 분해 기법이 ANN 학습 시 유의미한 차이를 보이지 않는다고 나타난 연구 결과도 있다. Benkachcha et al. (2015)의 연구에서는 일반적인 시계열 분해 기법을 통해 시계열 데이터를 체계적 성분과 불규칙적 성분으로 분해했다. 그 후 분해한 모든 데이터를 ANN에 학습 데이터로 사용하여 분해 데이터를 학습에 사용한 경우와 아닌 경우의 결괏값을 비교했다. 해당 문헌의 경우 ANN의 예측 정확도를 평가하는 일반적인 지표를 통해 각각을 비교한 값을 제시하지 않고 그래프만을 도식한 결괏값을 제시하고 있다. 이 때문에 수치를 통한 객관적인 비교는 어렵지만, 저자의 주장에 따르면 ANN을 학습하는 데 사용되는 모델 복잡도 등의 효율성 비용을 고려하면 연구 대상 시계열에서는 시계열 분해 기법을 사용하지 않는 편이 낫다고 주장했다. 해당 연구와 유사하게 Ouyang et al. (2021)의 연구에서는 STL 시계열 분해 기법으로 여러 분야의 시계열 데이터를 전처리한 후 각각 ARIMA과 Error, Trend, Seasonal (ETS) 모델 등의 고전적인 통계 방법론, 그리고 다양한 기계학습 및 ANN 알고리즘을 통해 예측 정확도를 비교했다. 그 결과 통계 방법론이 가장 우수한 결괏값을 나타냈으며, 기계학습 알고리즘의 경우 통계 방법론보다 저조한 결괏값을 보이지만 기계학습에 활용되는 여러 전처리 및 최적화 기법들을 적용하여 성능을 개선할 수 있다고 주장했다. ANN 알고리즘 역시 통계 방법론에 비해 저조한 결괏값이 도출되었지만, 해당 연구에서는 2가지 모델만을 활용했기에 최적의 해법이 도출되지 않았음을 연구의 한계점으로 언급했다. 또한, 해당 분야는 활발하게 연구되고 있는 만큼 개선된 알고리즘 또는 하이브리드, 앙상블(ensemble) 모델, hyperparameter 조정 등을 통해 더 나은 결괏값을 도출해낼 수도 있다고 밝혔다.
상기에 서술한 선행연구들은 특정 시계열에 한정된 연구일뿐만 아니라, 시계열 데이터와 ANN의 특성상 시간 변화에 따라 학습 결괏값이 달라질 수 있다. 따라서 시계열 분해 기법이 ANN 학습에 불필요하거나 의미가 부족하다는 주장은 다소 논리의 비약이 존재한다. 기본적인 ANN은 주어진 데이터로부터 해 공간(solution space)을 탐색하여 투입-산출 데이터 간의 오차 값을 최소화할 수 있는 가중치로 이루어진 방정식을 근사(approximation)하는 방법론이다. 이와 같은 알고리즘 특성으로 인해 ANN은 black-box model이라 불리기도 하는 만큼 학습 과정에서 어떠한 이유로 해당 결괏값이 나오는지, 또 학습 결과로 표현되는 가중치의 조합들이 무엇을 의미하는지 알 수 없다. 이같이 ANN은 모델 복잡도와 특성에 따른 한계점이 분명하지만, 현대 컴퓨팅 파워의 비약적인 발전과 학습 가능 데이터의 증가, 그리고 개선된 응용 알고리즘들의 개발 등으로 인해 많은 분야에서 활용되고 있다. 또한, Ouyang et al. (2021)에서도 해당 연구의 결괏값은 ANN 모델의 조정(tuning)을 통해 성능 개선의 여지가 있다고 언급한 만큼 다양한 데이터에 대해서 여러 종류의 접근법을 시도해볼 학술 가치가 충분하다.
2.2.2 데이터 증강 기법 활용 인공신경망 응용 연구ANN을 활용한 시계열 예측의 정확도를 높이기 위해 데이터 증강 기법을 적용한 다양한 연구 사례들이 있다. Si Lee & Kim (2020)의 연구에서는 ANN을 활용한 주식 시장 주가 예측 성능 향상을 위해 기계학습과 ANN 알고리즘의 학습에 있어서 풍부한 데이터양의 중요성을 강조하며 Column-wise random shuffling이라는 데이터 증강 기법을 제안했다. 해당 기법을 통해 전처리된 데이터를 ANN 모델을 통해 다양한 주식 시장에 대한 예측을 시행한 결과 유사 선행연구들에 대비해서 평균 약 51.813%의 Mean Squared Error (MSE)의 오차율 감소를 달성했다. Sumeyra et al. (2021)의 연구는 데이터 증강 기법으로써 Auto Encoder (AEs), Variational Auto Encoders (VAEs), 등의 ANN 알고리즘을 사용해 벨기에와 네덜란드의 전기요금 시계열 데이터를 전처리했다. 그 후 통계적 회귀 방법론인 Seasonal ARIMA (SARIMA)와 ANN을 사용하여 각각 예측 후, 데이터 증강 기법이 적용된 실험과 미적용된 실험 간의 결괏값을 비교·분석했다. 결과로 해당 연구에서 사용된 각각의 데이터 증강 기법은 약 2.64%의 ANN 예측 정확도 향상에 도움이 되었다. 또한, 해당 연구에서 상기에 열거한 데이터 증강 기법들을 조합하여 적용한 실험에서는 동일 시계열 데이터에 대해서 최대 약 3.44%의 ANN 예측 정확도 향상률을 보였다. 해당 연구를 통해 실무 또는 연구에서 부족한 데이터 수를 늘리고 ANN의 예측 정확도 향상을 위해 다양한 데이터 증강 기법을 적용해보는 것이 유의미한 시도임을 알 수 있었다. 딥러닝 알고리즘이 현실 세계에서 활용할 수 있는 정도의 학습 수준에 도달하기 위해서는 학습 데이터에 대한 과적합을 방지하고 학습된 모델의 일반화(generalization) 성능을 강화해야 한다. 이를 위해선 풍부한 양의 데이터를 학습시키는 것이 필수이다. Wen et al. (2020)은 ANN의 학습 간에 다량의 데이터에 대한 필요성을 강조하며 이를 충족하고자, 다양한 분야에서 데이터 증강 기법의 적용을 시도하는 연구가 이루어지고 있다고 밝혔다. 하지만 기계학습 또는 딥러닝 분야에서 해당 기법의 적용을 시도한 연구들은 이미지 분류(classification)에 치중되어있음을 지적하며 시계열 분야에 연구가 상대적으로 부족한 이유를 다음과 같이 정리하고 있다. 첫 번째, 현재까지 개발된 시계열 증강 기법으로는 시계열 데이터의 내재 된 속성을 온전히 나타낼 수 없다. 이미지 데이터와는 달리 시계열 데이터는 시간의 흐름에 따라 각각의 데이터가 시간 의존성을 띠기 때문이다. 두 번째, 대부분의 데이터 증강 기법은 특정 형태의 데이터에 한정적으로 적용되어 범용성이 떨어진다. 예를 들어 이미지 croping은 이미지 처리에 유효한 데이터 증강 기법으로 이를 시계열 데이터에 그대로 적용하여 숫자를 croping하는 경우에는 해당 시계열 데이터가 가진 성질을 무시하고 의미 없는 데이터를 만들어 내기 때문이다. Oh et al. (2020)은 인공지능 학습의 이미지 처리에서 주로 활용되는 데이터 증강 기법을 시계열 데이터에 적용하는 방안을 연구했다. 해당 기법은 인공지능의 이미지 처리와 학습을 위주로 연구되어 왔기 때문에, 시계열 학습에 대해서는 해당 분야에서 만큼의 뛰어난 성능은 보이지 않는다고 했다. 하지만 현실 세계의 시계열 데이터는 인공지능 학습에 활용할 수 있을 만큼, 풍부하지 않기 때문에 해당 기법을 통해 학습 데이터를 증가시키기 위한 지속적인 연구가 필요하다고 주장했다.
본 연구의 저자도 선행연구들의 의견에 전적으로 동의한다. 특히 BDI 시계열의 경우 COVID-19 이후의 경기변동으로 인해 해당 시계열이 이전 시점의 데이터와 다른 추세를 보인다고 가정할 경우, 이전 시점의 데이터는 ANN 학습에 활용이 제한된다. 따라서 COVID-19 이후의 짧은 기간을 대상으로 한 연구에서 한정적인 기간의 데이터만으로 ANN 예측을 시도하기 위해선 데이터 증강 기법의 적용이 필수적이다.
3. 데이터 전처리 및 기본가정본 연구에서는 COVID-19 발병 이후의 글로벌 경제, 특히 해운 경제 분야 수요공급 데이터의 추세 및 내재(intrinsic) 된 성질이 이전과는 다른 양상을 띨 것이란 가정을 전제로 한다. 따라서 ANN 학습 때 해당 시점 이후의 제한적인 기간의 데이터만을 사용하되 ANN 학습 알고리즘의 특성에 따른 학습 능력을 재고하기 위해서 시계열 분해와 데이터 증강 기법으로 전처리한 데이터를 활용한다. 단, 시계열 분해와 데이터 증강 기법의 효과성을 명확히 검증하기 위해 BDI 시계열 및 전처리한 데이터를 제외한 기타 외생변수는 사용하지 않는다. 전처리 데이터를 사용하지 않은 경우는 단변량 시계열 예측 문제이며, 사용한 경우는 다변량 시계열 예측 문제이다. 즉, 단변량의 경우 BDI 시계열 데이터만을, 다변량의 경우 BDI 시계열 데이터를 시계열 분해 기법을 통해 전처리한 seasonal, trend, re- mainder 데이터 세트와 데이터 증강 기법을 통해 전처리한 jittering, scaling 데이터 세트가 ANN의 학습 데이터가 된다.
ANN의 예측단계에서는 t + 1 시점의 예측을 목표로 한다. 이를 위해서 데이터 전처리시 t - 1 시점의 입력 데이터와 t 시점의 출력 데이터를 매칭하여 학습이 완료된 ANN에 t 시점의 데이터 입력 시 t + 1 시점의 데이터가 예측값으로 출력되게 한다. 연구 대상 기간은 WHO (World Health Organization) 기준 공식 첫 확진자가 발병한 '22. 01. 051) 이후의 기간으로 설정한다. 주말, 공휴일을 제외한 실제 연구 대상 시계열 데이터의 기간은 '20. 01. 07부터 '22. 08. 26까지로 총 661일이다. 시계열의 주기는 일간 단위이며, ANN의 학습과 예측 역시 일간 단위로 이루어진다. 데이터는 Clarkson 社의 Shipping Intelligence Network2)에서 제공하는 BDI 시계열 데이터를 사용한다. 연구 대상 기간의 BDI 시계열은 Figure 1.에 나타냈다.
선행연구를 통해 BDI 시계열 예측에 적합한 시계열 분해 및 데이터 증강 기법을 선정했다. 시계열 분해 기법의 경우 Cleveland et al. (1990)이 제안한 Seasonal and Trend decomposition using Loess (STL)을 활용한다. 해당 모형은 Locally Estimated Scatter plot Smoothing (Loess)를 응용한 시계열 분해 기법이다. Loess 또는 local regression은 데이터 전체를 여러 구간으로 구분하여 각각의 데이터 세트에 대해서 최소자승회귀(least squares regression)를 반복하여 시계열을 평활화(smoothing)하는 비모수적 접근법이다. STL은 R Programming의 패키지인 Hafen (2016)의 ‘stlplus’를 활용한다. 해당 시계열 분해 기법의 특징에 따른 장단점은 다음 Table 1.에 나타냈다.
STL은 Local Regression을 활용하여 시계열을 평활화한 뒤 각각을 더해주는 가법 모형의 형태를 띠고 있어 승법 형태의 시계열 분해를 수행할 수 없다. 이를 승법 형태의 시계열 분해로 변환하기 위해서는 원본 데이터를 로그 변환해 준 뒤 STL 모델로 분해하여 얻을 수 있다. 따라서 본 연구에서는 로그 변환된 원본 데이터를 STL 분해 기법으로 분해한 뒤, 다시 원본 스케일로 되돌리기 위해 로그함수의 역함수인 지수함수로 처리한다. 분해된 시계열은 다음 Figure 2.에 나타냈다.
데이터 증강 기법의 경우는 Iwana et al. (2021)의 연구를 참고하여 scaling과 jittering을 사용한다. Scaling은 랜덤 스칼라 값(scalar value)을 원본 데이터에 곱해줌으로써 전체 시계열의 진폭을 조정하는 기법이다. 적정 크기의 무작위 값을 곱하기도 하나, 본 연구에서는 원본 시계열 데이터가 표준분포를 따른다는 가정하에 Gaussian distribution α ~ N(1, σ2)에 속하는 값으로 스칼라 값 α를 설정한다. 선행연구를 참고하여 평균 μ = 0과 표준편차 σ = 0.2로 분포를 설정하여 원본 데이터에 scaling 처리를 진행했다. Figure 3. 상단 그래프는 scaling을 위해 설정한 평균과 표준편차에 따라 생성된 데이터이다. 하단 그래프는 BDI 시계열 원본 데이터에 scaling으로 생성된 데이터를 곱연산하여 처리해준 그림이다. Scaling 증강 기법의 수식은 식(3)으로 나타낼 수 있다.
Jittering은 원본 데이터에 노이즈를 더해줌으로써 ANN 학습 과정에서 이상치(outlier)에 대해 모형의 강건성을 높이고 완성된 모형의 일반화(generalization) 성능의 향상을 기대할 수 있다. 해당 기법도 마찬가지로 원본 시계열 데이터가 표준분포를 따른다는 가정하에 Gaussian distribution ε ~ N(1, σ2)에 속하는 값으로 스칼라 값 α를 설정한다. 선행연구를 참고하여 평균 μ = 0과 표준편차 σ = 0.0으로 분포를 설정하여 원본 데이터에 jittering 처리를 진행했다. Figure 4. 상단 그래프는 jittering을 위해 설정한 평균과 표준편차에 따라 생성된 데이터이다. 하단 그래프는 BDI 시계열 원본 데이터에 jittering으로 생성된 데이터를 합연산하여 처리해준 그림이다. Jittering 증강 기법의 수식은 식(4)로 나타낼 수 있다.
본 연구에서 사용한 모든 데이터는 스케일의 편차가 크므로 ANN 모형들의 학습을 보장하기 위해 min-max nor- malization으로 전처리한 뒤 학습에 사용한다. 분해된 시계열 데이터는 지수함수로 처리해서 원복한 뒤 다른 데이터들과 마찬가지로 min-max normalization으로 전처리하여 ANN 학습에 사용한다. 시계열 데이터에 적용되는 min-max normalization은 다음 식(5)와 같이 나타낼 수 있다.
시계열 분해 및 데이터 증강 기법의 적용이 ANN을 활용한 BDI 시계열 예측 정확도에 미치는 영향을 비교분석 하기 위해 학습된 ANN 모델의 성능을 평가하는 지표들로 선행연구들을 참고하여 Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE), Symmetric Mean Absolute Percentage Error (SMAPE)를 사용한다. MAPE는 0~100% 범주의 값으로 나타나며 0에 가까울수록 학습 결과의 정확도가 높음을 의미한다. 모델의 예측값과 실제값의 차이에 절댓값을 취해줌으로써 실제값의 크기에 의존해서 나타나는 에러 값을 처리하는데 용이하다. RMSE는 Mean Square Error (MSE)와 달리 전체 수식에 제곱근 처리를 함으로써 오차값 차이가 크면 클수록 큰 페널티를 주는 이점이 있어 평균치에서 크게 벗어나는 오차율의 처리에 대해 유리하다. 해당 값 역시 수치가 낮게 나타날수록 학습 결과의 정확도가 높음을 의미한다. SMAPE는 MAPE의 수식에 절댓값 형태의 예측값
본 연구에서 사용된 ANN 모델은 Multi-Layer Perceptron (MLP), Recurrent Neural Network (RNN), Long Short-Term Memory (LSTM)이다. ANN의 학습과 예측은 모두 R Programming에서 패키지 개발자들이 제공하는 패키지를 활용한다. 사용된 패키지는 Fritsch et al. (2019)의 ‘neuralnet’, Quast (2022)의 ‘rnn’, Kalinowski et al. (2022)의 ‘keras’, Falbel et al. (2022)의 ‘tensorflow’ 등이다. LSTM의 경우 ‘tensorflow’ 패키지를 backend로 사용하여 ‘keras’로 학습을 진행한다. MLP는 ANN의 최소 구성단위인 퍼셉트론(perceptron)을 은닉층(hidden layer)을 포함한 세 개 이상의 층(layer)으로 구성한 모델로 XOR 문제나 기타 복잡한 문제를 해결을 가능케 한 모델이다. RNN은 순환신경망의 기본 모델로 이전 학습 시점의 출력층의 값을 다음 학습 시점의 입력층의 값으로 전달하는 상황 유닛(context unit)이 독립적으로 존재한다. 해당 모델의 학습 알고리즘은 재귀함수의 구조를 띠고 있어 과거의 가중치를 미래의 가중치에도 영향을 미치게 함으로써 ANN 알고리즘의 장기 기억력을 비약적으로 향상할 수 있었다. 해당 모델의 장점 덕분에 데이터 간의 인과성 또는 연속성을 갖는 자연어 처리, 시계열 예측 등의 데이터 분석에 활용되고 있다. LSTM은 RNN 학습 알고리즘의 한계점인 ‘기울기 소실 또는 발산 문제(vanishing or exploding gradient problem)’를 개선한 모델이다. 기존의 RNN에 셀(cell)과 게이트(gate)의 개념이 추가되며 기울기 소실 또는 발산 문제를 억제하면서도 순환신경망 모델의 장기 기억력을 증대시켰다. 본 연구에서 활용한 모든 ANN 모델은 알고리즘 등의 변형 없이 기본 모델을 사용한 만큼 세부 수식과 학습 알고리즘에 대한 나열은 생략한다. 모든 모형에는 early stopping rule을 추가하여 모델의 학습이 완료되었을 때 테스트 데이터에 대해서 발생할 수 있는 과적합을 방지한다. ANN 모델의 학습, 검증, 테스트 데이터 세트의 비율은 70%, 15%, 15%로 진행한다. 연구 대상 시계열 데이터의 기간은 '20. 01. 07부터 '22. 08. 26까지로 총 661일이다. 학습 데이터 세트의 기간은 '20. 01. 07 ~ '21. 11. 02이고 검증 데이터 세트의 기간은 '21. 11. 03 ~ '22. 03. 30이며 테스트 데이터 세트의 기간은 '22. 03. 31 ~ '22. 08. 25이다.
4. 실험 및 실험결과본 장에서는 3장의 데이터 전처리 및 연구의 기본가정을 바탕으로 ANN의 학습과 t + 1 시점의 시계열 예측을 진행했다. ANN 모델별 층(layer)과 노드(node) 등의 hyperparameter 조정은 본 연구와 유사한 연구(Han & Yu, 2019)를 참고하여 trial and error에 따라 학습을 반복하며 모델 복잡도의 향상에 비해, 예측 정확도가 유의미하게 향상을 보이지 않을 때까지 반복했다. LSTM의 경우 Kang, Cho, & Na (2021)의 연구에서와 마찬가지로 적정 윈도우 사이즈를 탐색하여 모델의 예측 성능 향상을 꾀하는 방법도 있지만, 본 연구에서는 LSTM뿐만 아니라 여타 ANN 모델별 정확한 성능 비교를 위해 모든 ANN 모델들의 학습에 대해서 t - 1의 sliding window 조정만을 통해 학습을 진행했다. 이에 따라 최종 결정된 각 ANN 모델별 구조는 실험을 위해 설정한 주요 hyperparameter와 함께 다음 Table 2.에 나타냈다.
학습된 각 ANN 모델에 테스트 데이터를 대입하여 도출한 예측 성능지표의 결괏값은 Table 3.에 소수점 셋째 자리를 최소 단위로 반올림하여 나타냈다. 해당 내용에 따라 단변량과 다변량 예측의 결과를 비교하면 MLP의 경우 MAPE (%) 약 0.186%, SMAPE (%) 약 0.216%의 향상률을 보여준다. 반면에 RMSE의 경우 (-)1.729%로 다변량 예측이 되려 낮은 예측 정확도를 보여준다. 이는 다변량 예측이 단변량 예측의 경우보다 원본 데이터와 예측치 간 오차값의 평균치와 차이가 큰 값들이 많기 때문으로 해석할 수 있다.
RNN의 경우 MAPE (%) 약 0.081%, SMAPE (%) 약 0.092%의 향상률을 보여주고 있다. 선행연구들에 따르면 순환신경망 알고리즘을 기반으로 하는 RNN과 LSTM은 자연어 처리, 악보 생성, 시계열 예측 등의 연속성을 띠는 데이터들에 대해서 일반적으로 우수한 성능을 보여주는 것으로 알려져 있으나, 본 연구에서는 단변량 및 다변량 예측 모두에서 RNN이 MLP보다 약 0.505%(본 연구에서 사용한 모든 성능지표의 평균) 낮은 정확도로 나타났다. 이 같은 결과는 ANN의 특성에 따라 크게 두 가지의 이유를 유추해볼 수 있다. 첫 번째 일반적인 MLP 모델과 비교해 RNN의 높은 모델 복잡도에 따라 추가적인 hyperparameter의 튜닝을 통해 예측 성능 개선의 여지가 있다는 점, 두 번째 ANN 모델의 복잡도가 높아질수록 더 많은 양의 학습 데이터가 필요하다는 점 등을 생각해 볼 수 있다. RNN의 RMSE도 MLP의 경우와 마찬가지로 다변량 예측이 되려 낮은 예측 정확도인 (-)3.015%로 나타났다.
LSTM은 단변량 예측에 대비 시계열 분해 및 데이터 증강 기법을 적용한 다변량 예측에서 세 가지 ANN 모델 중 가장 높은 예측 성능 향상률을 보여주고 있다 (MAPE (%) 약 0.477%, SMAPE (%) 약 0.514%). 특히, 다른 ANN 모델과 달리 LSTM 다변량 예측의 RMSE 향상률은 15.978%로 괄목할만한 결과를 보여주고 있다. 이는 다변량 예측이 단변량 예측의 경우보다 원본 데이터와 예측치 간 오차값의 평균치와 차이가 큰 값들이 다른 ANN 모델보다도 적기 때문으로 해석할 수 있다. 또한 LSTM은 본 연구에서 사용한 세 개의 ANN 모델 중 유일하게 모든 성능지표에서 성능 향상을 보여준 모델이다. LSTM의 경우 보다 고차원의 ANN 모델로서 알고리즘의 특성상 연속적으로 발생하는 과거 데이터에 대한 추론(inference) 능력이 상대적으로 더 뛰어나기 때문에 다량의 학습 데이터를 투입하여 학습을 진행한 경우가 더 높은 정확도를 보여주고 있음을 알 수 있다. 하지만 예측 성능지표의 기준이 아닌, ANN 모델 간의 성능을 비교하면 MLP, LSTM, RNN의 순서로 높은 예측 정확도를 보여주고 있다. 또한, 시계열 데이터를 예측했음에도 연속성을 띠는 데이터 예측에 우수성을 보인다고 알려진 LSTM보다 MLP가 RMSE를 제외한 기타 성능 평가 지표상에서 가장 높게 나타났다. 이 같은 결과는 ANN이 가지는 black-box 모델의 특성상 정확한 원인을 파악할 수 없다는 한계점이 있다. 단, 확실한 것은 ANN 알고리즘을 활용한 패턴 탐색과 예측 등의 문제해결에서 일정 수준 이상의 성능을 위해서는 보다 대량의 데이터에 대한 ANN의 학습이 필수적이다. 본 연구에 사용된 모델들의 복잡도를 고려했을 경우 MLP의 구조가 상대적으로 간단하여 적은 양의 데이터로도 학습 데이터에 대한 일반화(generalization)가 더 높은 수준으로 이루어진 것이다. 따라서 LSTM이 보여주는 결괏값에 대한 해석도 앞서 RNN에 대한 결괏값의 경우와 마찬가지로 일반적인 MLP 모델과 비교해 LSTM의 모델 복잡도의 증가에 따라 추가적인 hyperparameter의 튜닝을 통해 예측 성능 개선의 여지가 있다는 점과 높아진 모델 복잡도에 따라 더 많은 양의 학습 데이터가 필요하다는 것을 유추해 볼 수 있다. 해당 논지를 뒷받침하는 선행연구들로 특정 시계열들에 한정된 연구 결과이긴 하나, 단순한 구조를 띠는 MLP가 시계열의 특징을 더 잘 나타내는 경우의 연구 결과가 있다(Gers, Eck, & Schmidhuber 2002; Oliveira et al. 2021). 신호 공학 분야에 ANN의 접목을 시도한 Gers, Eck, & Schmidhuber(2002)의 연구에서는 이를 극복하기 위해 해당 연구의 연구 결과에서 LSTM은 장기간의 규칙적인 시계열 학습에 높은 정확도를 보여준다는 점과 MLP는 단기간의 비규칙적인 변동성 학습에 높은 정확도를 보여주는 점에 착안하여 MLP-LSTM을 융합한 hybrid 모델을 통한 시계열 예측으로 예측 성능을 향상할 수 있음을 시사했다. BDI 시계열 예측을 시도한 선행연구들의 경우 역시, 본 연구와 같은 ANN 모델을 사용한 연구이더라도 시계열 기간의 범위, 학습 데이터의 종류, 최적화 방법, 등에 따라 다양한 연구 결괏값을 보여주고 있다. 따라서 Ouyang et al. (2021), Oh et al. (2020), 등의 선행연구들에서 주장한 바와 같이 LSTM에 대해서 hyperparameter 최적화 방법론, hybrid, ensemble 모델 등의 적용을 통해 ANN 모델이 가지는 본질적인 한계점을 극복함과 동시에 모델의 성능 향상을 기대할 수 있다.
5. 결 론본 연구에서는 선행연구와 차별화된 점으로 COVID-19 이후 불확실성이 높아진 글로벌 경제 상황에서 한정적인 데이터의 양만으로 ANN을 활용해 BDI 시계열 예측을 시도했다. ANN 알고리즘의 특성상 패턴 탐색과 예측 등의 문제해결에서 일정 수준 이상의 모델 성능 보장을 위해선 보다 대량의 데이터를 통한 학습이 필수이다. 한정된 데이터만이 주어진 상황을 극복하고 ANN의 학습 능력과 예측 정확도 향상을 위해 데이터 전처리 기법으로써 시계열 분해 및 데이터 증강 기법을 적용하여 가용 가능 데이터의 양을 극대화했다. 해당 기법을 통해 전처리된 시계열을 통해 ANN 모델들의 학습 및 예측을 진행한 경우와 해당 기법을 적용하지 않은 경우를 비교·분석했다. 해당 기법을 적용함으로써 BDI 원본 시계열만을 사용한 단변량 예측보다 개선된 예측 결과를 보여줄 것을 기대했다. 연구 결과 데이터 시계열 분해 및 데이터 증강 기법을 적용한 다변량 예측의 정확도가 해당 기법을 적용하지 않은 단변량 예측보다 높은 정확도를 보여줬다. RMSE 지표를 제외한 모든 지표에서 단변량 예측과 다변량 예측 모두 MLP가 가장 우수한 성능을 보여주는 것으로 나타났고, 차순위론 LSTM, 마지막으론 RNN이 가장 낮은 예측 정확도를 보여주고 있다. LSTM의 경우 예측 정확도의 수치는 1순위로 나타난 MLP보단 낮으나 가장 높은 지표 평균 향상률(5.656%)을 보여주고 있다. 또한, MLP와 달리 모든 성능지표에서 다변량 예측이 단변량 예측보다 우수하게 나타났다. 이에 따라 정밀한 hyperparmeter의 조정과 추가적인 데이터 투입에 따라 예측 성능 향상을 기대할 수 있는 만큼, 학습 알고리즘과 ANN 최적화 기법 등의 적용을 다양하게 시도해볼 필요가 있다. 결과적으로 본 연구를 통해 BDI 시계열을 예측한 결과 모든 ANN 모델에 대해서 단변량 예측 대비 시계열 분해 및 데이터 증강 기법을 적용한 다변량 예측의 3개 지표 평균 향상률은 1.422%(MLP: (-) 0.442%, RNN: (-) 0.947%, LSTM: 5.656%)로 나타났다. 따라서 한정된 시계열 데이터만이 주어진 상황에서 시계열 분해 및 데이터 증강 기법을 활용해 ANN의 예측 성능 향상을 추구하고자 한 본 연구의 의의 및 목표를 달성했다고 할 수 있다. 하지만 해당 수치는 실무에 적용하기엔 낮은 수치이다. 따라서 본 연구의 한계점을 극복하기 위해 다음 세 가지의 포인트를 중점으로 후속 연구를 제안한다.
1. hyperparameter의 fine tuning 및 ANN 최적화 알고리즘을 적용한 모델 예측 성능 향상
2. 단일 ANN 모델이 아닌, hybrid 또는 ensemble 모델의 접목
3. 단일 내생변수가 아닌 BDI에 영향을 미치는 요인과 인자를 고려한 다양한 외생변수의 접목
급변하는 비즈니스 및 경제 환경 또는 현재의 해운 시장 환경과 같이 가용 가능 데이터의 양이 절대적으로 부족한 상황에서 본 연구에서 시도한 접근법을 통해 비즈니스 리스크를 극복할 수 있을 것을 기대한다.
NOTES1) Archived: WHO Timeline – COVID-19, World Health Organization, 2022년 8월 26일 접속, www.who.int/news/item/27-04-2020-who-timeline---covid-19 2) Time Series & Graphs, Shipping Intelligence Network, 2022년 08월 26일 접속, www-clarksons-net.libproxy.kmou.ac.kr/n/#/sin/timeSeries/browse REFERENCESAbdollahi, H 2020. A novel hybrid model for forecasting crude oil price based on time series decomposition. Applied energy 267: 115035.
Allaire, JJ, and Chollet, F 2022. Package ‘keras’. R Interface to ‘Keras’.
Allaire, JJ, and Tang, Y 2022. Package ‘tensorflow’ R Interface to ‘TensorFlow’. In Benkachcha S, Benhra J, El Hassani H (eds.), 2015. Seasonal time series forecasting models based on artificial neural network. International Journal of Computer Applications. 116(20).
Cleveland, R. B., Cleveland, W. S., McRae, J. E., and Terpenning, I 1990. STL: A seasonal-trend decomposition. J. Off. Stat 6(1):3-73.
Demir, S., Mincev, K., Kok, K., and Paterakis, NG 2021. Data augmentation for time series regression: Applying transformations, autoencoders and adversarial networks to electricity price forecasting. Applied Energy 304: 117695.
Fritsch, S., Guenther, F., and Guenther, M. F. 2019. Package ‘neuralnet’. Training of Neural Networks.
Gers, F. A., Eck, D., and Schmidhuber, J 2002. Applyting LSTM to time series predictable through time-window approaches. In Neural Nets WIRN Vietri-01. pp 193-200. Springer. London.
Hafen, R 2016. Package ‘stlplus’. Ehanced Seasonal Decomposition of Time Series by Loess.
HAN, M, and Yu, S. J. 2019. Prediction of Baltic Dry Index by Applications of Long Short-Term Memory. Journal of the Korean Society for Quality Management 47(3):497-508.
Hansen, J. V., and Nelson, R. D. 2003. Forecasting and recombining time-series components by using neural networks. Journal of the Operational Research Society 54(3):307-317.
Iwana, B. K., and Uchida, S 2021. An empirical survey of data augmentation for time series classification with neural networks. Plos one 16(7):e0254841.
Kang, S., Cho, K., and Na, M 2021. Forecasting Crop Yield Using Encoder-Decoder Model with Attention. Journal of the Korean Society for Quality Management 49(4):569-579.
Khandelwal, I., Adhikari, R., and Verma, G 2015. Time series forecasting using hybrid ARIMA and ANN models based on DWT decomposition. Procedia Computer Science 48: 173-179.
Lee, S. W., and Kim, HY 2020. Stock market forecasting with super-high dimensional time-series data using ConvLSTM, trend sampling, and specialized data augmentation. Expert Systems with Applications 161: 113704.
Lin, Y., Koprinska, I., and Rana, M 2021. SSDNet: State space decomposition neural network for time series forecasting. In 2021 IEEE International Conference on Data Mining (ICDM). pp 370-378. IEEE.
Méndez-Jiménez, I., and Cárdenas-Montes, M 2018. Time series decomposition for improving the forecasting performance of convolutional neural networks. In Conference of the Spanish Association for Artificial Intelligence. pp 87-97. Springer. Cham.
Oh, C., Han, S, and Jeong, J 2020. Time-series data augmentation based on interpolation. Procedia Computer Science 175: 64-71.
Oliveira, D. D., Rampinelli, M., Tozatoo, G. Z., Andreao, R. V., and Muller, SM 2021. Forecasting vehicular traffic flow using MLP and LSTM. Neural Computing and applications 33(24):17245-17256.
Ouyang, Z., Ravier, P., and Jabloun, M 2021. STL Decomposition of Time Series Can Benefit Forecasting Done by Statistical Methods but Not by. Machine Learning Ones. Engineering Proceedings 5(1):42.
Quast, B, and Fichou, D 2022. Package ‘rnn’. Recurrent Nerual Network.
Figure 6.Data Augmentation by Jittering (Gaussian distribution α ∼ N(1, σ2), where μ = 0, σ = 0.03) 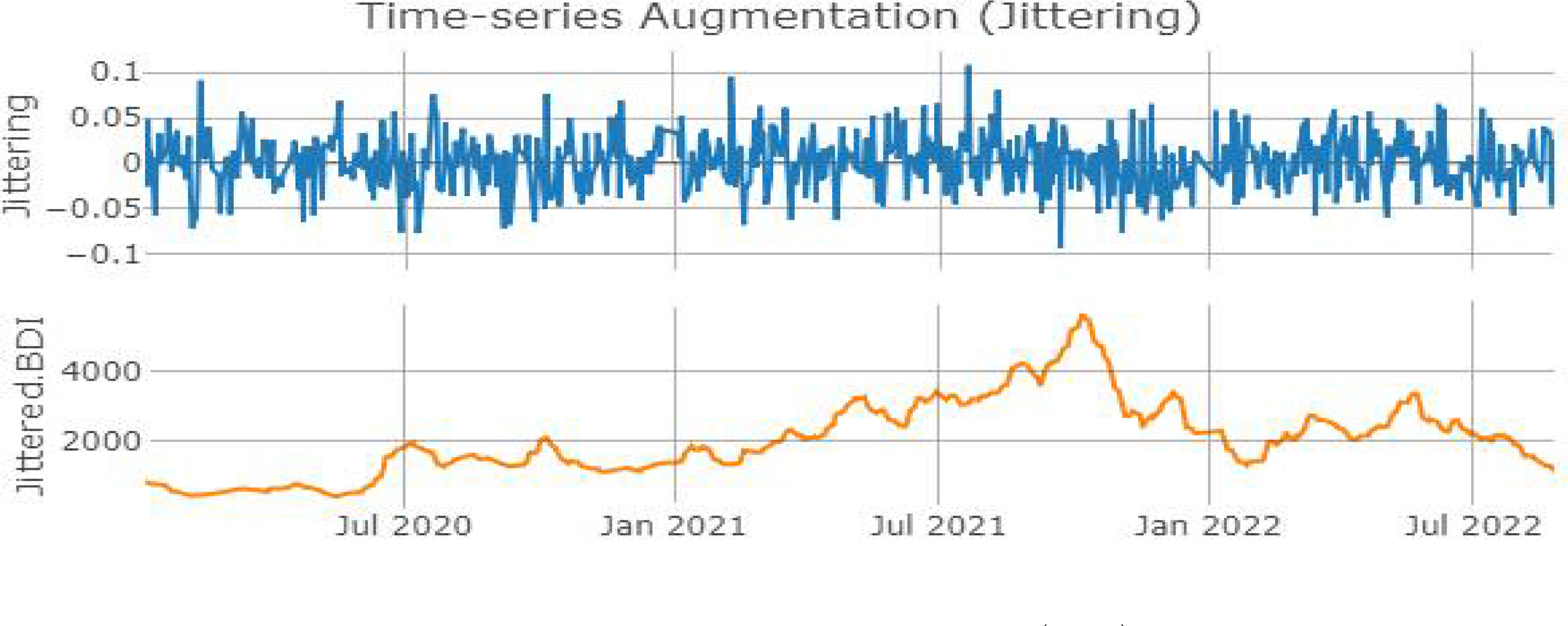
Figure 7.One Day-Ahead Forecasting by Multi-Layer Perceptron (MLP) [Univariate MLP Vs. Multivariate MLP] 
Figure 8.One Day-Ahead Forecasting by Recurrent Neural Network (RNN) [Univariate RNN Vs. Multivariate RNN] 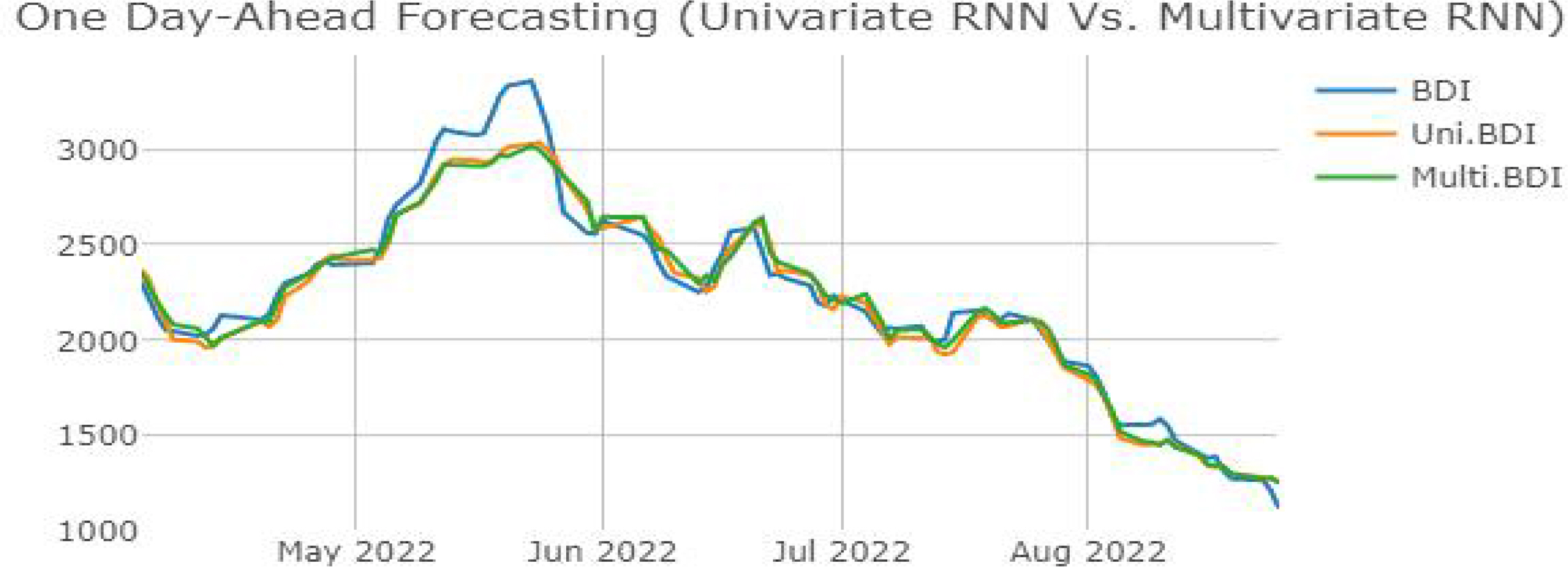
Figure 9.One Day-Ahead Forecasting by Long Short-Term Memory (LSTM) [Univariate LSTM Vs. Multivariate LSTM] 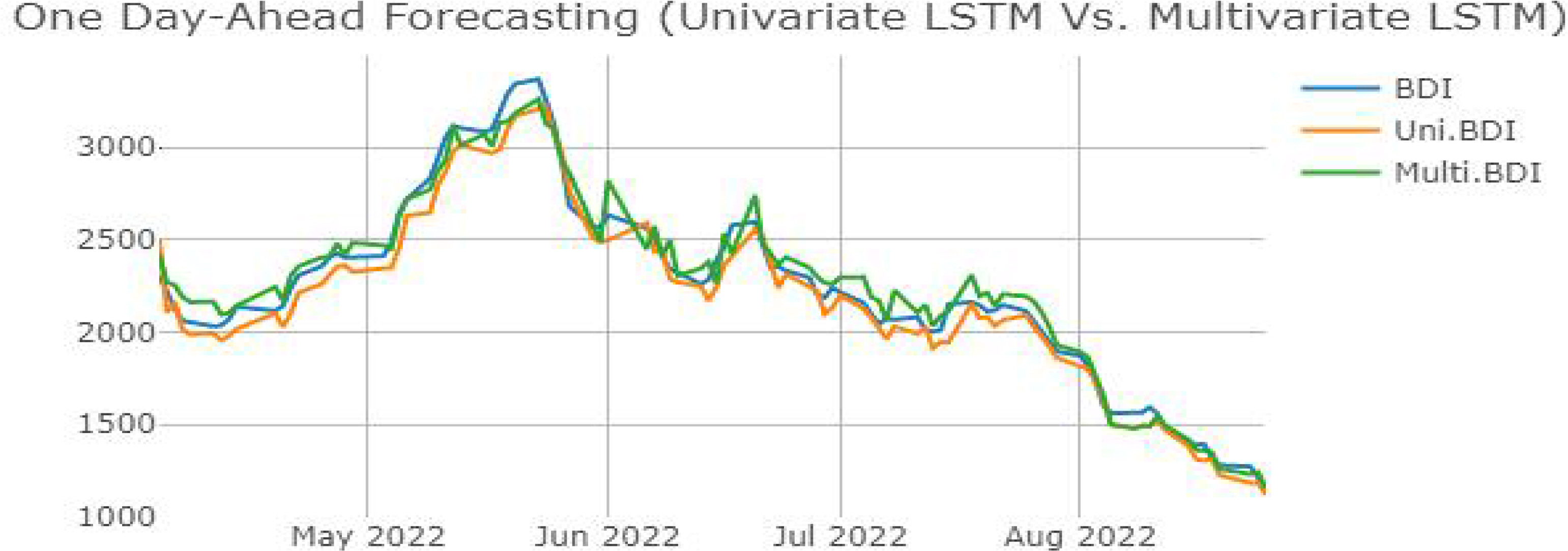
Table 2.Advantages and Disadvantages of Seasonal and Trend Decomposition Using Losses
Table 3.Result of the Artificial Neural Network Prediction Accuracy Table 4.Result of the Artificial Neural Network Prediction Accuracy |
|
||||||||||||||||||||||||||||||||||||