신뢰성 분석 기반 발전설비 점검계획 수립 시스템 연구 - 석탄 하역기를 중심으로 -
Abstract
Purpose
Recently, research has continued to predict the time of failure of the facility through measurement data obtained by attaching a sensor to the facility. However, depending on the facility, it may be difficult to attach a sensor. The purpose of this study is to propose a power generation maintenance plan system based on failure record data obtained from Continuous Ship Unloader, one of the facilities that is difficult to attach sensors.
Methods
This study uses data collected from 2012 to 2022 from the ‘CSU-1B’ model among Continuous Ship Unloader operated by Korea Midland Power Co., LTD. By fitting fault record data to the Weibull distribution, appropriate maintenance cycles and ranges for each target facility subsystem are derived. In addition, maintenance group between subsystems is selected through Euclidean distance, a metric often used for time series data similarity. Through this, a system for establishing an maintenance plan for power generation facilities is proposed.
Results
The results of this study are as follows. For the 17 subsystems of the Continuous Ship Unloader, proper maintenance cycles and ranges were determined, and a total of four maintenance groups were chosen. This resulted in the creation of an power generation maintenance plan system and the establishment of an maintenance plan.
Conclusion
This study is a case study of power generation facilities. We proposed a maintenance plan system for Continuous Ship Unloader among power generation facilities.
Key words: Power Generation Facilities, Preventive Maintenance, Reliability Analysis, Maintenance Scheduling, Continuous Ship Unloader
1. 서 론
본 연구의 대상 장비인 석탄 하역기는 화력발전소의 연료인 석탄을 선박으로부터 육지로 운송하기 위해 사용되는 장비로, 고정되어 있는 기기가 아닌 기체 자체가 움직이는 이동기이므로 센서 부착이 제한적이다. 따라서, 본 연구에서는 대상 장비의 하위 시스템 고장 기록 데이터를 수집하여 신뢰성 분석을 통해 핵심 지표를 산출하고, 이를 기반으로 적정 점검 주기 및 범위를 선정한다. 또한 고장 발생 상관도를 도출하여 동시에 고장이 날 확률이 높은 하위 시스템끼리 그룹핑한다. 적정 점검 주기 및 범위 산출과 점검 그룹 선정 과정을 통합하여, 그룹 내 하위 시스템이 동시에 점검을 진행할 구간을 선정하고 다음 점검 시기를 산정하는 발전설비 점검계획 수립 시스템을 제안하고자 한다.
2. 이론적 배경 및 선행연구
2.1 신뢰성 분석
신뢰성 분석은 제품, 시스템 또는 프로세스가 주어진 조건 하에서 예상 수명 동안 특정 기능을 수행하는 능력을 정량화하고 예측하는데 사용된다( Han et al., 2021). 이는 고장률, 수명과 같은 신뢰성 지표를 통해 예상 수명과 기능성을 예측하며, 제품 또는 시스템의 개선과 유지보수 계획에 중요한 역할을 한다. 신뢰성 분석에서 보편적으로 활용되는 수명분포 모형은 와이블 분포, 대수정규 분포, 지수 분포 등이 있다. 이 중 와이블 분포는 형태가 다른 분포에 비해 유연하여 다양한 형태의 신뢰성 데이터를 잘 표현할 수 있다. 와이블 분포는 형상 모수(β)와 척도 모수(η) 2개의 모수를 가지며 모수를 조정함으로써 고장률이 시간에 따라 증가, 감소, 유지되는 다양한 실제 상황을 반영할 수 있어 설비의 신뢰성 분석에 주로 적용된다( Kim et al., 2022). 발전설비 중 회전기기의 정비 이력 데이터를 통해 신뢰도 중심정비 방법론을 사용하여 최적의 정비 주기를 도출하는 연구를 진행하였다( Kim et al., 2021). 해당 연구는 펌프, 팬, 모터를 대상 설비로 하여 신뢰성 분석을 통해 핵심 지표를 도출하여 의사결정 알고리즘에 적용하여 최적의 정비 주기를 도출하였다. 해당 연구는 최적의 정비 주기만을 도출하여 특정 시기에 정비를 위해 설비를 정지하기 어려운 발전설비 특성을 고려하지 못하는 한계점을 가진다. 본 연구는 대상 설비의 고장 기록 데이터를 통해 신뢰성 분석을 진행하여 신뢰성 지표인 평균고장시간(MTTF : Mean Time To Failure)과 백분위 수명(B 수명)을 도출한다. 이를 통해, 적정 점검 주기 및 범위를 도출하여 특정 시기가 아닌 점검 범위 내 점검 시기를 해당 설비에 맞게 유연하게 정할 수 있다.
2.2 시계열 분포 유사도 측정
일반적인 유사도 측정은 주로 데이터의 형태나 분포를 비교하는데 초점을 맞춘다. 반면 시계열 분포의 유사도는 시간 순서에 따른 데이터의 변화를 중요하게 보며, 순서가 결과에 영향을 미친다. 또한, 데이터의 시간적인 패턴과 추세를 비교하는 것이 중요하다. 시계열 데이터의 유사도를 측정하는 방법은 주로 유클리드 거리, 동적 시간 워핑(DTW : Dynamic Time Wrapping)이 사용된다. 유클리드 거리는 두 시계열 데이터 간의 직선 거리를 측정하는 방법으로 두 데이터가 정확히 같은 시간에 일어나야 유사도가 높게 측정된다. 동적 시간 워핑은 두 시계열 데이터가 시간 축에서 약간의 차이가 있더라도 그 유사도를 측정할 수 있게 해주는 방법이다( Choi and Cho, 2021). 본 연구에서는 시계열 데이터인 대상 설비의 각 하위 시스템별 고장 발생 이력 데이터를 통해 유사도를 측정하여 동시에 점검을 진행하는 점검 그룹을 선정한다. 각 하위 시스템별 고장 발생 이력 데이터는 시간 범위가 일정하기 때문에 계산 비용이 높은 동적 시간 워핑이 아닌 각 시간 단계에서 값의 차이를 단순히 계산하여 계산 속도가 빠른 유클리드 거리를 사용하였다.
2.3 점검계획
점검계획은 고장이나 결함이 발생하기 전에 미리 발견할 수 있도록 하여 장비의 수명을 연장하는 데 도움이 된다. 장비의 고장을 미리 예방함으로써 긴급 수리 및 교체에 드는 비용을 절감할 수 있다. 또한, 장비의 결함을 최소화하여 장비 작동 중단을 줄여 생산 효율을 높일 수 있다. 이와 같은 이유로 점검계획은 설비를 운영하는 데 있어 필수적이다.
전력망을 효율적으로 유지 보수하기 위해 수리계획-발견적 복합 알고리즘을 사용하여 점검계획을 수립하는 연구를 진행하였다( Joo et al., 2022). 일정 기간동안 진행되는 전력망 각 구성 요소들의 작업 수행 시기를 결정하는 추계적 작업 할당 문제를 풀기 위해 알고리즘을 제시하였다. 해당 연구를 완벽히 적용하기 위해서는 수행해야 할 작업 데이터, 각 작업의 불확실성을 측정하기 위한 확률적 데이터 등 추가적인 데이터의 활용이 필수적이라는 한계가 존재한다. 이에 본 연구는 각 발전설비의 고장 이력 데이터만을 사용하여 보다 범용적인 발전설비의 점검계획 시스템을 제안한다.
3. 대상 설비 및 데이터
3.1 대상 설비
본 연구는 한국중부발전에서 운영 중인 연속식 석탄 하역기(CSU : Continuous Ship Unloader)중 CSU-1B 호기를 분석 대상 장비로 선정한다. CSU-1B 호기의 구성은 [ Figure 1]과 같다. 석탄 하역기는 135,000 DWT 크기의 대양 횡단 선박에서 0.8 t/m2 비중인 발전소용 석탄을 하역하기 위한 장비이다. 분석 대상 장비인 석탄 하역기 CSU-1B는 < Table 1>과 같이 17개의 하위 시스템으로 구성되어 있다. CSU-1B는 석탄 하역 설비가 포함된 상부 구조물과 이동을 위한 동력 설비가 있는 하부 구조물 두 부분으로 구성되어 있다. 상부 구조물은 선박의 화물칸에서 하역할 석탄을 버켓 엘리베이터(B/E : Bucket/Elevator)를 이용해 붐 컨베이어(BOOM CONVEYOR)로 전달한다. 이후, 붐 컨베이어를 통해 이동한 석탄을 하부 구조물로 보낸다. 하부 구조물은 석탄 하역기의 이동을 담당하는 하역기 이동부(GANTRY TRAVEL)와 상부 구조물에서 내려온 석탄을 저탄장으로 전달하는 하역기 컨베이어(GANTRY CONVEYOR)로 이루어져 있다. CSU-1B의 핵심 구동 설비는 유압 구동 방식을 사용하며, 이를 HPP 시스템(HPP SYS)이라고 일컫는다.
3.2 분석 데이터
분석에 사용된 데이터는 < Table 2>와 같이 2012년 7월부터 2022년 4월까지의 17개 하위 시스템에 대한 고장 기록 데이터로 구성되어 있다. 석탄 하역기에서 발생한 총 1,161건의 고장 중에서 상부 구조물에서는 643건, 하부 구조물에서는 267건, 그리고 유압 시스템에서는 251건의 고장이 발생했다. 이 연구의 목적은 해당 데이터를 분석하여 적정 점검 주기와 범위를 도출하고, 점검 그룹을 선정하여 발전설비 점검계획을 수립하는 것이다.
4. 발전설비 점검계획 시스템
본 연구에서는 4.1절과 4.2절을 통해 대상 장비의 하위 시스템별로 도출된 적정 점검 주기와 점검 그룹을 통해 [ Figure 2]와 같이 발전설비 점검계획 시스템을 제안한다.
4.1 적정 점검 주기 및 범위 도출
분석 대상인 장비의 하위 시스템별 고장 기록 데이터를 이용하여 각 시스템의 적절한 점검 주기와 범위를 도출한다. 적정 점검 주기 및 범위를 도출하는 과정은, 고장 기록 데이터를 와이블 확률지에 타점한 후, 추정된 와이블 분포의 모수를 통해 MTTF와 B 수명을 계산하는 순서로 진행된다( Kim and Kim, 2020). 본 연구에서 와이블 분포의 모수를 추정하기 위한 방법론으로는 최우 추정법을 채택한다( Kim, 2018). 분석 대상 장비의 하위 시스템 중 하나인 ‘B/E BUCKET & CHAIN DEVICE’의 와이블 확률지 표시 결과는 [ Figure 3]과 같다. 추정된 형상 모수(β)와 척도 모수(η)는 확률지 타점에 의해 신뢰구간을 가지게 되고, ‘B/E BUCKET & CHAIN DEVICE’의 와이블 분포 모수 추정 결과는 < Table 3>과 같다. 도출한 형상 모수와 척도 모수의 점 추정치, 신뢰구간 하한치, 신뢰구간 상한치를 이용하여 누적 와이블 분포를 산정하여 각 수치마다 신뢰성 지표인 평균 고장 시간(MTTF)과 백분위 수명을 나타내는 B 수명을 < Table 4>와 같이 산출한다. 이후, < Table 5>(Algorithm 1)에 해당 값을 통해 대상 설비 하위 시스템별 적정 점검 주기 및 범위를 도출한다. ‘B/E BUCKET & CHAIN DEVICE’의 모수 점 추정치로부터 얻어진 B 수명 중 MTTF 60일보다 작지만 가장 근접한 값인 B60 수명(53일)을 적정 점검 주기로 선택한다. 대상 장비의 특성상, 석탄 하역기의 점검계획을 세울 때 특정 시기에 점검을 실행하기 어렵다. 따라서, 본 연구에서는 추정된 와이블 분포 모수의 신뢰구간 하한값와 상한값을 사용하여 적정 점검 범위를 계산한다.
B60 수명, 즉 모수의 점 추정치에서 선정된 B 수명을 신뢰구간 하한값과 상한값에 대입하여 < Table 4>에 따라 최소 점검 시기를 38일로, 최대 점검 시기를 73일로 결정한다. 추출된 값에 따라 ‘B/E BUCKET & CHAIN DEVICE’의 하한 점검 범위는 기준인 53일로부터 -15일이며, 상한 점검 범위는 53일로부터 +20일이다. 위와 같은 절차를 거쳐 추출된 17개 대상 설비 하위 시스템별 적절한 점검 주기와 범위는 < Table 6>과 같다.
4.2 점검 그룹 선정
대상 장비의 하위 시스템 중, 동시에 고장이 날 확률이 높은 시스템끼리 그룹핑하여 점검 그룹을 선정한다. 점검 그룹 선정 과정은 고장 기록 데이터를 통해 시계열 고장 발생 이력 데이터를 생성하여 각 하위 시스템별 시계열 분포의 유사도를 유클리드 거리를 통해 측정한다. 측정된 유사도를 통해 동시에 고장이 날 확률이 높은 시스템을 점검 그룹으로 선정한다.
첫째로, 고장 발생 이력 데이터를 생성한다. 해당 데이터는 시간 순서대로 각 하위 시스템별 작동 시간과 비작동 시간 산정한 데이터로 < Table 7>과 같이 고장이 난 상태일 경우 1, 정상인 상태는 0의 값을 가지는 시계열 데이터이다. 본 연구에서는 생성된 고장 발생 이력 데이터로 하위 시스템 간의 고장 발생 상관도를 도출하기 위해 시계열 분포 유사도 측정에 많이 사용되는 유클리드 거리를 계산한다( Loh et al., 2006). 유클리드 거리는 값이 0 이상이며 0에 가까울수록 두 데이터가 유사하다는 것을 의미한다( Kim et al., 2014). [ Figure 4]는 생성한 17개의 하위 시스템별 고장 발생 이력 데이터를 통해 측정한 하위 시스템 간의 유클리드 거리이다. 도출된 고장 발생 상관도의 Q1값인 29.81을 임계값으로 설정하여 점검 그룹을 선정한다. ‘B/E BUCKET & CHAIN DEVICE’의 경우 고장 발생 상관도 값이 임계값 보다 작은 27.75 값을 가지는 ‘BOOM SLEW STRUCTURE’를 점검 그룹으로 선정한다. 상기와 같은 과정을 거쳐 17개의 대상 장비 하위 시스템에서 선정된 점검 그룹은 < Table 8>과 같다.
4.3 발전설비 점검계획 시스템
본 연구에서 제안하는 발전설비 점검계획 시스템은 4.1절의 적정 점검 주기 및 범위와 4.2절의 점검 그룹을 통합하여 점검계획을 수립한다. 점검 그룹 내 하위 시스템의 적정 점검 주기 및 범위를 사용하여 < Table 10>(Algorithm 2)을 통해 발전설비 하위 시스템의 동시에 점검을 진행할 점검 구간 선정 및 다음 점검 시기를 산정하여 점검계획을 수립한다. ‘B/E BUCKET & CHAIN DEVICE’과 점검 그룹으로 선정된 하위 시스템은 ‘BOOM SLEW STRUCTURE’이다. 해당 2개의 시스템에서 도출된 적정 점검 주기 및 점검 범위는 < Table 9>와 같다. 해당 점검 그룹의 하위 시스템 중 적정 점검 주기가 가장 작은 값을 가지는 ‘BOOM SLEW STRUCTURE’를 해당 점검 그룹의 기준 시스템으로 선정한다. 기준 시스템의 점검 범위가 점검 그룹 내 다른 하위 시스템의 점검 범위와 겹치는 구간이 있는지 확인하며 동시에 점검을 진행할 점검 구간을 선정한다. 기준 시스템의 점검 범위와 겹치는 하위 시스템과 기준 시스템은 동시 점검 구간의 중위수를 기준으로 각 시스템의 적정 점검 주기를 더하여 다음 점검 시기를 산정한다. 기준 시스템의 점검 범위와 겹치지 않는 하위 시스템은 기존 점검 주기를 그대로 유지한다. 동시 점검 구간과 다음 점검 시기를 산정하며 점검계획 수립 시 지정한 기간 범위만큼 상기 과정을 반복한다. 점검 그룹 Group A의 점검계획 수립 기간을 200일로 지정하였을 때 본 연구에서 제안하는 발전설비 점검계획 시스템을 통해 도출된 점검계획은 [ Figure 5]와 같다.
5. 결 론
본 연구는 발전설비 중 석탄 하역기의 고장 기록 데이터를 바탕으로 적정 점검 주기 및 범위 산출과 점검 그룹 선정을 진행하고, 이를 통합하여 효율적으로 고장 예방에 기여할 수 있는 발전설비 점검계획 수립 시스템을 제안한다. 대상 설비 하위 시스템의 고장 기록 데이터를 신뢰성 분석하여 와이블 분포의 형상 모수(β)와 척도 모수(η)를 추정한다. 추정된 모수의 점 추정치 및 신뢰구간을 이용하여 MTTF와 B 수명을 산출한다. MTTF보다 작지만 가장 근접한 값을 갖는 B 수명을 적정 점검 주기로 선택하고, 추정된 모수의 신뢰구간을 사용하여 적정 점검 범위를 산출한다. 또한, 고장 기록 데이터를 통해 시계열 고장 발생 이력 데이터를 생성한다. 생성한 값을 토대로 유클리드 거리를 활용하여 각 하위 시스템별 시계열 분포의 유사도를 측정한 후 동시에 고장이 날 확률이 높은 하위 시스템끼리 점검 그룹으로 그룹핑한다. 도출된 적정 점검 주기 및 범위와 점검 그룹을 통해 같은 시기에 고장이 날 확률이 높은 하위 시스템끼리 동시에 점검을 진행할 수 있도록 동시 점검 구간을 선정하고, 이를 바탕으로 다음 점검 시기를 산정하여 점검계획을 수립하였다.
기존 발전소 중 일부는 설비 점검 방식으로 사후보전을 채택하고 있으나, 발전설비 특성상 사후보전을 실시할 경우 발생하는 손실이 상당히 크다는 문제가 있다. 본 연구에서 제안한 발전설비 점검계획 시스템을 적용할 경우, 사후보전으로 인한 돌발 정비 실행 시 발생하는 손실을 줄일 수 있다. 또한 고장을 사전에 예방할 수 있도록 기여하여 설비의 안정성 및 신뢰성을 향상시킬 수 있으며, 점검 작업의 효율성을 높일 수 있을 것으로 보인다. 또한 적정 점검 주기 뿐만 아니라 점검 범위를 제시하여, 의사 결정자들이 상황에 따라 유연하게 최적의 점검 전략을 수립할 수 있다. 본 연구는 발전설비 중 하나인 석탄 하역기를 대상으로 분석을 진행하여 발전설비 내 전체 시스템을 고려하지 않았다는 한계가 있다. 따라서 향후 미분기, 보일러 튜브와 같은 발전설비를 추가로 분석하여 통합 발전설비 점검계획 시스템을 구축하고자 한다.
REFERENCES
Chae, C., and Kwon, Y. 2017. Sensorless maximum power control of wind power synchronous generator with compensated parameter. Journal of Advanced Marine Engineering and Technology 41(9):902-907.  Choi, W., and Cho, J. 2021. Design and Implementation of High-speed DTW Accelerator for Time-series Data Classification. Journal of the Institute of Electronics and Information Engineers 58(3):51-58.  Han, S, Yun, Y, and Seo, S. 2021. Economic Design of A Zero-Failure Reliability Demonstration Test Considering Capacity Limitation of Test Equipment. Journal of the Korean Society for Quality Management 49(3):341-358.
Hong, S., and Jung, S. 2016. A Study of Reliability of Guided Missile(OO) using Probit Analysis. Journal of the Korean Society for Quality Management 44(3):553-564.  Joo, J, Roh, Y, Park, H, Lee, J, and Lee, C 2022. A Hybrid Mathematical Programming-Heuristic Algorithm for a Sustainable Power Grid Maintenance Scheduling. Journal of the Korean Institute of Industrial Engineers 48(1):13-34.  Jung, S., and Kim, S. 2021. Fault Detection Method for Multivariate Process using Mahalanobis Distance and ICA. Journal of Korea Institute of Information, Electronics, and Communication Technology 14(1):22-28.
Kim, Y, Kim, C, and Jeong, K 2022. Analysis of Replacement Cycle based on Inspection Statistics of Receiving Power Transformer for Private Electrical Facilities. Transactions of The Korean Institute of Electrical Engineers 71(1):275-281.  Kim, H. 2018. A Study on Attribute Analysis of Software Development Cost Model about Life Distribution Considering Shape Parameter of Weibull Distribution. Journal of Korea Institute of Information, Electronics, and Communication Technology 11(6):645-650.
Kim, H., No, Y., Son, J., Im, K., and Kim, S. 2021. A Study on the Hybrid Reliability Centered Maintenance Methodology for Rotating Machinery in Power Plants. Transactions of the KSME C Industrial Technology and Innovation 9(1):75-83.  Kim, K., Kim, D., and Lee, J. 2014. Measuring Similarity Between Movies Based on Polarity of Tweets. Journal of Korean Institute of Intelligent Systems 24(3):292-297.  Kim, M., and Kim, M. 2020. Development of a Reliability Dashboard for Analyzing Warranty Data of Vacuum Pumps for Semiconductor Processes. Journal of Applied Reliability 20(3):225-234.  Kim, M., and Park, M. 2019. Determining an Optimal Production Time for EPQ Model with Preventive Maintenance and Defective Rate. Journal of the Korean Society for Quality Management 47(1):87-96.
Lee, H, Hong, Y, and Kang, S 2021. Identifying Process Capability Index for Electricity Distribution System through Thermal Image Analysis. Journal of the Korean Society for Quality Management 49(3):327-340.
Lee, S., and Kim, Y. 2022. A Pre-processing Process Using TadGAN-based Time-series Anomaly Detection. Journal of the Korean Society for Quality Management 50(3):51-58.
Loh, W., Moon, Y., and Kim, Y. 2006. An Efficient Algorithm for Streaming Time-Series Matching that Supports Normalization Transform. Journal of KISS: Databases 33(6):600-619.
Sang, M., Lee, N., Shin, Y., Lee, C., and Oh, Y. 2021. An Optimization Model for O&M Planning of Floating Offshore Wind Farm using Mixed Integer Linear Programming. Journal of the Korea Society of Computer and Information 26(12):255-264.
Tenbohlen, S., Vahidi, F., Gebauer, J., Krüger, M., and Müller, P 2011. Assessment of Power Transformer Reliability. XVII International Symposium on High Voltage Engineering. 22-26.
Yssaad, B., Khiat, M., and Chaker, A. 2014. Reliability centered maintenance optimization for power distribution systems. International Journal of Electrical Power & Energy Systems 55: 108-115. 
Figure 1.
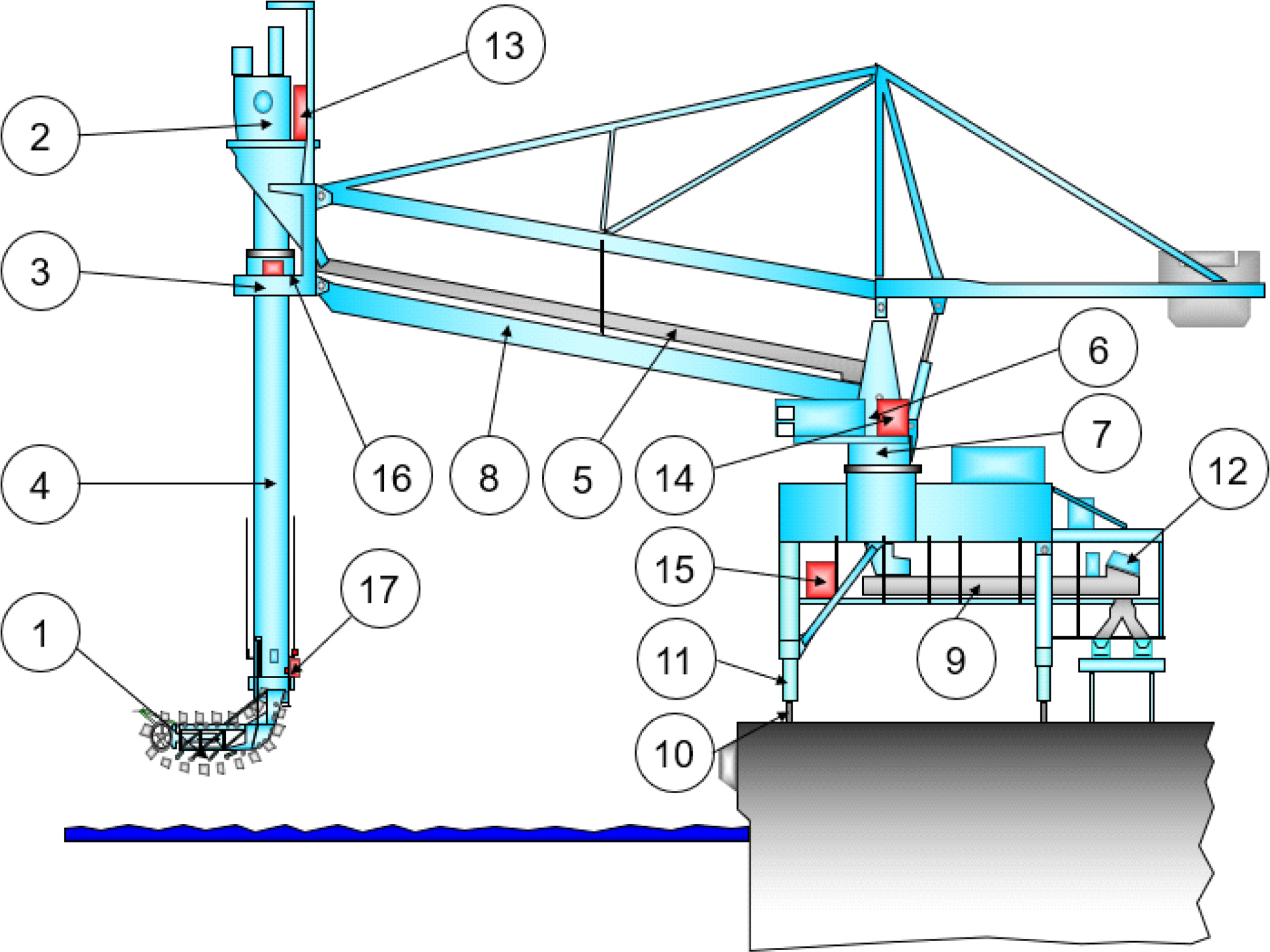
Figure 2.
Flow Chart for Maintenance Plan System 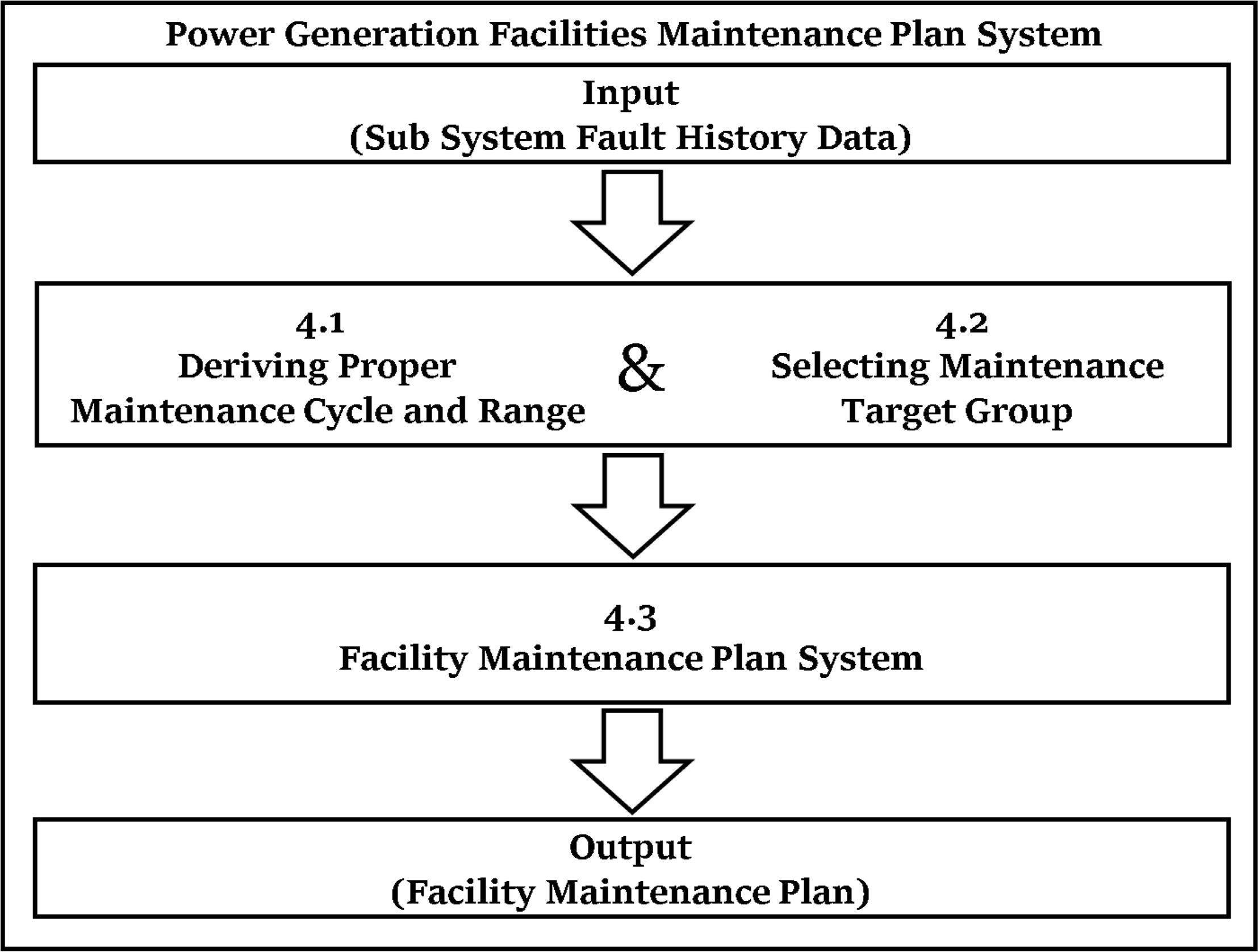
Figure 3.
B/E BUCKET & CHAIN DEVICE Weibull Probablity Plot Result 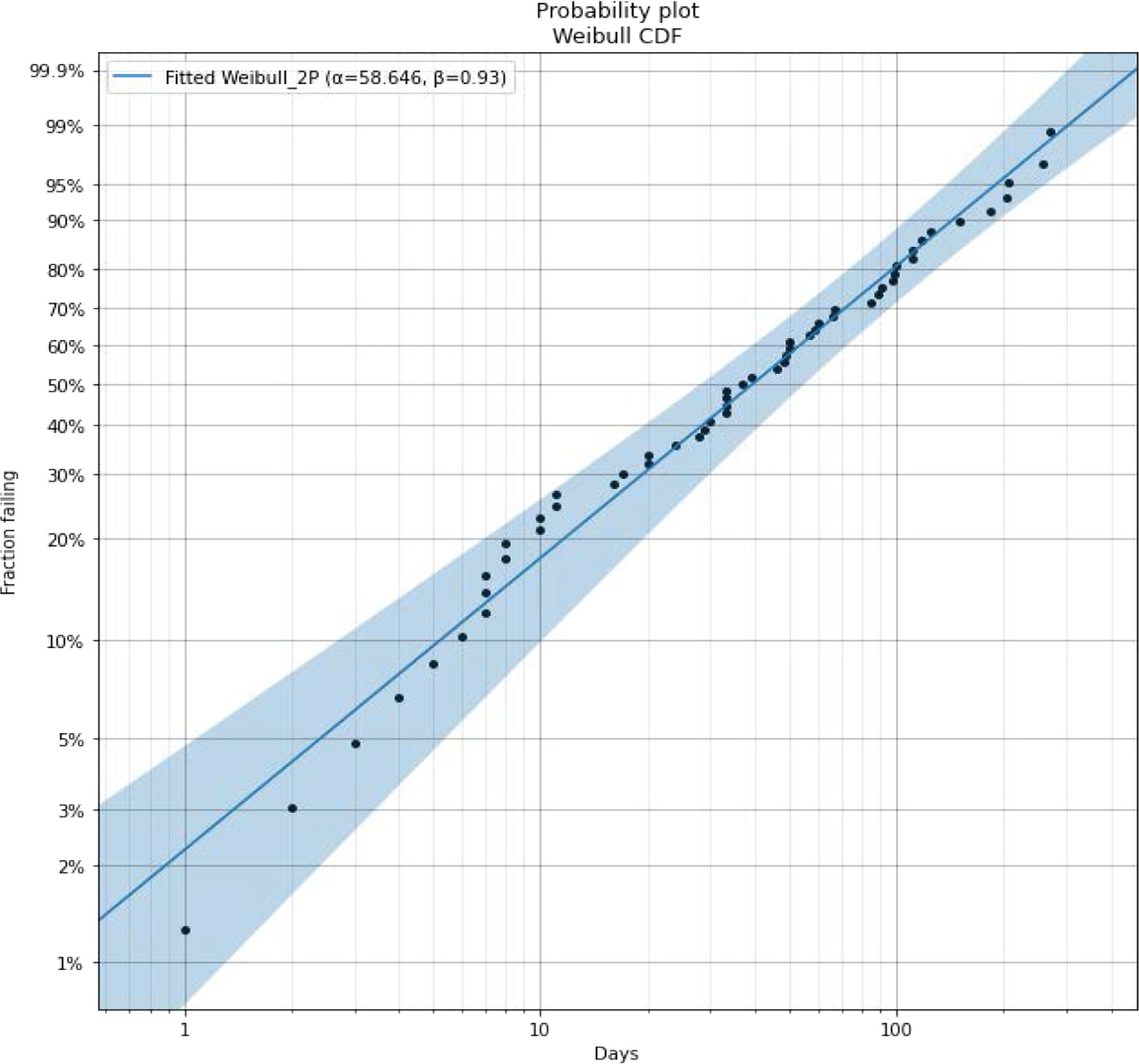
Figure 4.
Euclidean Distance Metric between Sub systems 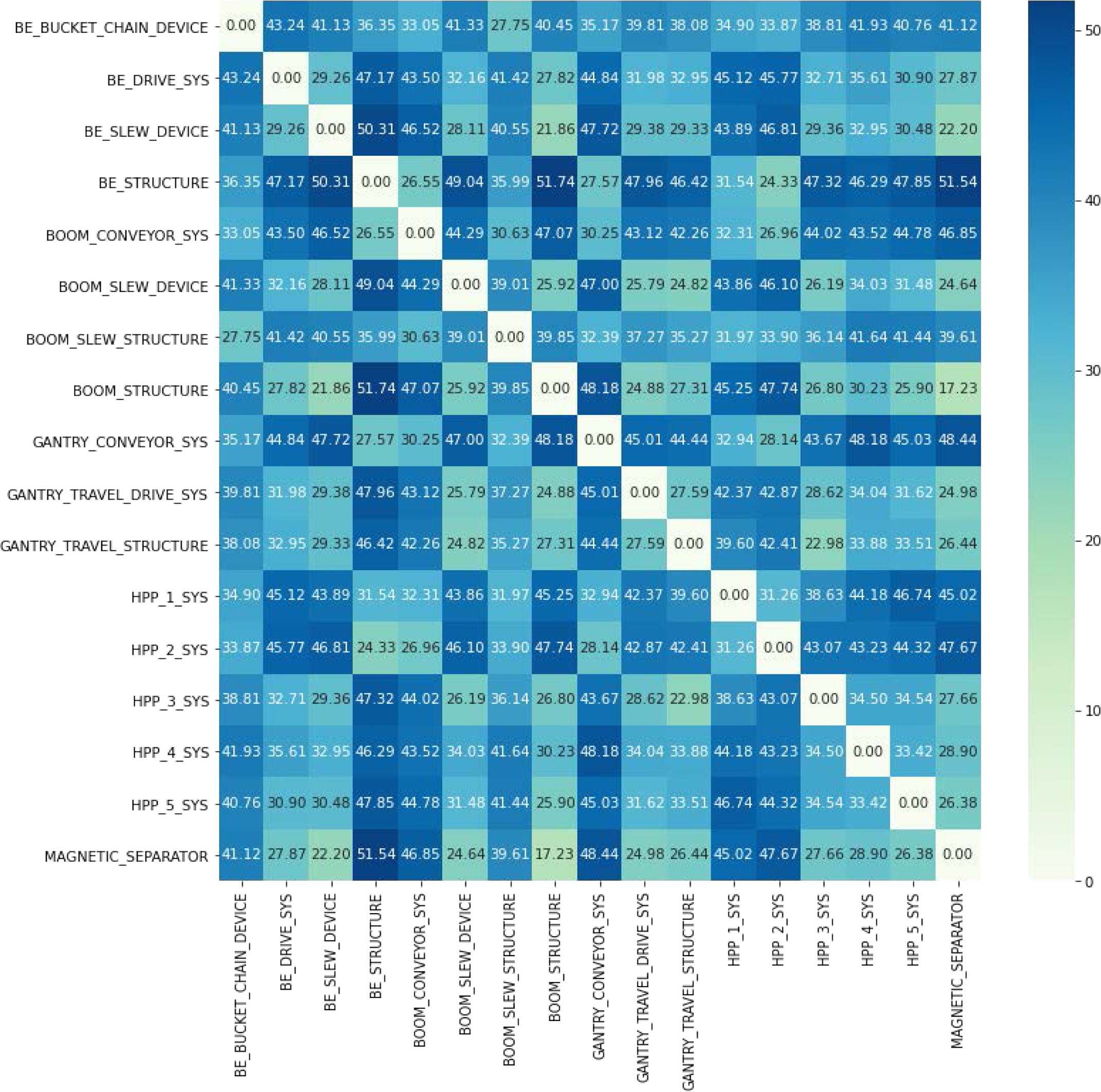
Figure 5.
Maintenance Group A Maintenance Plan 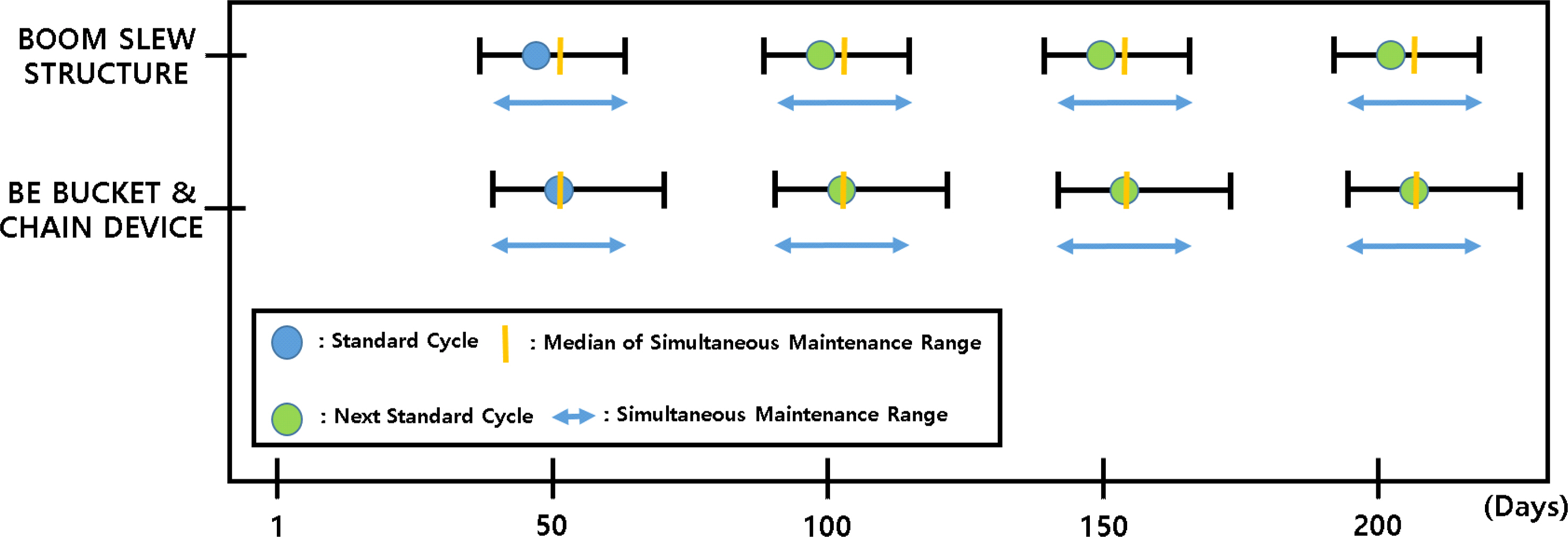
Table 1.
Target Facility Sub Systems
|
Sub system
|
Sub System
|
|
1 |
B/E BUCKET & CHAIN DEVICE |
10 |
GANTRY TRAVEL DRIVE SYS |
|
2 |
B/E DRIVE SYS |
11 |
GANTRY TRAVEL STRUCTURE |
|
3 |
B/E SLEW DEVICE |
12 |
MAGNETIC SEPARATOR |
|
4 |
B/E STRUCTURE |
13 |
HPP 1 SYS |
|
5 |
BOOM CONVEYOR SYS |
14 |
HPP 2 SYS |
|
6 |
BOOM SLEW STRUCTURE |
15 |
HPP 3 SYS |
|
7 |
BOOM SLEW DEVICE |
16 |
HPP 4 SYS |
|
8 |
BOOM STRUCTURE |
17 |
HPP 5 SYS |
|
9 |
GANTRY CONVEYOR SYS |
|
|
Table 2.
Target Facility Sub Systems Fault Data
|
Structure
|
Sub system
|
Fault Count
|
Structure
|
Sub system
|
Fault count
|
|
Super Structure |
B/E BUCKET & CHAIN DEVICE |
58 |
Sub Structure |
GANTRY TRAVEL DRIVE SYS |
47 |
|
B/E DRIVE SYS |
33 |
GANTRY TRAVEL STRUCTURE |
16 |
|
B/E SLEW DEVICE |
13 |
|
MAGNETIC SEPARATOR |
10 |
|
B/E STRUCTURE |
276 |
|
HPP 1 SYS |
108 |
|
BOOM CONVEYOR SYS |
154 |
|
HPP SYS |
HPP 2 SYS |
65 |
|
BOOM SLEW STRUCTURE |
67 |
|
HPP 3 SYS |
28 |
|
BOOM SLEW DEVICE |
30 |
|
HPP 4 SYS |
26 |
|
BOOM STRUCTURE |
12 |
|
HPP 5 SYS |
24 |
|
Sub Structure |
GANTRY CONVEYOR SYS |
194 |
Table 3.
‘B/E BUCKET & CHAIN DEVICE’ Result of Weibull Analysis
|
Parameter
|
Beta (β) |
Eta (η) |
|
Point Estimate
|
0.9262 |
58.6464 |
|
S.E
|
0.0979 |
8.9793 |
|
Lower CI
|
0.7563 |
43.4425 |
|
Upper CI
|
1.1427 |
79.1714 |
Table 4.
‘B/E BUCKET & CHAIN DEVICE’ Reliability Scale
|
Lower CI |
Point Estimate |
Upper CI |
|
MTTF
|
51 days |
60 days |
75 days |
|
B10
|
2 days |
5 days |
11 days |
|
B20
|
5 days |
11 days |
21 days |
|
B30
|
11 days |
19 days |
32 days |
|
B40
|
17 days |
28 days |
43 days |
|
B50
|
26 days |
39 days |
57 days |
|
B60
|
38 days |
53 days |
73 days |
|
B70
|
55 days |
71 days |
93 days |
|
B80
|
81 days |
97 days |
120 days |
|
B90
|
130 days |
143 days |
164 days |
Table 5.
Deriving Proper Maintenance Cycle and Range
Algorithm 1.
Deriving Proper Maintenance Cycle and Range |
|
Input:
|
MTTF : Mean Time to Failure |
|
B-Life : Percentage Life of Facility |
|
P : Point Estimate |
|
L : Lower CI |
|
U : Upper CI |
|
|
Output:
|
CM: Proper Maintenance Cycle |
|
BU: Upper Maintenance Bound |
|
BL: Lower Maintenance Bound |
|
|
Procedure:
|
For Bx in {B-Life}P : If, {Bx}P<{MTTF}P : Return argmax {Bx}PBx
|
|
CM={Bx}P
|
|
BU={Bx}h-{Bx}P
|
|
BL={Bx}P-{Bx}l
|
Table 6.
Maintenance Cycle and Range for Target Facility Sub Systems
|
Sub System |
Standard Maintenance Cycle |
Lower Maintenance Bound |
Upper Maintenance Bound |
|
B/E BUCKET & CHAIN DEVICE |
53 days |
−15 days |
+20 days |
|
B/E DRIVE SYS |
99 days |
−30 days |
+42 days |
|
B/E SLEW DEVICE |
317 days |
−145 days |
+293 days |
|
B/E STRUCTURE |
12 days |
−2 days |
+3 days |
|
BOOM CONVEYOR SYS |
28 days |
−6 days |
+8 days |
|
BOOM SLEW STRUCTURE |
49 days |
−14 days |
+20 days |
|
BOOM SLEW DEVICE |
140 days |
−57 days |
+103 days |
|
BOOM STRUCTURE |
226 days |
−133 days |
+308 days |
|
GANTRY CONVEYOR SYS |
17 days |
−4 days |
+5 days |
|
GANTRY TRAVEL DRIVE SYS |
79 days |
−23 days |
+34 days |
|
GANTRY TRAVEL STRUCTURE |
218 days |
−102 days |
+187 days |
|
MAGNETIC SEPARATOR |
442 days |
−171 days |
+269 days |
|
HPP 1 SYS |
47 days |
−10 days |
+13 days |
|
HPP 2 SYS |
54 days |
−15 days |
+22 days |
|
HPP 3 SYS |
163 days |
−67 days |
+121 days |
|
HPP 4 SYS |
173 days |
−62 days |
+103 days |
|
HPP 5 SYS |
156 days |
−67 days |
+126 days |
Table 7.
Target Facility Fault Mode Data
|
SYS |
B/E BUCKET & CHAIN DEVICE |
B/E DRIVE SYS |
… |
HPP 4 SYS |
HPP 5 SYS |
|
Date |
|
2012/07/06 |
0 |
0 |
… |
0 |
1 |
|
2012/07/07 |
0 |
0 |
… |
0 |
1 |
|
2012/07/08 |
0 |
1 |
… |
1 |
1 |
|
… |
… |
… |
… |
… |
… |
|
2023/04/23 |
0 |
1 |
… |
0 |
0 |
|
2023/04/24 |
0 |
1 |
… |
0 |
0 |
|
2023/04/25 |
0 |
1 |
… |
0 |
0 |
Table 8.
Maintenance Groups Selected From Sub systems
|
Group |
Sub System |
|
A |
B/E BUCKET & CHAIN DEVICE, BOOM SLEW STRUCTURE |
|
B |
B/E STRUCTURE, BOOM CONVEYOR SYS, GANTRY CONVEYOR SYS, HPP 2 SYS |
|
C |
HPP 1 SYS |
|
D |
MAGNETIC SEPARATOR, B/E DRIVE SYS, B/E SLEW DEVICE, BOOM SLEW DEVICE, BOOM STRUCTURE, GANTRY TRAVEL DRIVE SYS, GANTRY TRAVEL STRUCTURE, HPP 3 SYS, HPP 4 SYS, HPP 5 SYS |
Table 9.
Maintenance Cycle and Range within Maintenance Group A
|
Sub system |
Lower Maintenance Point |
Standard Maintenance Cycle |
Upper Maintenance Point |
Lower Maintenance Bound |
Upper Maintenance Bound |
|
B/E BUCKET & CHAIN DEVICE |
38 days |
53 days |
73 days |
−15 days |
+20 days |
|
BOOM SLEW STRUCTURE |
35 days |
49 days |
69 days |
−14 days |
+20 days |
Table 10.
Facility Maintenance Plan System
Algorithm 2.
Facility Maintenance Plan System |
|
Input:
|
MG: Maintenance Group |
|
SCsys: Standard Maintenance Cycle of system |
|
LBsys: Lower Maintenance Bound of system |
|
UBsys: Upper Maintenance Bound of system |
|
|
Output:
|
SS: Standard System in Maintenance Group |
|
SMR: Simultaneous Maintenance Range |
|
NSCsys: Next Standard Maintenance Cycle of system |
|
|
Procedure:
|
1. Select Standard System within Maintenance Group
|
|
For n in MG : return SS = arg min (SCn)n
|
|
2. Calculate Simultaneous Maintenance Range
|
|
tmp = 0For n in (MG-SS) : If, SCn + LBn ≤ SCSS + UBSS If, tmp < (SCn + LBn) tmp = (SCn+LBn) SMR = tmp ≤ t ≤ SCSS + UBSS
|
|
3. Calculate Next Standard Maintenance Cycle
|
|
For n in (MG-SS) : If, SCn + LBn ≤ SCSS + UBSS med=tmp+(SCSS+UBSS)2 NSCsys=med+SCn Else, NSCsys=SCn
|
|
4. Update SC as NSC & Repeat Step 2,3 until Maintenance plan scope
|
|
|