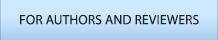1. 서 론
항공기를 개발하는 과정에서 고객의 요구사항을 충족한다는 것을 입증하기 위하여 많은 비행시험을 하게 된다. 비행시험은 고 비용을 요구할 뿐만 아니라 개발 일정에 큰 비중을 차지하므로 효과적인 비행시험을 수행하는 것만으로도 비용절감 및 일정단축에 기여할 수 있다. 최근에는 계측 기술이 발달함에 따라 비행시험 전 과정에 걸쳐서 다양한 변수에 대한 대용량의 데이터가 수집되고 있다. 이러한 비행시험 데이터를 분석하면 항공기의 형상, 성능, 운용 범위 등을 과학적으로 결정할 수 있어서 경제적인 비행시험이 가능하게 된다.
국내 기술로 개발한 수리온 헬리콥터의 경우, 개발과정에서 2년의 비행시험 기간 동안 약 1800소티(sortie; 비행 시험횟수 단위)의 비행시험을 수행했는데, 이중 진동 비행시험이 전체의 20%를 차지한다. 이는 비행시험 진입단계에서 수립한 계획의 10배에 달하는 것으로서, 예기치 못한 이상 현상, 시행착오에 따른 오류 등이 크게 영향을 미쳤지만, 보다 근본적인 원인은 비행시험을 체계적인 시험계획 및 분석기법에 근거하지 않고 수행한 것이다.
수리온 비행시험을 수행한 것을 살펴보면, 우선 비행시험 진입단계에서 계획된 진동저감 형상은 4가지이며 형상 별로 몇 가지 수준을 두어 총 8가지 형상에 대해 30소티를 계획했다. 그러나 진동분석을 위한 비행영역을 확보하기도 전에 예측 범위를 벗어난 과도 진동이 발생하여 초기 비행 계획과는 무관하게 진동저감(Vibration Reduction) 장치를 적용하게 되었다. 따라서 국부적인 진동 현상에 근거하여 비행시험 형상을 결정하게 되었으며 시험 순서는 신속한 시험 진행을 위해 항공기 작업 편의성과 신속성에 중점을 두어 결정하게 되었다. 시험 결과의 분석 또한 국부적 진동 현상 해소에 중점을 두어 수행함에 따라 종합적인 결과 분석에 필요한 시험 조건과 그에 따른 데이터가 누락되어 동일한 형상에 대해 재시험을 하거나 유사조건에 대한 시험을 반복하는 사례가 발생하였다. 그 결과 초기 계획 대비 10배에 달하는 시험을 수행하게 되었다. 수리온에서 수행된 비행시험 내역은 <Figure 1>과 같다. 진동 비행시험 중 가장 비중이 큰 시험 항목은 진동형상 최적화로 전체의 52%에 해당한다.
본 논문에서는 수리온 헬리콥터를 개발하는 과정에서 나타난 진동저감을 위하여 동체의 형상을 변경하며 수행한 비행시험 데이터를 그래프 기법과 호감도 함수를 이용하여 체계적으로 분석하여, 진동저감을 최소화하는 설계조건을 제시하였다. 그래프 분석은 통계소프트웨어인 MINITAB 16®을 이용하였다 (Minitab, 2010). 2절에서는 헬기의 주요 3가지 진동 요인과 제어방법을 소개하고, 그래프를 이용한 진동데이터 분석 방법은 3절에 기술한다. 4절에는 여러 위치에서 측정한 진동수준의 만족도를 하나의 수치로 나타내기 위하여 도입한 호감도 함수를 이용한 수리온의 최적 형상을 제시하며, 5절에서는 결론을 서술하고 추후 연구방향을 제안한다.
2. 수리온 진동 요인 제어 방법
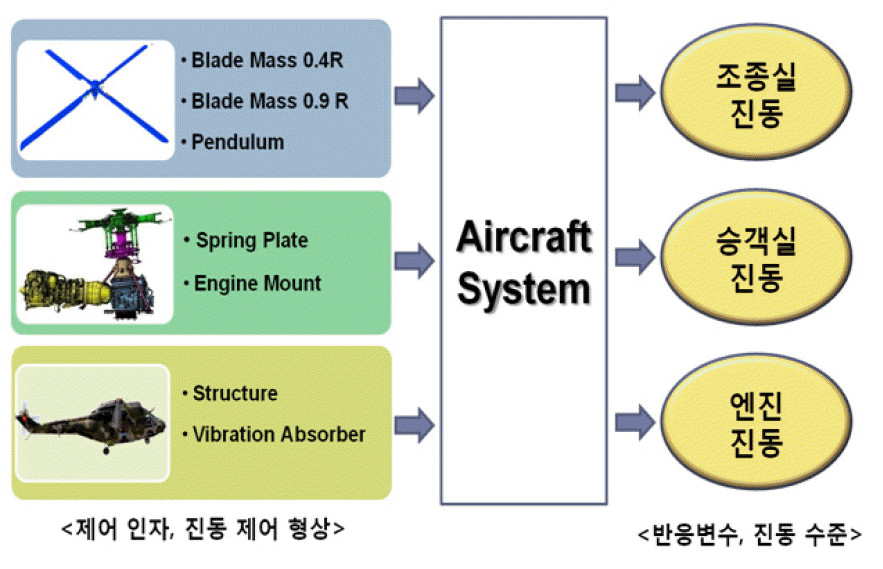
헬기의 진동원은 주로터 시스템으로서, 회전에 의해 동적 하중이 발생한다. 동적 하중은 트랜스미션을 거쳐 엔진을 포함한 항공기 구성품 및 기체 구조로 전달된다. 이러한 진동은 구성품의 수명을 단축시키고 승무원의 피로를 유발해 임무 수행능력을 저하한다. 동체 진동을 유발하는 블레이드 하중의 주요 성분은 주로터 회전속도(Ω)에 비례하여 3Ω, 4Ω, 5Ω으로 나타나는데, 이들은 모두 동체에 4Ω 성분으로 변환되어 전달된다. 주요 진동 성분인 4Ω 주파수 진동을 저감하기 위해 주로터 블레이드, 주기어박스 지지부, 조종실(Cockpit), 객실(Cabin)에 진동저감 장치가 장착되어 있다(Jung et at., 2013). 따라서 수리온에서 주 진동요소는 조종실, 객실 및 엔진의 진동이며, 여러 가지 진동 저감 형상의 최적화를 통해 주요 위치에서의 진동이 최소가 되도록 해야 한다. 참고문헌과 헬기 개발사업에서 진동 수준을 평가하는 일반적인 절차에 따라 헬기의 진동 제어 방법은 다음과 같이 크게 세 가지로 구분된다(Loewy, 1984; Reichert, 1981).
1) 로터 시스템에서 가진원 제어
로터 시스템에서 발생하는 진동하중을 최소화하는 방법으로 블레이드의 진동특성을 변경하거나 진동하중을 상쇄시키는 방법을 적용한다. 수리온의 경우 블레이드 0.4R 위치와 0.9R 위치에 질량을 적용하여 블레이드 진동특성을 변경하는 방법과 펜듈럼(Pendulum)을 장착하여 블레이드 플래핑(Flapping)으로부터 발생하는 하중을 상쇄시키는 방법을 사용하였다.
2) 트랜스미션부에서 진동 전달 특성 제어
트랜스미션은 로터 시스템에서 발생된 진동하중의 전달 경로로서 진동 하중의 전달률을 감소시키는 방법이다. 수리온의 경우, 기체는 트랜스미션 하부에 장착된 스프링 플레이트(Spring Plate), 엔진은 장착 마운트(Mount)의 강성을 조절하여 진동을 제어하였다.
3) 기체에서의 진동 제어
기체는 로터 진동하중에 대한 응답이 최소가 되는 구조가 되도록 설계하였다. 국부적으로 진동이 높거나 안락한 진동특성이 요구되는 경우 스프링-질량 시스템을 장착하여 진동을 저감하는 것이 일반적이다.
수리온 진동시험의 제어인자는 <Table 1>과 같이 정리할 수 있다.
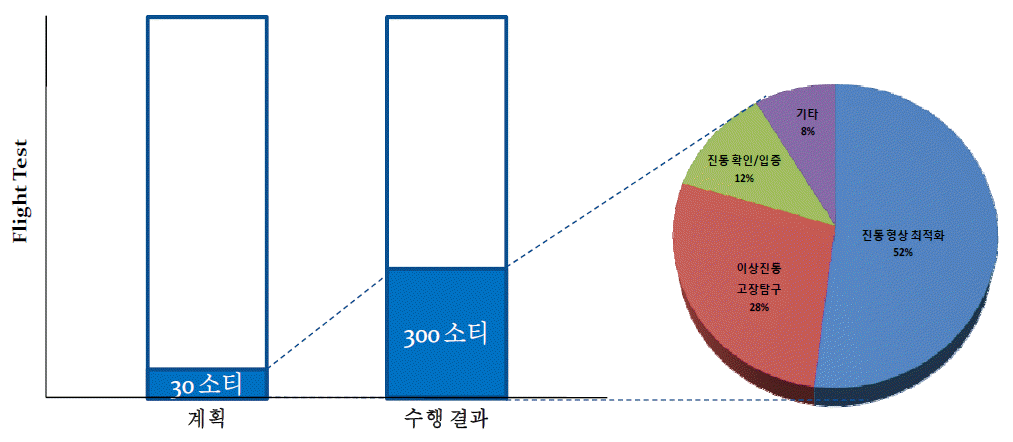
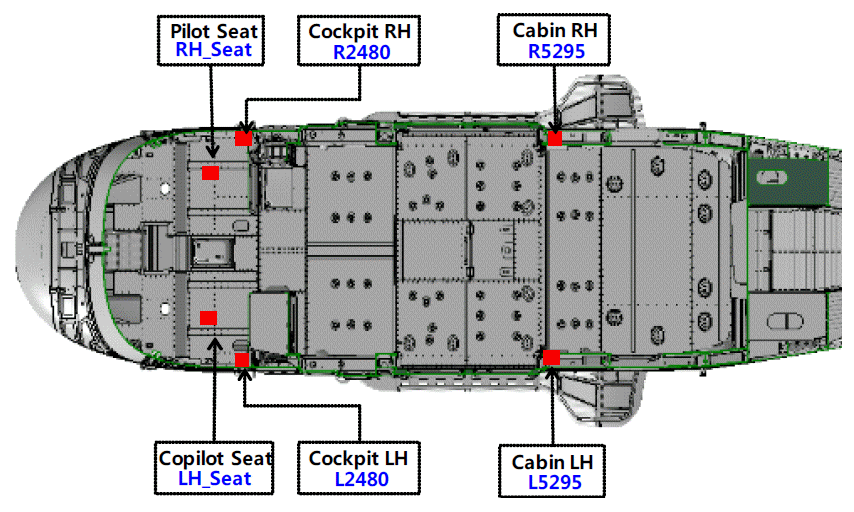
본 연구에서 고려한 비행시험의 성능 척도는 기체와 엔진에서의 진동 수준이다. 기체 진동은 조종실과 객실의 진동으로 조종좌석, 조종실 프레임, 객실 프레임 바닥의 수직방향 성분이며, 진동수준의 측정 위치는 <Figure 2>에 나타내었다. 엔진의 진동수준 측정 위치는 <Figure 3>에 제시하였으며, 좌우 엔진의 종/횡/수직방향의 총 6개의 진동 성분을 성능 척도로 삼는다. 성능 척도인 반응변수는 <Table 2>에 나타낸 바와 같다. 따라서 수리온 진동시험의 제어인자와 반응변수는 <Figure 4>의 Block Diagram으로 제시할 수 있다.
3. 수리온 진동비행시험 데이터 분석
수리온 진동시험은 기본적으로 실험계획에 근거하여 실험한 것이 아니라 헬기 개발사업에서 진동수준을 평가하는 일반적인 평가방법을 토대로 엔지니어들의 경험과 지식을 바탕으로 기본적으로 1회 1인자 실험에 근거하여 제어인자의 수준을 바꾸어 가면서 실험을 하였다. <Table 3>에 비행번호(Flight Number)에 따른 제어인자의 수준과 진동 제어형상을 나타내었다.
수리온 진동저감을 위하여 수행된 진동비행시험 데이터를 이용하여 다음과 같이 4가지 측면에서 그래프 분석을 수행하였다.
(1) 각 부위별 진동수준 간 상관성 파악
(2) Flight Number별, 비행속도 변화에 따른 각 부위 진동수준 추이
(3) 인자의 영향도 파악
(4) 규격(진동수준 ≤ 1.0) 만족 형상 파악
3.1 각 부위별 진동수준 간 상관성
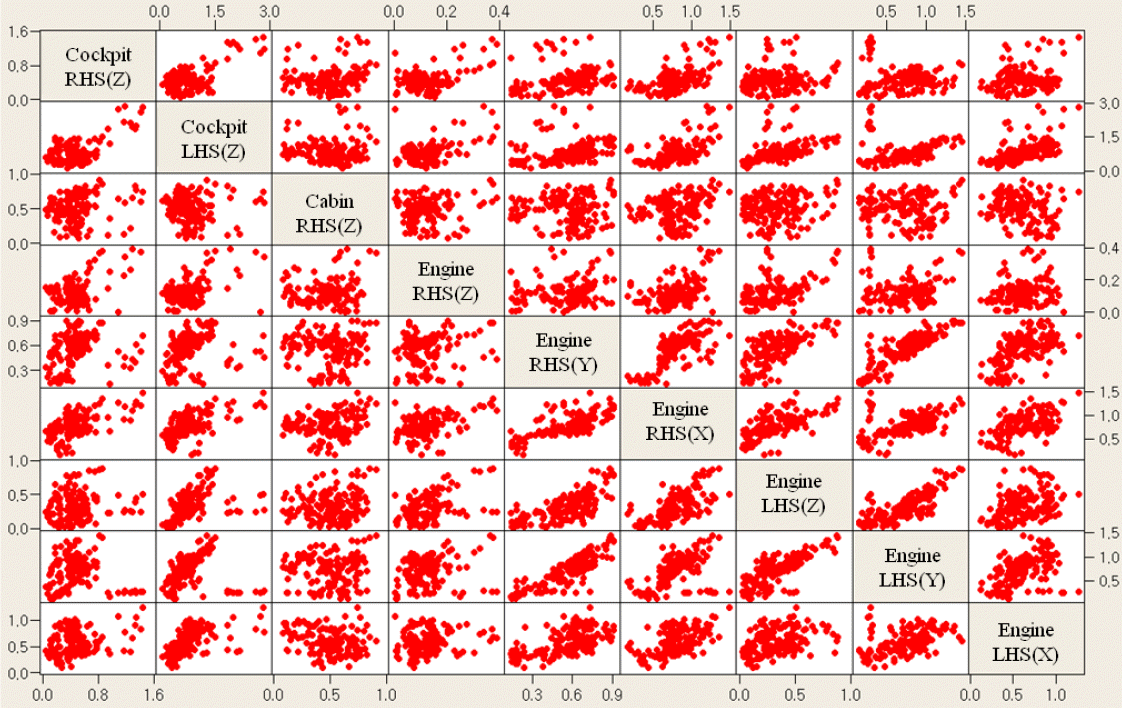
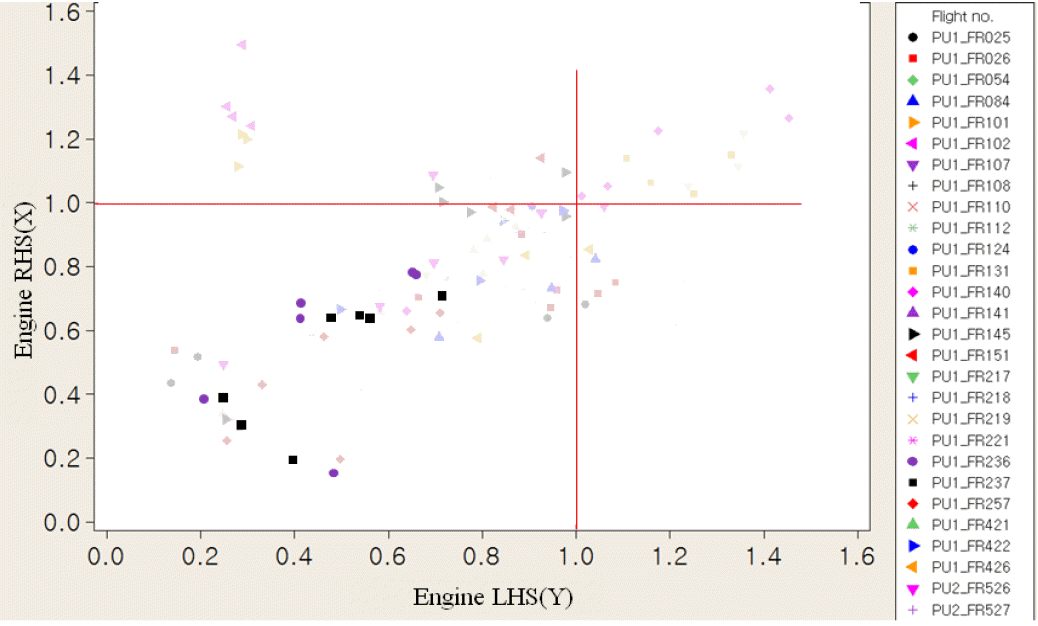
상관성 분석은 진동하중의 전달경로를 분석하는 데에 도움이 되고, 진동하중의 흐름을 분석하면 진동저감장치의 장착 위치를 정하는 데 유리하다. 주요 부위별 진동수준간 상관성을 <Figure 5>에 나타내었는데, 객실(Cabin)의 경우, 좌우측 진동수준이 거의 비슷하게 나타나므로 객실 오른쪽 Z 방향 진동수준인 객실(Z)만 분석 대상으로 삼았다. <Figure 5>를 보면, 엔진 우측의 Y축 진동수준인 Engine RHS(Y)는 우측 X축인 Engine RHS(X), 좌측 Z축과 Y축 진동수준인 Engine LHS(Z), Engine LHS(Y)과 상관성이 높다는 것을 알 수 있다. 이는 어떤 제어인자의 수준을 변경함으로써 Engine RHS(Y)의 값을 줄일 수 있으면 다른 3개의 진동수준 값도 함께 개선될 수 있음을 시사한다. 반면에 엔진 우측 Z축과 엔진 좌측 X축 진동수준인 Engine RHS(Z)과 Engine LHS(X)는 엔진의 다른 진동수준과 상관성이 없거나 미약하다. 조종실 우측과 좌측의 Z축 진동수준인 Cockpit RHS(Z)과 Cockpit LHS(Z) 간에도 상관성이 있다.
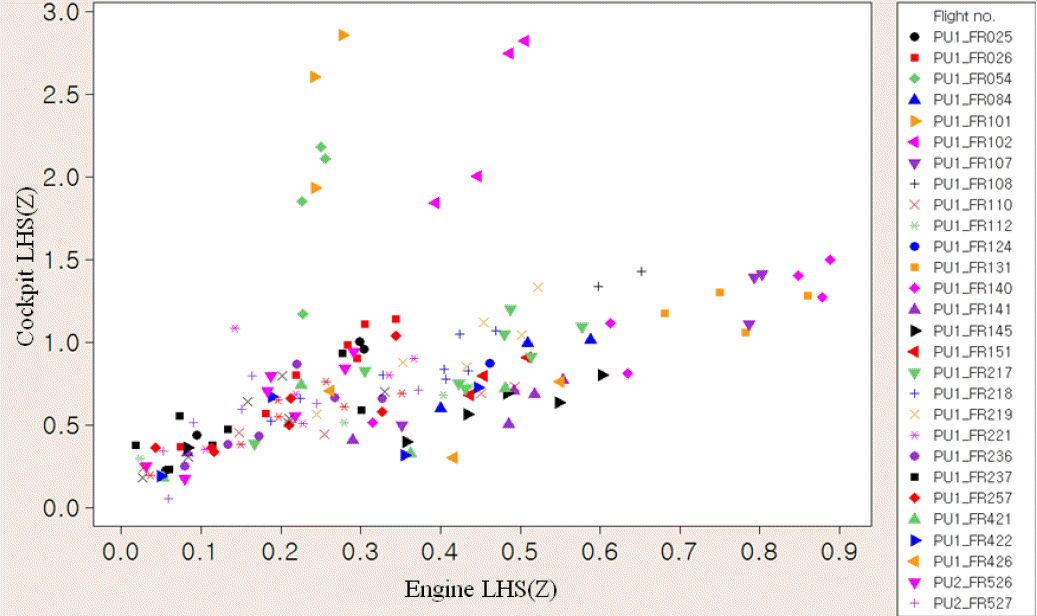
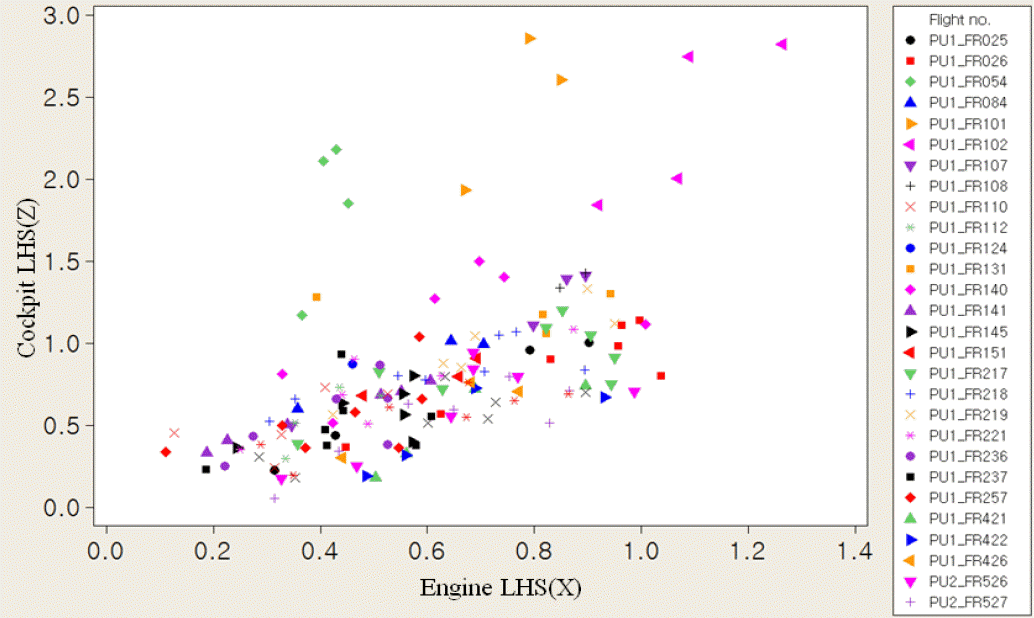
상관성이 없는 객실 진동은 분석 대상에서 제외하였고, <Figure 6> ~ <Figure 9>에는 주요 진동부위별 상관성을 형상조건에 따른 비행번호별로 나타내었다. <Figure 6>을 보면, Flight No. PU1_FR(이하 생략) 054, 101, 102를 제외하면 두 진동수준 간 상관성이 아주 높다. 그리고 Flight No. 054, 101, 102의 비행시험조건에서 조종실 좌측 Z-축 방향의 진동수준은 아주 높고 엔진의 좌측 Z-축 방향은 아주 낮게 나타난다.
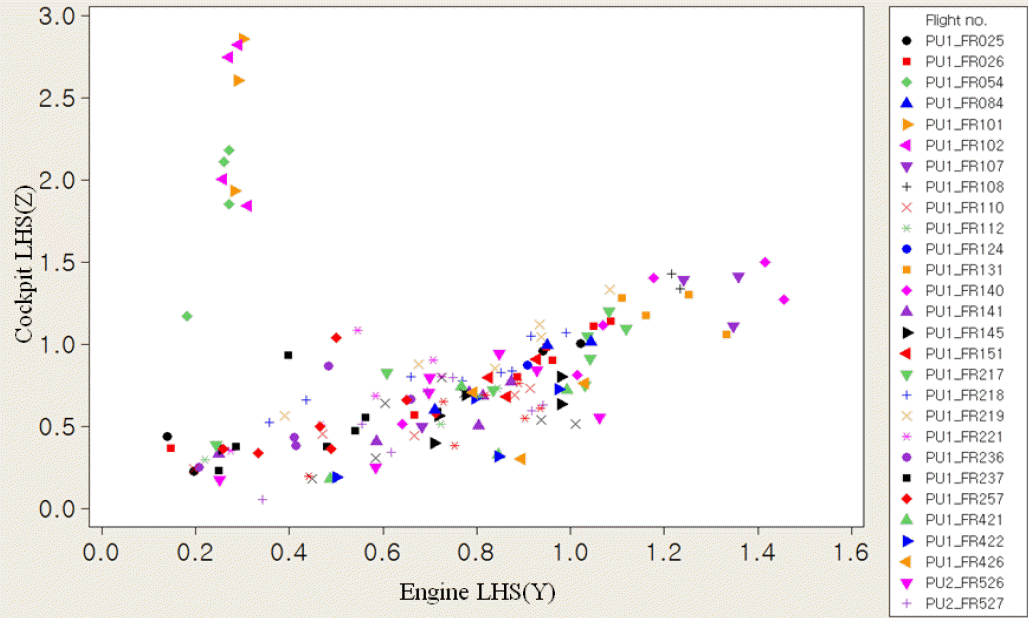
Cockpit LHS(Z)와 Engine LHS(Y) 간 상세한 상관성 그림을 <Figure 7>에 나타내었는데, 여기서도 Flight No. 054, 101, 102를 제외하면 두 진동수준간 상관성이 높게 나타나며, 이들 조건에서는 Cockpit LHS(Z)의 진동수준은 아주 높고, 엔진의 좌측 Y-축 방향 진동수준인 Engine LHS(Y)는 아주 낮다.
<Figure 8>에는 Cockpit LHS(Z)와 Engine LHS(X) 간 상세한 상관성 그림을 나타내었다. 여기서도 Flight No. 054, 101, 102를 제외하면 두 진동수준 간 상관성이 있는데, <Figure 6>이나 <Figure 7> 보다는 낮게 나타난다. Flight No. 054, 101, 102 조건에서는 Cockpit LHS(Z)의 진동수준은 아주 높고, Engine LHS(X)의 진동수준은 낮다. <Figure 6>, <Figure 7>, <Figure 8>에서 조종실의 진동수준을 높게 만드는 Flight No. 054, 101, 102의 공통점은 Engine Mount가 모두‘Rigid’가 아니고, ‘Soft’임을 알 수 있다(<Table 3>).
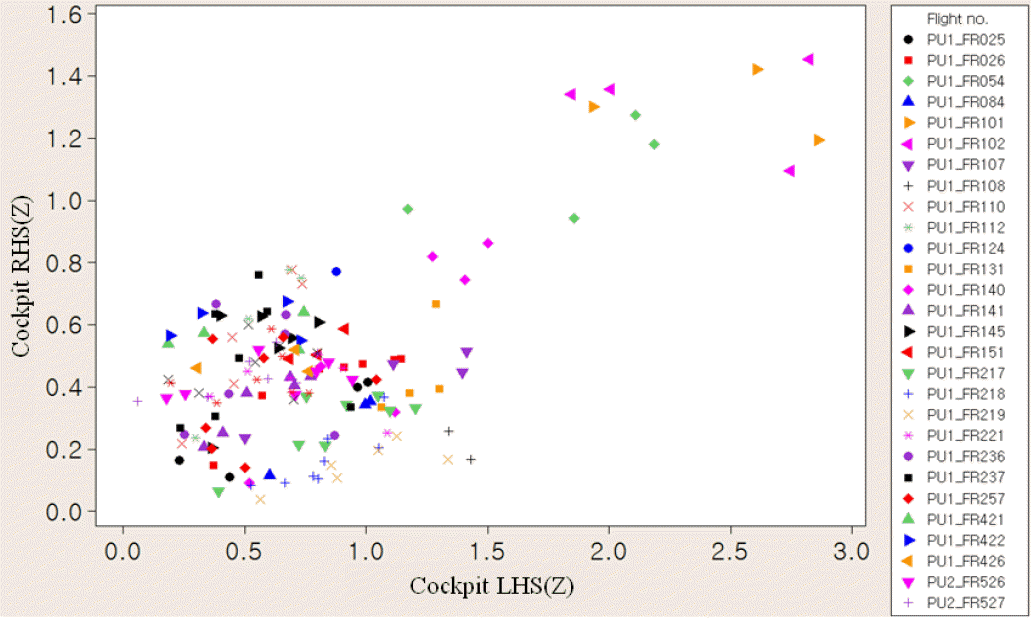
<Figure 9>에 조종실의 좌우측 진동수준의 상관성을 그림으로 나타내었는데, Engine Mount가 'Soft'인 Flight No. 054, 101, 102에서 Cockpit RHS(Z)와 Cockpit LHS(Z) 모두 진동수준이 아주 높게 나타남을 알 수 있다. 그리고 이들 비행시험 조건을 제외하면 조종실의 양쪽 위치에서의 진동수준 간에는 상관관계가 없음을 알 수 있다. <Figure 6> ~ <Figure 9>에서 제어인자에 따라 상관성이 달라지는 이유는 진동저감 장치 형상에 따라 진동하중 전달 특성이 달라지기 때문이다.
3.2 비행속도에 따른 진동수준
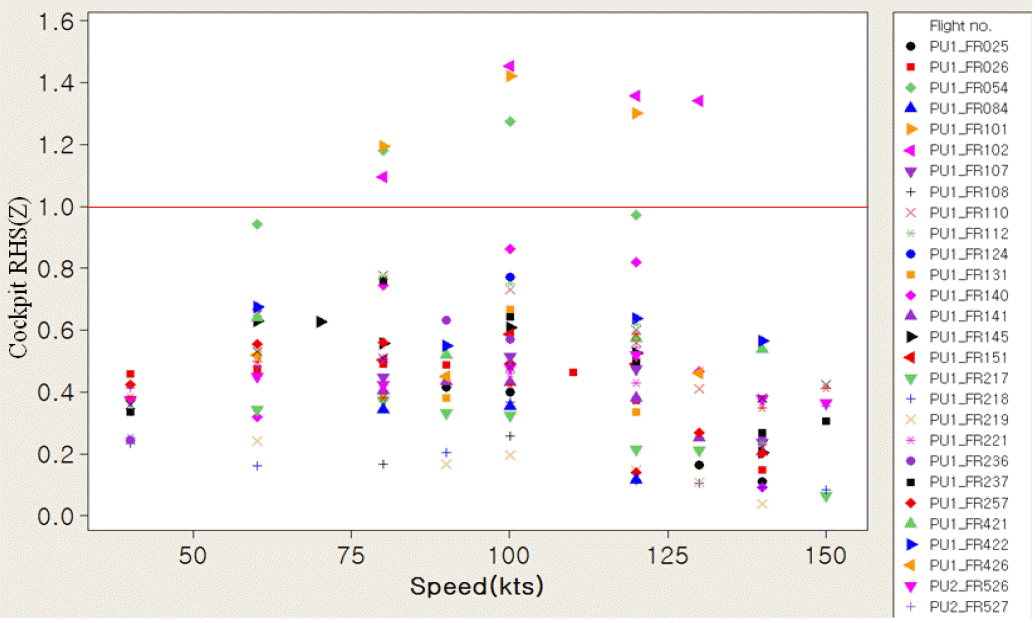
수리온 비행시험 데이터를 이용하여 비행속도에 따른 진동수준의 변화도 그래프 분석을 통하여 나타낼 수 있다. <Figure 10>을 보면, 비행속도가 낮거나 높을 때 보다는 75~125kts 사이인 중간 정도 속도에서 조종석 오른쪽 진동수준인 Cockpit RHS(Z)가 더 높다는 것을 알 수 있다. 객실과 엔진에 대해 분석한 결과에서도 각 진동수준은 이와 비슷한 형태로 나타났다.
이와 같이 비행속도에 따른 그래프를 이용하여 Cockpit RHS(Z), Cockpit LHS(Z), Cabin RHS(Z), Engine RHS(Z), Engine RHS(Y), Engine RHS(X), Engine LHS(Z), Engine LHS(Y), Engine LHS(X)의 진동수준을 살펴보면, 다음의 사실을 알 수 있다. 객실의 진동수준인 Cabin RHS(Z)와 엔진의 3가지 진동수준인 Engine RHS(Z), Engine RHS(Y), Engine LHS(Z)는 규격을 만족하고, 조종실의 좌우측 진동수준인 Cockpit RHS(Z), Cockpit LHS(Z)와 엔진의 Engine RHS(X), Engine LHS(Y), Engine LHS(X)의 진동수준은 규격을 만족하지 못한다. 여기서 규격을 만족한다는 말은 모든 비행속도에서 해당 진동수준이 규격 안에 들어온다는 것을 의미한다.
3.3 주요 부위별 비행시험 조건에 따른 진동수준
각 부위의 진동수준을 규격인 1.0 이하로 유지하기 위한 시험비행 조건을 파악하기 위하여 3.2절의 그래프 분석방법을 이용하면, 진동수준이 규격을 만족하지 못하는 5곳의 부위 중에서 Cockpit RHS(Z)과 Engine LHS(X)의 경우, Engine Mount가 'Soft'인 조건인 Flight No. 054, 101, 102를 제외하면 진동수준이 규격 안에 들어온다. 따라서 Engine Mount를 'Rigid'로 정하고, 규격을 많이 벗어나는 진동수준인 Cockpit LHS(Z), Engine RHS(X)를 Engine LHS(Y)과의 산점도를 통하여 진동수준이 규격을 만족하는 비행시험 조건을 구하면 된다.
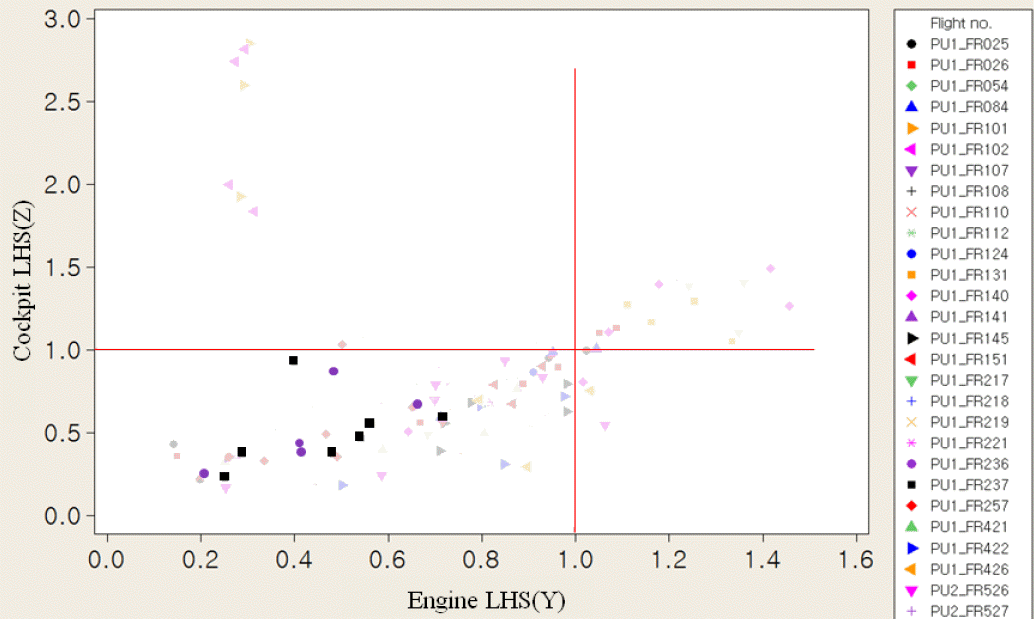
Cockpit LHS(Z)와 Engine LHS(Y)의 산점도를 나타낸 <Figure 11>을 보면, 두 부위의 진동수준 규격인 1.0 내에 들도록 하는 비행시험 조건은 Flight No. 110, 112, 124, 141, 145, 151, 236, 237, 422, 527이다. 여기서 밑줄친 비행시험 조건인 236, 237에서는 비행속도에 관계없이 진동수준이 안정적으로 1.0 이하로 유지된다. <Figure 12>의 Engine RHS(X)와 Engine LHS(Y)의 산점도로부터 Flight No. 110, 112, 141, 218, 221, 236, 237, 257, 527 조건에서 Engine RHS(X)와 Engine LHS(Y)의 진동수준이 규격에 들어오고 밑줄 친 221, 236, 237, 257 비행 조건에서 비행속도에 관계없이 진동수준이 안정적으로 1.0 이하로 유지된다. <Figure 11>와 <Figure 12>로부터, 진동수준이 안정적으로 1.0 이내에 들도록 하는 시험비행 조건은 Flight No. 236, 237이다. 즉, Vibration Absorber의 수준을 감안하지 않으면, 수리온 진동저감 시험비행 데이터에 근거한 최적형상은 (Blade Mass 0.4R, Blade Mass 0.9R, Pendulum, Spring Plate, Engine Mount) = (–, –, c, Normal, Rigid)임을 알 수 있다.
4. 호감도 함수를 이용한 진동수준 평가기법
4.1 종합 호감도 산출
제품 개발을 위해 성능시험을 할 때에 일반적으로 고려되는 성능특성은 하나가 아니라 두 개 이상인 경우가 대부분이다. 수리온 헬리콥터 개발의 경우 진동수준을 최소화하기 위해서는 한 위치가 아니라 여러 위치의 진동수준을 측정하는데, 그들이 각각 최소한 일정한 수준 값 이하로 그리고 가능한 작은 값을 유지하도록 해야 한다.
이러한 다수 특성치의 문제는 각 특성(반응변수) 별로 최적수준이 일치하지 않기 때문에 실험인자의 조건을 쉽게 결정할 수 없게 된다. 수리온 헬기의 진동은 3군데 위치, 즉, 조종실, 객실, 엔진에서 측정을 하는데, 조종실과 객실의 경우에는 Z축 방향, 좌, 우 엔진은 각각 3가지 방향(X, Y, Z축)의 진동 수준을 일정한 값 이하로 유지해야 한다. 문제는 어느 한 위치에서의 진동수준 값을 줄이기 위하여 진동저감 장치에 변화를 주거나 인자의 값을 바꾸면 다른 쪽 부위의 진동이 높아지는 상충현상(Conflict Phenomenon)이 생긴다는 것이다. 예를 들어, 엔진의 진동을 줄이기 위하여 Rigid 마운트를 Soft 마운트로 바꾸면 엔진진동은 줄어들지만, 다른 부위의 기체진동은 더 심해지는 현상이 발생한다. 이와 같이 다수 반응변수를 고려하는 실험의 경우, 어떤 인자의 최적조건이 반응변수 별로 다르게 되는 상충 현상이 나타나게 되는데, 이런 경우에 우선 각 실험조건에서 나온 반응변수의 값을 바탕으로 그 조건의 종합적인 우월성을 판단하는 척도가 우선 필요하며, 각 실험조건의 데이터를 바탕으로 이러한 척도를 최적화 하는 절충최적조건(Compromised Optimal Condition)을 구해야한다.
본 연구에서는 헬리콥터의 진동수준을 나타내는 척도로서 호감도 함수(Desirability Function)를 사용하였다(Derringer and Suich, 1980). 이 접근방법에서는 각각의 반응변수 별로 호감도 함수를 구하고, 이러한 호감도의 기하평균을 이용하여 종합 호감도(Overall Desirability)를 구하며, 종합 호감도를 최대화하는 조건이 최적 조건이 된다. 이 문제에서 반응변수는 각 측정점에서 측정한 진동 수준이고, 반응변수의 값은 작을수록 좋으며, 값의 상한(Upper Limit)이 주어져 있다. 이 경우 반응변수 에 대한 호감도는 다음과 같이 나타낼 수 있다.
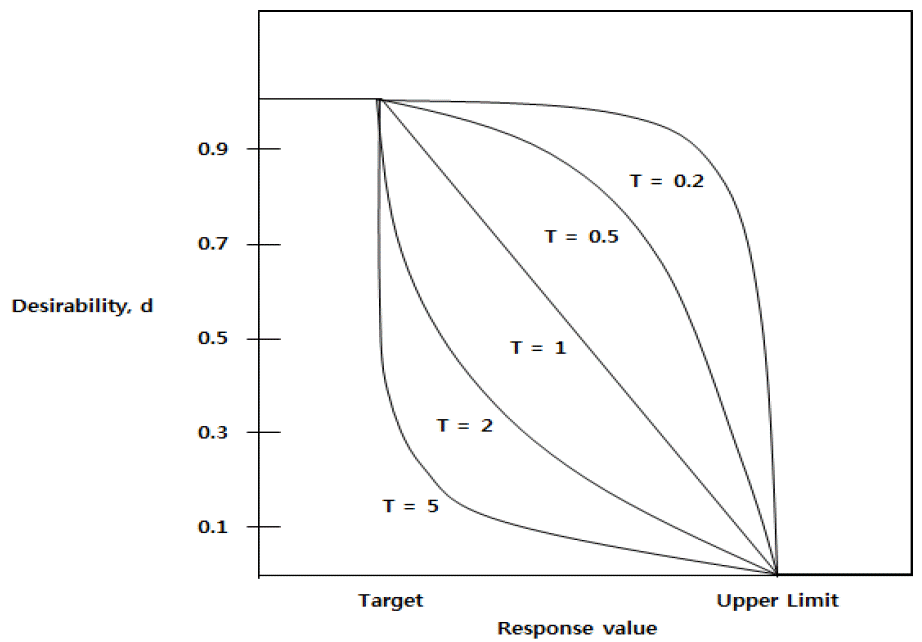
식 (1)에서 B와 C는 각각 목표값과 상한인데, 본 논문에서는 0과 1이다. 반응변수의 값이 목표값에 이르면 호감도는 최대값인 1이 되고, 반응변수의 값이 상한보다 크거나 같으면 호감도는 0이 된다. 지수 T는 반응변수에 대한 가중치(Weight)이며 T=1이면 한계로부터 목표값까지의 호감도 함수는 직선 형태를 가지고, T<1일 때에는 반응변수의 값이 한계 내에 있으면 호감도는 T=1인 경우보다 더 높은 값을 갖는다. <Figure 13>은 상한만을 가지는 경우 가중치와 호감도의 관계를 나타내고 있다.
본 논문에서는 조종실과 객실에서의 진동 수준 변수 Yi에 대한 호감도에는 가중치 1을 사용하였고, 엔진의 진동 수준은 1.0 이내에만 들어오면 충분히 만족스럽다고 생각되어 가중치 0.1을 사용하였다.
각각의 반응변수에 대한 호감도가 d1, d2, d3, •••,dn이라면 종합 호감도는 다음과 같이 계산된다.
식 (2)와 같이 기하평균을 이용하여 종합 호감도를 계산하는 이유는 다수의 반응변수들 중에서 하나의 반응변수라도 한계 내에 들지 못하는 경우가 발생하면, 종합 호감도를 0으로 만들 수 있기 때문이다. 이렇게 하면 하나의 제품이 많은 성능특성을 가지고 있다고 가정할 때, 하나의 성능특성이라도 규격 내에 들지 못하는 경우, 종합 호감도가 0이 되어 그 제품은 불량품이 되도록 만들 수 있다.
4.2 수리온 데이터의 호감도 함수 분석
수리온 비행시험을 수행한 데이터를 가지고 비행번호(Flight Number)에 따른 종합 호감도(Overall Weighted Desirability)를 계산하여 <Table 4>에 나타내었다.
<Table 4>의 종합 호감도 값은 다음의 같이 호감도 함수를 계산하여 산출하였다. 조종실(Cockpit)과 객실(Cabin), 엔진(Engine)의 3개의 진동수준 변수에 대해서, 진동수준 변수 Yi의 호감도 Des_Yi는 다음과 같이 구한다.
엔진의 진동수준은 1.0 이내에만 들어와도 충분히 만족스럽다고 생각하므로, 엔진의 6개 진동수준 변수에 대한 호감도를 구할 때에는 가중치를 반영한 Yi의 호감도 Des_Wt_Yi는 가중치를 0.1로 두어 다음과 같이 구한다.
식 (3)과 (4)를 이용하면 종합 호감도는 다음의 식 (5)와 같이 산출할 수 있다.
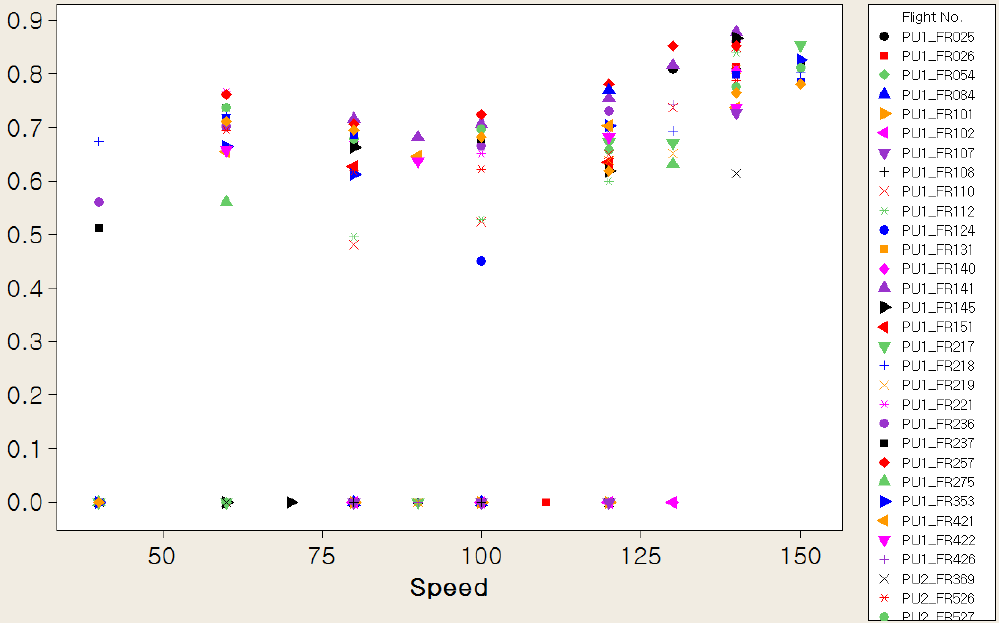
비행시험 조건 별로 종합 호감도의 값을 <Figure 14>에 나타내었다. <Figure 14>를 보면, 다양한 시험비행 속도에서 꾸준하게 종합 호감도의 값이 크게 나타나는 시험비행 조건은 Flight No. 141, 236, 237, 257, 421, 422, 527, 532이다. 여기서 밑줄 친 조건은 어떤 비행속도에서 종합 호감도가 0인, 즉 진동수준이 1.0을 초과하는 것을 나타낸다.
비행속도에 따른 종합 호감도의 변화를 <Figure 15>에 나타내었는데, 전반적으로 비행속도가 빨라지면 호감도가 다소 높아지고, 특히 속도가 140이상이 되면 종합 호감도가 0이 되는 경우는 발생하지 않음을 알 수 있다.
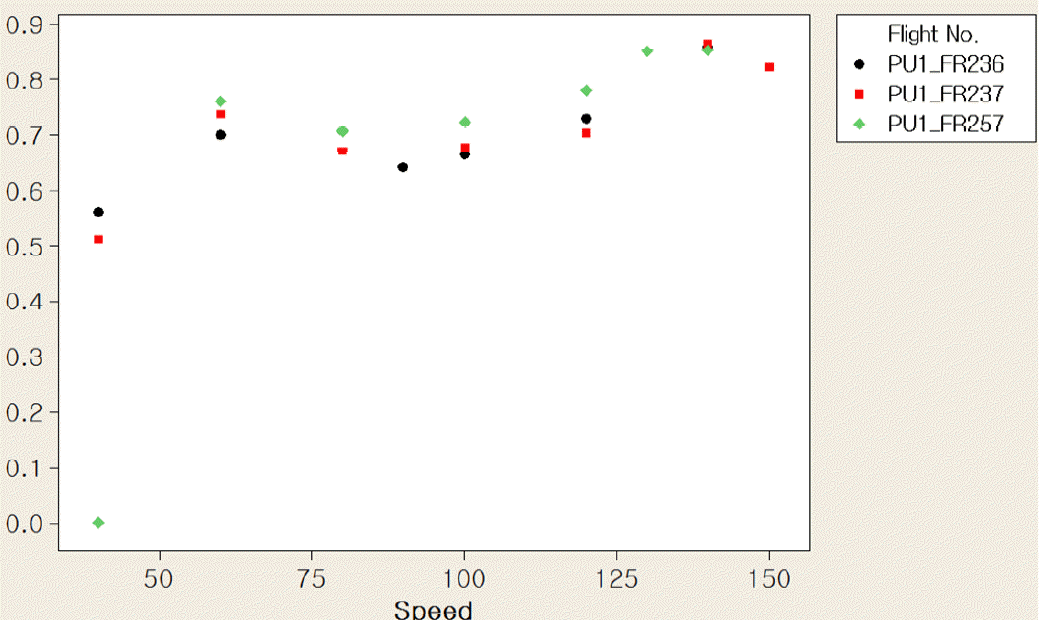
높은 호감도를 나타내는 3가지 비행시험 조건인 Flight No. 236, 237, 257을 대상으로 비행속도에 따른 종합 호감도의 변화를 <Figure 16>에 나타내었고, <Table 5>는 그 때의 진동저감 형상 조건을 보여준다. 한 가지 눈 여겨봐야 할 것은 Flight No. 257의 경우, 비록 비행속도가 40일 때에는 호감도가 0이지만 그 외의 경우에는 호감도가 다른 조건 보다 더 높다는 것을 알 수 있다. 만일 비행속도 40에서 조종사의 실수로 인하여 호감도가 0, 즉 진동수준이 규격을 벗어나서 높게 나온 것이고, 차후 이러한 실수를 예방할 수 있다면 Flight No. 257의 조건도 좋은 진동저감 형상으로 생각할 수 있다. 최종적으로 선정된 진동저감 형상은 보다 안정되게 진동을 저감하기 위하여 조종실의 좌·우측에 Vibration Absorber를 고수준(+)으로 설정한 Flight No. 237의 조건이다. 우선 257 형상은 호감도가 0인 경우가 있으므로 배제하였고, 236 조건에서는 비행시험 데이터가 충분하지 않았다.
5. 결론과 추후 연구방향
본 논문에서는 수리온 헬리콥터 개발 시 중요한 문제인 진동저감을 위한 방법으로서 그래프 분석과 다수의 성능특성에 대한 요구를 충족시키는 방법 중 하나인 호감도 함수를 이용하여 진동데이터를 분석하고 진동수준을 낮출 수 있는 진동제어 인자들의 최적조건을 찾는 과정을 사례로 제시하였다. 수리온의 진동수준은 조종실, 객실, 엔진에서 측정하였는데, 측정된 진동 수준은 정해진 규격 이하의 값을 가져야 한다. 수리온 진동데이터를 바탕으로 주요 부위의 진동수준 간 상관관계, 시험 형상 별로 비행속도에 따른 진동의 추이, 각 조건에서 9개의 진동 부위의 진동수준으로부터 구한 종합 호감도 값을 이용하여 항공기의 최적 형상을 결정하는 분석 방법을 제시하였다.
본 논문의 시사점은 신제품 또는 체계를 개발함에 있어서 1)시험 데이터의 그래프 분석을 통하여 최적의 제품 또는 공정 조건을 탐색하고, 2)주요 특성의 값을 여러 부위에서 측정해야 할 경우에 이들 측정값을 단일한 척도로 표현하기 위하여 호감도 함수를 방법을 활용함으로써 각 시험조건에서 종합 호감도를 산정함으로써 개발자들에게 종합적인 성능평가기준을 제시할 수 있다는 것이다. 향후 효율적이고 효과적인 헬리콥터 개발시험을 위해서는 비행시험 환경의 일관성 확보해야 하고, 체계적인 실험계획에 의하여 시험을 설계하고 분석하는 것이 필요하다(Byun et al., 2014).