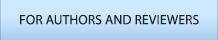통계적 기법을 품질향상 문제에 응용하는 연구 방법론의 한 범주로 확률모형 및 추정분야에서는 산업현장에서 발생하는 다양한 상황에 대하여 확률적인 모형을 설정하고 그 모형의 특징 및 여러 가지 모수, 그리고 관심 있는 확률들을 추정하는 방법들이 고찰되었다. 우리나라에서 이 분야의 연구는 1980년대에 본격적으로 진행되기 시작하여 품질경영학회지를 통하여 다양한 연구결과들이 발표되었다.

먼저 엄태원과 정수일(1981)은 품질특성치(quality characteristic)가 와이블 분포(Weibull distribution)를 따르는 경우 그래픽 방법에 의한 모수추정방법을 고찰하였다. 특히 이 논문에서는 이시카와가 개발한 확률지(probability paper)에 의한 모수추정 방법과 컴퓨터에 의한 추정결과를 비교 분석하여, 산업현장에서 간편하면서도 효율적인 모수추정 방법을 제시하였다. 이 논문과 연관된 연구로 김우철 외 2인(1983)은 형상모수(shape parameter)가 미지인 다수의 와이블 분포에서 최우추정법에 의한 최소의 척도모수(scale parameter)를 갖는 분포의 결정방법을 제시한 후, 기존방법과의 효율성을 비교하였으며 제안된 방법이 쉽게 사용될 수 있도록 연구결과를 수표로 요약하여 제시하였다. 그리고 Lee, Seung-Ho와 Choi, Kook Lyeol(1985)은 감마분포(gamma distribution)의 모수 추정방법을 연구하였다. 이 논문에 저자들은 형상모수(shape parameter)가 이미 알려져 있고 또한 모수 값이 동일한 다수의 감마 분포 중에서 최대의 척도모수(scale parameter)를 갖는 분포의 결정방법을 고찰하였다. 이 연구에서는 먼저 여러 개의 감마분포 중에서 고려대상이 될 수 있는 분포를 먼저 선별 한 후, 선별된 분포를 이용하여 모수를 추정하는 이단계 방법(two stage procedure)이 제시되었다. 그리고 Jeon, Jong Woo et. al.(1986)은 두 개의 지수모집단을 비교하기 위한 점근적으로 유효성을 갖는(asymptotically efficient) 검정방법을 제안하였다. 이 연구에서는 두 개의 지수모집단을 대상으로 위치모수와 척도모수 동시검정에 대하여 Bahadur 효율성의 입장에서 점근적 최적 검정방법이 개발되었다.

정규분포 모형에서 모수추정 방법에 대한 연구로 Lee, Sang-do et al.(1989)는 정규분포 모형에서 모분산을 추정하는 방법을 고찰하였다. 이 논문에서 저자들은 전통적인 최소분산불편추정량의 개념 대신 평균제곱오차(MSE: mean squared error)를 최소화 하는 방법으로 모분산을 추정하는 방법을 연구하였으며, 기존의 방법과 제안한 방법의 효율성을 비교하여, 각각의 추정방법이 언제 효율적인 방법이 되는지에 대한 조건들을 고찰하였다. 한편 Cha, Young Joon과 Lee, Jae Man(1995)은 생존함수(survival function) 모형에서 일반적으로 사용되는 추정량인 Kaplan-Meier 추정량과 Nelson 추정량의 효율성을 비교 고찰하였으며, 표본의 크기가 작은 경우에 붓스트랩(bootstrap)방법을 사용하는 방법 등을 모의실험을 통해 비교하였다. 그리고 Kim, Hwanjoong(2001)은 생존함수 모형에서 NBU(new better than used) 변수에 대한 검정방법을 구하였다. 이 논문에서 저자는 새로운 검정통계량을 제시하고 기존의 Ahmad 방법과 비교 고찰하여 소표본(small sample)인 경우 보다 우수한 방법이 됨을 보였으며 사례분석을 통하여 응용기법을 고찰하였다.

그리고 확률모형에서 확률을 추정하는 방법에 대한 연구로 Kim, Jae Joo와 Kim, Seong Yeon(1986)은 세 개의 확률변수가 확률적으로 독립적인 지수분포를 따르는 경우, 어떤 확률변수가 다른 확률변수 보다 크고, 또 다른 확률변수보다 작을 확률을 추정하는 방법을 연구하였다. 이 연구에서 저자들은 최우추정법과 최소분산불편추정량을 구하는 방법 및 각 추정량의 통계적 특징을 고찰하였다. 그리고 Kim, Jae-Joo와 Kim, Hwan-Joong(1987)은 확률분포가 지수족(exponential family)에 속하는 경우, 어떤 확률변수가 다른 확률변수 보다 작을 확률을 추정하는 방법을 고찰하였다. 특히 이 논문에서는 확률변수가 지수분포를 따르고 다른 확률변수는 정규분포를 따르는 경우 최우추정법과 최소분산불편추정법을 이용한 추정 방법들이 고찰되었으며, 저자들은 모의실험을 통하여 각 추정방법의 효율성을 비교 분석하였다.

한편 Lee, In Suk과 Cho, Jang Sik(1995)은 두 개의 확률변수가 이변량 정규분포를 따르는 경우 어떤 확률변수가 다른 확률변수보다 작을 확률값을 추정하는 방법을 고찰하였다. 이 논문에서는 기존의 방법과는 달리 붓스트랩 기법을 이용한 신뢰구간을 추정하는 방법이 제시되었으며, 모의실험을 통하여 기존의 방법과의 효율성도 비교 고찰되었다. 더 나아가 Lee, In Suk과 Cho, Jang Sik(1997)은 두 개의 확률변수 X, Y가 이변량 정규분포를 따르고, 변수 X, Y 에 영향을 주는 설명변수(explanatory) variable)가 있는 경우 X가 Y보다 클 확률을 추정하는 방법을 연구하였다. 이 논문에서 저자들은 기존의 방법과는 달리 붓스트랩(bootstrap) 방법을 이용하여 확률값의 신뢰구간을 추정하는 방법을 제시하고 모의실험을 통하여 효율성을 비교 분석하였다.

중도 절단된(censored) 자료를 분석하는 통계적 모형에 대한 연구로 Kim, Jae Joo와 Yeom, Joon Keun(1984)은 일반적인 연속형 분포함수 모형에서 중도 절단된 자료를 이용하여 특정 확률변수가 다른 확률변수 보다 작을 확률을 추정하는 방법을 연구하였다. 이 연구에서 저자들은 최우추정법에 의한 추정방법과 추정량의 접근적 분포를 고찰하였으며, 최우추정량과 최소분산불편추정량과의 통계적 효율성을 고찰하여 비교 분석하였다. 그리고 권영일(1987)은 자료가 정규분포를 따르고 사전에 결정된 시점까지의 관측 정보만 사용하는 경우의 모수 추정 방법에 대해 연구하였으며, 최우추정법을 이용하여 추정하는 방법과 중도 절단 형태에 대한 다양한 추정량들의 특징을 모의실험(simulation)을 통하여 비교 분석하였다. 그리고 이 분야의 또 다른 연구로 Cha, Young Joon(1990)은 중도 절단(censored)된 자료의 생존함수(survival function) 모수추정방법을 고찰하였다. 저자는 이 연구에서 생존함수 모형 중 준모수(semi-parametric) 모형인 Cox의 회귀모형의 모수추정방법을 다루었고 추정량의 점근분포(asymptotic distribution)를 고찰한 후, 모의실험을 통하여 소표본(small sample size)인 경우 제안한 기법이 기존의 방법보다 우수한 방법임을 입증하였다. 이와 같은 논문들을 시대 순으로 정리하여 그림으로 요약하면 <Figure 1>과 같다.

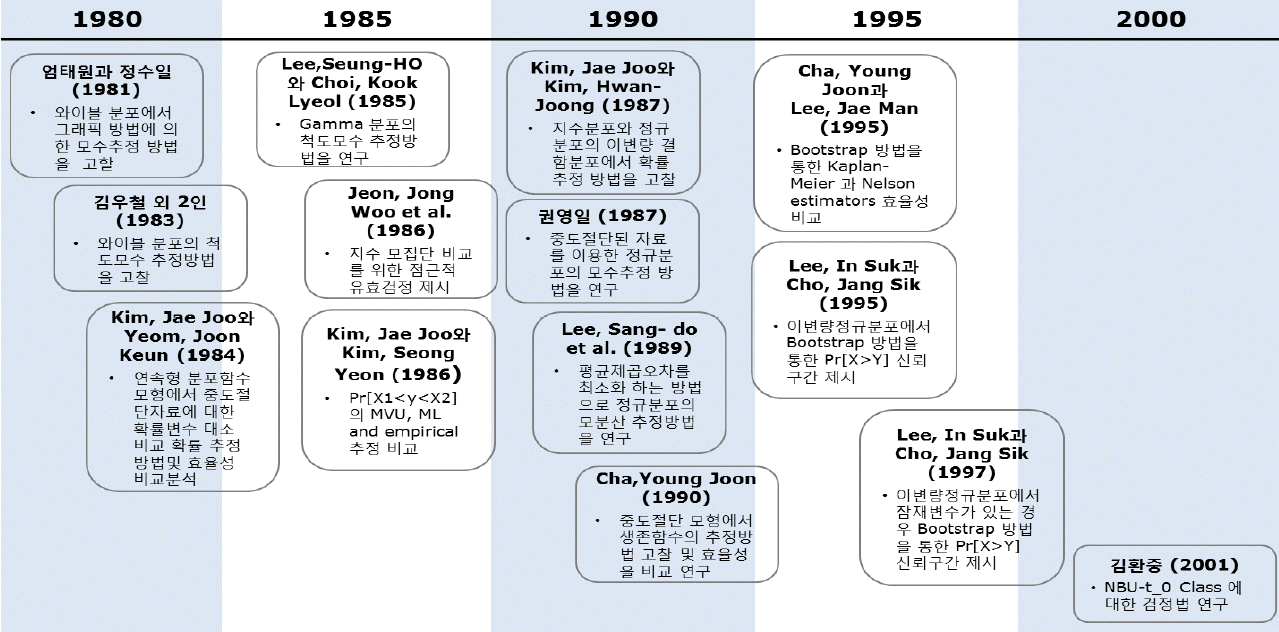
그리고 확률모형의 응용기법에 관한 연구로 Oh, Chung Hwan(1992)은 다시점(multi-states) 마코프 프로세스(Markov process)를 계획하는 방법 및 수학적 표현 방법을 고찰하였다. 특히 시스템에서 각 단위들이 전이되는 비율(transition rate)이 현시점의 상황과 확률적으로 의존적인 다시점 시스템인 경우, 저자는 마코프 프로세스 시스템의 알고리듬을 수학적으로 표기하는 방법을 고찰하고 단순화된 수학적 표현방법을 제시하였다. 그리고 김희철과 이승주(1999)에서는 소프트웨어 신뢰도 분석에서 응용되는 모형인 Jelinski-Moranda 모형, Goel-Okumoto 모형과 Schick-Wolverton 모형에서 Gibbs 샘플링 방법을 이용하여 위험함수의 추정 방법 및 초기 오류수의 형태의 사전분포가 포아송 분포인 경우에 대해 베이지안 추론 방법 및 모형 선택 기법이 고찰되었다. 그리고 남윤석 외 2인(2000)에서는 SAS/ETS 및 SAS/STAT에서 비선형 회귀모형의 모수를 추정하는 원리를 이용하여 복잡한 형태의 비선형 방정식계의 근사적인 해를 구하는 방법이 소개되었다. 이 방법은 알고리즘 구축과 프로그램 작성의 어려움이 따르는 Newton 방법과 같은 수치 해석적 방법보다 사용하기가 간편하다는 이점이 있다.

확률모형의 응용방법에 대한 또 다른 연구로 서순근과 조유희(2002)는 신뢰성 분석의 피로모형(fatigue)에서 설계곡선(design curve)을 설정하는 방법을 연구하였다. 이 논문에서는 기존 방법을 보완하는 기법으로 붓스트랩 기법을 적용하여 보다 일반화된 상황 하에서 설계곡선을 설정하는 방법이 제시되었고, 다수의 피로시험자료의 설계곡선을 설정하여 기존 방법과의 효율성을 비교 분석하는 연구가 수행되었다. 그리고 Nam, Kyung H. et al.(2006)은 재생과정(renewal process)의 재생함수(renewal function)을 추정하는 방법을 연구하였다. 이 논문에서 저자들은 재생함수 추정과정의 모형 중, Hjorth 모형과 Dhillon 모형의 재생함수를 근사적으로 추정하는 방법을 고찰하였으며 재생함수의 모수의 변화에 따른 재생함수의 추정 형태를 그래프로 제시하였다. 이 분야의 또 다른 연구로 황강진 외 2인(2002)은 혼합분포에서 새로운 자료가 연속적으로 생성되는 모형의 경우, EM 알고리즘을 적용할 때 혼합분포의 혼합비율을 새로이 추정함으로서 야기되는 과다한 수렴 반복 횟수를 줄이는 대안적 방법으로 동적 EM 알고리즘과 Titterintton 알고리즘 등을 고찰하고, 모의실험을 통해 두 알고리즘의 수렴정도를 비교하였다.

그리고 한성실 외 2인(2001)은 시스템이 주기마다 예방보전 활동이 이루어지고 각 주기마다의 예방보전에서는 새로운 시스템으로 교체되는 모형에서 주기적인 예방보전 정책에 대한 방법이 연구되었다. 이 논문에서 저자들은 고장률 함수가 와이불분포를 따를 때, 베이지안 관점에서 주기적인 예방보전 모형에 대한 단위시간 당 기대비용을 산출하는 방법과, 그에 따른 최적의 예방보전정책 설정방법 및 예방보전 방법들을 제시하였다. 그리고 오대호와 염준근(2002)은 복잡한 시스템들이 네트워크(network) 구조로 연결되어 있는 경우, 시스템들의 유효성을 평가하는데 있어서 시스템들의 신뢰도를 평가하는 방법을 고찰하였다. 이 연구에서는 Silvester가 제안한 MPS(most probable state)의 개념을 응용하여 각 시스템들의 신뢰도를 평가하는 방법들이 제시되었으며, 수치예제를 통하여 응용방법도 고찰되었다.

한편 확률모형을 응용하여 품질을 향상시킨 사례 연구로 류귀열(2014)은 확률분포를 이용한 포털들의 응답시간 품질에 대하여 고찰하였다. 이 연구에서 저자는 인터넷 포털들의 응답품질을 응답시간으로 설정하고, 연구 대상 사이트는 방문자 수 기준으로 상위 3대 포털 사이트인 Naver, Daum과 Nate를 선정하여, 확률모형을 이용하여 비교 연구하였다. 그리고 저자는 응답시간을 측정한 후, 분석방법으로는 평균비교를 위해서는 분산분석 그리고 응답시간 분포를 분석하는 데는 모수적 방법으로는 카이제곱 검정 및 비모수적 방법인 두 표본 콜모고로프-스미르노프 검정(two samples Kolmogorov-Smirnov test)을 실시하여 비교분석하였다. 그리고 위에서 고찰한 확률모형의 응용분야의 논문들을 시대 순으로 요약하면 <Figure 2>와 같다.

베이지안 분석기법을 응용한 연구 분야는 특히 앞에서 고찰한 확률모형 분야의 연구들과 상호연관성을 갖고 있다. 이 절에서 고찰할 확률모형에서 베이지안 기법을 적용한 연구들은 두 개의 세부 문야, 즉 중도 절단 모형 및 중도 절단되지 않은 모형에서 확률모형의 모수 및 확률을 베이지안 방법론을 적용하여 고찰하는 분야로 구분해 볼 수 있다.

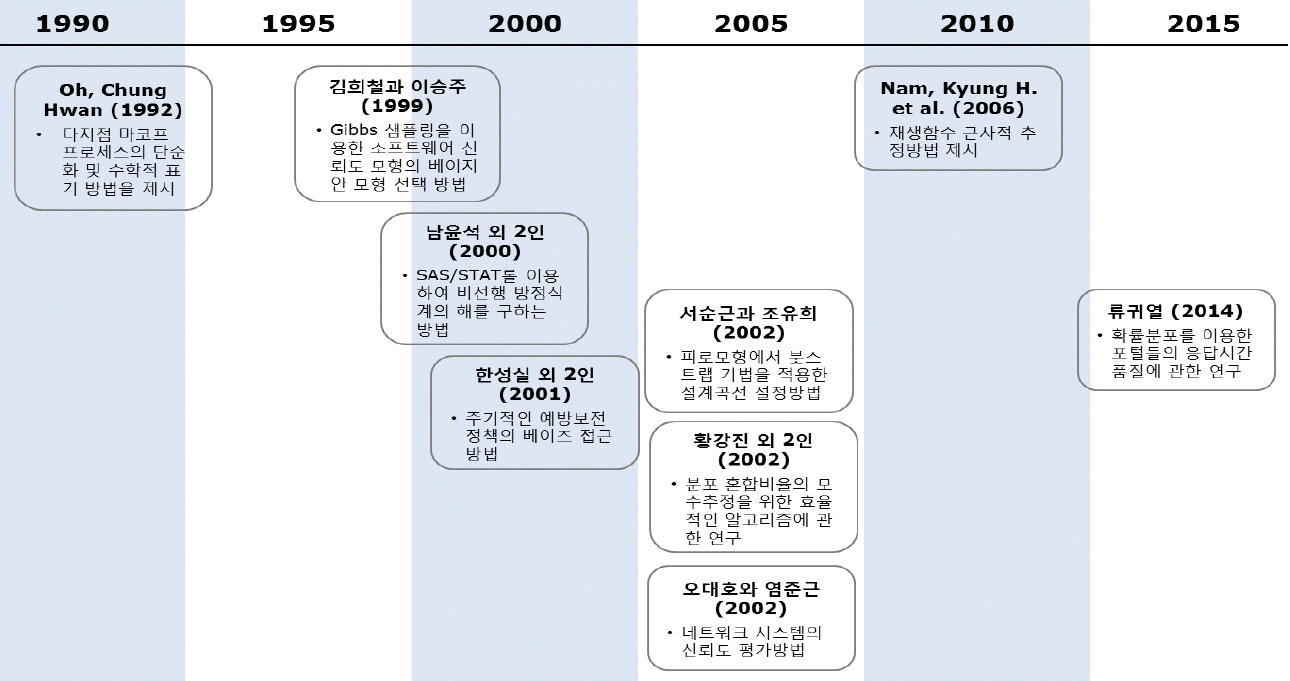
먼저 중도 절단된 모형에서 베이지안 방법을 적용한 연구로 Yeom, Joon Keun과 Kim, Jae Joo(1985)는 중도절단(censored)된 모형에서 어떤 확률변수가 다른 확률변수 보다 작을 확률에 대한 베이지안 추정 방법을 고찰하였다. 이 논문에서 저자들은 모든 아이템(item)들이 고장(사망)나기 전에 실험이 종료되는 경우와 고장이 난 아이템에 대해서는 부분적으로 교체하는 두 가지 경우에 대하여 추정 방법인 최우추정법, 최소분산불편추정법, 그리고 베이즈 추정법을 고찰하고 모의실험(simulation)을 통하여 여러 방법의 특징 및 효율성을 비교 분석하였다. 그리고 이 분야의 다른 연구로 Park, Man-Gon(1988)은 확률변수의 값의 영역이 특정 값 보다 크게 설정되는 좌측 절단된(left truncated) 지수분포 모형에서 모수추정방법을 연구하였다. 특히 저자는 이 연구에서 표본에 이상값이 포함되어 있는 경우 베이지안 추정방법과 이상값을 정상값으로 교체한 후의 추정 방법 등을 고찰하고, 모의실험을 통하여 각 방법들의 효율성을 비교 분석하였다. 더 나아가 Park, Man-Gon과 Jung, Yun-Sung(1989)은 좌측에서 중도 절단된 지수분포모형에서 시스템의 신뢰성을 베이지안 방법으로 추정하는 기법을 연구하였으며, 베이지안 추정량의 통계적 성질을 모의실험을 통하여 평균제곱오차의 관점에서 고찰하였다.

그리고 중도 절단되지 않은 확률모형에서 베이지안 기법을 응용한 추정방법에 대한 연구로 Kim, Jae Joo와 Park, Eun Sik(1990)은 이변량 지수분포 모형에서 어떤 확률변수가 다른 확률변수 보다 작을 확률에 대한 베이지안 추정방법의 효율성을 비교 분석하였다. 이 연구에서 저자들은 베이지안 추정량과 최우추정량의 효율성을 모의실험을 통하여 고찰하고, 베이지안 추정량이 최우추정량보다 우수할 뿐만 아니라, 여러 경우의 베이지안 추정량 중에서는 사전확률분포가 감마분포인 경우에 보다 우수한 추정방법이 된다는 것을 입증하였다. 또한 Kim, Jae Joo et al.(1994)은 Block 과 Basu의 이변량 지수모형에서 어떤 확률변수가 다른 확률변수 보다 클 확률에 대한 추정방법으로 적절한 사전분포와 이차손실함수, 가중된 이차손실함수를 가정한 경우의 베이지안 추정방법을 제시하고, 최우추정량 및 베이지안 추정량의 치우침(bias)와 평균제곱오차(MSE: mean squared error))를 평가하고 비교 연구하였다. 더 나아가 Kim, Jae Joo와 Park, Byung-Gu(1987)는 이변량 지수분포 모형에서 절단된 자료와 절단되지 않은 자료가 혼합되어 있는 경우의 모수추정방법을 고찰하였다. 이 논문에서 저자들은 최우추정법과 적률법 그리고 베이지안 추정방법에 의한 모수 추정방법들을 고찰하고, 각 추정방법의 효율성을 모의실험(simulation)을 통하여 비교분석하였다. 특히 이 연구에서는 저자들은 표본크기가 크기가 적당한 경우에 베이지안 추정방법이 다른 방법 보다 우수한 추정방법이 된다는 것을 입증하였다.

선형모형 분야에서 베이지안 방법을 적용한 논문으로는 Kim, Hea-Jung(1998), Kim, Hea-Jung과 Lee, Ae-Kyung(1998)의 연구가 있다. Kim, Hea-Jung(1998)에서는 회귀계수의 제약조건이 있는 다변량 회귀모형에서 깁스샘플러(Gibbs sampler)를 이용한 베이지안 추론방법이 고찰되었으며, 일반적인 회귀계수에 대한 베이지 방법의 사후분포를 계산하기 위한 방법으로, 일반적인 켤레사전분포(conjugate prior distribution)모형에서 깁스 샘플링(Gibbs sampling)를 이용한 베이지안 추론 방법이 제안되었고, 제시된 방법이 실제 문제에 적용되는 방법 등이 검토되었다. 그리고 Kim, Hea-Jung과 Lee, Ae-Kyung(1998)은 로지스틱 회귀모형에서 베이지안 방법을 응용하여 변수선택 기법을 연구하였으며, 종속변수가 이항분포를 따르는 변수인 경우 다수의 설명변수들 중에서 설명력이 있는 변수들만 선택하는 방법으로 깁스샘플링(Gibbs sampling)기법을 응용한 베이지안 분석 방법을 고찰하고 사례분석을 통하여 응용기법을 제시하였다.

기타 다른 통계적 방법론에서 베이지안 기법을 응용한 연구로는 염준근과 손창균(1995) 그리고 Kim, Hea-Jung과 Inada, K.(1995), Kim, Hea-Jung(2000) 및 김경숙과 손영숙(2002)의 연구가 있다. 염준근과 손창균(1995)은 Warner가 제안한 확률화 응답 모형에 대해 베이지안 추정방법을 고찰하였으며, O'Hagan의 이론을 2-단계 확률화 응답 모형에 적용하여 2-단계 확률화 응답 모형의 베이지안 추정방법을 제시하였다. 저자들은 이 연구에서 제시된 방법과 Mangat와 Singh가 제시한 2-단계 확률화 응답 모형의 추정량과의 효율성을 평균제곱오차(MSE) 관점에서 비교하였는데, 민감한 속성에 관한 조사에서는 제시된 베이지안 추정량의 평균제곱오차(mean squared error:MSE)가 작아져서 보다 효율적임을 입증하였다.

그리고 Kim, Hea-Jung과 Inada, K.(1995)는 다변량 분석 기법 중 판별분석에서 베이지안 방법을 응용하는 기법을 연구하였다. 이 연구에서 저자들은 주어진 다변량 자료를 다변량 정규분포를 따르는 두 개의 정규분포에 따르는 두 개의 집단으로 분류하는 경우, 사전확률분포가 알려져 있지 않은 경우의 베이지안 판별분류 방법을 제안하고 사례분석을 통하여 제시한 방법의 효율성을 고찰하였다. 특히 Kim, Hea-Jung(2000)은 선형 판별 분석에서 베이지안 관점에서 베이스 인자(base factor)를 사용하여 영향력 있는 관찰치를 검출하기 위한 새로운 진단 측도와, 이를 해석하기 위한 도구로서 시각적인 방법을 제시하고, 사례 분석을 통해 제안된 측도의 효율성을 고찰하였다. 그리고 김경숙과 손영숙(2002)은 베이지안 기법을 적용한 다중검정방법을 연구하였고, 이를 포아송 분포 모형의 평균 모수에 대한 다중 검정에 적용하는 방법을 실제 자료의 사례분석을 통해 제시하였으며 이론적인 결과를 검토하기 위해서 모의실험을 수행하여 제안한 방법의 장점 및 단점 등을 고찰하였다.

그리고 다른 연구로는 김희철과 이승주(1999)는 몬테칼로 깁스방법을 적용한 소프트웨어 신뢰도 성장모형에 대한 베이지안 추론과 모형선택 방법을 제안하였다. 이 연구에서는 Jelinski-Moranda 모형과 Goel-Okumoto모형 그리고 Schick-Wolverton모형에서 전통적인 최우추정법을 적용하여 모수를 추정하는 방법을 고찰하고, 위험함수의 형태와 초기오류수의 형태의 사전분포가 포아송분포인 경우 깁스샘플링법을 이용한 베이지안 추론과 상대오차의 합을 이용한 모형 선택 방법을 비교 분석하였다.

베이지안 분석 방법을 자료분석 분야에 응용한 연구로 김태규와 김명준(2015)은 베이지안 방법을 제품 품질관리 분야에 활용하는 방법을 고찰하였다. 이 논문에서 저자들은 일반 제조 과정에서 관리하고 있는 모수들에 대하여 이들의 분포를 일치시키는 추정방식인 제한된(constrained) 베이지안 추정 방식을 제시하였고, 산업 현장에서 활용되는 실제 자료를 바탕으로 기존에 널리 알려져 있는 베이지안 추정 방식과 제한된 베이지안 추정 방식을 비교하여 제한된 베이지안 방법에 의한 관리 방식이 보다 효율적임을 입증하였다. 특히 이 연구에서는 2014년 국내 타이어 제조업체 현장에서 관리하고 있는 주요 항목들의 표본을 추출하여 그 효용성에 대한 실증 분석을 실시한 점이 주목할 만한 점이다. 이와 같은 베이지안 분석분야의 논문들을 발표 시대별로 정리하면 <Figure 3>과 같다.

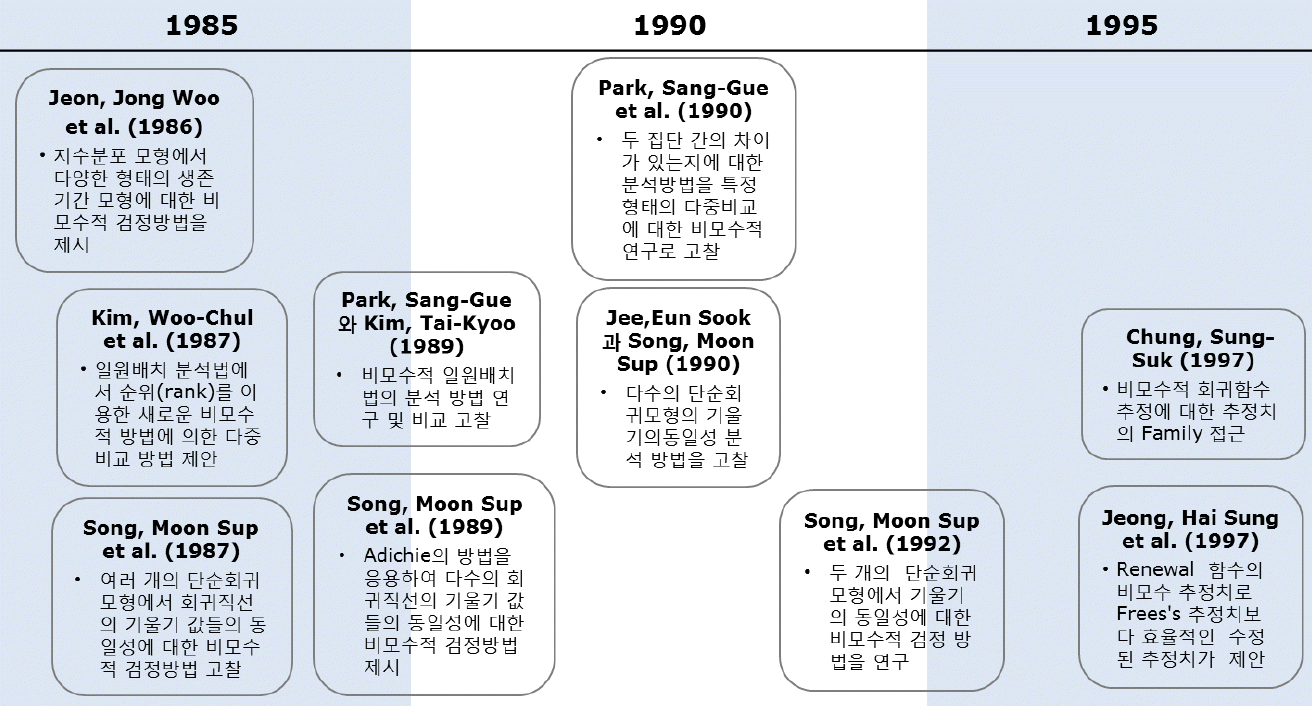
비모수적 방법의 연구 논문들은 실험계획분야, 회귀분석 분야 그리고 기타 통계분석 분야의 세 개의 세부 범주로 분류할 수 있었다. 먼저 실험계획분야의 연구로는 Kim, Woo-Chul et al.(1987)와 Park, Sang-Gue와 Kim, Tai-Kyoo(1989) 및 Park, Sang-Gue et al.(1990)의 연구가 있다.

Kim, Woo-Chul et al.(1987)은 일원배치 분석법에서 특정 형태의 다중비교(multiple comparison) 분석 방법을 연구하였다. 이 논문에서 저자들은 우도비 검정(likelihood ratio test)을 이용하여 특정 처리(treatment)가 다른 여러 개의 처리들 보다 우수한지를 검정하는 기존의 방법을 고찰하고 및 순위(rank)를 이용한 새로운 비모수적 방법을 제안하였으며, 기존의 실제 자료의 실증분석을 통한 비교분석을 통하여 제시한 방법의 효율성을 연구하였다. 그리고 Park, Sang-Gue와 Kim, Tai-Kyoo(1989)는 일원배치 분석법에서 표본자료의 순위(rank)를 이용한 비모수검정법을 연구하였다. 이 연구에서 저자들은 자료의 비선형순위(nonlinear rank)를 이용한 검정방법을 제안하였으며, Kruscal-Wallis 검정법을 비롯한 다수의 기존의 방법들과 저자들이 제시한 방법 간의 효율성을 모의실험을 통하여 고찰하였다.

한편 Park, Sang-Gue et al.(1990)의 연구는 특정 형태의 다중비교에 대한 비모수적 연구로 두 집단 간의 차이가 있는지에 대한 분석방법을 고찰한 논문이다. 이 논문에서 저자들은 하나의 집단은 제어(control)집단이고 다른 집단은 비교하고자 하는 집단인 처리집단인 경우, 두 집단 간의 효과의 차이에 대한 비모수적 신뢰구간을 추정하는 방법을 제시하고, 응용방법을 사례분석을 통하여 고찰하였다.

회귀분석 분야에서 비모수적 기법을 고찰한 연구를 살펴보면, 먼저 여러 개의 단순회귀모형에서 기울기의 동일성을 검정하는 방법을 고찰한 연구로 Jee, Eun Sook과 Song, Moon Sup(1990)이 있다. 이 논문에서는 설명변수들의 영역은 양수이고 동일한 절편을 갖는 여러 개의 단순회귀모형에서 비모수적 검정방법인 Jonckheere 방법을 연장하여 기울기의 동일성 검정에 대한 새로운 방법이 제시되었으며, 검정통계량의 점근분포(asymptotic distribution) 및 모의실험을 통한 여러 방법들의 효율성 등이 고찰되었다. 이와 연관성이 있는 또 다른 연구로 Song, Moon Sup et al.(1987)은 단순회귀분석에서 다수의 회귀직선의 기울기 값들이 동일한지에 대한 분석방법으로 비모적 검정방법을 고찰하였다. 이 논문에서 저자들은 여러 개의 단순회귀모형에서 기울기 값들이 동일한지 아니면 순위적으로(odered) 차이가 나는지에 대한 검정방법으로 Kepner와 Robinson의 방법을 응용하여 새로운 검정방법을 제시하고 모의실험을 통하여 검정방법의 통계적 효율성을 고찰하였다.

더 나아가 Song, Moon Sup et al.(1989)은 단순회귀분석에서 다수의 회귀직선의 기울기 값들이 동일한지에 대한 비모수적 검정방법으로 Adichie의 방법을 응용하여 새로운 검정방법을 제시하고 모의실험을 통하여 통계적 효율성을 비교 분석 하였다. 특히 또 다른 연구인 Song, Moon Sup et al.(1992)에서는 두 개의 단순회귀모형에서 기울기의 동일성 검정방법으로 1982년 Orban and Wolfe가 제시한 방법을 응용한 비모수적 검정방법이 제시되었고, 기존의 방법들과 제안한 방법 간의 효율성 등이 모의실험을 통해 연구되었다.

그리고 비모수 회귀분석(nonparametric regression)분야의 평활기법(smoothing)에 관한 연구로는 Chung, Sung-Suk(1997)의 연구가 있다. 이 논문에서 저자는 최적의 평활곡선(smoothing curve)의 후보로 하나의 곡선 추정곡선 대신 여러 개의 추정 곡선들의 집합인 군(family)을 고려하고, 최대 띠폭(bandwidth)의 한계치와 후보군(family) 구성원의 개수를 시뮬레이션을 통해서 제시하여 회귀선을 효율적으로 추정하는 방법을 제시하였다.

기타 다른 분야에서 비모수적 방법론을 고찰한 연구로 Jeon, Jong Woo et al.(1986)는 신뢰성 분석 및 생존분석 분야에서 많이 응용되는 지수분포 모형에서 다양한 형태의 생존기간 모형에 대한 비모수적 검정방법을 제시였다. 이 연구에서 저자들은 Kolmogorov-Smirnov 검정방법 및 Cramer-Von Mises 검정방법을 응용하여 새로운 형태의 검정방법을 제시하고, 검정통계량의 점근분포의 성질을 고찰하였다. 그리고 Jeong, Hai Sung et al.(1997)의 연구에서는 재생함수(renewal funtion)의 비모수적 추정치로 구간적 선형화에 근거한 Frees의 추정방법을 보완한 수정된 추정방법이 제시되었으며, 저자들은 모의실험을 통해 수정된 추정방법이 Frees의 방법보다 효율적임을 입증하였다. 그리고 이와 같은 비모수분석 분야의 논문들을 정리하면 <Figure 4>와 같다.

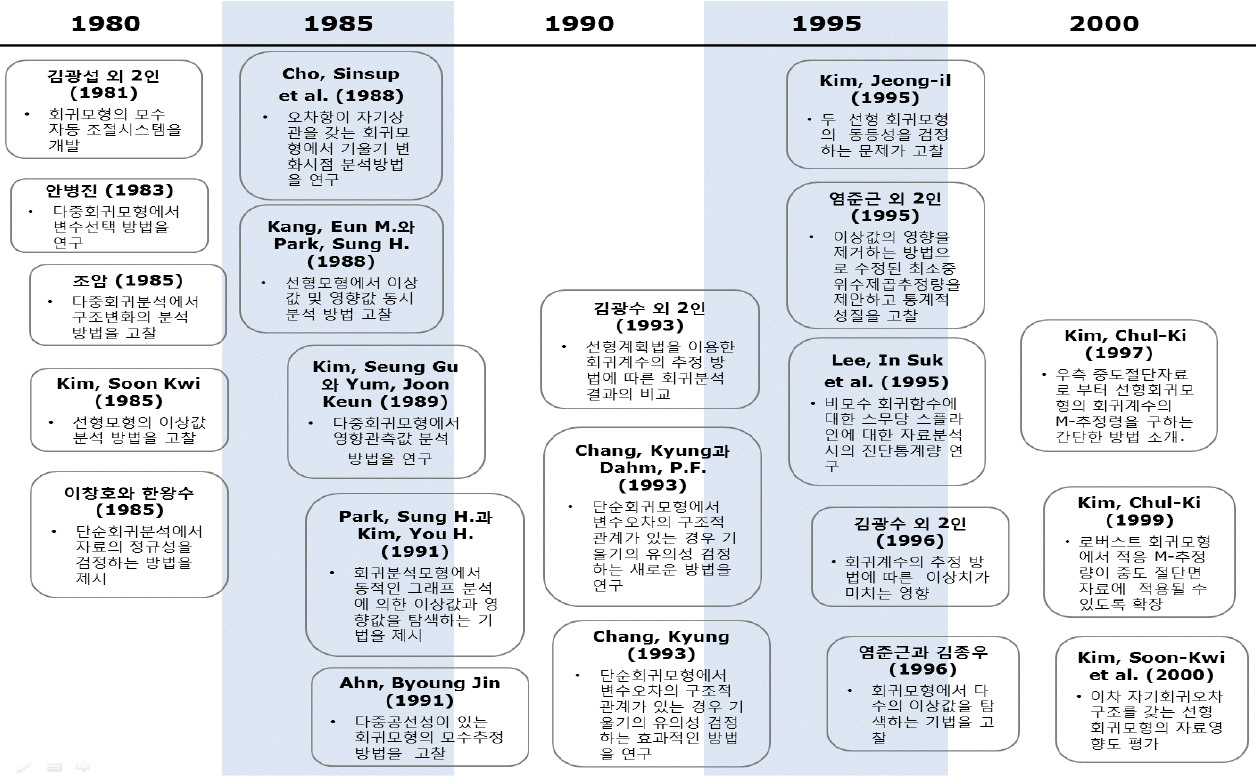
회귀분석분야의 연구는 회귀모형의 모수추정 방법과 이상값(outlier) 분석, 그리고 모형선택과 응용방법의 세가지 세부 범주로 분류할 수 있다. 먼저 회귀계수의 추정기법에 대한 연구로는 Ahn, Byoung Jin(1991), 김광수 외 2인(1993), Kim, Jeong-il(1995), 김광수 외 2인(1996) 및 Kim, Chul-Ki(1997, 1999) 등이 있다.

회귀계수에 대한 추정방법 연구로 Ahn, Byoung Jin(1991)은 다중공선성(multicollinearity)이 존재하는 다중회귀모형에서 효과적인 추정방법을 연구하였다. 이 논문에서 저자는 다중공선성에 영향을 주는 자료의 탐색 및 모수추정 방법으로 편의추정(biased estimation)방법인 능형회귀(ridge regression)방법을 응용하여 Mallow의 방법을 일반화한 통계량을 제안하였다. 그리고 김광수 외 2인(1993)은 다중 회귀분석에서 일반적인 회귀계수의 추정법인 오차의 제곱합을 최소화 하는 최소제곱법, 오차의 편차(absolute deviation)의 합을 최소화하는 방법과 오차의 최대편차를 최소화하는 방법을 상호 비교 고찰하고 모의실험과 사례분석을 통해서 예측의 정확성과 모형의 적합성을 비교 고찰하였다. 더 나아가 이 분야의 또 다른 연구로, 자료에 이상값(outlier)들이 포함되어 있는 경우 회귀계수의 추정방법인 최소제곱법, 절대편차합의 최소화 방법과 최대편차의 최소화인 방법을 적용했을 때, 각각 회귀계수 추정값들이 어떻게 이상치의 영향을 받는지를 고찰하고, 이상값 제거 전과 제거 후에 추정값들의 변화를 비교 고찰한 김광수 외 2인(1996)의 논문이 있다. 이 연구에서는 특히 정확성과 분산의 안정성 면에서 이상값을 제거하지 않은 상황에서 절대편차의 합을 최소화하는 추정방법을 추천하고 있다.

그리고 특별한 회귀모형의 모수추정 방법에 대한 연구로 Kim, Chul-Ki(1997)의 논문에서는 우측절단자료(right-censored data)를 이용하여 선형 회귀모형의 회귀계수의 M-추정량(M-estimators)를 계산하기 위한 비교적 간단한 방법이 소개되었다. 이 논문에서 저자는 제시한 방법은 절단되지 않은 완전한 데이터로부터 M-추정량을 계산하는 동일한 알고리즘을 반복적으로 결측 정보 원칙에 따라 재구성된 자료에 사용할 수 있으며. 이 방법에 의한 추정량은 순위(rank)를 이용한 추정량과 동일하게 이상값이나 영향값(influential data)에 영향을 크게 받지 않는 로버스트(robust)한 성질을 가지고 있고, 또한 계산의 간편성이 이점으로 작용하여 효율적인 방법임을 입증하였다. 더 나아가 Kim, Chul-Ki(1999)는 로버스트 회귀모형에 적용되는 M-추정량이 중도 절단된 자료에 적용될 수 있도록 확장한 새로운 추정방법을 제시하고, 제시된 방법이 다양한 오차들의 분포와 절단률에 대해서 다른 M-추정량 보다 우월함을 시뮬레이션을 통해서 보여 주었다.

특이 형태의 회귀모형에 대한 분석방법에 관한 연구로 조암(1985)은 다중회귀모형에서 설명변수들의 값의 영역에 따라 회귀직선이 달라지는 구조변화(structural change)가 존재하는 경우, 스플라인(spline) 기법을 이용한 회귀직선의 추정 방법을 고찰하였다. 이 논문에서 저자는 구조변화에 대한 사전 정보가 있는 경우와 없는 경우의 사후확률 (posterior probability)분포를 추정하는 방법과 사후확률을 이용한 베이지안 추정 방법에 의한 구조변화다중회귀 분석 방법을 연구하였다. 그리고 Cho, Sinsup et al.(1988)은 다중회귀모형에서 기울기 값들이 변하는 경우, 변화지점을 탐지하는 방법을 연구하였으며, 이 논문에서는 오차항이 1차 자기회귀모형으로 상호 결합되어있는 모형에서 베이지안 방법을 적용하여 오차항의 상관계수행렬을 알고 있는 경우 및 모르고 있는 경우 등, 다양한 경우의 분석 방법들이 제시되었다. 그리고 김광섭 등(1981)은 회귀모형의 모수 자동 조절시스템을 개발하였다. 특히 이 연구에서 저자들은 Durbin-Watson 통계량을 사용한 검정을 통하여 회귀계수 재조정의 시점을 탐지하는 기법과 함께, 회귀모형의 오차항에 대한 여러 기본 가정들이 만족되지 않을 때, 자동적으로 회귀계수를 조정하는 전산시스템을 개발하였고 사례분석을 통하여 적용기법 등을 제시하였다.

그리고 Kim, Jeong-il(1995)은 두 선형회귀모형의 동등성을 검정하는 문제를 고찰하였다. 이 논문에서 저자는 기존의 Chow 검정방법의 문제점을 검토하고, 우도비 검정, F-검정 및 Chow의 검정법의 상호 연관성을 고찰한 후, 두 선형회귀모형의 동등성을 검정하는 통계량으로 Score 검정통계량을 제안하고, 제시한 Score 검정방법이 점근적으로 Chow 검정과 우도비 검정과 일치함을 입증하였다. 다른 연구로 Kim, Soon-Kwi et al.(2000)는 오차항이 2차의 자기회귀모형(autoregressive model)인 일반선형회귀모형에서 모든 모수들에 대한 반응치 벡터의 동시 흔들림의 영향을 고찰하여, 이에 대한 진단 통계량을 제시하였을 뿐만 아니라 국소 영향력에 대한 최대의 곡률을 검출하는 방법들을 다양하게 제안하였다.

이상값(outlier) 및 영향값(influential data)을 분석하는 연구로는 Kim, Soon Kwi(1985) 그리고 Kang, Eun M.와 Park, Sung H.(1988), Kim, Seung Gu와 Yum, Joon Keun(1989), Park, Sung H.과 Kim, You H.(1991), 염준근 외 2인(1995) 및 염준근과 김종우(1996)의 연구가 있다. 먼저 Kim, Soon Kwi(1985)는 선형모형에서 잔차(residual)를 이용하여 이상값(outlier) 분석방법을 고찰하여, 이상값 판단 통계량으로 수정된 표준화 잔차의 최대값( maximum modified normed residual)의 산출방법과, 제안한 통계량의 확률분포를 연구하여 이상값으로 판단할 수 있는 임계값 및 이상값 식별방법을 제시하였다.

그리고 Kang, Eun M.와 Park, Sung H.(1988)은 선형모형에서 이상값(outlier) 및 영향값을 탐지하는 방법으로, 이상값을 탐지하는데 사용되는 통계량과 영향값을 분석하는데 사용할 수 있는 통계량을 결합하여 새로운 검정통계량 및 검정방법을 제시하였으며, 모의실험을 통하여 단순회귀분석에 적용하는 경우 제시한 통계량의 임계값 결정방법을 고찰하였다. 이와 관련된 연구로 Kim, Seung Gu와 Yum, Joon Keun(1989)은 다중회귀모형에서 영향값을 판단하는 방법을 연구하였다. 이 논문에서 저자들은 기존의 방법인 햇-행렬(Hat-Matrix)의 대각항을 이용하는 방법과 함께 비대각항을 함께 고려하는 방법을 제안하고 있으며, 실증사례 분석을 통하여 제안한 방법의 효율성을 입증하였다.

그리고 Park, Sung H.과 Kim, You H.(1991)는 회귀분석모형에서 그래프를 이용한 이상값 분석 방법을 고찰하였으며, Cook과 Weisberg의 그래프 분석방법을 응용하여 동적(dynamic)인 그래프 분석에 의한 이상값과 영향값을 탐색하는 기법을 제시하였다. 이상값 분석에 대한 또 다른 연구로 염준근 외 2인(1995)은 이상값의 영향을 제거하는 방법으로 잔차 제곱값의 중위수를 사용하는 최소중위수제곱(least median square)추정량의 방법을 수정하여 새로운 분석방법과 통계적 성질을 고찰하였고, 염준근과 김종우(1996)는 회귀모형에서 다수의 이상값을 탐색하는 기법을 고찰하였다. 이 논문에서는 이상값이 없는 집단인 clean 집단과 이상값이 존재할 수 있는 remained 집단으로 구분하는 방법과 함께, clean 집단을 사용하여 remained 집단에 속해있는 이상값을 순차적으로 식별하는 외향성 방법(outward procedure)이 제시되었다.

회귀분석에서 모형선택 및 일반적인 가정이 성립되지 않는 경우의 분석 방법에 대한 연구로 안병진(1983), 이창호와 한왕수(1985) 및 Chang, Kyung과 Dahm,P. F.(1993), 그리고 Chang, Kyung(1993)의 연구가 있다. 안병진(1983)은 다중회귀모형에서 여러 개의 독립변수들 중에서 설명력이 유의한 변수들만을 선별하는 변수선택(variable selection)방법을 고찰하였으며, 변수선택 기준으로 누적분산(integrated variance)과 누적편의제곱(integrated squared bias)의 비율값을 가중값으로 사용하는 새로운 방법을 제시하고, 실제 자료의 사례분석을 통해 응용방법을 고찰하였다. 특히 이창호와 한왕수(1985)는 단순회귀분석에서 자료가 정규분포에 따르는지를 검정하는 방법을 제시하였다. 이 논문에서 저자들은 표본평균과 표본분산이 확률적 독립성을 갖는 일반적인 상황에서 종속변수가 정규분포에 따르는지를 검정하는 방법을 제시하고 모의실험을 통하여 종속변수가 정규분포이외의 다양한 분포에 따르는 경우 기존 검정방법과의 통계적 효율성을 연구하였다.

그리고 종속변수뿐만 아니라 독립변수들도 확률변수의 성격을 갖는 변수오차(measurement error)문제에 대한 연구로는 Chang, Kyung과 Dahm, P. F.(1993), Chang, Kyung(1993)의 연구가 있다. 먼저 Chang, Kyung과 Dahm,P. F.(1993)은 단순회귀모형에서 변수오차(measurement error)의 구조적 관계(structural relationship)가 있는 경우 기울기의 유의성 검정하는 새로운 방법을 연구하고, 모의실험을 통한 제시한 검정방법의 통계적 효율성 및 검정통계량의 점근분포에 대하여 고찰하였다. 그리고 더 나아가 Chang, Kyung(1993)은 단순회귀모형에서 변수오차(measurement error)의 구조적 관계(structural relationship)가 있는 경우 기울기의 유의성 검정 방법에 연구로, 기존의 저자가 제시한 기존 논문의 방법을 수정하여 새롭게 근사적인 방법을 제시하고 있으며. 제시한 방법이 기존의 방법보다 효과적인 기법임을 입증하였다. 그리고 Lee, In Suk et al.(1995)은 비모수 회귀곡선 추정방법에 관한 연구로, 평활기법인 스무딩 스플라인(smoothing spline)에 기법을 적용하여 자료를 분석할 때 사용될 수 있는 진단통계량을 연구한 논문으로, 이 연구에서는 기존의 통계량을 수정하여 일반화된 검정통계량과 통계량의 통계적 성질이 고찰되었다. 그리고 <Figure 5>는 이와 같은 회귀분석 분야의 논문들을 그림으로 요약하여 보여주고 있다.

시계열 분석 기법과 예측 기법에 대한 연구로는 조엄(1986), Ryu, Gui Yeol et al.(1989), 김혜중과 이애경(2001), Lim, Seongsik et al.(1996) 그리고 김홍민과 정병희(2008)의 연구가 있다. 먼저 시계열 분석 분야의 연구로 Ryu, Gui Yeol et al.(1989)은 자기회귀모형인 AR(1)모형에서 모형의 변화시점을 판단하는 방법을 고찰하였다. 저자들은 베이지안 방법을 적용하여 모형의 계수의 변화시점 혹은 분산이 변하는 시점, 또는 계수와 분산이 모두 변화하는 시점을 판단하는 통계적 방법론을 제시하였으며, 컴퓨터로 생성된 모의자료 분석은 통하여 제안한 방법의 응용기법을 고찰하였다. 그리고 Lim, Seongsik et al.(1996)에서는 표본 크기가 작은 표본에서 뿐만 아니라 모수가 시간에 따라서 변하는 경우에도 유용한 공간 시계열 모형이 제안되었고, 모형식별(identification), 모수추정(estimation)과 모형진단(diagnostic checking) 이라는 3 단계 분석 절차와 함께 실제 자료의 사례분석을 통하여 적용방법을 제시하였다.

예측기법 분야의 연구로 조엄(1986)은 Ivakhnenko가 예측기법으로 제안한 집단적 방법(grouping method of data handling: GMDH)의 효율성을 연구하였다. 이 논문에서는 다양한 자료 모형의 분석 및 예측 방법으로 GMDH 방법과 다중회귀방법 및 지수평활방법간의 효율성을 모의실험(simulation)을 통하여 비교 분석하여 자료의 크기의 변화에 따른 각 방법의 특징 등이 비교 검토되었다. 한편 김헤중과 이애경(2001)은 Laplace-Metropolis 알고리즘을 사용하여 다항로짓모형의 주변우도 함수를 근사적인 방법으로 추정하는 절차를 고찰하고, 추정된 주변 우도함수를 변수 선택 기준으로 삼아 베이지안 접근법에 의한 다항로짓모형의 변수선택 기준 및 최적의 변수 선택 방법과 예측응용 기법을 제안하였다. 또한 이 논문에서는 모의실험을 통해서 제안된 변수 선택법의 유용성이 평가되었다. 그리고 김홍민과 정병희(2008)는 전통적인 수요예측모형이 갖는 한계성을 보완하는 방법으로 벡터오차수정모형(vector error correction model)을 통한 희유금속의 수요모형을 구축하고, 적용사례로 국내 희귀금속의 수요예측모형을 고찰하였다. 이 연구에서 저자들은 희유금속 중 대표성을 갖는 금속으로 크롬을 선택하였으며, 크롬의 수요예측에 영향을 주는 변수로 크롬의 가격과 국내총생산(GDP) 및 산업생산지수를 도입하여 합당한 수요함수를 설정하고, 시계열의 안정성과 변수간의 장·단기적 균형관계를 고려하여 벡터오차수정모형을 구축하였다. 이러한 시계열 분석 기법과 예측 기법에 대한 연구들을 그림으로 정리하면 <Figure 6>과 같다.

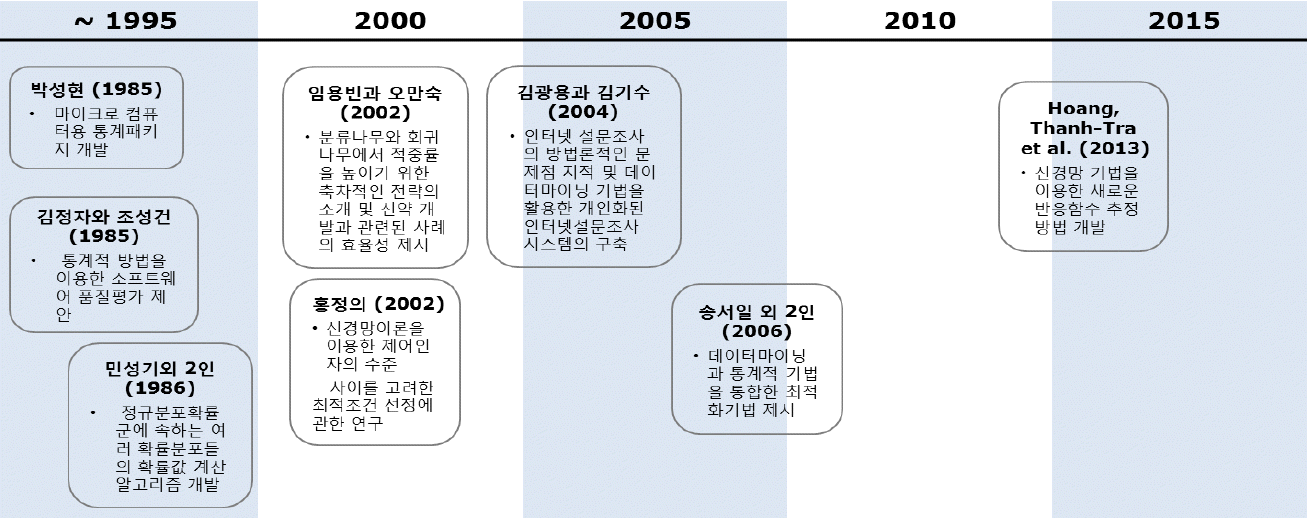
자료분석 분야의 응용논문들은 데이터마이닝 및 신경망기법을 고찰한 범주와, 통계적 분석 방법에 대한 컴퓨터 패키지 개발 및 그와 연관된 연구논문 및, 기타 다양한 통계분석 기법을 적용하여 사례 등을 분석 연구한 세 가지 세부 범주로 구분 할 수 있다. 먼저 데이터마이닝 및 신경망 기법 범주의 연구논문들은 2000년대 초반에 집중적으로 발표되었으며, 이에 해당하는 연구들로는 임용빈과 오만숙(2002), 홍정의(2002), 김광용과 김기수(2004), 송서일 외 2인(2006) 및 Hoang et al.(2013)이 있다.

임용빈과 오만숙(2002)은 대용량 자료를 다루는 데이터 마이닝에서 분류나무와 회귀나무의 불안정성을 개선하고 예측치의 정밀성을 높이기 위한 해결책의 하나로 다중나무 예측방법에 대한 알고리즘을 소개하였다. 이 연구에서 저자들은 항암제나 에이즈 치료를 위한 백신개발 등의 연구 개발의 처음 단계에서 소규모 양의 합성과 검사로 얻어진 자료를 분석하는 방법으로, 회귀나무를 이용하여 반응치를 예측하여, 합성되지 않은 수십만 개의 화합물들 중에서 효능이 있으리라 기대되는 화합물들을 선별하는 과정을 반복하는 축차적인 전략을 제시하였다. 그리고 홍정의(2002)는 신경망이론을 이용한 제어인자의 수준사이를 고려한 최적조건 선정에 관한 연구를 행하였다. 이 연구에서는 다구찌(Taguchi) 방법의 단점을 보완하는 방법으로 인공지능의 추론 기능을 이용하여 최적조건을 결정하는 방법을 제시하였다. 특히 이 논문에서는 일반적인 분석방법인 실험계획법상의 수준간의 최적 조건을 찾는 방법과는 달리 수준내의 최적조건을 선정 할 때 신경망이론을 사용할 수 있음을 보여주고 있다.

김광용과 김기수(2004)는 전통적인 설문방식에서 응답의 질을 통제했던 면접조사자(interviewer)의 역할을 인터넷 설문조사에서 사례기반추론이라는 데이터마이닝 기법으로 대체하여, 기존 고객의 인지적 정보를 수집하는 기법을 제안하였다. 이 논문에서는 제시한 방법이 기존의 오프라인 설문방식보다 웹 기반의 상호작용성과 멀티미디어적 장점을 최대한 활용하여 더욱 친근한 인터페이스를 구현함으로써 무응답 오류와 측정 오류를 줄여 설문 품질을 높이는 한편 데이터마이닝 기법을 활용한 개인화된 인터넷설문조사 시스템의 구축방법이 제시되었다.

그리고 송서일 외 2인(2006)은 데이터의 양이 방대하고 많은 인자를 포함하는 제조환경 때문에 발생하는 기존의 통계적 기법의 한계를 극복하기 위한 하나의 방안으로서 데이터마이닝 기법과 통계적 기법을 통합하여 보다 실용적이고 효율적인 최적공정설계 기법을 개발하였다. 이와 관련된 또 다른 연구로 Hoang et al.(2013)은 신경망 기법을 이용한 새로운 강건(robust) 반응함수 추정 방법을 고찰하였고 이 방법이 반응표면분석의 대안으로서 쓰일 수 있음을 밝혔다. 저자들은 이 연구에서 고찰한 네 가지 강건계획(robust design) 모델들을 대상으로 추정 및 최적화 측면에서 반응표면분석에서 일반적으로 사용하는 최소제곱추정법보다 새로운 신경망기반을 적용한 추정방법이 예측품질손실함수 값으로 평가할 때 보다 효율적인 방법임을 모의실험을 통해 입증하였다.

통계적 분석 방법을 프로그램화 화는 컴퓨터 패키지 개발 및 그와 연관된 연구로는 박성현(1985), 김정자와 조성건(1985), 민성기 외 2인(1986)의 연구가 있다. 먼저 박성현(1985)은 마이크로 컴퓨터에 의한 통계자료분석 컴퓨터 프로그램인 대화식 통계패키지 ‘SQC’를 개발하였다. 이 패키지에 포함되어 있은 통계분석 기법들은 ‘각종 통계그래프’, ‘일표본 및 이표본 추정 및 검정’, ‘적합도 검정’, ‘난수(random number) 발생기’, '회귀분석 및 상관분석', '반응표면분석', '실험계획법', '관리도' 등이다. 그리고 김정자와 조성건(1985)은 통계적 방법을 이용한 소프트웨어 품질평가를 제안하였다. 저자들은 소프트웨어 개발 시 발생되는 요인들을 변수로 하여 통계적 방법을 이용하여 소프트웨어 개발 단계에서 발생될 수 있는 각 종 요인들과 최종 제품과의 상관관계를 분석하여 소프트웨어 개발 시 적용이 가능한 방법을 제시하였다. 그리고 민성기 외 2인(1986)은 마이크로 컴퓨터를 이용하여 정규분포확률 군에 속하는 여러 확률분포의 확률값 계산 알고리듬을 연구하였으며, 기존의 다양한 계산방법들의 효율성과 정확성을 컴퓨터의 C.P.U 시간과 근사값의 정확도 관점에서 비교 고찰하여 Zelen 과 Severo의 방법이 보다 효과적인 확률계산방법임을 입증하였다. 이와 같은 논문들을 정리하면 <Figure 7>과 같다.

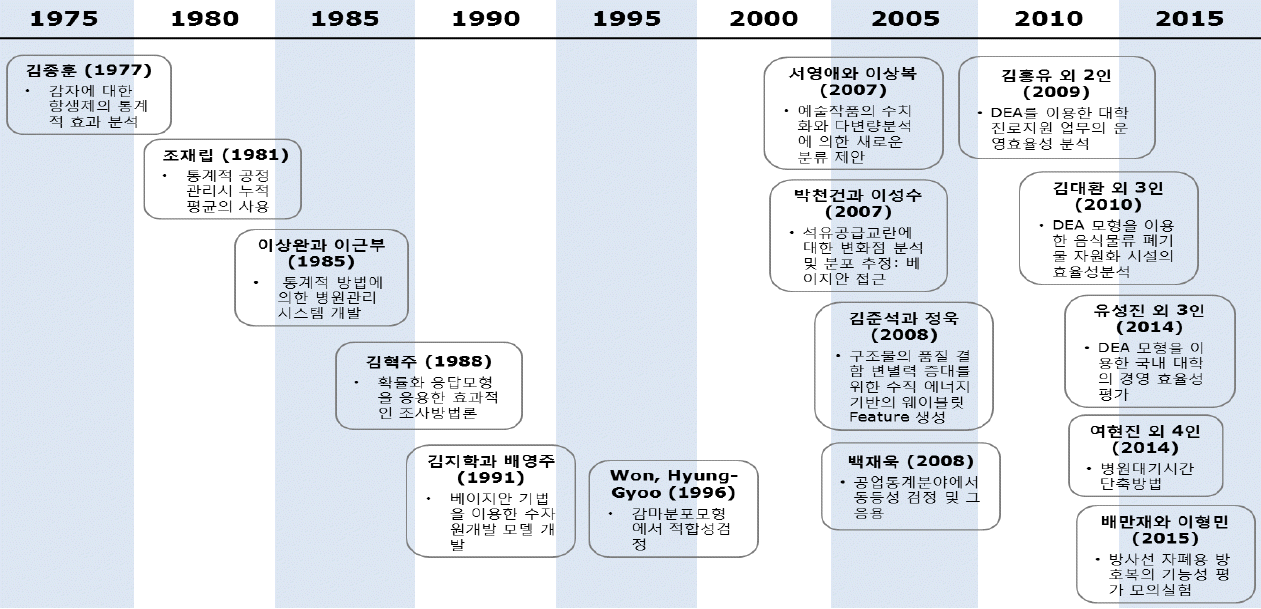
다음으로 자료분석 기법의 적용방법을 연구한 범주의 논문으로는 조재립(1981), 김혁주(1988), Won, Hyung-Gyoo(1996), 백재욱(2008)의 연구가 있다. 조재립(1981)은 통계적 공정관리를 분석하는 과정에서 전통적인 누적합(cummulative sum)을 이용하여 분석하는 방법대신 누적평균(cummulative mean)을 사용하는 것이 보다 효과적인 방법이 되는 경우를 고찰하였다. 이 논문에서 저자는 누적평균의 통계적 성질을 고찰하고 공정의 경향변동(trend variation)을 파악하고자 하는 경우 누적평균을 사용하는 것이 보다 효과적임을 제시하였다. 김혁주(1988)의 연구에서는 면접을 이용한 표본조사방법에서 효과적인 조사방법론이 고찰되었으며, 이 연구에서 저자는 Warner가 제시한 확률화 응답모형(randomized response model)을 응용하여 새로운 조사방법을 제시하고 기존방법과의 효율성을 비교 고찰하였다. 그리고 Won, Hyung-Gyoo(1996)에서는 감마분포 모형에서 적합성(goodness of fit) 검정방법이 고찰되었다, 이 연구에서 저자는 모집단의 분포가 모수 값들이 알려져 있지 않은 감모분포에 따르는 경우, Anderson과 Darling의 검정방법을 응용하여 표본자료가 감마분포에 적합한지를 검정할 수 있는 새로운 방법을 제시하고 모의실험을 통하여 제시한 방법의 효율성을 고찰하였다. 그리고 백재욱(2008)은 두 모집단간의 평균의 동등성(equivalence)을 검정하는 방법을 고찰하였다. 이 논문에서 저자는 기존의 두 표본 t-검정법의 문제점과 이를 보완한 두 모집단간의 평균 동등성 검정법의 적용 방법을 고찰하고 실제 산업현장에서 t-검정법과 동등성 검정법의 적용 방법 등을 실제 사례분석 통하여 비교 제시하였다.

품질경영분야의 사례분석을 통해 품질 혁신 방법을 고찰한 범주의 논문으로 김중훈(1977)은 감자에 대한 항생제 피마리신의 효과에 관한 연구 분석으로, 각 처방별로 피마리신의 처리효과를 비교한 분산분석 결과와 함께, 항생제 효과 조사 실험의 결과를 해석하였다. 그리고 이상완과 이근부(1985)는 통계적 방법에 의한 병원관리 시스템을 개발하였다. 저자들은 이 연구를 통해 의료업무 분석, 환자동향 분석, 의사-환자 간 상관분석, 주간별 진찰 회전율 분석, 불안정한 진료 분야의 진찰 회전율 동향분석을 통하여 종합병원 진료대기시간 연장 및 의료기관의 업무량의 증가에 따르는 문제점을 분석하고 개선책을 제시하였다. 한편 김지학과 배영주(1991)는 베이지안 기법을 응용하여 수자원개발 모델을 개발하였다. 저자들은 수자원개발 과정을 모형화 하는 데 있어서의 불확실성을 베이지안 방법을 적용하여 기회손실의 기대값을 산출하는 방법과 그에 따른 최적대안을 제시하고 베이지안 수자원개발 모델을 사례에 적용하여 산업현장에서의 응용기법을 제시하였다.

그리고 서명애와 이상복(2007)은 예술작품에 대한 수치화와 다변량 분석에 의한 새로운 분류 방법을 제안하였다. 저자들은 예술품 해석과 관련하여 미의 형식, 주관성, 객관성, 상징성, 미적 정보, 의미 정보와 같은 6개의 범주를 선정한 후, 감상자들이 예술작품을 평가한 평가결과 자료를 사용하여 다변량 통계기법인 집락분석을 응용하여 새로운 분류 기법을 제안하였다. 박천건과 이성수(2007)는 석유공급교란에 대한 변화점 분석 및 분포추정을 베이지안 접근 방식으로 분석하는 사례를 연구하였다. 저자들은 석유비축모형의 핵심인 석유공급교란의 형태를 파악하기 위하여 와이블분포를 사용할 때 변화점 추정 및 그 시점을 기준으로 분리된 와이블 분포들을 베이지안 방법으로 추정하는 기법을 제시하였다.

또 다른 사례연구로 김준석과 정욱(2008)은 구조물의 품질 결함 변별력 증대를 위한 수직 에너지 기반의 웨이블릿 요소(feature) 생성 방법을 고찰하여, 진동기반의 결함·탐지 기법 사용 시 분석대상인 변수의 수를 줄이고 모우드 속성 변화에 민감한 요소(feature)들을 찾아내는 방법을 제시하였다. 이 요소(feature) 생성 방법은 결함 여부의 탐지 및 정상 혹은 비정상 군집들의 효과적인 가시화를 위하여 군집 간 변별력이 우수한 소수의 웨이블릿 계수들을 생성하는 기법이라고 할 수 있다.

특히 이 사례분석 분야에서는 자료포락분석(data envelopment analysis: DEA)기법을 응용한 사례분석 연구가 주목할 만하다. 김흥유 외 2인(2009)은 DEA를 이용한 대학 진로지원 업무의 운용효율성에 대하여 고찰하였다. 이 연구에서 저자들은 서울소재 4년제 대학의 취업률과 제반 교육시설여건 등의 관련 자료를 조사한 후 자료포락분석 기법을 응용하여, 각 대학별로 취업의 운영효율성 실태를 고찰하고 이를 바탕으로 올바른 취업 및 진로지원 체계에 대하여 연구하였다. 이 연구의 DEA 모형에서는 투입요소로서 교지확보율, 직원수, 교사시설확보율, 산출요소로서 정규직 취업률, 취업률을 선정하였다. 그리고 김대환 외 3인(2010)은 DEA 모형을 이용한 음식물류 폐기물 자원화 시설의 효율성분석을 제시하였다. 이 연구에서 저자들은 전국 41개 민간부분 음식물류 폐기물 자원화 시설을 대상으로 DEA 모형을 이용한 효율성 분석을 시도하였으며, DEA 모형 분석 시 투입요소로서 자본금과 시설용량, 산출요소로서 매출액과 처리량을 선정하여 분석하였다.

그리고 유성진 외 3인(2014)은 DEA 모형을 이용한 국내대학의 경영효율성 평가에 대한 고찰을 하였다. 저자들은 DEA를 활용한 우리나라 대학의 경영 효율성 측정 결과와 붓스트랩 기법을 적용하여 편차가 제거된 효율성 결과를 함께 제시하고, 붓스트랩 방법을 통해 효율성 측정치의 통계적 유의성 검증을 시도하였다. 이 연구에서 저자들은 절단회귀모형으로 알려진 토빗모형을 사용하여 제시된 효율성 점수를 종속변수로 하고 효율성에 영향을 미치는 원인변수를 확인하고 기존 선행연구를 참조하여 제시된 교육 및 연구 모형과의 상관관계를 고찰하였다. 이를 통하여 저자들은 한국의 국·공립대 및 사립대의 경영 효율성을 평가하고 그것에 영향을 미치는 원인을 비교 분석함으로써, 한국 대학의 경영 효율성에 영향을 끼치는 요소에는 어떠한 것들이 있는지에 대한 탐색과, 현재 한국 대학들이 대학의 자원을 어느 분야에 더욱 집중하고 있는지를 분석하였다.

이 분야의 또 다른 사례 연구로 병원에서 환자들이 진료가 종료되는 시점까지 대기시간을 단축하는 방법을 고찰한 여현진 외 4인(2014)의 연구가 있다. 이 논문에서는 관심 있는 특정 진료 프로세스에 대해 연구된 기존의 방법과는 달리 여러 프로세스가 연속적으로 진행되는 경우 대기행렬모형과 의시결정나무분석기법을 응용하여 전체 대기시간을 단축하는 주요요소를 분석하고, 개선전략을 제시하였다. 그리고 배만재와 이형민(2015)은 방사선 물질이 방출되는 환경에서 사용되는 방호복 소재 개발 과정에서의 모의실험 응용기법을 고찰하였다. 이 논문에서는 장소, 시설 등의 다양한 환경조건이 차이에 따라 모의실험 환경을 설정하는 방법과 그에 따른 방사선 자폐용 방호복의 기능성을 평가하는 모의실험 설계 방법 및 자료 분석 기법 등이 제시되었다. 그리고 이러한 자료 분석 기법 분야의 연구들을 정리하면 <Figure 8>과 같다.