기동/화력 장비 신뢰도 성장모형 적용 사례
Abstract
Purpose
In this study, A reliability assurance model (or reliability program) is proposed to evaluate the reliability of an armed vehicle. The reliability assurance is performed through the reliability-centered activities in the K-000(armed vehicle) of D-Company
Methods
By reflecting the current situations of korea defense industry, a reliability assurance model is built up based on the benchmarking results of world leading companies’ best practices in same fields. So The reliability growth model is applied the Crow-AMSAA model
Results
This research analysis the K-000(armed vehicle) of D-Company using the DT and OT failure data. and application case study by growth model of armed vehicles
Conclusion
This research is result of application case study by growth model of armed vehicles
Key words: FRACAS, Growth Model, Crow-AMSAA
1. 서 론
1.1 연구의 배경
현재 우리나라 기업에서 생산하고 있는 체계 장비 신뢰성 관련 기술(설계, 평가, 시험, 분석 및 생산 기술)은 장비의 중요성에 비해 상당 부분 미흡하거나, 비효율적으로 운용되어 오고 있는 것이 사실이다. 무기체계의 고장으로 인하여 임무를 달성하지 못하거나 요구한 성능을 발휘하지 못하는 경우 막대한 손실을 초래하게 된다. 하지만, 무기체계에 요구되는 성능의 다양화와 기능의 복잡성 때문에 기술의 진보에도 불구하고 임무를 달성하지 못하거나 그 성능을 제대로 발휘하지 못하고 있으며 신뢰도의 문제를 여전히 가지고 있다. 일반적으로 무기체계에서는 설계 단계의 고유 신뢰도 값과 실제 야전에서의 운용 신뢰도 값 사이에는 큰 차이가 있는 경우가 많다. 이 연구에서는 이러한 부분을 조금이나 개선하고자 신뢰도 성장 모형 적용을 제안하고, 사례를 다루었다. 여기서, 신뢰도 성장 모형은 여러가지 모형 중 Crow-AMSAA 모형을 의미하며, 신뢰성 성장모형을 적용하기 위해서는 체계 또는 시스템에 대하여 신뢰성 시험을 실시하고, 고장 정보를 수집 및 근본원인을 분석하여 설계, 재질 등에 피드백하여 시정조치를 취하는 일련의 과정이 이루어져야 한다.
1.2 연구 목적 및 범위
이 연구는 기동장비의 운용 신뢰도 목표 값 달성을 위한 방안의 일부인 중 신뢰도 성장(Reliability Growth) 모형의 적용 사례를 Case Study로 제안한 논문이다. 구체적으로 기동 장비의 획득 단계 중 양산 단계의 진입 시점을 기점으로 하여 개발시험(Development Test) 및 운용시험(Operation Test)평가 단계에서 신뢰도 성장모형을 적용한 사례이다. 적용 장비는 D사에서 개발 완료한 K-000(장갑차)이다.
2. 기동장비 신뢰도 성장 방안
2.1 신뢰도 성장 모형
기동장비/무기체계에 대하여 고객이 요구한 목표 신뢰도를 달성하기 위해서는 신뢰성 시험을 실시하여 고장정보를 수집하고, 고장에 대한 근본원인을 파악 및 분석하여 시정조치 (Corrective Action)를 취하는 일련의 프로세스를 반복적으로 수행하여야 한다. 또한, 초기 계획한 신뢰도(Planned Reliability)를 달성하지 못하였다면, 달성을 위한 자원(예산, 시험기간, 시제 수 등)을 수정 반영하여 신뢰성 시험을 실시하며, < Figure 1>과 같은 프로세스를 가진다. 반복적인 프로세스의 결과로 무기체계의 신뢰성이 시간에 따라 향상되는 것을 신뢰도 성장(Reliability Growth) 이라고 하며, 이를 수학적 모형으로 나타낸 것을 신뢰도 성장 모형(Reliability Growth Model) 이라 한다. 신뢰도 성장 모형 중 대표적인 모형은 Duane 모형과 Crow-AMSAA 모형이 있다. 이 논문에서는 Crow-AMSAA 모형만을 다룬다.
2.1.1 Crow-AMSAA 모형
Crow-AMSAA 모형은 Crow(1974)가 Duane의 모형(1974)에서 비동질적 포아송 프로세스(NHPP)의 개념을 추가한 것으로, 확률적으로 설명한 모형이다. 시간 t에서 고장 강도 함수 p( t)를 식 (1)과 같이 2개의 모수를 가지는 와이블 고장률 함수로 근사시켜 나타낼 수 있다. 여기서, β는 형상모수, λ는 척도모수이다. 따라서, 총 시험기간 [0, T]에서의 기대고장개수를 E[ N( T)]라 할 때, 식 (2)와 같다. 또한, 순간 평균 고장 시간 (Instantaneous MTBF)를 m( T)라고 하면 식 (3)과 같다.
2.1.2 Crow-AMSAA 모형의 모수 추정
시험시간 Ti-1시점에 ( i-1) th의 고장이 발생했을 때, Ti시점에 ith의 고장에 대한 확률밀도함수는 식 (4)와 같이 나타낼 수 있다. ( i=1,2,⋯, n) 여기서, 우도함수를 구하면 식 (5)와 같다. 단, T*는 시험 종료 시간이다. 시험이 n번째 고장에서 중단되면 T*는 T*= Tn이고, 그 이후 어느 시점에서 시험을 중단하면 T* 는 T* > Tn이다. 식 (5)의 양변에 로그를 취하면 식 (6)과 같다.
∂lnL∂λ=0,∂lnL∂β=0으로부터 λ와 β의 최우추정치 λ^와 β⏜는 식 (7)과 같다.
3. K-00A1 체계의 신뢰도 성장 예측
다음은 총 2대의 K-000A1(장갑차)의 개발시험(DT)과 운용시험(OT) < Table 1>의 고장 데이터를 바탕으로 신뢰도 성장 모형을 적용 및 분석하고, 그 결과를 K-000A1의 개발 단계에서 예측한 Initial MTBF 값 (RAM분석 결과)과 비교 분석하였다.
3.1 적용 범위 및 방법
K-000A1(장갑차)는 크게 3가지의 서브시스템으로 구성되어 있고, 세부적으로는 19개의 모듈로 이루어져 있다. 예측하기에 앞서, 무기체계에서 어느 수준에 신뢰도 성장 모형을 적용할 것인지 결정하여야 한다. 정확도 측면에서 보면, 시스템 수준에서 시험을 실시하고 데이터를 수집하는 것이 합리적이고 정확한 방법이지만 현실적으로 큰 어려움이 존재한다. 따라서, 모듈 단위로 수집한 고장 데이터를 바탕으로 신뢰도 성장 모형을 적용하고 K-000A1의 신뢰도 성장 여부에 대한 판단과 신뢰도를 예측한다. 또한, K-000A1의 핵심 임무 기능에 관련되지 않고, 동체 및 장갑차체는 기존의 무기체계와 동일하여 과거 운용한 결과를 바탕으로 신뢰도가 어느 정도 보증되었다고 판단되어 일부 모듈을 제외하고 주요 모듈 7가지를 선정하였다. (고장 데이터가 없는 모듈 2개는 제외)
신뢰도 성장 예측은 Reliasoft RGA 7S/W를 이용하였고, Crow-AMSAA 모형을 적용하였다. 신뢰도 성장 예측은 개발시험과 운용시험을 구분하여 도출하였다. 또한, 주요 7가지 모듈에 대하여 각각의 신뢰도 성장 여부 및 MTBF를 추정하고, 이를 바탕으로 K-000A1(장갑차)도 분석한다.
3.2 신뢰도 성장 결과
K-000A1의 7가지 모듈에 대한 고장 데이터는 < Table 1>과 같으며, 개발시험과 운용시험에서 수행한 시험 기간은 < Table 2>와 같다. 먼저, 주요 7가지 모듈 중 상대적으로 고장 데이터가 많은 ‘B’ 모듈의 운용시험 고장 데이터에 대하여 RGA7 S/W를 사용하여 분석하였다. 다중시스템(Multiple Systems)에 대해 동시에 운용하여 수집한 고장 데이터를 바탕으로 신뢰도 성장 여부 및 MTBF를 추정하기 위해서는 < Figure 2>과 같이 ESS(Equivalent Single System)으로 변환하여 계산하여야 한다. ESS는 여러 가지 멀티시스템을 하나의 시스템으로 통합하는 방법으로 이 논문에서는 1호기와 2호기 고장시간을 하나의 고장시간으로 통합한 것이다. 따라서, K-000A1(장갑차)는 1, 2호기 총 2대를 운용시험에 사용하여 고장 데이터를 얻었기 때문에 ESS로 변환하여 분석하여야 하며, 변환한 결과는 < Figure 2>과 같다. 또한, ‘B’ 모듈에 대하여 MTBF와 고장강도 ρ^(T)를 시간 변화에 따라 나타낸 그래프는 < Figure 3>와 < Figure 4>과 같다. 그래프 분석 결과 MTBF는 시간에 따라 성장하고 있고, 고장강도 ρ^(T)는 감소하고 있으므로 신뢰도가 성장한다고 볼 수 있다. 여기서 ρ^(T)에서 T 값은 총 운용시간을 의미하며 1,302.88hr이다.
그리고 < Table 3>과 같이 성장률 모수 β^는 0.965, 고장강도 ρ^(T)는 0.014, MTBF는 74.007이다. 이는 모듈의 수명분포가 지수분포를 따른다는 강한 가정 하에 ‘MIL-HDBK-217'을 이용하여 예측한 값이다. 이와 같은 방법으로 수집한 고장 데이터를 이용하여 ‘A’부터 ‘F’까지 총 7가지 모듈에 대해 개발시험과 운용시험으로 구분하여 각각 MTBF, 성장률(Growth Rate), 고장강도를 도출하였고, 7가지 모듈 전체에 대한 결과도 구하였다. 또한, 각 모듈에 대하여 예측한 Initial MTBF 값 (RAM분석 결과)과 비교 분석하였으며, 그 결과는 < Table 4>와 같다. 분석한 결과, ‘A’, ‘B’, ‘D’, ‘E’ 모듈과 7가지 모듈 전체 대한 운용시험 데이터에서 구한 β이 0과 1사이의 값을 가지므로 신뢰도가 성장한다고 볼 수 있다. 하지만, ‘C’개발시험 데이터와 ‘G’ 모듈의 운용 시험 데이터가 없어서 Crow-AMSAA 모형에 적용할 수 없었다. 개발시험과 운용시험에서 수집한 고장 데이터에 대해 Crow-AMSAA 모형에 적용하여 구한 MTBF 값이 훨씬 낮은 것을 알 수 있다. 그러나, 신뢰도 성장 모형을 적용하여 도출한 MTBF 값이 RAM 분석 결과보다 훨씬 낮다고 하여 목표한 신뢰도를 충족하지 않았다고 할 수 없다. 왜냐하면 RAM 분석은 Series System과 각 Part 또는 모듈 의 수명분포가 지수분포를 따른다는 강한 가정 하에 ‘MIL-HDBK-217'을 이용하여 예측한 값으로, 실제 현실을 완벽하게 반영한다고 보기 어렵다. 그리고, 데이터의 수가 작은 모듈도 존재한다고는 하지만 개발시험과 운용시험에서 수집한 실제 시험 데이터를 바탕으로 도출한 MTBF 값이 상대적으로 RAM분석 결과 값보다 더 정확하다고 생각된다.
추가적으로, 모듈 7가지 전체에 대한 Crow-AMSAA 모형 결과와 RAM 분석을 비교하면 실제 시험데이터를 바탕으로 신뢰도 성장 모형을 적용하여 도출한 MTBF 값이 208.394hr으로 RAM 분석 결과 값인 151.70hr보다 높은 것을 알 수 있다. 또한, MTBF의 성장 그래프는 < Figure 5>과 같다.
4. 결 론
이 연구에서는 기동장비에 대한 신뢰성 활동 중 고객이 요구한 신뢰도 목표 값과 이를 달성하기 위한 방안의 일부인 신뢰도 성장(Reliability Growth) 모형을 D사에서 개발 한 K-000(장갑차)장비에 적용하여 분석하였다.
신뢰도 예측과 실적적용 사례를 비교 분석한 결과 신뢰도 성장하고 있음을 확인 할 수 있었다.
REFERENCES
Crow, L. H. 2006. Useful Metrics for Managing Failure Mode Corrective Action. Reliability and Maintainability Symposium. IEEE. pp 247-252.
John, Kleinberg 2007. AMSAA Reliability Scorecards. US Army Materiel Systems Analysis Activity.
Marguerite, Shepler 2010. New Army and DoD Reliability Scorecard. U.S. Army Materiel Systems Analysis Activity.
Michael, Cushing, E. Andrew, Long, and Margaret, Hockenberry 2009. Development of Reliability Program Standard GEIA-STD-0009. Reliability and Maintainability Symposium IEEE; 152-183.
Miguel, Peterson, and Wayne, Roberts 2014. Reliability Growth Analysis (RGA) for Missile Systems - RGA for Generic Cruise Missile. Raytheon Company.
MIL-HDBK-189C 2011. Reliability Growth Managemen. U.S. Department of Defense.
U.S. Department of Defense 2005. DoD Guide for Achieving Reliability, Availability and Maintainability.
U.S. Department of Defense 2008. Report of the Reliability Improvement Working Group (RIWG). Washington, DC. Govern-ment Printing Office.
Figure 1.
Reliability Growth Model Process 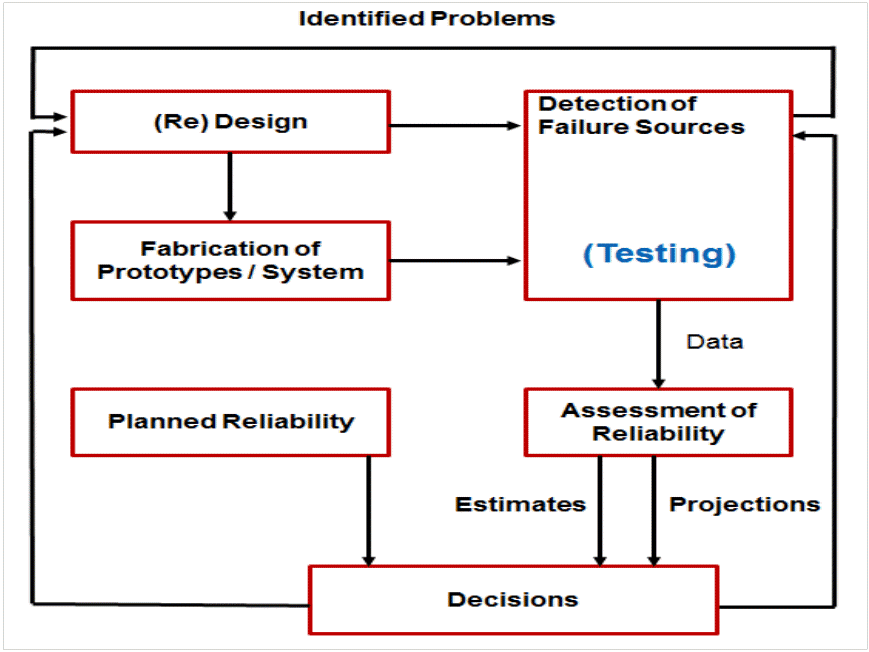
Figure 2.
ESS(Equivalent Single System) Graph of ‘B’ Module 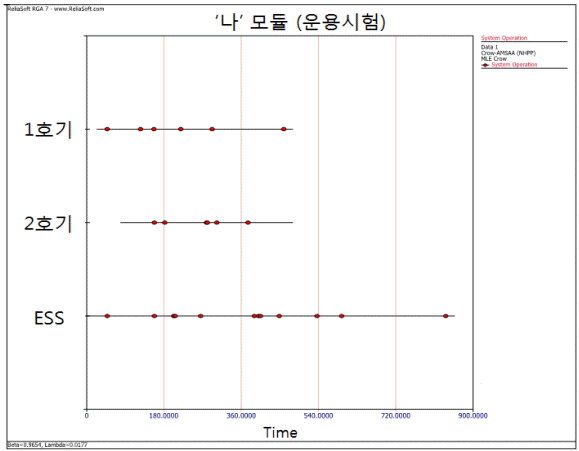
Figure 3.
MTBF vs Time Graph of 나’ Module 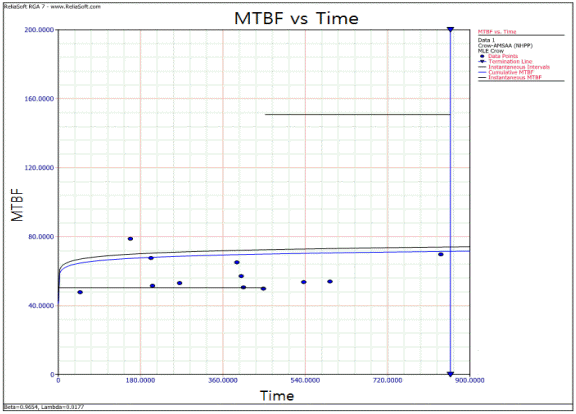
Figure 4.
Failure Strength ρ^(T) vs Time Graph of ‘나’ Module 
Figure 5.
MTBF Value of Each Module 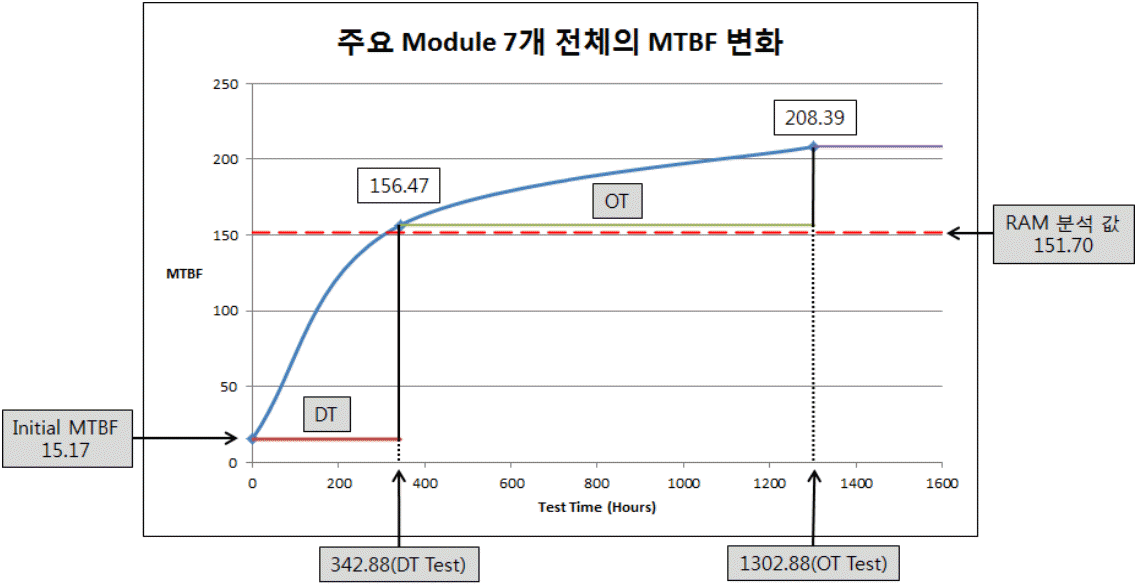
Table 1.
DT and OT Failure Data of K-000A1
|
모듈 |
시험 |
호기 |
고장 시점 |
|
가 |
DT/OT |
1 |
54.87 |
62.60 |
208.68 |
333.89 |
- |
- |
- |
- |
|
|
2 |
137.17 |
230.30 |
- |
- |
- |
- |
- |
- |
|
|
나 |
DT/OT |
1 |
47.74 |
125.21 |
156.51 |
219.12 |
292.15 |
459.10 |
- |
- |
|
|
2 |
164.61 |
157.58 |
181.82 |
278.79 |
281.21 |
303.03 |
375.76 |
- |
|
|
다 |
DT/OT |
1 |
104.34 |
125.21 |
- |
- |
- |
- |
- |
- |
|
|
2 |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
라 |
DT/OT |
1 |
68.59 |
83.47 |
104.34 |
114.77 |
135.64 |
354.76 |
- |
- |
|
|
2 |
54.87 |
137.17 |
157.58 |
181.82 |
242.42 |
254.55 |
303.03 |
351.52 |
|
|
마 |
DT/OT |
1 |
87.65 |
166.94 |
- |
- |
- |
- |
- |
- |
|
|
2 |
82.30 |
84.85 |
351.52 |
- |
- |
- |
- |
- |
|
|
바 |
DT/OT |
1 |
68.59 |
87.65 |
- |
- |
- |
- |
- |
- |
|
|
2 |
137.17 |
365.19 |
- |
- |
- |
- |
- |
- |
|
|
사 |
DT/OT |
1 |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
2 |
137.17 |
- |
- |
- |
- |
- |
- |
- |
Table 2.
|
1호기 |
2호기 |
합 계 |
|
개발시험 (DT) |
102.88hr |
240.00hr |
342.88hr |
|
|
운용시험 (OT) |
480.00hr |
480.00hr |
960.00hr |
|
|
합 계 |
582.88hr |
720.00hr |
1,302.88hr |
Table 3.
Analysis Result of ‘나’ Module
|
β^
|
ρ^(T)
|
MTBF |
MTBF (RAM analysis) |
|
‘나’ module |
0.965 |
0.014 |
74.007 |
648.66 |
Table 4.
Crow-AMSAA Module Application Result of Each Module
|
MODULE |
DT
|
OT
|
MTBF (RAM) |
|
β^
|
ρ^(T)
|
MTBF |
β^
|
ρ^(T)
|
MTBF |
|
가 |
1.337 |
0.008 |
128.220 |
1.008 |
0.004 |
238.043 |
839.95 |
|
|
나 |
1.363 |
0.004 |
251.627 |
0.965 |
0.014 |
74.007 |
648.66 |
|
|
다 |
- |
- |
- |
0.697 |
0,001 |
688.745 |
3003.97 |
|
|
라 |
1.244 |
0.011 |
91.888 |
0.869 |
0.012 |
80.485 |
374.56 |
|
|
마 |
1.363 |
0.004 |
251.627 |
0.833 |
0.003 |
288.060 |
1465.55 |
|
|
사 |
1.572 |
0.009 |
109.089 |
1.013 |
0.002 |
473.713 |
4444.83 |
|
|
아 |
1.092 |
0,003 |
314.108 |
- |
- |
- |
3241.01 |
|
|
Total |
1.534 |
0.006 |
156.466 |
0.866 |
0.005 |
208.394 |
151.70 |
|
|