다구찌 기법을 활용한 반도체 연마 공정의 최적 설계수준 결정
Abstract
Purpose
In this study, an optimal design level of influencing factors on semiconductor polishing process was determined to minimize flexion of both sides on wafers.
Methods
First, significant interactions are determined by the stepwise regression method. ANOVA analysis on SN ratio and mean of dependent variable are performed to draw mean adjustment factors. In addition, the optimal levels of mean adjustment factors are decided by comparing means of each level of mean adjustment factors.
Results
As a result of ANOVA, a mean adjustment factor was determined as a width of formed flexion on the plate. The mean of the difference has the nearest to 0 in the case when the width of formed flexion has level 2 (4mm).
Conclusion
Optimal design levels of semiconductor polishing process are determined as follows; (i) load applied to the wafer carrier has a level 1 (3psi), (ii) load applied to the wafer has a level 1(3psi), (iii) the amount of slurry supplied during polishing has a level 3 (300 co/min), (iv) the width of formed flexion on the plate has level 2 (4mm).
Key words: CMP(Chemical Mechanical Planarization), Taguchi Method, SN(Signal to Noise) Ratio, Robust Design
1. 서 론
반도체 소자는 고집적화를 위해 초미세크기의 선폭이 필요하다. 반도체 공정에서 미세한 선폭의 구조를 형성하는 해상능력이 향상될수록 초점 심도(depth of focus)는 감소하는 추세를 보인다. 이러한 원인은 다층 배선 형성 과정에서 발생하는 불규칙한 단차가 후속 공정에 치명적인 요소로 작용한다. 초점 심도의 여유를 확보하기 위해 기존에는 리플로우(reflow), SOG(Spin on Glass), EBP(Etch Back Process) 등의 기술을 사용해왔다. 그러나 이러한 국부적인 평탄화 기술은 미세 패터닝시에 필요한 광역 평탄화 요구를 만족할 수 없으므로, 새로운 광역 평탄화 기술이 필요하게 되었다. 따라서 대안 중에 반도체 연마 공정에서 기계적 연마와 화학적 연마를 동시에 수행하는 화학적-기계적 연마(CMP: Chemical Mechanical Planarization)가 대두되었다. CMP는 공정 중 공급되는 슬러리(slurry:나노 크기의 구형입자들을 알칼리 용액에 혼합해 놓은 것)의 화학적 작용과 슬러리 내 존재하는 입자를 이용하여 기계적 마찰을 이용한다. 따라서 웨이퍼(wafer)의 표면이 평탄화 되는 공정을 의미한다. 그러나 평탄화 공정을 거치면, 웨이퍼의 중앙부분은 균일하게 연마되는 반면에 양쪽 말단 부분은 굴곡이 생기는 경우가 발생한다. 이를 최소화하기 위해, 본 연구에서는 공정에 영향을 끼치는 인자들을 추출하여, 실험계획법의 하나인 다구찌(Taguchi) 기법으로 문제를 해결하고자 한다.
다구찌 기법은 품질을 ‘제품이 출하되어 사회에 끼치는 손실’로 정의한다. 제품이나 공정의 설계 단계에서 여러 조건의 잡음(Noise)의 변화를 파악하여, SN비(signal to noise) 등의 계량치로 변환하여 산포를 최소로 하는 인자들의 조건을 찾아가는 강건 설계이다. 그러므로, CMP 공정에 다구찌 방법을 적용하였을 때의 이점은 설계 시 최소한의 실험횟수를 통해서 잡음을 최소화하는 인자들의 조건을 알 수 있으므로, 시간과 비용 절감을 달성할 수 있다. 본 연구에서는 주효과와 일부 교호작용의 파악을 용이하게 할 수 있고, 실험횟수를 혁신적으로 감소시켜 경제성을 향상시키기 위해 직교배열표(Table of Orthogonal Array)를 이용하였다.
본 논문은 2장에서는 반도체 연마 공정에 대한 연구에 대한 관련 문헌을 살펴보고, 3장에서는 구체적인 실험목적과 문제 설명을 다룬다. 4장에서는 본격적으로 다구찌 기법의 핵심인 파라미터(Parameter) 설계로 분석을 한다. 5장에서 분석결과를 토대로 의미와 한계점을 살펴보고 연구결과를 전체적으로 요약한다.
2. 참고 문헌연구
CMP에 대한 연구는 2000년도 이후 활발하게 이루어지고 있다. 2000년대에는 주로 슬러리에 대한 연구가 이루어졌다. Jeong and Kim(2001)은 CMP 공정 중에 폐슬러리의 감소와 재활용 가능한 방법을 제안하였고 Lee et al.(2001)은 CMP 공정에서 슬러리와 패드의 종류에 따른 연마율을 연구하였다. 또한, Jeong et al.(2004)는 슬러리의 온도와 유량에 따른 연마율을 연구하였다. Seok et al.(2007)은 웨이퍼의 돌기와 연마 입자 사이의 기계적 효과를 고려하면서 패드 사이의 마찰로 인해 발생하는 열을 열전달 시스템으로 모델링하여 접촉역학과 화학적 연성효과를 고려하였다. 2010년대에 들어서는 슬러리외의 다른 요인을 통한 연구가 진행되었다. Cho et al.(2012)는 CMP 공정에서 발생하는 웨이퍼의 스크래치 발생을 최소화하기 위해, 합금을 사용하는 재료공학적 접근과 전기화학적인 평가를 통해 연구하였다. 또한 Kim and Hur(2014)는 CMP 공정 중 웨이퍼에 도포된 구리의 두께 측정의 정밀화로 제어시스템의 편차를 줄이는 방법을 연구하였다. 같은 해, Chung(2014)은 사파이어 웨이퍼의 파손을 방지하기 위한 슬러리 제조기술로 CMP 공정의 신뢰성 향상 및 분산안정성과 유효기간 증대를 위한 연구를 하였다. Lee and Jeong(2015)은 선형 롤 CMP 공정에서 슬러리 공급 장치의 조건에 따른 연마율에 대해 연구하였다. Jeong(2016)은 슬러리의 연마 입자에 따른 표면 제거율과 화학-기계적 균형에 대해 논의하였다. 그동안 CMP에 대한 연구는 주로 슬러리의 공급 방법과 입자, 온도, 유량 등의 요소에 한정하거나 웨이퍼의 재료 개선에 대한 연구가 주를 이루었다. 아직까지 관련문헌 연구를 통해서 다구찌 기법을 활용한 CMP 공정 최적화를 논의한 사례는 발견되지 않았다. 본 논문은 CMP 공정을 단순히 기계공학적, 재료공학적 접근이 아닌 파라미터 설계를 통해 공정의 인자를 선정하여 생산성 향상을 위해 연구하였다. 이러한 접근방법은 향후 반도체 산업 발전에 새로운 방법을 제시하는 것으로 의미가 있다고 사료된다.
3. 실험목적 및 문제 설명
3.1. 웨이퍼의 연마작업 소개
Figure 1은 규소(Si) 기판 위에 트랜지스터(transistor)와 금속배선을 형성할 때 생기는 표면 단차를 나타내고 있다. 표면 단차는 초점 심도의 변화를 야기하여 후속공정에 어려움을 준다. 그러므로 Figure 1과 같이, 반도체 제조공정에서 발생하는 웨이퍼의 표면 단차를 해소하기 위한 화학-기계적 연마를 이용한 평탄화 공정이 요구된다. 이와 더불어 평탄화는 미세구조에서 뿐만 아니라 웨이퍼 전면에 걸쳐 이루어져야 한다. CMP는 웨이퍼를 폴리머(polymer) 재질의 평판 위에서 적절히 선택된 슬러리를 공급 및 일정한 하중을 가해 운동시켜 이루어지고, Figure 2를 통해 그 과정을 표현하였다.
웨이퍼를 연마하게 되면, 중앙부분은 거의 평탄하게 이루어지나 양쪽 끝부분에서 서로 대칭을 이루며, 굴곡을 이루는 경우를 Figure 3을 통해 알 수 있다. 따라서, 본 연구는 양쪽 말단의 연마되는 정도, 즉 연마속도의 균일함을 목표로 하고 있다.
3.2. 변수 설정
실험인자는 웨이퍼의 연마속도에 영향을 미치는 5개의 인자를 선택하였고, Table 1과 같이 정리하였다.
위의 실험조건으로 실험을 수행하게 되면, Figure 3과 같이 웨이퍼의 가운데 부분은 연마율이 균질하게 나타나므로 측정하는 부분은 말단을 택한다. 또한 연마하는 방식이 동일한 선속도를 가지므로, 원점을 중심으로 같은 거리에서의 측정값은 대칭적이게 된다. 따라서 실제 측정값은 임의의 한 선상에서 이루어진다. 실제 측정값은 중앙에서 75mm, 80mm, 85mm, 90mm, 95mm 떨어진 지점에서의 위치별 연마속도를 측정한 것 이다. 위의 Figure 4는 이 설명을 이해하기 쉽게 도식화 한 것 이다.
4. 파라미터 설계
파라미터 설계는 성능 특성치에 영향을 주는 제어가능한 인자(controllable factors)를 최적수준으로 정해주는 것이다. 즉, 제품의 품질변동이 잡음에 둔감하면서 목표품질을 가질 수 있게 한다. 본 연구에서는 최적조건을 찾기 위해, 설계변수와 잡음을 주는 인자들을 포함시켜서 실험하는 직교배열표를 사용하였다. 본 연구에서는 3수준 5인자 실험이므로, L27(313) 직교배열표를 사용하였다. 이 때, 주효과가 5개이므로 L27 직교표에서 파악할 수 있는 교호작용은 3개 정도만 파악할 수 있다. 따라서, 교호작용을 파악하기 위해 y의 평균에 대한 단계적 회귀분석을 실시하였다. 특성치 y는 기준점인 z0값으로부터 z1~z4값이 얼마나 떨어져 있는지를 파악하기 위한 식으로, 다음과 같다.
본 연구는 웨이퍼 말단의 균일도(uniformity)를 높이기 위한 것으로 특성치의 목표값이 0인 망목특성이 된다. Table 2의 y값은 수식 (1)에 의하여 변환된 값이며, Table 3에서는 단계적 회귀분석을 통해 목표변수의 평균인 E(y)와 인자 A, B, C, D, E에 대해 분석한 것이다. 인자의 단계적 선택을 위해서, 입력할 변수를 위한 유의수준 및 제거할 변수를 위한 유의수준을 각각 0.15로 설정하였다. 그 결과, 유의수준이 0.05일 때, 유의한 인자는 A, B, C, A2, B2 ,C2 , A×C 이므로 교호작용 A×C만 파악하도록 하였다. 직교표의 주효과 및 교호작용의 배치는 Figure 5의 선점도를 이용하여 배치하였다.
4.1. SN비 산출 및 분석
SN비는 신호의 힘과 잡음의 힘의 비로서, 수식으로 나타내면 다음과 같다.
이고 데시벨(db) 단위로 나타내면,
수식 (3)과 같고 표현에 따라, 수식 (3)을 다음과 같이 나타낼 수도 있다. 이 때, 수식 (4)에 쓰인 MSD는 평균제곱편차라고 하며, 망목특성에 따라 인자의 종류가 상이하여, SN비에 사용하는 MSD의 값이 변화한다. 다음은 인자의 종류에 대한 설명이다. (1) 산포 제어인자: 인자수준에 따라 평균과 표준편차가 정량적으로 변한다. 이 때,
이므로 수식 (5)를 수식 (4)에 대입하면 SN비는 다음과 같다. (2) 평균 제어인자: 인자수준에 따라 표준편차의 변화가 없다. 이 때, MSD는 다음과 같으므로
수식 (7)을 수식 (4)에 대입하면 SN비는 다음과 같다. 반도체 연마 공정상의 인자들은 평균제어인자로 알려져 있다. 그러므로 수식 (8)을 사용하여 구한 SN비는 Table 4와 같다. 산출된 SN비를 통해 다구찌 기법으로 실험을 실시한 결과는 Table 5와 같다. 위의 수준별 평균 SN비를 보았을 때, A는 3수준, B 3수준, C 1수준, D 1수준, E 3수준이 됨을 알 수 있다. 이어서, 주효과의 유의성을 검정하기 위해 SN비의 분산분석을 수행해 본 결과는 다음과 같다.
분석 결과, p-value 값이 극단적으로 차이가 많이 나는 것을 알 수 있었다. Table 6에서 인자 B, D, A×B, B×C는 p-value 값이 모두 0.6를 초과했지만 나머지 인자 A, C, E, A×C는 p-value 값이 0.2 이하이므로 비교적 유의한 인자라고 판단할 수 있었다. 그러므로 Figure 6의 그래프와 함께 분석을 하면 최적 수준은 A는 3수준, C 1수준, E 3수준이 될 것 이다. 그러나 A×C의 교호작용이 매우 유의하기 때문에 A×C 교호작용을 파악할 필요가 있다. A×C 교호작용을 파악하기 위해 교호작용도를 작성한 결과는 Figure 7과 같다.
Figure 7의 교호작용도를 보면, 인자 A와 C가 모두 동 수준일 때, SN비가 가장 높음을 알 수 있었다. 각 수준에 대한 SN비 값은 차이가 미미하나 모두 1수준일 때가 다소 높기 때문에 인자 A와 C를 모두 1수준으로 결정하였다. 따라서, 교호작용 고려 후의 최적수준은 A1C1E3이며, 그 때의 최적 SN비는 26.1996이 된다.
다음 Table 7은 평균조정인자를 선정하기 위해서 목표변수의 평균에 대한 분산분석을 수행한 결과이다. 평균에 대한 분산분석 결과 유의한 인자는 A, B, C, A×B, A×C, B×C이나, 앞서 시행한 회귀분석 결과 유의한 교호작용은 A×C이므로 A×B와 B×C의 결과는 제외하기로 한다. 그러므로 SN비에 유의한 인자는 A, C, E, A×C였고, SN비에 유의하지 않으면서 평균에 대해서만 유의한 인자는 B이므로 평균조정인자는 B가 된다. SN비와 평균에 대한 분산분석 결과 인자 B가 평균조정인자임을 알 수 있었다. 그러므로 다른 인자는 고정시키고 B의 조정 수준을 알기 위해서 각 수준별 평균에 대한 주효과도를 그린 결과는 Figure 8과 같았다. 위의 그래프에서 평균조정인자 B만 고려하면 B가 2수준(4mm)일 때, 평균이 가장 낮음을 알 수 있었다. Figure 8에 따르면 2수준이 가장 평균이 0에 가깝고 그 다음은 3수준, 1수준이 제일 평균이 0에 가깝지 않다. 이를 확인하기 위해, 교호작용 고려 후 최적수준인 A1C1E3에서 인자 B가 1수준과 3수준을 가지는 추가 실험을 실시하였다. 실시 결과, B가 1수준을 가질 때는 0.0857450, 2수준일 때는 0.0414957, 3수준일 때는 0.0727641인 평균값이 산출되었다. B가 2수준 일 때 가장 평균치가 낮아 Figure 8의 그래프와 같은 양상을 보였다.
5. 결 론
본 연구에서는 반도체 연마 공정에서, 규소 기판 위의 트랜지스터와 금속배선을 형성할 때 생기는 표면 단차를 해소하기 위한 평탄화 공정에 대해 다루고 있다. 연구 목적은 평탄화를 위해 웨이퍼를 연마하게 되면, 웨이퍼의 말단 부분이 서로 대칭을 이루며 굴곡을 이루는 경우가 빈번하기 때문에 이를 해소하기 위함이다. 따라서 양쪽 웨이퍼의 말단이 중앙처럼 균일하게 평탄화 되기 위해서는 연마속도가 균일하게 되어야 한다는 의미이다. 그러므로 연마속도의 영향을 끼칠 수 있다고 판단되는 인자 5가지를 결정하여 데이터를 산출하였다. 산출한 데이터를 다구찌 기법을 활용해서 적은 실험횟수로 가장 효율적인 공정 수준을 찾을 수 있는 것에 의미를 찾을 수 있었다.
다인자로 반복하는 시행하는 실험이므로 우선 교호작용을 파악하기 위해서 단계적 회귀분석으로 인자 A×C가 유의한 교호작용임을 파악하였다. 그 후, E(y)와 SN비를 산출하였다. 산출한 SN비와 E(y)를 인자들과 각각 분산분석을 하였다. 그 결과, SN비에 유의하지 않으면서 E(y)에 유의한 인자를 찾아냈다. 그 과정에서 인자 D는 수준에 따른 영향의 거의 끼치지 않는 사실도 알 수 있었다. 이러한 일련의 과정을 통해, 인자 B의 수준을 조정하여 2수준 일 때가 최적 수준임을 알 수 있었다. 즉, 평판 위에 형성된 홈의 폭이 4mm 일 때가 가장 최적임을 파악하였다.
REFERENCES
Byun, J-H., Kim, Y. T., and Lee, M. J. 2013. Understanding Robust Design with Paper Helicopter Experiment. Journal of the Korean Institute of Industrial Engineers 39(5):374-382.  Cha, K. J., and Chin, C. U. 2000. The Optimal Design of Low Noise Intake System Using Taguchi Mehod with Non-controllable Factors. J Korean Soc Qual Manag 28(1):41-56.
Cho, B-J., Kwon, T-Y., Kim, H-M., Venkatesh, P., Park, M-S., and Park, J-G. 2012. Electrochemical Characterization of Anti-Corrosion Film Coated Metal Conditioner Surfaces for Tungsten. Journal of the Microelectronics and Packaging Society 19(1):61-66.  Chung, C. H. 2014. Mixed Nano Silica Colloidal Slurry for Reliability Improvement of Sapphire Wafer CMP Process. Journal of Applied Reliability 14(1):11-19.
Hong, S. P., Kim, S. M., Park, S., and Jung, E. S. 2001. A Study on Designing of a Menu Structure for the Instrument Cluster IVIS using Taguchi Method. Journal of the Ergonomics Society of Korea 29(1):39-46.  Jeong, H. D. 2016. Chemical-Mechanical Balance of CMP. Journal of Mechanical Science and Technology 52(428):36-39.
Jeong, H. D., and Kim, H. Y. 2001. Eco-process in a Semiconductor Manufacturing process. Journal of the Korean Society of Precision Engineering 18(9):25-30.
Jeong, Y., Kim, H., Choi, J., and Jeong, H. 2004. The Effect of Slurry Flow Rate and Temperature on CMP Characteristic. Journal of the Korean Society of Precision Engineering 21(11):46-52.
Kim, N-W., and Hur, C-W 2014. A Study of Data correction method when in-situ end point detection in Chemical-Mechanical Polishing of Copper Overlay. Journal of the Korea Institute of Information and Communication Engineering 18(6):1401-1406.  Kwon, O-H., Koo, P-H., and Kwon, H-M. 2016. Taguchi-based robust design for the footwear outsole. J Korean Soc Qual Manag 44(4):935-949.   Lee, C., and Jeong, H. 2015. A Study on the Polishing Characteristics Using Floating Nozzle in Linear Roll CMP. Journal of the Korean Society of Precision Engineering 32(7):627-631.  Lee, J. C., Hong, J. K., and Yoo, H. D. 2001. Planarization & Polishing of single crystal Si layer by Chemical Mechanical Polishing. Journal of the Korean Vacuum Society 10(3):361-367.
Ree, S. 2013. Study on the Result Changes with the Size of the Variance in Taguchi Method and Factor Experimental. J Korean Soc Qual Manag 41(1):119-134.  Seok, J., Oh, S., and Seok, J. 2007. An Analysis on the Material Removal Mechanism of Chemical-Mechanical Polishing Process Part I: Coupled Integrated Material Removal Modeling. Journal of the Semiconductor & Display Equipment Technology 6(2):35-40.
Yang, I-M., Oh, G., Yoo, C-B., and Hwang, I. 2015. Design and Analysis of Experiments. Seoul. Minyoungsa.
Yun, W. Y., and Seo, S-K. 2013. Determining the Level of A Noise Factor in Parameter Design for Smaller-the-better Characteristics. Journal of the Korean Institute of Industrial Engineers 39(5):367-373. 
Figure 1.
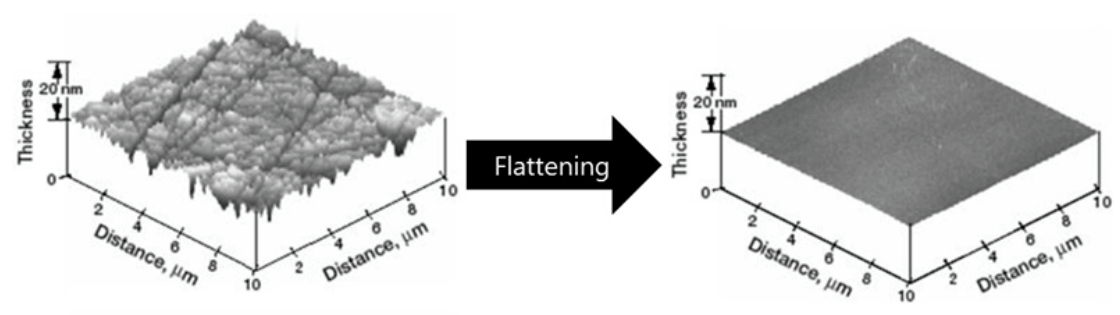
Figure 2.
Schematic diagram of CMP process 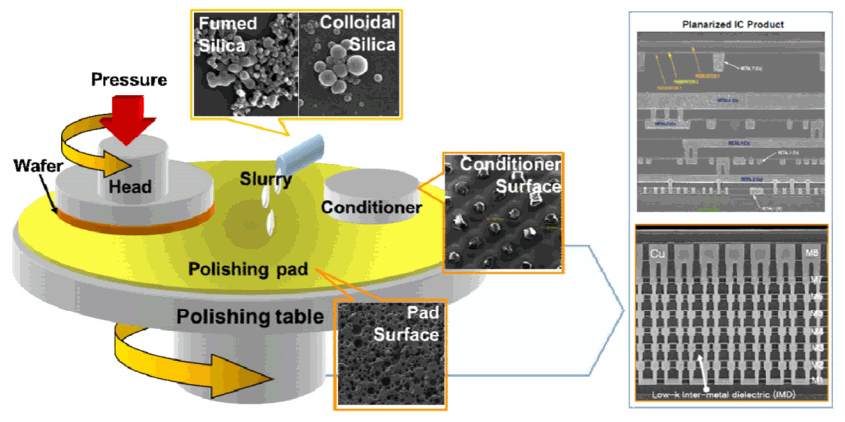
Figure 3.
Wafer image after Polishing 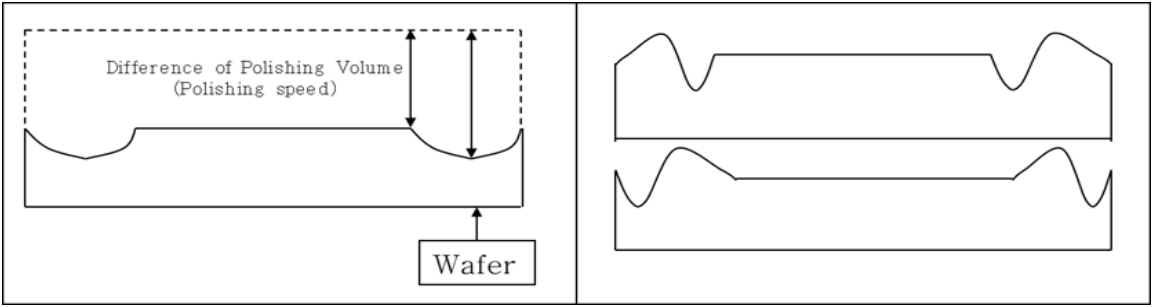
Figure 4.
Diagram of type of measurement 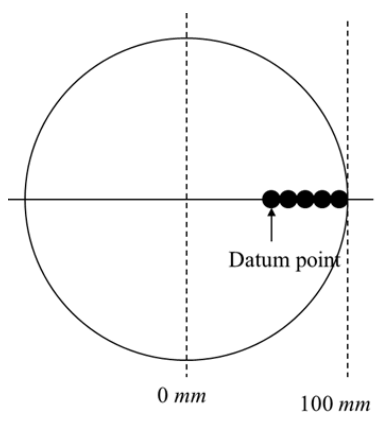
Figure 5.
Line and dot diagram of 3 level system(L27(313) type) 
Figure 6.
Main effects plot for SN ratios 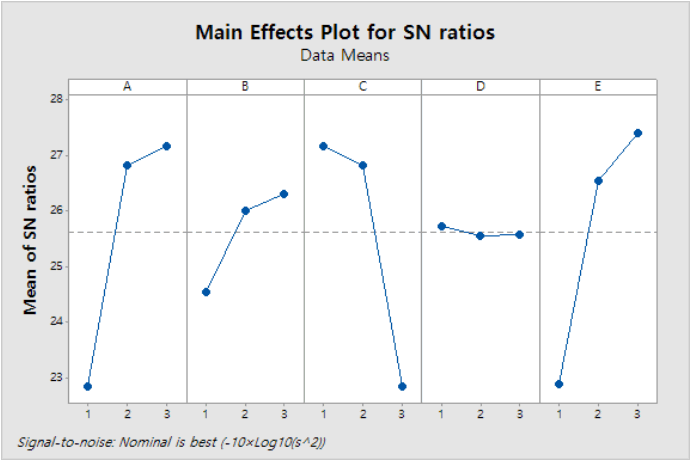
Figure 7.
Interaction plot for SN ratios 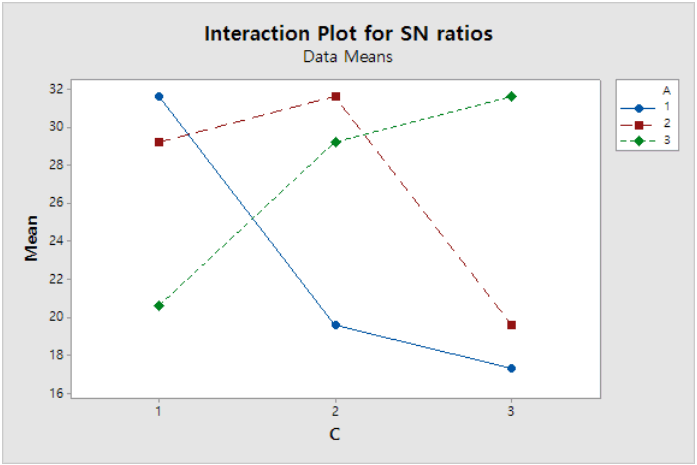
Figure 8.
Main effects plot for means 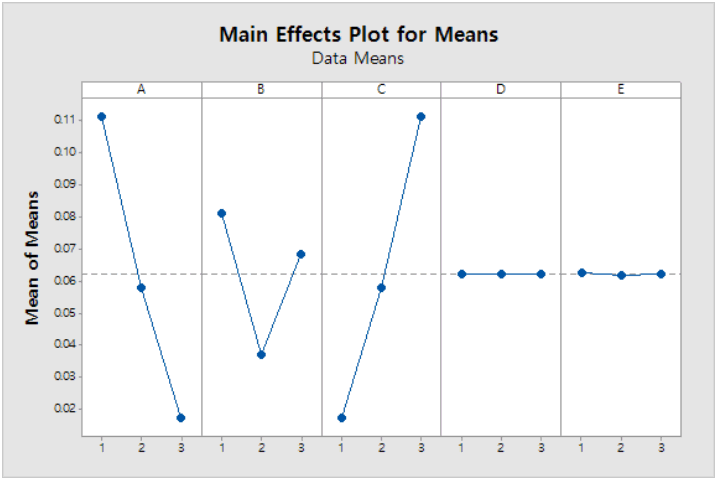
Table 2.
Control factors and level
|
Control Factors |
Level
|
|
1 |
2 |
3 |
|
A : Load applied to the wafer carrier(psi) |
3 |
5 |
7 |
|
|
B : Width of formed flexion on the plate(mm) |
2 |
4 |
6 |
|
|
C : Load applied to the wafer(psi) |
3 |
5 |
7 |
|
|
D : Movement speed of wafer(cm/s) |
60 |
80 |
100 |
|
|
E : The amount of slurry supplied during polishing(co/min) |
100 |
200 |
300 |
Table 3.
|
z0 |
z1 |
z2 |
z3 |
z4 |
y1 |
y2 |
y3 |
y4 |
E(y) |
|
1004 |
992 |
945 |
920 |
870 |
0.0120 |
0.0588 |
0.0837 |
0.1335 |
0.0720 |
|
|
2051 |
2115 |
1929 |
1672 |
1465 |
-0.0312 |
0.0595 |
0.1848 |
0.2857 |
0.1247 |
|
|
3410 |
3449 |
3003 |
2510 |
2135 |
-0.0114 |
0.1194 |
0.2639 |
0.3739 |
0.1864 |
|
|
1235 |
1188 |
1182 |
1230 |
1209 |
0.0381 |
0.0429 |
0.0040 |
0.0211 |
0.0265 |
|
|
2425 |
2432 |
2320 |
2147 |
1956 |
-0.0029 |
0.0433 |
0.1146 |
0.1934 |
0.0871 |
|
|
2366 |
2327 |
2120 |
1892 |
1673 |
0.0165 |
0.1040 |
0.2003 |
0.2929 |
0.1534 |
|
|
1455 |
1365 |
1368 |
1409 |
1339 |
0.0619 |
0.0598 |
0.0316 |
0.0797 |
0.0582 |
|
|
1545 |
1512 |
1451 |
1330 |
1172 |
0.0214 |
0.0608 |
0.1392 |
0.2414 |
0.1157 |
|
|
2885 |
2769 |
2537 |
2243 |
1919 |
0.0402 |
0.1206 |
0.2225 |
0.3348 |
0.1795 |
|
|
1255 |
1247 |
1200 |
1193 |
1207 |
0.0064 |
0.0438 |
0.0494 |
0.0382 |
0.0345 |
|
|
2405 |
2378 |
2263 |
2205 |
2084 |
0.0112 |
0.0590 |
0.0832 |
0.1335 |
0.0717 |
|
|
2335 |
2407 |
2196 |
1903 |
1668 |
-0.0308 |
0.0595 |
0.1850 |
0.2857 |
0.1248 |
|
|
1427 |
1379 |
1389 |
1474 |
1551 |
0.0336 |
0.0266 |
-0.0329 |
-0.0869 |
-0.0149 |
|
|
1534 |
1475 |
1469 |
1528 |
1501 |
0.0385 |
0.0424 |
0.0039 |
0.0215 |
0.0266 |
|
|
2903 |
2912 |
2778 |
2571 |
2342 |
-0.0031 |
0.0431 |
0.1144 |
0.1932 |
0.0869 |
|
|
1014 |
956 |
968 |
1018 |
1036 |
0.0572 |
0.0454 |
-0.0039 |
-0.0217 |
0.0192 |
|
|
2066 |
1939 |
1941 |
2001 |
1902 |
0.0615 |
0.0605 |
0.0315 |
0.0794 |
0.0582 |
|
|
3395 |
3323 |
3188 |
2923 |
2576 |
0.0212 |
0.0610 |
0.1390 |
0.2412 |
0.1156 |
|
|
1451 |
1385 |
1351 |
1456 |
1542 |
0.0455 |
0.0689 |
-0.0034 |
-0.0627 |
0.0121 |
|
|
1572 |
1562 |
1504 |
1495 |
1512 |
0.0064 |
0.0433 |
0.0490 |
0.0382 |
0.0342 |
|
|
2846 |
2814 |
2678 |
2610 |
2466 |
0.0112 |
0.0590 |
0.0829 |
0.1335 |
0.0717 |
|
|
1021 |
948 |
967 |
1120 |
1225 |
0.0715 |
0.0529 |
-0.0970 |
-0.1998 |
-0.0431 |
|
|
2059 |
1991 |
2004 |
2127 |
2238 |
0.0330 |
0.0267 |
-0.0330 |
-0.0869 |
-0.0151 |
|
|
3379 |
3250 |
3236 |
3367 |
3307 |
0.0382 |
0.0423 |
0.0036 |
0.0213 |
0.0263 |
|
|
1247 |
1130 |
1159 |
1330 |
1408 |
0.0938 |
0.0706 |
-0.0666 |
-0.1291 |
-0.0078 |
|
|
2414 |
2278 |
2306 |
2425 |
2468 |
0.0563 |
0.0447 |
-0.0046 |
-0.0224 |
0.0185 |
|
|
2372 |
2227 |
2229 |
2298 |
2184 |
0.0611 |
0.0603 |
0.0312 |
0.0793 |
0.0580 |
Table 4.
Analysis of variance of regression analysis: E(y) versus A, B, C, D, E
|
Source |
DF |
Adj SS |
Adj MS |
F-Value |
P-Value |
|
Regression |
9 |
0.092006 |
0.010223 |
1011.56 |
0.000 |
|
|
A |
1 |
0.000321 |
0.000321 |
31.74 |
0.000 |
|
|
B |
1 |
0.006582 |
0.006582 |
651.24 |
0.000 |
|
|
C |
1 |
0.000427 |
0.000427 |
42.26 |
0.000 |
|
|
A2 |
1 |
0.000237 |
0.000237 |
23.47 |
0.000 |
|
|
B2 |
1 |
0.008554 |
0.008554 |
846.46 |
0.000 |
|
|
C2 |
1 |
0.000249 |
0.000249 |
24.69 |
0.000 |
|
|
A×B |
1 |
0.000032 |
0.000032 |
3.18 |
0.092 |
|
|
A×C |
1 |
0.002348 |
0.002348 |
232.29 |
0.000 |
|
|
B×C |
1 |
0.000030 |
0.000030 |
2.98 |
0.103 |
|
|
Error |
17 |
0.000010 |
0.000010 |
|
|
|
|
Total |
26 |
|
|
|
|
Table 5.
|
E(y) |
Var(y) |
SN ratio |
|
0.071962151 |
0.002565022 |
25.90908886 |
|
|
0.124695271 |
0.019365179 |
17.12978474 |
|
|
0.18643695 |
0.028267236 |
15.48716651 |
|
|
0.026518219 |
0.000312249 |
35.05498927 |
|
|
0.087113402 |
0.007358217 |
21.3322739 |
|
|
0.1534235 |
0.014284142 |
18.45145832 |
|
|
0.058247423 |
0.000395327 |
34.0304377 |
|
|
0.115695793 |
0.009422154 |
20.25849811 |
|
|
0.179549393 |
0.016283111 |
17.88262606 |
|
|
0.034462151 |
0.00037137 |
34.30193455 |
|
|
0.071725572 |
0.002588105 |
25.87018032 |
|
|
0.1248394 |
0.019327217 |
17.13830687 |
|
|
-0.014891381 |
0.003196397 |
24.95339235 |
|
|
0.026564537 |
0.000310045 |
35.08575815 |
|
|
0.086892869 |
0.007362118 |
21.32997199 |
|
|
0.019230769 |
0.001445574 |
28.39959692 |
|
|
0.058204259 |
0.000393184 |
34.05403979 |
|
|
0.115611193 |
0.009409228 |
20.26445996 |
|
|
0.012060648 |
0.003393969 |
24.69292072 |
|
|
0.034192112 |
0.00036376 |
34.39185651 |
|
|
0.07167955 |
0.002587745 |
25.87078513 |
|
|
-0.043095005 |
0.016601419 |
17.79854785 |
|
|
-0.015055852 |
0.003181993 |
24.97300744 |
|
|
0.026339154 |
0.000313375 |
35.03936047 |
|
|
-0.007818765 |
0.011546075 |
19.37565639 |
|
|
0.018537697 |
0.001440709 |
28.41423655 |
|
|
0.05796796 |
0.000395103 |
34.03289907 |
Table 6.
Response Table for Signal to Noise Ratios
|
Level |
A |
B |
C |
D |
E |
|
1 |
22.84 |
24.53 |
27.17 |
25.72 |
22.88 |
|
|
2 |
26.82 |
26 |
26.83 |
25.55 |
26.54 |
|
|
3 |
27.18 |
26.3 |
22.83 |
25.56 |
27.42 |
|
|
Delta |
4.34 |
1.77 |
4.34 |
0.17 |
4.54 |
|
|
Rank |
2 |
4 |
3 |
5 |
1 |
Table 7.
Analysis of variance of SN ratio versus A, B, C, D, E
|
Source |
DF |
Adj SS |
Adj MS |
F-Value |
P-Value |
|
A |
2 |
104.49 |
52.247 |
2.82 |
0.172 |
|
|
B |
2 |
16.14 |
8.068 |
0.44 |
0.674 |
|
|
C |
2 |
104.76 |
52.379 |
2.83 |
0.172 |
|
|
D |
2 |
0.15 |
0.077 |
0.00 |
0.996 |
|
|
E |
2 |
104.19 |
52.096 |
2.81 |
0.173 |
|
|
A×B |
4 |
48.74 |
12.186 |
0.66 |
0.653 |
|
|
A×C |
4 |
700.88 |
175.220 |
9.46 |
0.026 |
|
|
B×C |
4 |
48.63 |
12.158 |
0.66 |
0.654 |
|
|
Error |
4 |
74.12 |
18.531 |
|
|
|
|
Total |
26 |
1202.11 |
|
|
|
Table 8.
Analysis of Variance of mean versus A, B, C, D, E
|
Source |
DF |
Adj SS |
Adj MS |
F-Value |
P-Value |
|
A |
2 |
0.040266 |
0.020133 |
38464.97 |
0.000 |
|
|
B |
2 |
0.009313 |
0.004656 |
8896.13 |
0.000 |
|
|
C |
2 |
0.040017 |
0.020009 |
38227.49 |
0.000 |
|
|
D |
2 |
0.000000 |
0.000000 |
0.25 |
0.789 |
|
|
E |
2 |
0.000001 |
0.000000 |
0.85 |
0.493 |
|
|
A×B |
4 |
0.000096 |
0.000024 |
45.75 |
0.001 |
|
|
A×C |
4 |
0.002388 |
0.000597 |
1140.36 |
0.000 |
|
|
B×C |
4 |
0.000095 |
0.000024 |
45.42 |
0.001 |
|
|
Error |
4 |
0.000002 |
0.000001 |
|
|
|
|
Total |
26 |
0.092178 |
|
|
|
|
|