1. 서 론
대기오염이 인간의 건강에 부정적인 영향을 주는 것은 오래전부터 잘 알려져 있다. 전 세계적으로 대기 오염에 의한 질환은 지속적으로 증가하고 있으며, 세계보건기구는 대기오염에 의한 사망자의 수가 약 700만 명에 이른다고 추정하고 있다(WHO, 2014). 대기오염 중 아황산가스는 만성폐질환과 호흡장애 등을 일으키며 오존, 미세먼지 등의 노출은 호흡기 및 심혈관계 질환의 발생과 관련이 있으며 사망률도 증가시키는 것으로 보고되고 있다(Pope, 2002).
현재에도 모든 나라에서 대기오염 문제가 주목 받고 있다. 현재까지 대기오염이 질환이나 사망에 영향을 미치는 것은 알려졌지만 대기오염의 종류, 농도에 따라 각 질환에 미치는 영향을 규명하는 연구는 많지 않다. 또한, 대부분 단기간의 영향을 조사하고 있다. 본 연구에서는 2005년부터 2013년까지 한국의 대기오염지수와 순환기 질환 표준화 사망자 수의 관계를 다루고 있다. 연구 결과를 기초로 향후 지속적인 연구를 통해 대기오염에 의한 질환의 예방 및 관리에 근거가 될 수 있을 것으로 생각한다. 본 연구에서는 SaTScan™9.3.1을 이용하여 대기오염과 질환의 발생이 높은 위험 지역의 클러스터를 결정한다. 또한, 이 결과를 시각화하여 지역적 분포를 살펴보고 대기오염과 질환 사망자 수 사이의 통계적 모형을 연구하고자 한다. 통계적 기법을 사용한 데이터 분석 모형을 추정할 때, 일반적으로 최소제곱법을 통해 모수를 추정하는 OLS(Ordinary Least Squares) 회귀분석 방법이 사용된다. 이는 위치에 따른 차이가 없다고 간주한다. 그러나 지역 단위로 수집한 자료는 공간적으로 근접한 위치일수록 서로 높은 상관이 있다. 따라서 일반적인 회귀분석 방법보다 공간적인 상관성을 고려한 지리가중회귀분석(GWR; Geographically weighted regression)을 이용하여 모형을 추정하는 것이 바람직하다. 이를 통해 질환 사망자 수에 영향을 미치는 대기오염을 규명하고 공간 자료의 분석에 있어 지리가중회귀모형 적용의 유용성을 검토하고자 한다. 또한, 지리가중회귀분석을 사용하여 추정된 회귀계수를 K-means 군집분석을 통해 대기오염의 지역적 분포의 특성을 살펴보았다.
2절에서는 위험 지역 탐색을 위한 포아송 분포를 바탕으로 한 우도비(Likelihood Ratio) 검정법과 대기오염과 질환의 공간적 상관분석을 위한 지리적 가중회귀분석을 소개하였다. 3절에서는 자료에 설명과 모형 설정을 소개하였으며, 4절에서는 대기오염과 질환의 시공간적 분포와 위험지역을 시각화하여 비교하고 이들 사이의 통계적 모형을 연구하였다. 참고로 본 논문에서는 2005년, 2009년, 2013년 자료의 분석만 게재를 하였고, 매년 자료에 대한 분석 결과는 박진옥(2016)을 참고하면 된다. 마지막으로 5절은 요약 및 결론으로 구성되어 있다.
2. 지리가중회귀분석(Geographically weighted regression)
지리가중회귀분석은 공간 단위로 수집된 자료를 분석할 때 쓰이는 기법이다. 도시 및 지역에서 수집된 공간 자료는 근접한 위치에서 수집된 사례일수록 더 높은 관련성을 가지는 특징이 있다. 이를 공간적 자기상관이라고 하며 이는 데이터의 집계로 인해서 발생하거나 공간상에서 인접함으로써 나타나는 파급효과로 풀이할 수 있다(이희연·노승철, 2012). 이러한 공간적 특징으로 인해 공간적 의존성과 공간적 이질성이 있는 데이터를 일반적으로 사용하는 OLS 회귀분석으로 추정하게 되면 오류가 발생하게 된다. OLS 회귀분석은 종속 변수가 상호 독립적이고 오차들도 상호 독립적이며 등분산성을 가정하므로 공간의 이질성에 의한 공간적 변이를 고려하지 못한다. 따라서 공간적 자기상관이 통계적으로 유의하게 나타난다면 회귀모형의 가정을 위배하게 된다. 이런 경우 OLS 회귀분석을 사용하게 되면 지역적 특성을 반영하지 못하고 모수 추정의 효율성이 떨어지게 된다. 이러한 공간 데이터의 문제점을 해결하기 위해 공간적 이질성을 고려한 다양한 공간통계 분석기법이 발전되어 왔으며, 그 중 Fotheringham et al.(2002)에 의해 개발된 지리가중회귀분석이 가장 많이 활용되고 있다.
지리가중회귀분석은 지역 간에 서로 다르다는 것을 전제하여 지역별로 서로 다른 회귀모형을 추정한다. 공간적 이질성이 존재하는 경우 설명변수와 종속변수가 같은 위치에 있는 것이 아니므로 설명변수가 같은 정도로 변화하더라도 그것의 영향을 받는 종속변수는 크기는 공간적 위치에 따라 달라진다. 이와 같은 공간적 이질성으로 발생하는 이분산성을 해결하기 위해 지리가중회귀모형에서는 가중치를 사용한다. 즉, 지리가중회귀모형은 지역 간 거리가중행렬을 이용하여 지리적 위치 에 따른 변수 에 대한 지역별 회귀계수를 추정하는 것이다. 지리가중회귀모형의 기본 식은 다음과 같이 나타낼 수 있다.
지리가중회귀모형에서 모수를 추정할 경우 OLS 회귀모형의 원리를 따라 추정 한다. 따라서 회귀계수에 대한 가중이 이루어진다는 점에서 가중최소자승법(Weighted Least Square: WLS)의 일종으로 볼 수 있으며, 다만 연구대상 지역 내의 위치에 따라 가중치가 달라진다는 차이가 있다. 이에 따라 회귀계수에 대해 위치에 따른 가중치가 부여되고 가중최소자승법에 따른 추정은 다음과 같이 이루어진다.
여기서 공간가중행렬 Wi는 i번째 관측값과 다른 모든 관측값을 반영하는 공간행렬로, i번째 관측값의 거리에 기초한 가중치 di를 포함하는 n×n 대각행렬이다.
공간가중행렬을 구축하는 경우, 공간가중행렬의 각 요소는 가중 함수인 커널(kernel)에 따라 계산된다. 커널은 다양한 형태를 취할 수 있지만 일반적으로 다음과 같은 가우스 형태의 식을 사용한다.
여기서 d는 i회귀점과 관찰치 j까지의 거리이며, θ는 대역폭(Bandwidth)이다. 대역폭이 커질수록 동일한 거리에 대한 가중치는 1에 가까운 값을 가지게 되며, 이러한 경우 OLS 회귀분석과 결과가 같아진다. 반면에 대역폭이 작아질수록 동일한 거리에 대한 가중치는 0에 가까운 값을 가지게 된다.
지리가중회귀분석의 결과는 지리함수의 종류보다 대역폭의 선택에 의한 영향을 받게 된다. 대역폭은 i회귀점과 관찰치 j까지의 거리를 일정하게 정한 후 분석을 하는 고정적 커널(Fixed kernel)과 각 회귀지점의 대역폭을 달리 정하는 가변적 커널(Adaptive kernel)이 있다. 연구대상 지역에서 표본점들이 규칙적으로 분포한 경우에는 고정된 대역폭을 사용해도 되지만 표본점들이 불규칙적으로 분포한 경우에 고정된 대역폭을 사용하게 되면 모형의 적합도가 떨어지게 된다. 고정된 대역폭은 표본점들이 밀집된 곳에서는 미묘한 공간적 차이를 포착할 수 없고, 표본점들이 분산된 곳에서는 추정치의 분산을 증가시키는 위험이 있다. 따라서 표본점들이 불규칙적으로 분포한 경우에는 표본점이 조밀한 곳에서는 대역폭을 작게, 조밀하지 않은 곳에서는 대역폭을 넓게 하는 가변적 대역폭이 모형의 적합도를 증가시킬 수 있다. 적정한 대역폭을 설정하기 위한 검정 방법으로는 관찰 값과 추정값 간의 차이 교차검증 CV(Cross Validation)를 최소화하는 방법과 관찰 값과 추정값 간의 차이 및 모형의 적합성을 판정하는 AIC(Akaike Information Criterion)가 있다. AIC 값을 최소화하는 대역폭을 선택하는 것이 바람직하다. AIC는 동일한 종속변수에 대해 상이한 독립변수로 구성된 모형을 비교하는 데 유용하며, 전역모형(OLS 모형)과 지역모형(지리가중회귀모형)을 비교하는 데에도 사용된다. 일반적으로 비교되는 두 모형에서 AIC 값의 차이가 2 또는 4보다 작은 경우 두 모형은 사실상 차이가 없는 것으로 본다.
회귀분석모형 잔차의 공간적 자기상관성을 측정하기 위해 가장 많이 사용되는 지표는 Moran I 통계량이며 이에 대한 식은 다음과 같다.
여기서 n은 지역단위 수, y
산출된 Moran I 지수 Z검정을 통해 통계적 유의성을 판정하게 된다. Moran I 지수 -1에서 1사이의 값을 가지게 되며, 1일 때 완전한 양의 자기상관, -1일 때 완전한 음의 자기상관관계가 있음을 의미한다. 유사한 값을 가지고 있는 지역들이 인접하는 경향이 강할수록 1에 가까운 값을 갖게 된다. 반면에 -1에 가까워질수록 큰 값과 작은 값을 가진 지역들이 규칙적으로 섞여서 분포해있다고 볼 수 있다. Moran I 지수는 유사한 값의 공간적 자기 상관을 측정하는 지수이므로 큰 값들이 군집된 경우나 작은 값들이 군집된 경우를 구분하지 못한다. 따라서 큰 값들과 작은 값들이 공간적으로 밀집해 있는 경우 모두 동일하게 자기상관도가 크게 산출된다.
Moran I 지수의 통계적 유의성 검정을 통해 공간적 자기상관을 판정하여 공간적 자기상관이 존재한다면 지리가중회귀분석으로 모형을 추정하고, 공간적 자기상관이 없는 것으로 판정되면 단순회귀분석으로 모형을 추정하는 것이 가능하다.
3. 자료와 모형 설정
본 연구를 수행하기 위하여 2005년부터 2013년까지 한국의 대기오염 자료와 순환기 질환 표준화 사망자 수 자료를 사용하였다. 대기오염 자료는 국립환경과학원에서 해당 지역의 도시대기측정망과 도로변대기측정망에서 측정한 자료로 관심 변수는 이산화황(SO2), 미세먼지(PM10), 오존(O3), 이산화질소(NO2), 일산화탄소(CO)가 있다. 대기오염은 관측소별로 해당 연도 1월 1일 1시부터 12월 31일 24시까지 시간 마다 농도가 측정 되었다. 순환기질환 표준화 사망자 수 자료는 국가통계포털(KOSIS)에서 수집한 자료로 시군구별 연령구조를 보정하기 위해 계산된 인구 10만 명당 연령표준화 사망률이다. 대기오염과 관련된 많은 질환 중 특히 순환계통 질환(고혈압성 질환, 심장 질환, 허혈성 심장 질환, 기타 심장 질환, 뇌혈관 질환)에 미치는 영향을 보고자 한다. 본 연구에서는 2012년 시군구(총 251개 구역)를 기준으로 하여 대기오염과 질환의 지역별 분포를 살펴보았으며 대기오염의 농도는 연도별 평균값을 사용하였고 결측값은 해당 연도 전후로 가장 가까운 연도의 관측값의 평균값을 사용하였다.
스캔 통계는 Joseph Naus(1965)가 직선과 평면상에서 관측점의 군집화 경향을 검정하기 위해 개발한 통계량이다. 본 연구에서 질환에 의한 사망자의 위험이 큰 지역의 클러스터링을 결정하기 위해 시공간 스캔통계량을 이용하는 소프트웨어 SaTScan™9.3.1(Martin Kulldorff, Boston, MA, USA)을 사용하였다. 관심 지역의 통계적 클러스터는 SaTScan의 우도비에 따라 지도에 표시 되는데, 본 연구에서 수집된 자료의 특성을 고려하여 적용한 포아송 모델의 우도비 γ는 다음과 같다.
여기서, C는 전체 값을 나타내며 c는 측정값이다. E(c)는 측정값의 기대 값이며 I()는 지시함수이다. Kulldorff는 Monte Carlo 검정법을 사용하여 질환에 의한 사망자의 위험이 큰 지역을 검정하였다.
공간적 변이를 고려하는 분석 과정에서 전역적 모형(global model)과 국지적 모형(local model)으로 구분할 수 있다. 전역적 모형은 공간상의 분포에 차이가 없다는 가정에 따라 분석하는 것이며, OLS 회귀모형이 전역적 모형에 해당한다. 반면에 전역적 모형을 분해하여 공간의 위치에 따른 차이를 추정하는 모형은 국지적 모형으로 지리가중회귀모형이 이에 해당한다.
본 연구에서 전역적 모형의 종속변수에 해당하는 것은 순환기계통 질환의 사망자 수이며, 독립변수에 해당하는 것은 각 대기오염 지수이다. 먼저 OLS 회귀분석으로 모형을 추정하여 통계적으로 유의하게 종속변수에 영향을 미치는 독립변수만을 포함하였다. 지역적 모형의 독립변수와 종속변수는 전역적 모형과 동일하나 추정 방법을 지리가중회귀분석으로 달리하였다. 지리가중회귀분석을 실행할 수 있는 패키지는 다양하게 있지만, 본 연구에서는 R 프로그램 패키지인 'spgwr (version 0.6-26)' (Roger Bivand, 2014)을 사용하였다. 지리가중을 위한 커널은 연구대상 표본점들의 분포를 이용하여 판단하게 되는데, 이에 대한 판단이 확실치 않을 경우, 대게 가변적 커널을 채택하게 된다. 본 연구에서도 가변적 커널을 채택하여 모형을 추정했을 때의 모형의 적합도가 더 증가하게 되었다.
전역적 모형과 국지적 모형의 적합도를 비교함으로써 행정구역별로 수집된 공간 자료의 모형 추정을 위해 더 적합한 모형을 살펴보았다.
4. 실증분석
4.1 2005년 자료 분석 결과
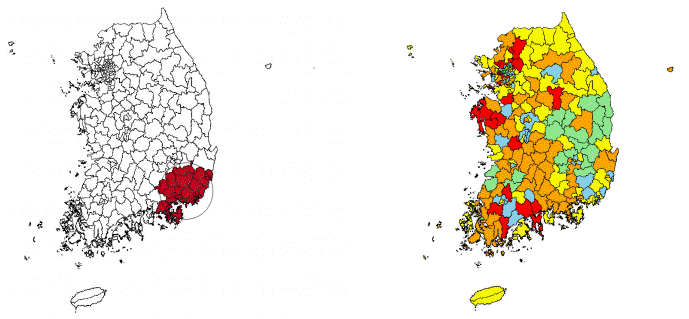
SaTScan™9.3.1을 이용하여 2005년의 순환기계통질환 사망자 수를 클러스터링 한 결과, 통계적으로 유의하게 질환에 의한 사망위험이 큰 지역을 [그림 1]의 왼쪽에 나타냈다. [Table 1]은 클러스터에 대한 정보를 보여준다.
클러스터링의 결과와 대기오염 지수의 지역적 분포에 대한 모형을 추정하기 위하여 지리가중회귀분석을 수행하고 이에 대한 결과를 Table 2에 제시하였다. 지리가중회귀분석 시, 사전에 독립변수 간 다중공선성을 검토하고 통계적으로 유의하게 영향을 주는 변수만을 고려하였다. 또한, 일반적인 OLS 회귀모형과 비교하여 지리가중회귀모형이 보다 유용한지를 평가하기 위해 동일한 독립변수를 적용하여 도출된 결과를 함께 제시하였다.Table 2를 살펴보면 2005년 순환기계통질환 사망자 수에 영향을 미치는 대기오염은 CO이다. 공간적 자기상관 결과를 살펴보면 OLS 회귀모형의 Moran I 지수는 0.262이고, 지리가중회귀모형의 Moran I 지수는 -0.056으로 지리가중회귀분석을 통해 공간적 자기상관의 문제가 해결되었음을 알 수 있다. 모형의 적합도를 살펴보면 OLS 회귀모형의 R2=0.014, AIC=2216.51이고, 지리가중회귀모형의 R2=0.709, AIC=1958.54로 OLS 회귀모형에 비해 지리가중회귀모형을 적용하였을 때의 적합도가 개선이 되었음을 알 수 있다. 총 251개의 회귀계수가 도출 되었다.
4.2 2009년 자료 분석 결과
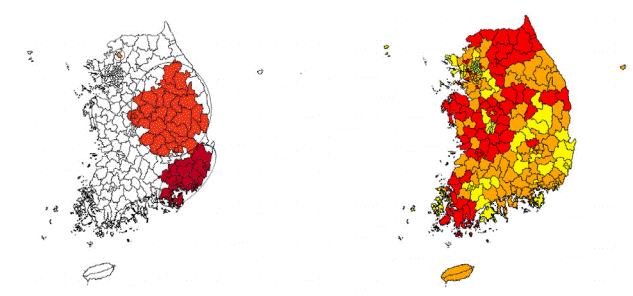
2009년의 순환기계통질환 사망자 수를 클러스터링 한 결과, 통계적으로 유의하게 질환에 의한 사망위험이 큰 지역을 Figure 2의 왼쪽에 나타냈다. Table 4는 클러스터에 대한 정보를 보여준다.
클러스터링의 결과와 대기오염 지수의 지역적 분포에 대한 모형을 추정하기 위하여 지리가중회귀분석을 수행하고 이에 대한 결과를 Table 5에 제시하였다.
Table 5를 살펴보면 2009년 순환기계통질환 사망자 수에 영향을 미치는 대기오염은 SO2, NO2, CO이다. 공간적 자기상관 결과를 살펴보면 OLS 회귀모형의 Moran I 지수는 0.183이고, 지리가중회귀모형의 Moran I 지수는 0.021로 지리가중회귀분석을 통해 공간적 자기상관의 문제가 해결되었음을 알 수 있다. 모형의 적합도를 살펴보면 OLS 회귀모형의 R2=0.141, AIC=2110.99이고, 지리가중회귀모형의 R2=0.6, AIC=1959.19로 OLS 회귀모형에 비해 지리가중회귀모형을 적용하였을 때의 적합도가 개선이 되었음을 알 수 있다.
4.3 2013년 자료 분석 결과
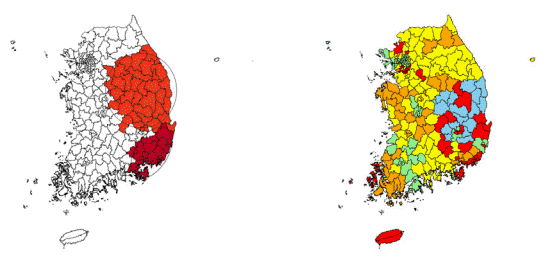
2013년의 순환기계통질환 사망자 수를 클러스터링 한 결과, 통계적으로 유의하게 질환에 의한 사망위험이 큰 지역을 [Figure 3]의 왼쪽에 나타냈다. [Table 7]은 클러스터에 대한 정보를 보여준다.
클러스터링의 결과와 대기오염 지수의 지역적 분포에 대한 모형을 추정하기 위하여 지리가중회귀분석을 수행하고 이에 대한 결과를 Table 8에 제시하였다.
Table 8를 살펴보면 2013년 순환기계통질환 사망자 수에 영향을 미치는 대기오염은 SO2, PM10, O3, NO2, CO이다. 공간적 자기상관 결과를 살펴보면 OLS 회귀모형의 Moran I 지수는 0.206이고, 지리가중회귀모형의 Moran I 지수는 -0.009로 지리가중회귀분석을 통해 공간적 자기상관의 문제가 해결되었음을 알 수 있다. 모형의 적합도를 살펴보면 OLS 회귀모형의 R2=0.249, AIC=2038.42이고, 지리가중회귀모형의 R2=0.617, AIC=1901.34로 OLS 회귀모형에 비해 지리가중회귀모형을 적용하였을 때의 적합도가 개선이 되었음을 알 수 있다. 총 251개의 회귀계수가 도출 되었다.
Figure 3의 오른쪽은 지리가중회귀모형의 회귀계수를 K-means 군집분석을 하여 지역적 분포를 나타낸 그림이다. 지역별로 대기오염 분포 특성은 [Table 9]에 제시하였다. 1번 군집은 PM10의 영향이 가장 작은 지역으로 김천, 구미, 대구광역시 일부 지역, 합천, 의령, 밀양, 신안, 제주시 등이 이에 해당한다. 2번 군집은 SO2와 O3의 영향이 가장 큰 지역으로 춘천, 인제, 양양, 충청도, 전라남도 왼쪽 지역 등이 이에 해당한다. 5번 군집은 PM10과 CO의 영향이 가장 크고, O3와 NO2의 영향이 가장 작은 지역으로 일부 지역을 제외한 경상북도가 이에 해당한다.
5. 결 론
본 연구에서는 순환기계통질환 사망자 사망자에 대한 대기오염의 영향을 알아보기 위해 대기오염의 지역별 분포와 유의한 영향을 주는 대기오염 종류를 살펴보았다. 이때, 행정구역 별로 수집된 공간 자료의 공간적 자기상관 문제를 해결하기 위해 지리가중회귀분석을 적용하였다. 순환기계통질환 사망자에 대한 지리가중회귀분석 결과는 지역 내의 위치에 따라 모형에 포함된 대기오염 변수의 영향이 차이가 있다는 것을 보여주었다. 지리가중회귀분석으로 추정한 모형이 OLS 회귀모형보다 모형의 설명력과 적합도가 개선되었음을 확인할 수 있었다. 또한, 지리가중회귀분석을 적용하여 공간적 자기상관 문제가 제거되었거나 완전히 제거되지는 못했지만 보다 개선이 된 것으로 나타났다.
연도별로 질환 사망자 수에 영향을 미치는 유의한 변수를 살펴보면 Table 10과 같다. Table 10은 연도별 순환기계통질환에 유의한 영향을 주는 대기오염 변수를 나타냈다. 순환기계통질환은 매해 CO의 영향을 받고 있다.
본 연구에서 순환기계통질환 사망자 사망자에 영향을 미치는 요인으로 대기오염 변수를 제외한 다른 요인들을 배제하여 나타나는 제한점이 있었다. 매해 발생한 대기오염과 같은 해의 질환 사망자 수를 비교하는 것이나 환자의 지역 이동사항 등에 대한 정보의 제한점이 있다. 이는 추후 연구를 통해 검토돼야 할 필요성이 있다고 본다. 또한 공간적 상관성 뿐 만 아니라 공간적 이질성을 반영하는 다른 상관구조(예, MRF(Markov-random field; Cressie, 1993) 또는 CAR(conditional autoregressive model; Besag et al., 1991)를 사용할 필요도 있을 것 같다. 이러한 제한점에도 불구하고 지리가중회귀분석의 특성을 고려해 보았을 때, 본 연구 방법론을 활용 가능할 뿐만 아니라 대한 향후 지속적인 연구를 통해 대기오염의 관리 및 질환의 예방에 근거가 될 수 있을 것으로 판단된다.